橫看成嶺側成峰
—— 一道含參根式題的多維破解

☉江蘇省南通中學 李維堅

函數最值問題是高中數學的重要問題之一，其求解方法很多.近幾年，函數解析式中含有二次根式，并求其最值的問題層出不窮.一般可采用分子（分母）有理化、平方、換元（包括三角換元，雙變量換元）、配方、導數、均值不等式、柯西不等式、數形結合、判別式法，構造法（向量法構造、幾何圖形構造）等各種方法來解決形如等含二次根式的函數.其中（fx），g（x）多以一次函數、二次函數、三角函數等形式給出.以上方法靈活解決這些函數時，無出其右.而當這類函數中含參，已知函數最值，逆向求參數范圍時，思維角度就更廣更多樣.下面就以一道高考模擬題舉一隅而反三隅.

導數的引出和定義始終聯系著函數的思想，涉及數學中多種思想方法，同時又是銜接初、高等數學的橋梁，它的出現為解決一些數學問題提供了新的視野.導數作為一種工具，在解決數學問題中有廣泛應用，而導數又是一種特殊的函數，對加深函數的理解和直觀認識有重要作用，所以在處理函數的單調性、圖像、凹凸性與拐點、極值與最值、參數等問題時作用尤為顯著.應用傳統的定義法和圖像法解決這類函數問題，雖然比較突出本質，但是若問題中函數比較復雜時，會加大解題者的壓力，而應用導數處理則有清晰的解題思路，具有解題效率高的特點.特別當面對奇怪難看的函數，只要克服運算上的畏難心理，不要畏縮不前，那么這個問題用導數這個工具還是可以化解的.

策略二、均值不等式

易知a>0，a≠1，且（fx）是定義域上的奇函數，其值域關于原點對稱，所以

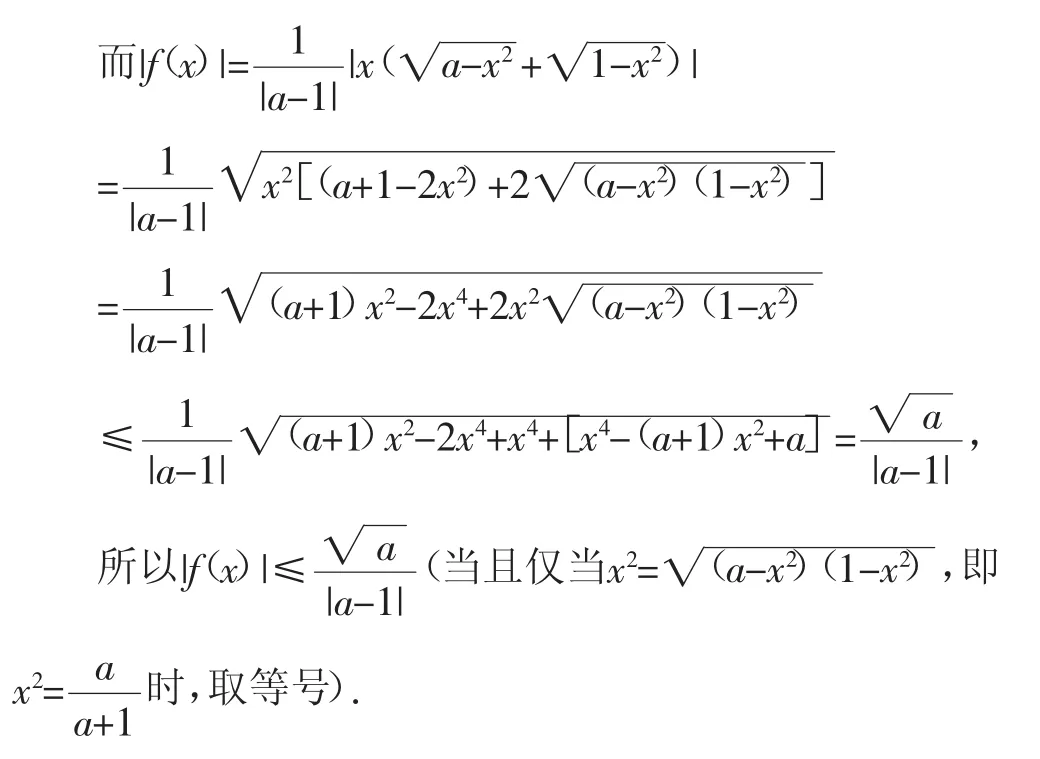
本題結合平方化方法，利用基本不等式局部處理變量的最值，起到了撥開云霧見晴天的作用.均值不等式在求最值，比較大小，逆向求參數的范圍，證明不等式等方面有廣泛的應用.解題的突破口在于如何湊出定值——積定和最小，和定積最大.

策略三、構造法之幾何圖形

設∠BAD=α，∠CAD=β.

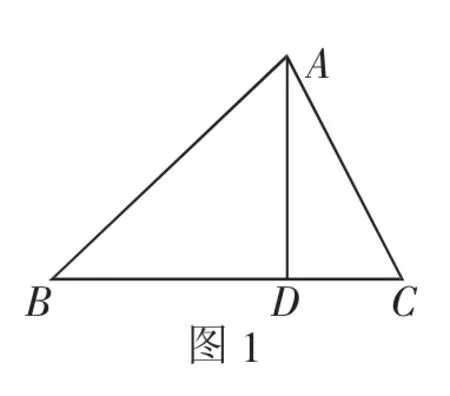
因為2S△ABC=CB·AD=AB·ACsin∠BAC≤AB·ACsin90°，所以當且僅當α，β互余，即時，取等號.

一些代數問題，用代數方法求解很麻煩，甚至一時不知從何處著手.若我們通過觀察發現問題條件的數量關系有著明顯的幾何意義或可將該問題轉化為幾何圖形，這時我們就可以借助幾何圖形的性質，從而使問題得到解決.由上面的例子我們可以看出，構造法具有很大的靈活性和技巧性，它是多種思維方式滲透、連貫、融會的產物.我們解題時不是胡思亂想瞎構造，而是依據數量關系所賦予的幾何特征而構造出不同的幾何模型的.用構造法解題有利于學生打破思維定勢，激發創造性思維，培養學生敏銳的觀察力，提高學生分析、解決問題的能力.

策略四、構造法之向量

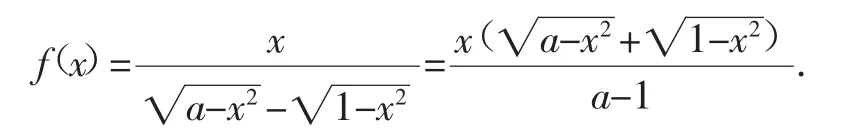
一般來說，由根式的結構形式可以聯想到距離、模長等，不難發現的結構與向量的數量積的坐標形式特別相似，且注意到與x的平方和為常數，所以考慮構造向量來解題.當然向量的|m·n|≤|m||n|這個不等式其實是柯西不等式的二維形式，所以本題直接用柯西不等式也是一樣的.

當遇到一些比較抽象的題目，一時難以下筆時，不妨考慮一下它能否在已學習的具象化概念或者我們的生活中找到原型，將問題放到我們構造的熟悉的數學模型或者實際環境中去研究，化抽象為具體，化復雜為簡單，從而達到解題的最終目的.

“構造法”是指為解決某個數學，利用知識間內在聯系或是形式上的某種相似性，先構造一種數學形式（比如幾何圖形、代數式），尋求與問題的某種內在聯系，使之簡單明了，起到簡化、轉化和橋梁的作用，從而找到解決問題的思路與方法.它重在“構造”，深刻分析、正確思維和豐富聯想，它體現了發現、類比、化歸等思想，滲透著猜想、試驗、探索、概括等重要方法，是一種富有創造力的解決問題的方法.

策略五、化歸為二次函數的判別式法

某些極端情況下可將函數的最值問題轉化為恒成立問題，通過一步步變形，可以采用分離參數的方法或者當參變糾纏不清時，轉化為二次函數的恒成立問題，利用判別式法逆向問題正向求解，對于本題而言，思維含量不大，但是有一定的計算量.

判別式法求函數的值域是易于理解的，但是當題目中x的限制條件太多時，會陷入復雜的分類討論中.但是這種比較初等的方法在解決一些填空題的怪題時雖略顯簡單粗暴但確實有奇效.

多角度解題是開發智力、培養能力的一種行之有效的方法，它對溝通不同知識間的聯系，開拓思路，培養發散思維能力，激發學生的學習興趣都十分有益.在教學中，恰當而又適量的采用一題多解的方法，進行思路分析，探討解題規律和對習題的多角度追蹤，能以少勝多的鞏固基礎知識，提高分析問題和解決問題的能力，掌握基本的解題方法和技巧，提升學生的數學素養和數學精神.