函數值域的求法分類例析

☉山西省呂梁市賀昌中學 高永亮

高中數學中，函數部分是重點也是難點，其中求函數的值域（求函數的最大、最小值）尤為重要.在這里筆者做了一個相對系統的整理，供廣大高中數學教師與學生在學習過程中參考與使用.

一、直接法

例1求函數（fx）=的值域.

解析：由3x+1∈（1，+∞），得（fx）=故函數（fx）=的值域為（1，3）.

二、配方法

例2已知函數（fx）=x2-4x+1，x∈［-2，5］，求函數y=（fx）的值域.

解析：由（fx）=x2-4x+1=（x-2）2-3，

故當x=2時，ymin=-3；當x=-2時，ymax=13.

因此函數（fx）=x2-4x+1，x∈［-2，5］的值域為［-3，13］.

說明：在高中，二次函數y=ax2+bx+c（a≠0）在求其值域等其他問題時，一般采用配方將其化為形如再通過二次函數的性質，求其值域或解答相關問題.

三、判別式法

例3求函數的值域.

解析：由得函數的定義域為R，原式可化為：（y-1）x2+（1-y）x+y=0，當y=1時，x∈?.

當y≠1時，又x∈R，我們把上式看成關于x的一元二次方程，得Δ=（1-y）2-4y（y-1）≥0，解得

說明：此類型的分式函數，特別是定義域為R的分式函數，通常將其變形得到形如關于x的二次函數，再采用判別式大于等于零求函數的值域是一種很好的方法.

四、分離常數法

因此原函數的值域為{y|y≠1}.

說明：此類型的函數，分子、分母都含有自變量，而通過分離常數法，可以將此類函數的變量只含到分母上，分子化為常數，使函數值y的范圍變化容易確定，從而較為簡單地求出函數的值域.

五、換元法

例5求函數的值域.

解析：設從而得（fx）=g顯然函數g（t）在［0，+∞）上為單調遞減函數，所以g（t）≤g（0），因此原函數的值域為

說明：若所求函數是含有根式結構的函數，通常采用換元法，通過變形將無理式化為我們熟悉的有理式，再進一步求出函數的值域（.事實上，從本質而言，這類函數就是二次函數）

六、利用函數的單調性

例6求函數的值域.

解析：易得函數的定義域為

說明：通過判定函數的單調性，再求函數的值域，能做到事半功倍.利用函數的單調性，求函數的值域是一種重要方法.對于本類題型，也可使用題型5的解法.

七、圖像法

例7 求函數y=|x-1|+|x+3|的值域.

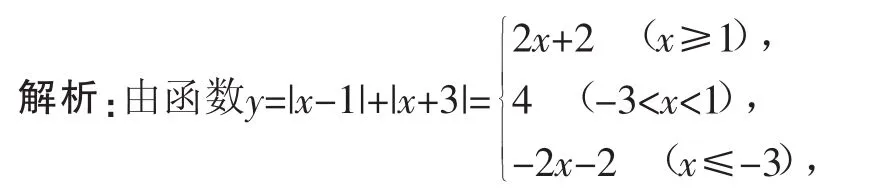
作出其簡圖（圖略），通過圖形易得函數y=|x-1|+|x+3|的值域為［4，+∞）.

八、利用幾何意義法

例8求函數y=|x-1|+|x+5|的值域.

解析：由絕對值的幾何意義，式子|x-1|+|x+5|表示數軸上任一數x對應點P到數1與數-5對應兩點A、B的距離之和，在數軸上容易得到線段AB上的點到此二點距離之和最小為6，其他點到此二點距離之和恒大于6，因此函數y=|x-1|+|x+5|的值域為［6，+∞）.

說明：在數軸上|x|的幾何意義是：數軸上任一數x對應點P到原點的距離；在數軸上|x-a|的幾何意義是，數軸上任一數x對應點P到數a對應點A的距離，即|PA|之長.

九、利用公式|a|-|b|≤|a±b|≤|a|+|b|

例9求函數y=|x-1|+|x+5|的值域.

解析：由公式得y=|x-1|+|x+5|≥|（x-1）-（x+5）|=6.

因此函數y=|x-1|+|x+5|的值域為［6，+∞）.

說明：不等式|a|-|b|≤|a±b|≤|a|+|b|，是求最大、最小值與證明不等式的常用公式之一，如果能靈活應用，問題的解答就特別簡單了.

十、利用基本不等式

基本不等式是高中數學中求最大與最小值（求值域）常用的一種基本方法之一，在使用中要求關系式滿足：一正、二定、三相等的條件.

十一、三角換元法

基本不等式、三角函數、二次函數、求導是高中數學中求最大與最小值（求值域）最常用的四種方法.三角函數是通過利用正弦函數與余弦函數的有界性，即|sinx|≤1，|cosx|≤1，從而解答有關三角函數問題的最大與最小問題，本類問題的關鍵是通過合理的三角換元把函數最值問題轉化為三角函數問題，進一步求出所求函數的值域.

十二、利用定義域求值域

例10求函數的值域.

解析：由函數得ex-e-x≠0，易得函數的定義域為{x|x≠0}.

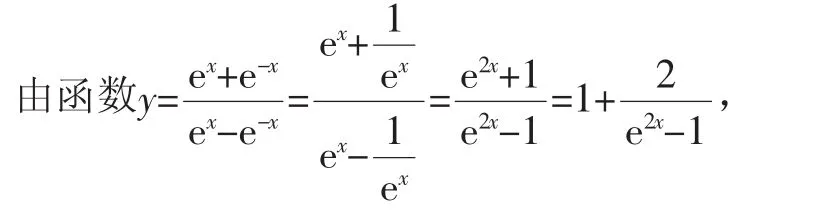
說明：先求出函數的定義域，再通過變形把含自變量x的式子移到一邊，把含y的式子移到一邊，再通過函數的定義域直接轉化為關于y的式子的范圍，進一步求出y的取值范圍，即求出函數的值域.這種方法，理論上是總成立的，它采用數學中的轉化思想，把函數的定義域轉化到函數的值域.只不過有的時候這種轉化甚為麻煩，我們根據實際情況，合理使用，不要過于死板.

十三、求導求值域

說明：通過求導是求函數值域（最大值與最小值）的通用方法，從理論而言，一般函數的值域都可以用求函數的導數解答，不過有時求導去解答比較麻煩，用上面的一些方法更為簡單.

上面對求函數值域（最大值與最小值）問題的探索，不足之處，望廣大師生批評指正.