關注數學活動經驗 提升學生思維能力
—— 以一節橢圓性質探究課為例

☉江蘇省啟東中學 胡 勇

一、引言

基本活動經驗是數學課程標準中提出的“四基”之一，也是近年來教育教學研究的熱點，相關的研究論文很多.在眾多研究結果中，對數學活動經驗的認識和理解還存在著一定程度的差異，但在以下兩個方面卻基本上保持一致.

一是對數學活動經驗的價值認同，即“數學活動的過程不僅能夠加深學生對數學概念、性質、定理的理解，同時數學活動經驗的積累也是形成學生創新能力的基礎.”

二是對數學活動經驗的形成機制，即“學生的數學活動經驗是在做數學的過程中形成的，它的產生和形成實質上是學生經歷數學活動的過程.”

下面以筆者近期在本校開設的一節市級公開課為例，談談對促進學生數學活動經驗積累的探索和思考.

二、基本情況分析

1.教學內容分析

直線與橢圓的位置關系是學生學習的難點之一，主要表現在：對問題的本質理解模糊，只知“埋頭運算”，不知“抬頭識路”，缺乏解題策略的選擇意識，往往因為方法不合理而半途擱淺，或因計算過于煩瑣而產生厭煩、畏懼心理.針對學生這一普遍存在的困惑，在復習橢圓及其性質后設計本節探究內容，讓學生在自主探究的過程中體會解決解幾問題的一般策略和方法.

2.教學目標

（2）通過探究橢圓的性質，理解直線與橢圓問題解決一般策略和方法；

（3）了解類比在數學發現、創新過程中的作用，領略數學發現的一般過程和快樂.

3.教學重難點

類比圓的性質得出橢圓的相關結論.

三、教學實錄

1.情境引入

師：著名天文學家開普勒曾說過：“我珍視類比勝過任何東西，它是我最可信的老師，它能揭示自然界的秘密，在幾何學中，它應該說是最不能忽視的.”開普勒如此推崇類比，可見它在自然科學更多是在數學發展中的重要地位.今天，就讓我們一起來運用這一有力武器，探究并發現橢圓中的一些結論.

點評：用偉大科學家的話激發學生學習的興趣.開場白直接點明類比思想，為接下來的發現之旅指明方向.

2.自主探究，意義建構

探究問題1：如圖1，已知圓O：x2+y2=r（2r>0）上兩點M，N，且OM⊥ON.在此條件下你能得出哪些結論？類比到橢圓中，你能得出哪些猜想？

學生分組討論、交流，教師巡視.大約5分鐘后由小組指派代表發言.

圖1

圖2

生2（另一小組成員）：錯了！兩直線垂直的條件也要改.

師：怎么改？為什么？

學生獨立探究，教師對學習困難的同學進行點撥，大約10分鐘后學生展示成果.

生3：猜想成立，證明如下：

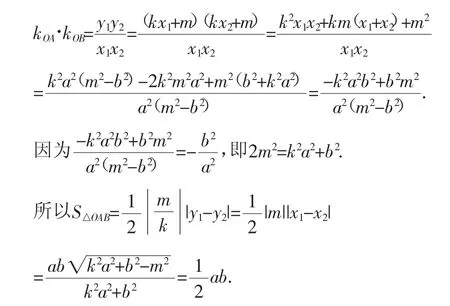
故猜想成立.

師：很好.除了上述猜想，同學們還有別的猜想嗎？

生4：類比圓中結論OM2+ON2=2r2有OA2+OB2=a2+b2.利用上述證明可得：

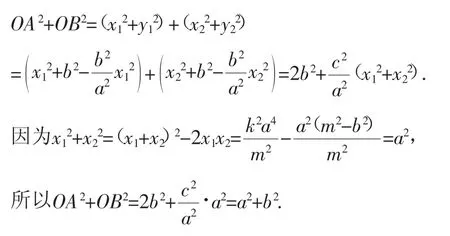
生5：類比圓中弦中點的軌跡還是圓，猜想橢圓中弦AB的中點P的軌跡仍是橢圓.

所以線段AB的中點P的軌跡是橢圓，

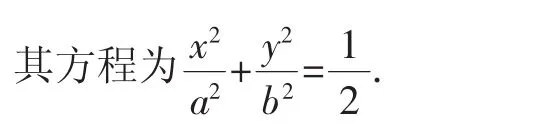
探究問題2：想一想圓中與兩直線垂直的有關結論，它們可以類比到橢圓中嗎？

學生分組探討、交流，教師參與討論，適時點撥.大約10分鐘后由各組指派同學展示探究成果.

生6：類比“圓中直徑所對圓周角是直角”得到：如圖3，已知點A，B，P在橢圓上，若直線PA，PB的斜率存在，則A，B關于原點對稱

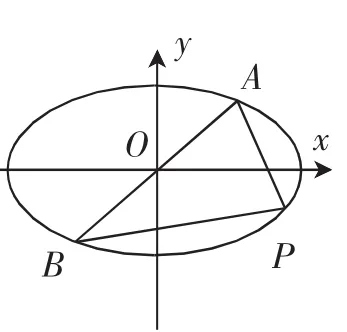
圖3

生7：類比“圓中平分弦（不是直徑）的直徑垂直于弦”得到：如圖4，已知與坐標軸不垂直的直線l與橢圓交于點A，B，線段AB的中點為M，則

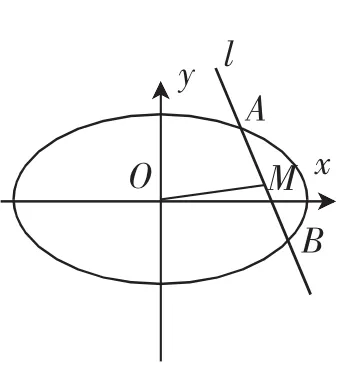
圖4

證明如下：設M（x0，y0），則

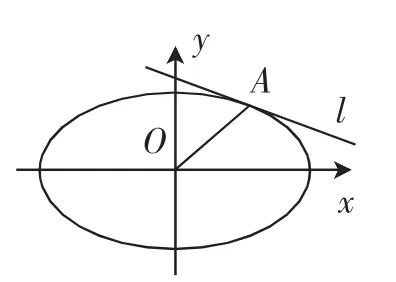
圖5

點評：從探究的空間、時間、層次等方面為學生營造了一個較為寬松的探究情境，使得整個探究過程基本上自成體系、有序、環環相扣，各個探究過程之間密切相關，做到由淺入深、由易到難、由現象到本質.

師：請同學們總結一下，我們得到哪些結論.

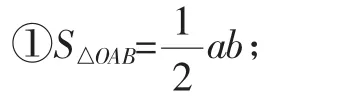
②OA2+OB2=a2+b2；

點評：數學知識是可以直接授受的，但數學活動經驗卻不能傳遞，只有學生親身經歷自主探究，完整經歷數學家發現數學結論的一般過程，才能夠切身體會知識發生發展的過程，提高運算求解和思維能力，體驗學科研究的一般方法，積累活動經驗.

3.反思總結，凸顯本質

（1）本節課得到了橢圓的哪些性質？

（2）本節課在證明橢圓有關性質時運用了哪些方法？

（3）本節課得到橢圓性質的過程，遵循了怎樣的研究方法和一般過程？

點評：讓學生反思經歷的數學活動，回顧基本知識、技能，感悟科學研究的一般方法和過程，使得學生所獲得數學活動經驗由“懵懂模糊”逐漸“清晰明確”，重新建構認知體系.

四、數學活動的幾點認識

1.數學活動開展立足于教師的精心預設

成功的課堂教學離不開預設，只有精彩的預設，才能和諧生成.設計什么樣的數學活動才能真正提升學生的數學活動經驗呢？

首先，要對學生原有認知結構中的數學活動經驗進行分析與聯結.數學學習的類似性使得儲存在學生頭腦中的數學活動經驗具有很強的遷移性和認同性，因此在分析數學知識、數學技能、數學學習心理特征時，還應將學生數學活動經驗分析納入學情分析的范圍.

其次，結合學情和教學內容確定數學活動經驗積累的具體、可行的目標.目標解析采用條目式，以求簡潔、準確表達“理解”、“掌握”的具體內容.

最后，合理設計數學活動的各個環節.活動的進程設計除了觀察、實驗、操作、探討和交流等操作層面外，更要注重數學活動背后蘊涵的數學思維活動，“數學活動經驗的核心應是數學思維活動經驗.”

2.數學活動經驗生成于學生的自主探究

數學活動經驗是動作和心智交互作用的結果.學生是學習的主體，教師要注意角色定位的轉換，由傳統的知識傳授者轉向現代的學生發展的促進者.教師的角色應定位在組織指導者、合作交流者，課堂是復雜的，運動變化的，由于多種不確定因素的存在和相互作用，“預設”不可能窮盡課堂所有可能的變化.當學生遇到這樣那樣的挫折和失敗需要得到幫助時，教師應該鼓勵、引導.

3.數學活動經驗提升于學生的反思悟透

弗萊登爾說過：“反思是數學思維活動的核心和動力，沒有反思，學生的理解就不可能從一個水平升華到更高的水平”.學生在經歷數學活動后，所形成的數學活動經驗是懵懂模糊的，只有對數學知識形成過程中體現的研究方法和研究經驗進行適當的總結和反思，才能進行合理的知識建構，才能提高自己的思維能力，才能使所獲得的數學活動經驗更加清晰明確.教師作為教學的主導者、幫助者、引導者，一定要有反思的意識和習慣，要多在反思體驗處構建數學活動經驗，以促進學生認知結構的發展.