高中數(shù)學(xué)“同類知識(shí)”的自主學(xué)習(xí)策略研究

☉江蘇省西亭高級(jí)中學(xué) 黃素霞

圓錐曲線、立體幾何、函數(shù)、數(shù)列中都包含很多的同類知識(shí)，教師如果能夠站在較高的角度對(duì)這些同類知識(shí)進(jìn)行教學(xué)往往能夠培養(yǎng)學(xué)生終身自主學(xué)習(xí)的能力，本文結(jié)合學(xué)生自主學(xué)習(xí)能力的培養(yǎng)對(duì)橢圓教學(xué)淺談自己的一點(diǎn)感悟.

橢圓、雙曲線、拋物線是運(yùn)用平面對(duì)圓錐面進(jìn)行三種不同截法而產(chǎn)生的不同曲線.事實(shí)上，圓錐曲線是動(dòng)點(diǎn)在不同約束條件下運(yùn)動(dòng)所形成的軌跡.本文結(jié)合橢圓教學(xué)所進(jìn)行的思考是基于學(xué)生橢圓知識(shí)的掌握，更為重要的是幫助學(xué)生在橢圓的學(xué)習(xí)中掌握雙曲線、拋物線以及一般曲線的方法，并因此達(dá)成“授人以魚，不如授人以漁”的教學(xué)宗旨.

一、何謂定義

1.下定義的緣由與方法

當(dāng)人們?cè)诳茖W(xué)研究中發(fā)現(xiàn)某個(gè)重要且值得研究的對(duì)象時(shí)往往會(huì)對(duì)其本質(zhì)屬性進(jìn)行挖掘并給出其定義，否則就會(huì)產(chǎn)生目標(biāo)不明確的混亂局面.

何謂定義呢？人們?cè)诖_定認(rèn)識(shí)對(duì)象或事物在一定綜合分類系統(tǒng)中所運(yùn)用的判斷或命題式的語(yǔ)言邏輯形式就是我們通常所說的定義，定義可以說是某種事物在一定范疇內(nèi)的界限與具體位置.人們對(duì)某一種事物的本質(zhì)特征或概念內(nèi)涵、外延所作出的確切表述是數(shù)學(xué)角度上關(guān)于定義的解釋.由此可見，對(duì)不同對(duì)象進(jìn)行研究時(shí)首先應(yīng)做的便是對(duì)該對(duì)象下定義，定義一般具有作為判斷與性質(zhì)的雙重性特征.

學(xué)生明確下定義的緣由與方法之后，自然也就更加明白學(xué)習(xí)新知識(shí)時(shí)對(duì)研究對(duì)象下定義的必要性與重要性，也對(duì)所學(xué)定義在解題以及新知識(shí)學(xué)習(xí)中的應(yīng)用價(jià)值產(chǎn)生更深刻的理解.

2.定義的等價(jià)形式

橢圓定義：平面內(nèi)到兩定點(diǎn)F1、F2的距離之和等于常數(shù)（大于F1F2）的點(diǎn)的軌跡叫橢圓，F(xiàn)1、F2兩個(gè)定點(diǎn)叫作橢圓的焦點(diǎn)，兩焦點(diǎn)之間的距離叫作橢圓的焦距.

例1已知△ABC中，B（-3，0）、C（3，0），且AB、BC、AC成等差數(shù)，則頂點(diǎn)A在什么樣的曲線上運(yùn)動(dòng)呢？（橢圓）

例2如圖1，與圓F1外切并與圓F2內(nèi)切的圓的圓心C在什么樣的曲線上運(yùn)動(dòng)？（橢圓）

雖說研究對(duì)象在一般情況下只有一個(gè)基本定義，但描述研究對(duì)象的相同屬性之時(shí)因?yàn)榻嵌鹊牟煌鶗?huì)產(chǎn)生定義條件下的多個(gè)等價(jià)形式，學(xué)生明白這一道理也就能夠理解各種不同條件下都能得到相同橢圓的原因了，不僅如此，學(xué)生在后續(xù)圓錐曲線的學(xué)習(xí)中還會(huì)更加容易獲得正確的理解與感悟，學(xué)生在自主學(xué)習(xí)中也會(huì)因此掌握研究平面曲線的方法并為解析幾何的學(xué)習(xí)奠定基礎(chǔ).

那么，教師在橢圓的定義得到明確之后應(yīng)該如何引導(dǎo)學(xué)生進(jìn)行進(jìn)一步的探究呢？

師：圓的定義是我們同學(xué)在初中階段就學(xué)習(xí)過的，那么我們對(duì)圓的性質(zhì)是怎樣進(jìn)行進(jìn)一步研究的呢？

生：運(yùn)用圓的方程.

師：為什么呢？

這一問題的提出事實(shí)上是解析幾何本質(zhì)問題的涉及：將幾何問題進(jìn)行以數(shù)定形、以形定數(shù)，也就是通常所說的幾何問題數(shù)量化，并在此過程中實(shí)現(xiàn)完美的數(shù)形結(jié)合并最終獲得研究真實(shí)圖形的方法.

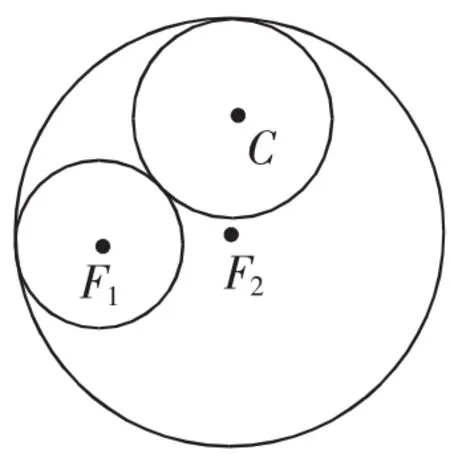
圖1

二、研究對(duì)象的方程

師：圓的方程的建立大家是否還記得呢？

學(xué)生回答教師提出的這一問題，教師進(jìn)行適當(dāng)引導(dǎo)并最終得出建坐標(biāo)系、設(shè)點(diǎn)、列等式、代坐標(biāo)、化簡(jiǎn)這一建立圓的標(biāo)準(zhǔn)方程的步驟.

師：這一方法會(huì)不會(huì)一樣適用于橢圓呢？

生：適合.

運(yùn)用建立圓的方程的步驟將求橢圓方程的五大基本步驟自然引出，伴隨這一過程的探索，教師對(duì)其中兩個(gè)步驟可以進(jìn)行著重說明.

（1）應(yīng)該怎樣建立適當(dāng)?shù)淖鴺?biāo)系？

針對(duì)同一個(gè)橢圓選擇不同的直角坐標(biāo)系所推出的相應(yīng)方程式往往是不一樣的，一般表現(xiàn)在焦點(diǎn)分別在x軸、y軸的標(biāo)準(zhǔn)方程上.因此，此時(shí)坐標(biāo)系的建立應(yīng)盡量使方程的形式與運(yùn)算簡(jiǎn)單，這是一種同樣適合研究其他曲線、曲面及幾何體的方法.

（2）如何列等式？

將橢圓上的動(dòng)點(diǎn)所受的幾何約束轉(zhuǎn)化成代數(shù)形式是最為根本的環(huán)節(jié)，根據(jù)條件可得：

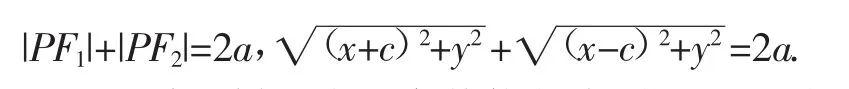
這是一種同樣適合研究其他曲線、曲面及幾何體的方法.

三、研究對(duì)象的圖形

師：研究橢圓方程會(huì)有什么好處呢？

生：可以根據(jù)方程畫出圖像并進(jìn)行其性質(zhì)的研究.

師：很好.根據(jù)橢圓方程畫出圖形更加便于我們對(duì)其形態(tài)進(jìn)行觀察，進(jìn)一步研究其性質(zhì)也會(huì)變得更加容易，這是一種同樣適合研究其他曲線、曲面及幾何體的方法.

四、研究對(duì)象的性質(zhì)

橢圓的幾何性質(zhì)應(yīng)該怎樣研究呢？（學(xué)生討論）

（1）首先應(yīng)該弄清楚曲線的哪些性質(zhì)需要研究，圖形的對(duì)稱性、范圍、離心率、頂點(diǎn)、漸近線等曲線上的動(dòng)點(diǎn)所具備的主要共性是曲線需要研究的性質(zhì)，需要特別注意的是不同對(duì)象的幾何性質(zhì)也是有所差別的.

（2）借“數(shù)”研“形”，這是研究解析幾何、解決解析幾何題目最為關(guān)鍵且根本的方法.比如獲得曲線的直觀圖形時(shí)可以采取描點(diǎn)法；比如描點(diǎn)作圖得到橢圓并對(duì)其幾何性質(zhì)進(jìn)行觀察；比如根據(jù)方程對(duì)其幾何性質(zhì)進(jìn)行研究.一般來說，具體性質(zhì)如下：

1.范圍

同理可得|y|≤b.

由此可說明橢圓位于直線x±a與y±b所圍成的矩形內(nèi).

2.對(duì)稱性

如圖2，根據(jù)圖形可得：橢圓關(guān)于x軸、y軸、原點(diǎn)對(duì)稱.

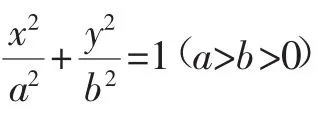
從方程上來看：

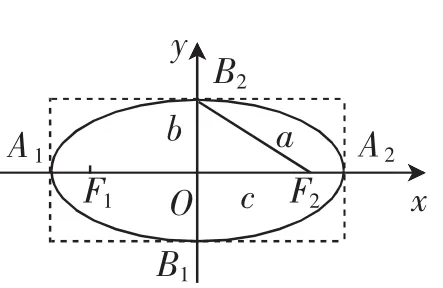
圖2

（1）將x換成-x時(shí)方程不變，說明當(dāng)點(diǎn)P（x，y）在橢圓上時(shí)，點(diǎn)P關(guān)于y軸的對(duì)稱點(diǎn)P′（-x，y）也在橢圓上，因此橢圓的圖像關(guān)于y軸對(duì)稱；

（2）將y換成-y時(shí)方程不變，因此橢圓的圖像關(guān)于x軸對(duì)稱；

（3）將x換成-x并同時(shí)將y換成-y時(shí)方程不變，因此橢圓的圖像關(guān)于原點(diǎn)成中心對(duì)稱.

綜上所述，橢圓的對(duì)稱軸與對(duì)稱中心分別是坐標(biāo)軸和原點(diǎn)，其對(duì)稱中心也叫作橢圓的中心.

3.頂點(diǎn)

4.離心率

離心率：橢圓的焦距和長(zhǎng)軸長(zhǎng)之間的比e=c叫作橢a圓的離心率.

說明：

（1）因?yàn)閍＞c＞0，因此0＜e＜1.

（3）當(dāng)且僅當(dāng)a=b時(shí)，c=0，此時(shí)兩焦點(diǎn)重合且圖形變成為圓.

這是一種同樣適合研究其他曲線、曲面及幾何體的方法.

五、研究對(duì)象的運(yùn)用

事實(shí)上，圓錐曲線等曲線在我們的實(shí)際生活中都有著極為重要的應(yīng)用價(jià)值與理論研究?jī)r(jià)值.比如，油罐車的截面、衛(wèi)星的軌跡等都是橢圓；拋物線的性質(zhì)、雙曲線的定位點(diǎn)等可以運(yùn)用在探照燈的設(shè)計(jì)與運(yùn)用上等.由此可見，曲線研究基礎(chǔ)上的應(yīng)用是我們學(xué)習(xí)曲線的真正意義之所在.

總之，使學(xué)生掌握橢圓的知識(shí)是橢圓教學(xué)的一個(gè)重要目標(biāo)，但除此以外，教師還應(yīng)使學(xué)生能夠掌握其他曲線、曲面及幾何體的研究方法，并使其能夠進(jìn)行所學(xué)知識(shí)的運(yùn)用，這對(duì)于學(xué)生來講才是更為重要的，學(xué)生在學(xué)習(xí)過程中形成的自主學(xué)習(xí)能力與應(yīng)用能力往往能令其受益一生.