不確定隨機網絡Top-k最近節點查詢算法

連春月，李孝忠，牛浩浩

(天津科技大學計算機科學與信息工程學院，天津 300457)

實際生活中，會遇到許多非確定的現象．為了研究這類非確定的現象，17世紀誕生了概率論．概率論基于大量的歷史數據，有效解決了很多統計問題．但是，有時因為各種原因無法獲得足夠多的數據，這時使用概率論解決問題就很難辦到．為了解決這類問題，Liu B于2007年提出了不確定理論[1]，并于2010年對不確定理論進行重新定義[2]，為小樣本數據、甚至是無樣本數據的統計提供了新的理論基礎．

經過多年研究與實踐，不確定理論得到了充分的發展與廣泛的應用．2013年，高原[3]詳細研究了不確定網絡的最短路徑問題；2014年，Zhou等[4]研究了不確定網絡的最短路徑的逆不確定分布問題；2015年，Zhou等[5]給出了不確定網絡的最小生成樹的路徑最優條件．

對于一個復雜網絡，某些弧的權重可以通過對歷史數據進行統計分析得到，而某些弧由于沒有歷史數據或者歷史數據無效，導致其權重不能通過概率統計得到，只能利用專家的經驗數據，得到不確定弧的權重的不確定分布函數．

2013年，為了解決這類既有非確定因素，又有不確定因素的現象，Liu Y[6]開創了機會理論．2014年，Liu B[7]首次將機會理論引入不確定網絡，提出不確定隨機網絡的概念．2015年，盛玉紅[8]對不確定隨機網絡的最短路徑問題、最小生成樹問題和最大流問題進行研究，提出理想機會分布函數的概念并利用其求解了上述問題．

關于非確定性數據的Top-k查詢問題，學者們提出了各種計算方法，包括U-topK[9]、U-kRanks[10]，PT-k[11]，Global-topK[12]等．Li 等[13]提出了基于權值參數的排名函數，實現了排名分值與概率平衡．2016年，郭長友等[14]首次將不確定理論應用到不確定數據的Top-k查詢計算中．

非確定數據的 Top-k查詢在 P2P系統、電纜鋪設等方面已經有了實際應用，但不確定數據和隨機數據同時存在的Top-k查詢方面的研究并不多．本文基于現有研究成果，將包含不確定數據和隨機數據的問題轉化為不確定隨機網絡，并在深度優先遍歷的算法上，提出在一定機會測度的情況下，尋找距離某個節點最近的k個節點的算法，能有效解決在經驗數據和小樣本數據混雜情況下的節點查詢問題．

1 相關概念

1.1 不確定理論[1]

定義1設Γ為非空集合，L是Γ上的σ-代數，任意的Λ∈L稱為一個事件．如果從L到實數集R的集函數M滿足以下條件：

公理 1(規范性) 對于全集Γ，有M{Γ}=1；

公理 2(對偶性) 對于任意的事件Λ∈L，有M{Λ}+M{Λc}=1；

公理 3(次可列可加性) 對于可數的事件序列M{Λ}，有

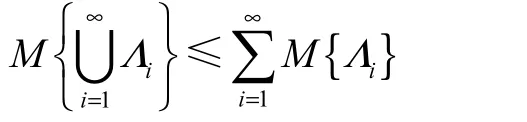
則稱集函數 M 為Γ上的不確定測度，三元組(Γ,L, M)稱為一個不確定空間．

為了研究乘積空間上的不確定測度，Liu B提出了乘積公理[1]：

公理 4設(Γi,Li,Mi)為一列不確定空間，則乘積不確定測度M為

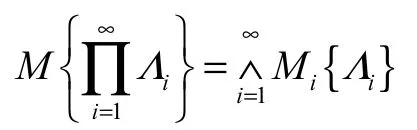
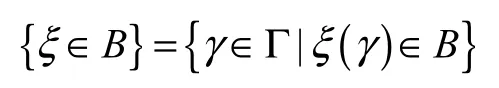
不確定變量的定義是由抽象的不確定空間和Borel集描述的．如果僅從定義出發，在理解和應用不確定變量時都會遇到困難，為了更好地理解不確定變量，給出如下不確定分布的概念．

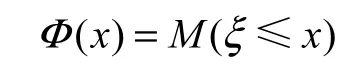
定義 4若不確定變量ξ具有不確定分布

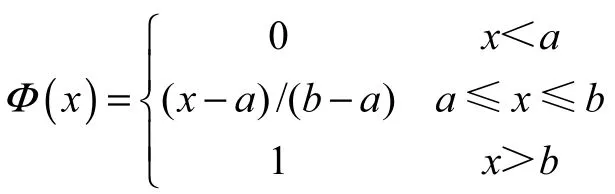
其中 a和 b為常數，則ξ為線性的不確定變量，記為L( a, b)．

定義 5若對于任意的 α∈ (0,1)，不確定變量ξ的不確定分布Φ(x)的反函數 Φ-1(α)存在且唯一，則稱Φ(x)為正則分布，稱ξ為正則不確定變量．

定義 6若不確定變量ξ具有正則分布Φ(x)，則其反函數Φ-1(α)稱為ξ的逆不確定分布．

例 1根據定義 4—定義 6，線性不確定變量L( a, b)的逆不確定分布為

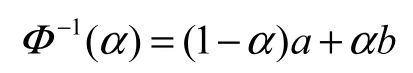
1.2 機會理論[6]

定義 7設(Γ,L,M)× (Ω,A, Pr)是一個機會空間，Θ是L×A的一個事件，那么事件Θ的機會測度為

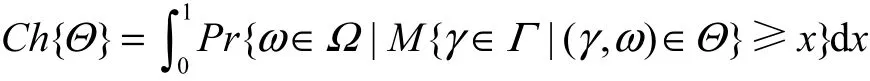
定義 8從機會空間(Γ ,L ,M )× (Ω,A, Pr)到實數集 R的可測函數ξ稱為不確定隨機變量，即對于任意的Borel實數集Β，集合

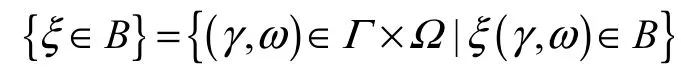
是L×A中的一個事件．定義 9設 f:Rn→R是一個可測函數，ξ1,ξ2,…,ξn是機會空間(Γ,L,M)×(Ω,A, Pr)上的一列不確定隨機變量，那么對任意的(γ,ω)∈Γ×Ω，ξ=f(ξ1,ξ2,…,ξn)是由

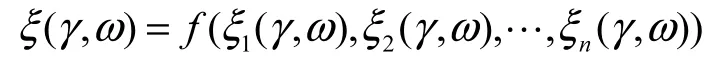
所確定的一個不確定隨機變量．

定義10η1,η2,…,ηm是一系列獨立的隨機變量，概率分布分別為Ψ1,Ψ2,…,Ψm，τ1,τ2,…,τn是一列不確定變量，不確定分布分別為?1,?2,… ,?n，那么不確定隨機變量

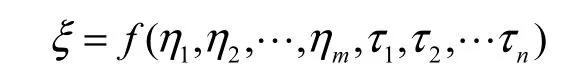
有一個機會分布

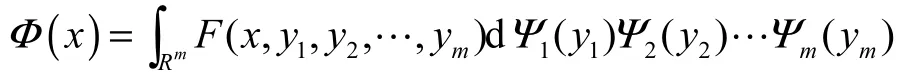
其中，對任意的實數y1, y2,…,ym，F(x, y1,y2,…,ym)是不確定變量f(η1,η2,…,ηm,τ1,τ2,…τn)的不確定分布，它可由其反函數F-1(α;y, y,…,y)=f(y,y,…,12m12y,?-1(α) ,?-1(α),…,?-1(α))決定，條件是f為對于m12nτ1,τ2,…,τn的單增函數．

例 2設η是一個隨機變量，其概率分布為Ψ，τ是一個不確定變量，其不確定分布為?．那么，ξ= η+ τ是一個不確定隨機變量，ξ的機會分布為

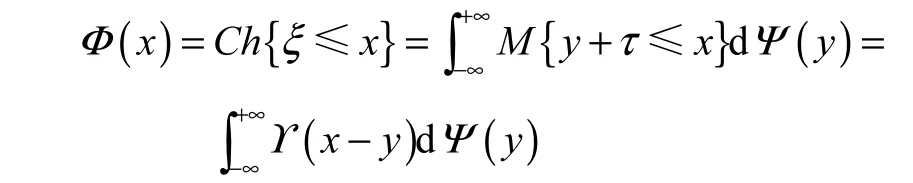
其中，y是隨機變量η的任一實現．

2 不確定隨機網絡下的Top-k查詢算法

2.1 不確定隨機網絡

N是節點集合，U是不確定弧的集合，R是隨機弧的集合，W 是不確定權重和隨機權重的集合，那么四元組(N，U，R，W)被稱為一個不確定隨機網絡．

例3圖1是有4個節點的不確定隨機網絡．其中，隨機權重ηAB、ηCD的概率分布分別為ΨAB、ΨCD．不確定權重τBC具有正則的不確定分布?BC．各邊的權重的分布函數見表1．

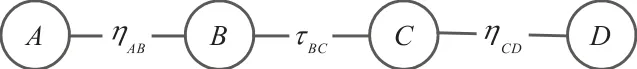
圖1 4節點不確定隨機網絡Fig. 1 Uncertain random network with 4 nodes

表1 圖1網絡中各邊的權重的分布函數Tab. 1 Distribution function of the edge’s weight of figure 1

ΨAB，ΨCD的概率分布函數分別為

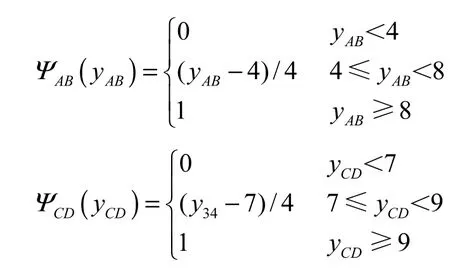
?BC的不確定分布為

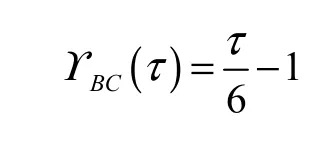
則權重的機會分布函數為

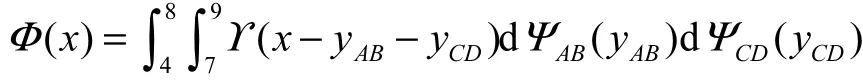
計算可得

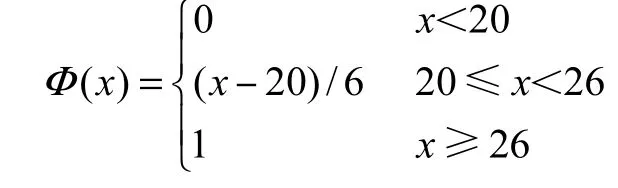
假設機會測度Φ (x) =0.95，計算得權重x=25.7．

2.2 Top-k最近節點查詢算法

給定不確定隨機網絡G，節點間的權重的機會分布函數為Φ，則節點間的路徑長度機會分布函數D＝Φ，即將節點間的權重建模為節點間的路徑長度．基于節點間的路徑長度，提出以下的不確定隨機網絡Top-k最近節點查詢算法．

輸入：不確定隨機網絡 G＝(N，U，R，W)，選擇的最近節點個數k，初始節點p，機會測度α．

輸出：當機會測度為α時，與 p最近的k個節點，以及對應路徑．

具體算法如下：

(1)計算所有節點間 i，j間的路徑，初始節點為：i＝1，j＝2，并將 i標記為已訪問；

(2)從N中取出非i節點k，若兩點間有路徑，將k標記為已訪問；

(3)若k＝j，將所有已訪問節點組成的路徑放入路徑集合D中，回溯至上一個已訪問節點，重復步驟(2)；否則，重復步驟(2)；

(4)若 k≥n，j++，重復步驟(1)—(3)，直至 j＝n；

(5)若 j＞n，j- -，i++，重復步驟(1)—(4)，直至 i＝n；

(6)計算D中所有路徑的機會分布函數；

(7)計算當機會測度為α時，點 p到所有節點的路徑長度；

(8)找到距離點 p最近的k個點及對應路徑，算法結束．

算法中步驟(2)—(3)部分的代碼如下：

function FindPath(matrix，startNode，endNode){

result[nPos]＝startNode.key；//將當前節點放入結果集

Mark[startNode.key]＝true；//標記為已訪問nPos++；

while(nPos !＝0){

var tempVal＝result[nPos-1]；//獲取結果集最后

一個元素

if(tempVal＝＝endNode.key){//如果當前節點為

結束節點，將結果集中的節點放入路徑結果集中

for(let j＝0；j＜nPos；j++){

resultPath[pathNum][j]＝result[j]；

}

nPos- -；//回溯至目標節點的上一個節點

result[nPos]＝0；

pathNum++；//新增路徑數目

Mark[endNode.key]＝false；

break；

}；

while(startNode.flag＜matrix.length){

if(matrix[tempVal][startNode.flag]＝＝1){

if(Mark[startNode.flag]＝＝false){

var tempNode＝new Node()；

tempNode.key＝startNode.flag；

tempNode.flag＝0；

FindPath(matrix，tempNode，endNode)；

}

}

startNode.flag++；

}

if(startNode.flag＝＝matrix.length){

nPos- -；

startNode.flag＝0；

Mark[startNode.key]＝false；

break；

}

}

為了更好地理解算法，用例4進行簡要說明．

例 4有 5個節點的不確定隨機網絡，如圖 2所示．其中τAB、τBD、τDE是不確定權重，且分別具有正則的不確定分布?AB、?BD、?DE；ηAE、ηBC、ηCD是隨機權重，分別具有概率分布ΨAE、ΨBC、ΨCD，網絡中各邊的權重的分布函數見表 2．求距離節點 A最近的3個節點．

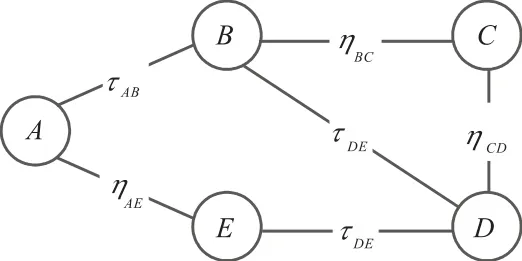
圖2 5節點不確定隨機網絡Fig. 2 Uncertain random network with 5 nodes

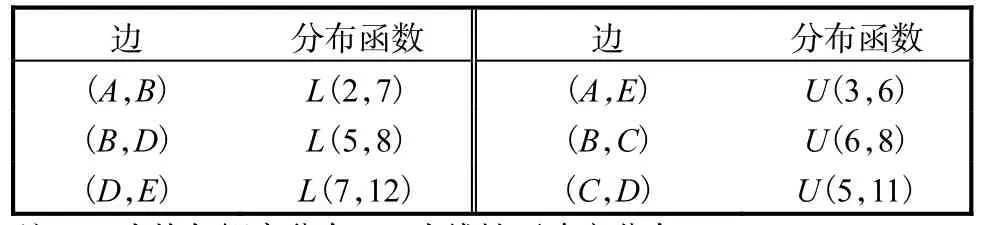
表2 圖2網絡中各邊的權重的分布函數Tab. 2 Distribution function of the edge’s weight of figure 2

能夠得到任意兩點間的路徑長度機會分布函數

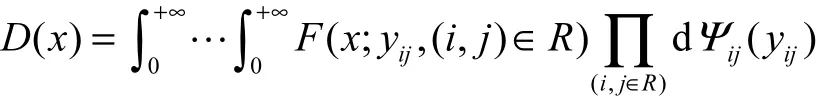
其中F( x,yij,(i,j)∈R)由它的逆不確定分布確定：

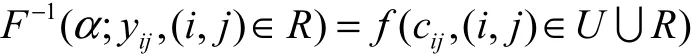
當機會測度α＝0.9時，計算出任意兩點間的最小路徑長度，計算結果見表3．

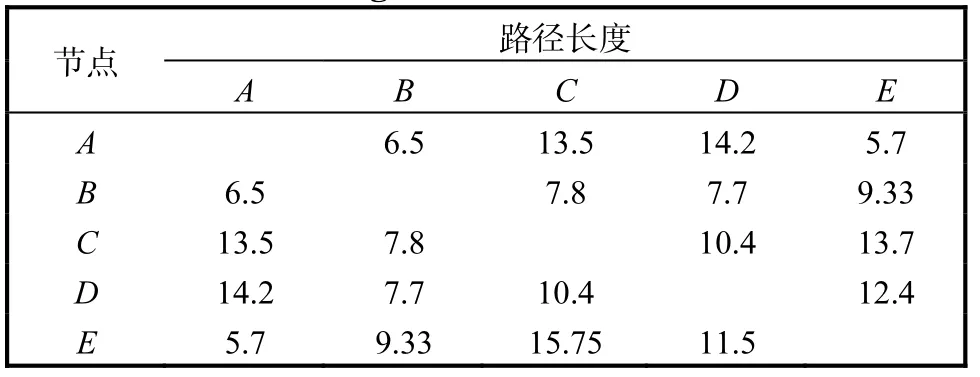
表3 α＝0.9時節點間路徑長度Tab. 3 Path length between nodes when α＝0.9

當機會測度α＝0.8時，計算出任意兩點間的最小路徑長度，計算結果見表4．

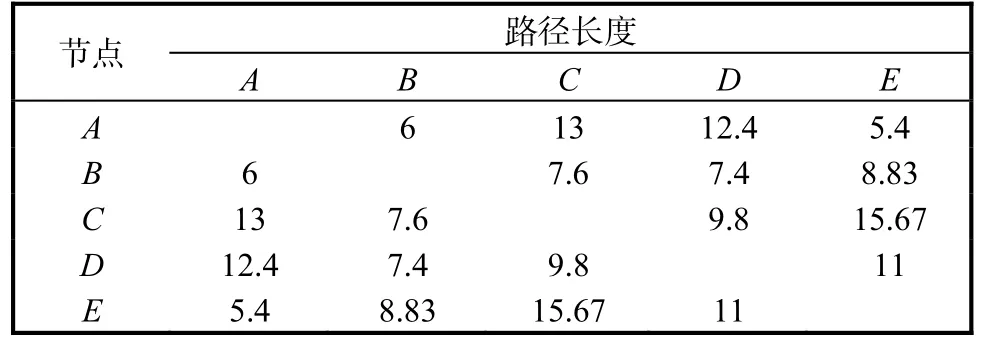
表4 α＝0.8時節點間路徑長度Tab. 4 Path length between nodes when α＝0.8

所以，當機會測度α＝0.9，k＝3時，距離節點A最近的 3個點分別為 E、B、C．當機會測度α＝0.8，k＝3時，距離節點A最近的3個點分別為E、B、D．

當機會測度變化時，查詢到的最短路徑節點也可能發生變化，所以需要根據現實需求來指定機會測度，以得到預期結果．

3 結 語

本文提出了不確定隨機網絡的 Top-k最近節點查詢問題，并使用機會理論求解該問題，設計不確定隨機網絡在一定機會測度條件下的 Top-k查詢算法．此算法能正確求解不確定隨機網絡的Top-k查詢問題，在網絡節點數目較小、不確定隨機分布較簡單時的效率較高；一旦網絡節點數目眾多、網絡非常復雜時，則計算的時間復雜度會較高．如何對算法進行改進，以提高算法的計算效率是下一步的研究方向．