分數階Liu混沌系統的Adomian分解法求解及數字實現

雷騰飛，陳 恒，付海燕

(1. 齊魯理工學院電氣信息工程學院，濟南 250200；2. 西京學院理學院，西安 710123)

17世紀 90年代，在整數階微積分提出不久，即出現了分數階微積分的概念．近年來，混沌動力學相關理論廣泛應用于各個領域[1]，其中隨著分數階系統的理論發展，以經典的混沌系統為研究對象，重新引入分數階微積分算子，即提出了許多分數混沌系統如分數階 Chen系統[2-3]、分數階 Lü系統[4]、分數階Lorenz系統[5]等．

目前，研究人員已在分數階混沌系統分析與控制領域取得一定的成果，但分數階混沌系統動力學分析的相關工作等卻是最近才開始，且相關文獻較少．關于分數階的定義較多，基于此的分數階微積分數值方法也存在不同[6]．文獻[7-9]將分數階模型通過拉氏變換到頻域中，利用高階系統模擬分數階系統，分別對分數階 Lorenz、分數階超 Qi、分數階超 Lorenz混沌系統進行基本動力學分析，同時采用模擬電路實現了相應的混沌系統．文獻[10]采用預估矯正法對分數階混沌進行同步控制研究．文獻[11-12]采用 Adomian分解法對分數階Chen以及Lü系統進行混沌特性的分析與研究，該方法的不足在于不可闡述分數階的記憶特性．

分數階 Liu混沌系統，一般稱為臨界混沌系統，該系統與經典的混沌系統(Lonrez系統、Chen系統以及Lü系統)存在不等價的拓撲，故對分數階Liu混沌系統的動力特性的探究討論尤為重要．若進一步利用改進的 Adomain分解法，則能夠更加準確地分析分數階Liu混沌系統的基本動力學，這對于認識分數階混沌系統的機理具有重要意義，特別是階數對系統的影響．

本文采用改進的 Adomian分解法對分數階 Liu混沌系統進行分解與數值仿真，根據數值仿真結果分析 0.9階的 Liu混沌系統的基本動力學行為．同時，利用DSP芯片實現了基于改進Adomian分解法的分數階Liu系統，從而說明分數階Liu混沌系統的混沌吸引子存在性，也為進一步在混沌密碼、機電耦合系統控制以及圖像、文字視頻加密領域的應用[13-14]提供參考．

1 分數階Liu混沌系統

文獻[15]提出經典的含有平方項的臨界Liu混沌系統，根據此系統可寫出分數階Liu混沌系統的動力學方程為

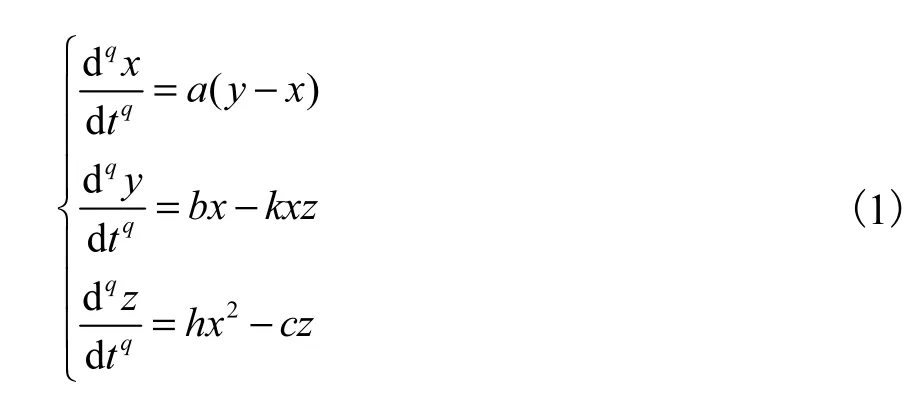
對式(1)系統進行非線性項的分解，截取前6項

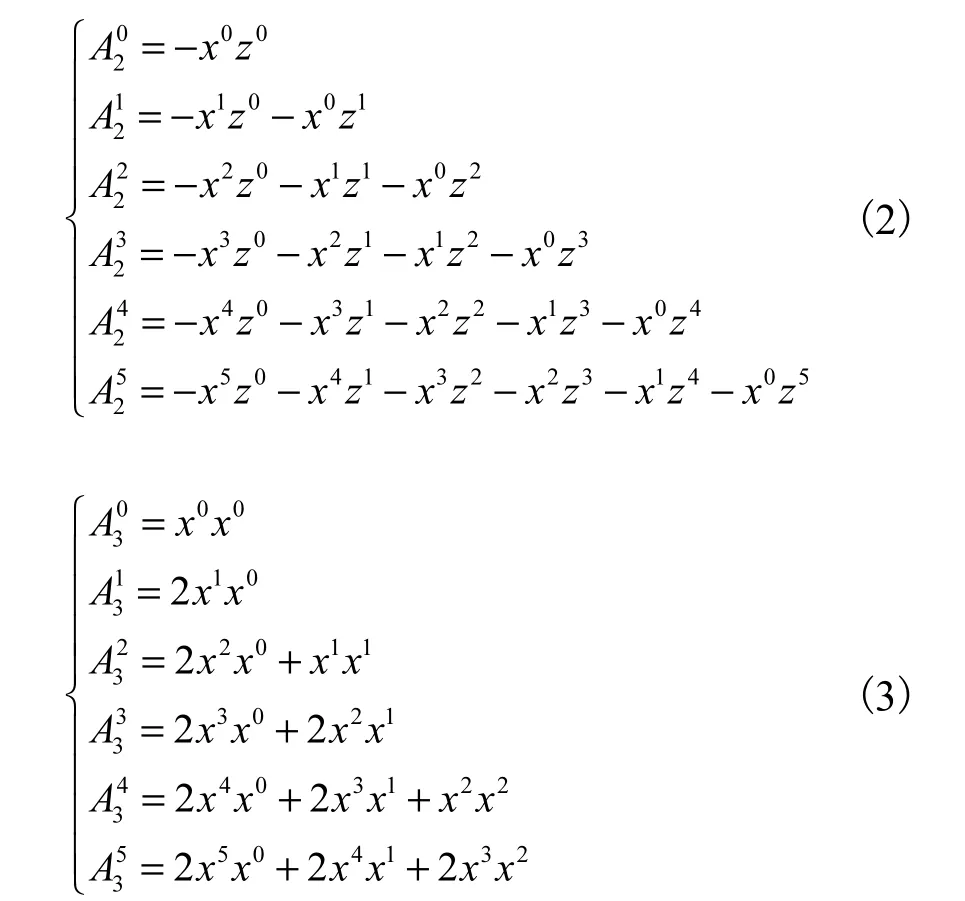
給定初始狀態：x0=x(t0)=c10，y0=y(t0)=c20，z0=z(t0)=c03，根據改進Adomian分解法[16]和分數階微積分性質得

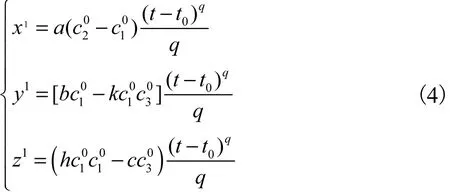
將相對應的變量賦系數值，令

可見，只需求出每一項對應的系數即可．根據改進Adomian分解法運算可知

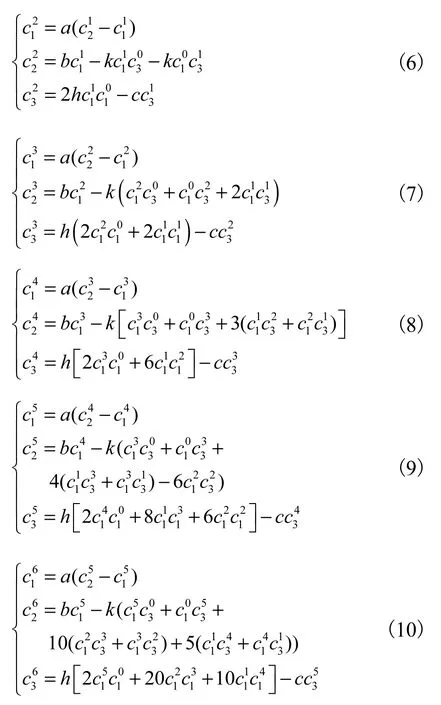
從而，得出系統的解

式中：x、y、z為系統變量；a、b、c、k、h、q 為系統參數，a＝10，b＝40，c＝2.5，k＝1，h＝4，q＝0.9．對上述 Adomain分解下的分數階 Liu系統進行數值仿真，即可得出式(1)系統的混沌軌跡，如圖1所示．

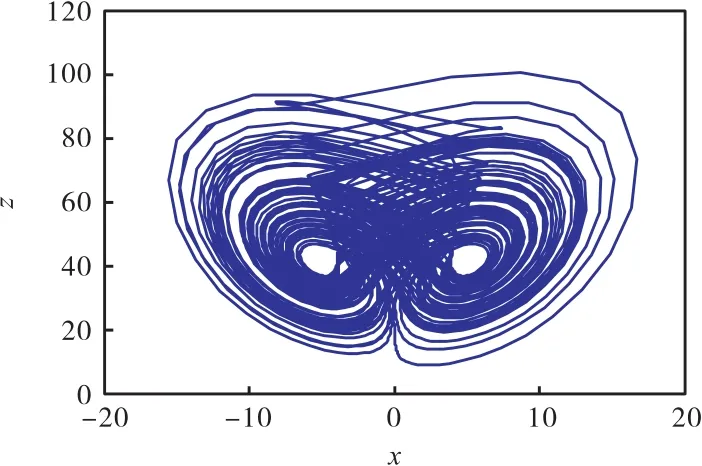
圖1 式(1)系統的軌跡圖Fig. 1 Phase portrait of system(1)

2 系統的分岔圖與復雜度

2.1 參數q的變化

分析了系統階數 q以及內部參數 a、b、c對分數階臨界混沌系統的分岔圖和復雜度[16]的影響．首先，固定內部參數，改變 q ∈[0.65,1]，從圖 2(a)的系統分岔圖可看出，系統在此區間處于混沌態；從圖 2(b)的復雜度SE和C0可以看出，隨著階數q增大，系統的復雜度在逐漸減小．

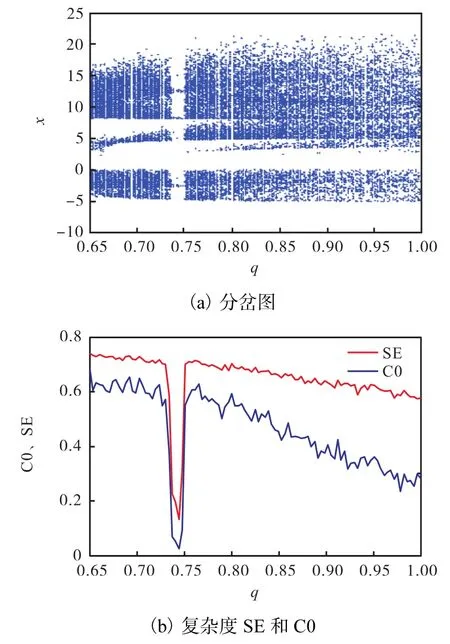
圖2 參數q變化時式(1)系統的分岔圖和復雜度Fig. 2 Bifurcation diagram and complexity of system(1)with parameter q

2.2 參數a的變化

令q=0.9，a ∈[5 ,20]，改變參數 a時系統的分岔圖、復雜度SE和C0如圖3所示．由圖3可知：分數階Liu系統以倍周期分岔進入混沌，即隨著參數a逐步減小，系統是通過倍周期方式進入混沌態；a ∈[5,14.7)屬于混沌狀態，此時系統的復雜度 SE相對值較大(0.6左右)，復雜度 C0相對值也較大(0.4左右)，總體此區間系統的復雜度較高；a ∈[1 4.7,20]屬于周期狀態，此區間內分叉圖數據點比較稀疏且成線狀出現，此時系統的復雜度SE處于0.1左右，復雜度C0處于0.05左右，系統復雜度相對較低．

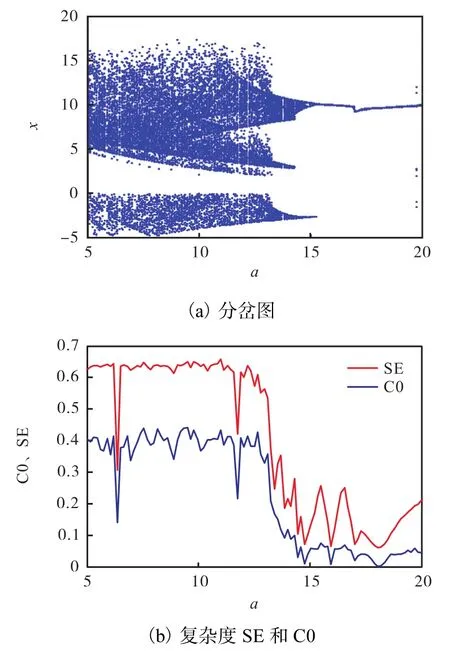
圖3 參數a變化時式(1)系統的分岔圖和復雜度Fig. 3 Bifurcation diagram and complexity of system(1)with parameter a

為了驗證上述分岔圖與復雜度的正確性，采用相圖法對具體參數下的相圖進行數值仿真，結果見圖4，圖 4(a)為混沌態，圖 4(b)為多周期態，圖 4(c)為雙周期態，圖4(d)為單周期態．

2.3 參數b的變化

令q=0.9，b ∈[0 ,60]，改變參數 b時式(1)系統的分岔圖和復雜度如圖5所示．由圖5可知：系統是以擬周期的行為進入混沌態；b ∈[0 ,6]時系統屬于非混沌狀態，此時分數階 Liu系統的復雜度 SE為0.38～0.6，復雜度 C0接近 0；b ∈(6,60]時系統處于混沌狀態，此區間對應的復雜度SE都處于0.6左右，從分岔圖可以看出 b ∈(10,20)有隔離帶，即陣發混沌態，相應點的復雜度值也較小．從分岔圖與復雜度SE可以看出，周期態部分存在差異，但復雜度C0一致，從而說明三者是相互補充的．對于參數 b具體值時的系統相圖，由于篇幅有限，不再給出．

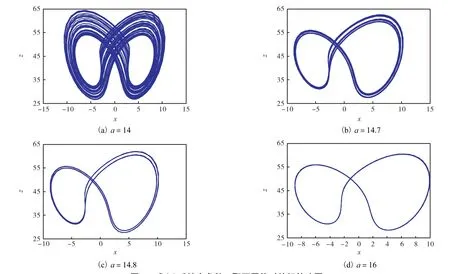
圖4 式(1)系統在參數a取不同值時的相軌跡圖Fig. 4 Phase portrait of system(1)with different parameter a

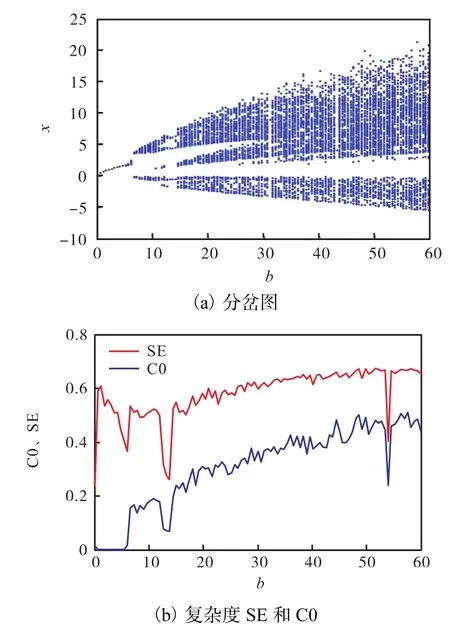
圖5 參數b變化時式(1)系統的分岔圖與復雜度Fig. 5 Bifurcation diagram and complexity of system(1)with different parameter b

2.4 參數c的變化

令q=0.9，c ∈[1,10]，改變參數 c時式(1)系統的分岔圖和復雜度見圖6．由圖6可知：此時系統是以倍周期分岔方式脫離混沌，與參數a變化時的方式相似．c ∈[8,10]時，系統屬于周期狀態，可以明顯觀察出分岔點的參數值范圍，此時系統的復雜度SE和C0均較低；c∈(1,8]時，系統屬于混沌狀態，復雜度 SE較高(取值范圍為0～1)，c＝6左右時分岔圖存在明顯的隔離，相應的復雜度值也較小．系統的相圖在參數 c變化時的仿真結果與參數a相似，本文沒有給出．

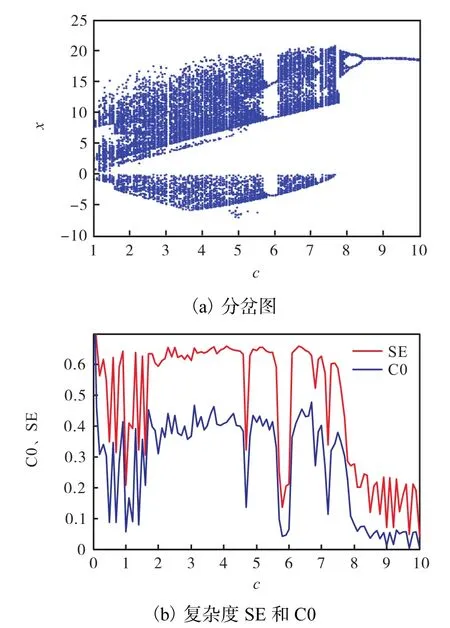
圖6 參數c變化時式(1)系統的分岔圖和復雜度Fig. 6 Bifurcation diagram and complexity of system(1) with different parameter c

3 系統的分岔空間

式(1)系統在雙參數變化下的復雜度 SE見圖7．從圖 7可以看出：系統分岔空間與單參數變化對系統的影響具有一致性，即圖7與圖3、圖5、圖6具有一致性．參數a與c同時變化，系統出現的混沌態較大，當然復雜度也較高，如圖7(b)所示．

圖7 雙參數變化時式(1)系統的復雜度SEFig. 7 Bifurcation space of system(1)

4 系統的數字實現

通常采用模擬電路搭建和實現混沌系統．與模擬電路相比，數字電路抗干擾能力強，隨著數字電路技術的發展，利用數字電路實現混沌系統特別是分數階混沌電路更有實際意義．數字信號處理芯片(DSP)采用 TI公司的 TMS320F28335，數模轉換芯片采用DAC8552，TMS320F28335與 PC間采用串口通信．TMS320F28335為浮點 DSP控制器，主頻為150MHz，精度高，運算快，可滿足復雜算法的運算需要．離散數據通過基本Adomian分解法產生，然后將離散值通過DMA(direct memory access)傳輸給數模轉換芯片．具體DSP硬件框架圖見圖8，系統硬件電路采用 TMS320F28335最小系統板(研旭最小系統板)搭建．

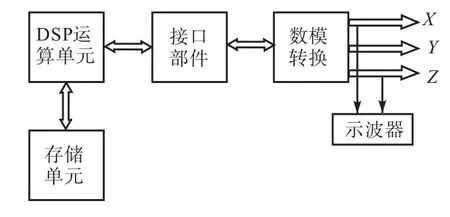
圖8 DSP硬件框架圖Fig. 8 DSP hardware framework diagram

將 DSP產生的混沌序列值先取小數點后 4位，且對于初值后的一段序列采用丟棄法，即取 3000～15000區間的序列，用示波器觀察到的系統吸引子見圖 9．

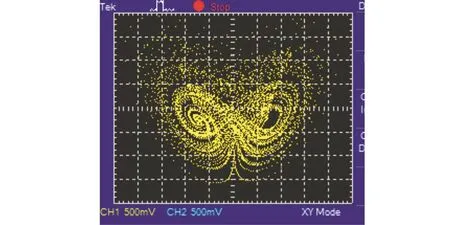
圖9 示波器觀察的系統吸引子Fig. 9 System attractor observed by oscilloscope

5 結 語

本文運用 Adomian分解法，從數值仿真方面分析一類經典的分數階Liu系統豐富的動力學行為，且根據參數 q的特點得出，隨著分數階的增大，系統復雜度減小．采用數字芯片 DSP實現分數階 Liu混沌系統，進一步說明系統的存在性與可實現性，同時也從一定意義上為分數階 Liu混沌系統的應用奠定了基礎．