影響塔里木盆地北緣綠洲非冰期水面蒸發的氣象因素分析*
(新疆喀什地區水利水電勘測設計院,新疆 喀什 844000)
蒸發是計算水量平衡的重要內容,其中:水面蒸發是水庫、湖泊等水體水量損失的主要組成部分。正確認識水面蒸發與各氣象因素之間的關系,對于干旱區水資源高效利用、農田灌溉管理具有重要意義[1]。
塔里木盆地是我國的極端干旱區,降水稀少,蒸發強烈。當地人類活動主要集中在沙漠邊緣的綠洲內,平原水庫作為綠洲灌區內重要的調節水源,為綠洲工農業生產提供了有效保障。但由于平原水庫水深淺、水面面積大、非冰期蒸發損失大,因此如何通過科學合理的調度管理減少平原水庫水面無效蒸發,節約寶貴的水資源,將是解決極端干旱區水資源嚴重短缺的一項重要途徑。
趙成義[2]等人以阿克蘇綠洲為例,分析了近30年不同口徑蒸發器水面蒸發量的變化趨勢,表明研究區蒸發量呈下降趨勢,水面蒸發量與水汽壓差、氣溫、風速有較好的相關關系,其中影響水面蒸發的主要因子是水汽壓差;魏光輝[3]等人以塔里木河下游鐵干里克氣象站2005年資料為例,采用熵值法對水面蒸發影響因素進行敏感性分析,結果表明溫度與風速對水面蒸發影響最為敏感;李萬義[4]以水汽壓力、風速和相對濕度為主要影響因素,建立了3因子水面蒸發預測模型;滕凱[5]以旬均最高氣溫、旬均風速、旬均飽和水汽壓和旬均日照時間為影響因素,建立了區域水面蒸發預測模型。
由于水面蒸發影響機理復雜,受觀測方法精細程度、氣候環境變化、觀測場地下墊面植被高度與海拔等因素影響,各區域的計算分析結論存在著不同。為探索塔里木盆地北緣綠洲區水面蒸發的主要影響因素,進而為建立該區域水面蒸發預測模型提供技術支持。本文以研究區內的尉犁縣非結冰期(2017年5—9月)日水面蒸發量觀測數據為例,采用主成分回歸方法,對研究區水面蒸發的主要因素進行分析,并取得了一些有價值的研究結果。
1 資料與方法
1.1 數據資料
選取新疆尉犁縣氣象站2017年5—9月逐日平均氣溫、最高氣溫、最低氣溫、日均風速、日均水汽壓、日均相對濕度、日照時數以及日蒸發量(E601蒸發器)8個氣象要素資料。
1.2 多重共線性診斷方法
采用方差膨脹因子(VIF)法[6],診斷自變量(各氣象因素)系統中是否存在多重相關性,表達式為:
(1)
式中Ri——自變量對其余自變量Xi進行回歸分析的復相關系數;
VIFi>10——各氣象因素間多重相關性嚴重。
1.3 主成分回歸方法
主成分分析法(Principal Component Analysis,簡稱PCA)是利用降維原理,把多指標轉化為少數獨立綜合指標的一種統計方法。
在主成分分析基礎上,選取前若干個有效荷載分量,就可建立多元回歸模型,進而分析各氣象要素指標與水面蒸發之間的定量關系。
2 模型計算
選取日均氣溫(x1,℃)、日最高氣溫(x2,℃)、日最低氣溫(x3,℃)、日均風速(x4,m/s)、日均水汽壓(x5,hPa)、日均相對濕度(x6,%)與日照時數(x7,h)這8個因素為自變量;日水面蒸發量(y,mm)為因變量。為保證模型可靠性,本文剔除了有日降水的數據,故模型樣本數為140組。
2.1 多重共線性診斷
利用SPSS 13.0軟件進行數據共線性診斷,計算結果見表1。由表1可知,各自變量(氣象要素)間存在嚴重多重共線性。

表1 方差膨脹因子
2.2 主成分分析
由于各氣象因素量綱不同,所以首先要將原始數據進行標準化處理,之后計算其數據相關性,相關系數矩陣見表2。
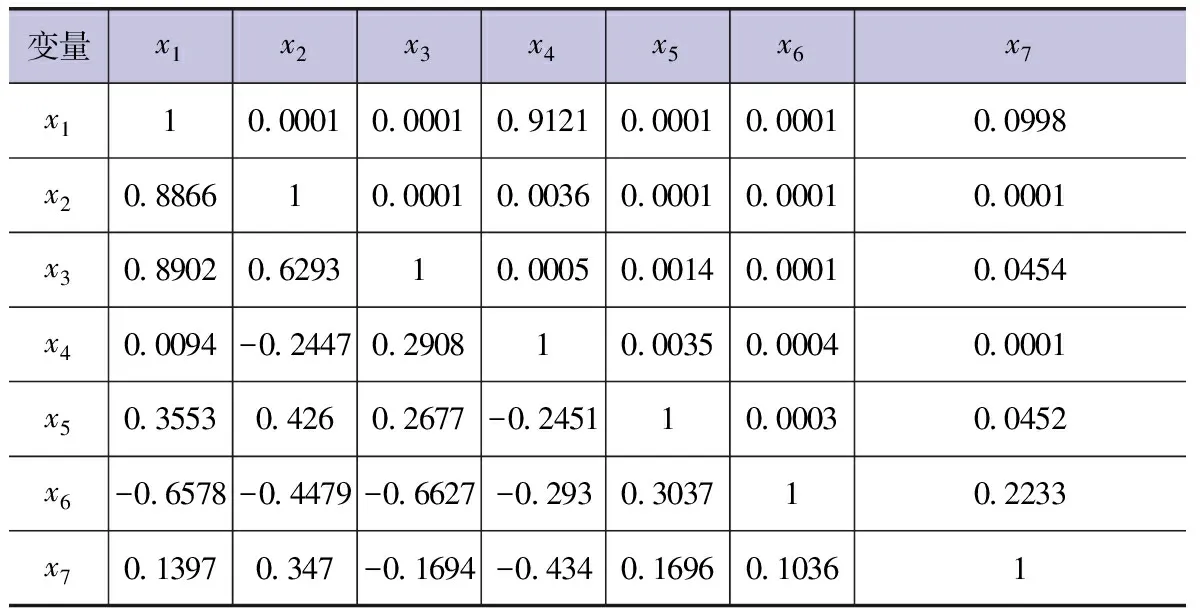
表2 相關系數矩陣
注左下角為相關系數,右上角為顯著水平,r0.01=0.217。
主成分特征值及貢獻率見表3,根據表3確定主成分個數為3(此時,方差累計貢獻率為88.0%)。
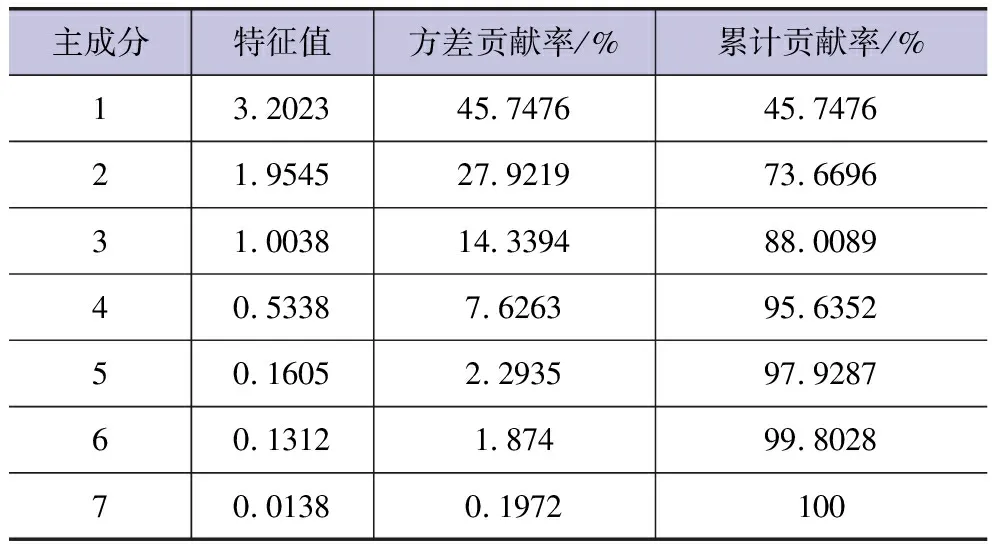
表3 主成分特征值及貢獻率
根據確定的主成分個數,采用方差極大正交法求得主成分荷載值(見表4)。
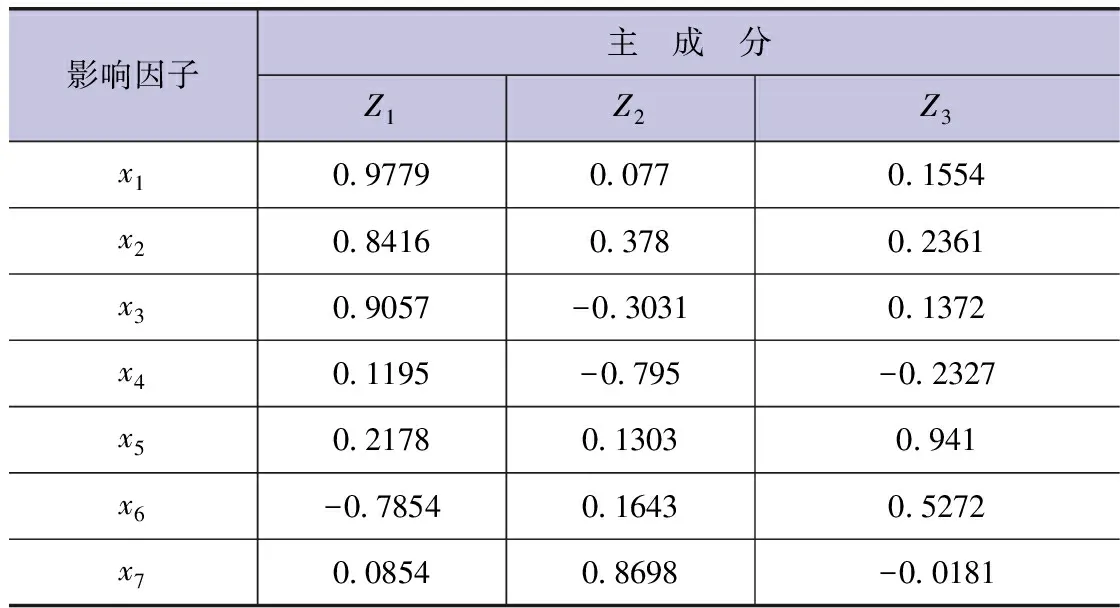
表4 主成分荷載值(不考慮日降水情況)
根據表4可知:第1主成分(Z1)可作為溫度與濕度的描述指標,包含了日均氣溫、日最高氣溫、日最低氣溫與相對濕度這4個因素,解釋了全部數據信息的45.75%;第2主成分(Z2)包含了風速與日照2個因素,解釋了全部數據信息的27.92%;第3主成分(Z3)主要包含水汽壓因素,解釋了全部數據信息的14.34%。3個主成分包含原有7個指標的88.0%的數據信息。
2.3 主成分回歸分析
將上述3個主成分代替原自變量進行回歸分析,得到標準化自變量與應變量間的回歸模型:
y=10.968+1.151z1-0.735z2-0.447z3
(n=140,r=0.8748,r0.01=0.217)
(2)
式中n——樣本數;
r——方程擬合相關系數;
r0.01——顯著性為0.01時的方程臨界相關系數。
所建主成分回歸方程,各回歸系數均通過t檢驗,達到極顯著水平(見表5)。
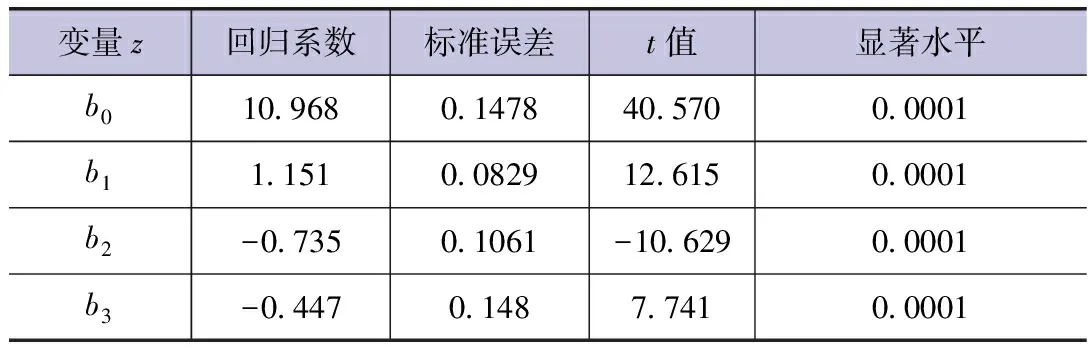
表5 主成分回歸方程系數值(不考慮日降水情況)
2.4 日降水情況下的主成分回歸模型的建立
為了檢驗有降水的日數據對主成分回歸模型相關參數的影響,將有降水的日氣象數據代入上述模型(共計153組觀測資料),經計算得到模型主成分荷載值(方差極大正交法)與回歸方程系數值,見表6、7。
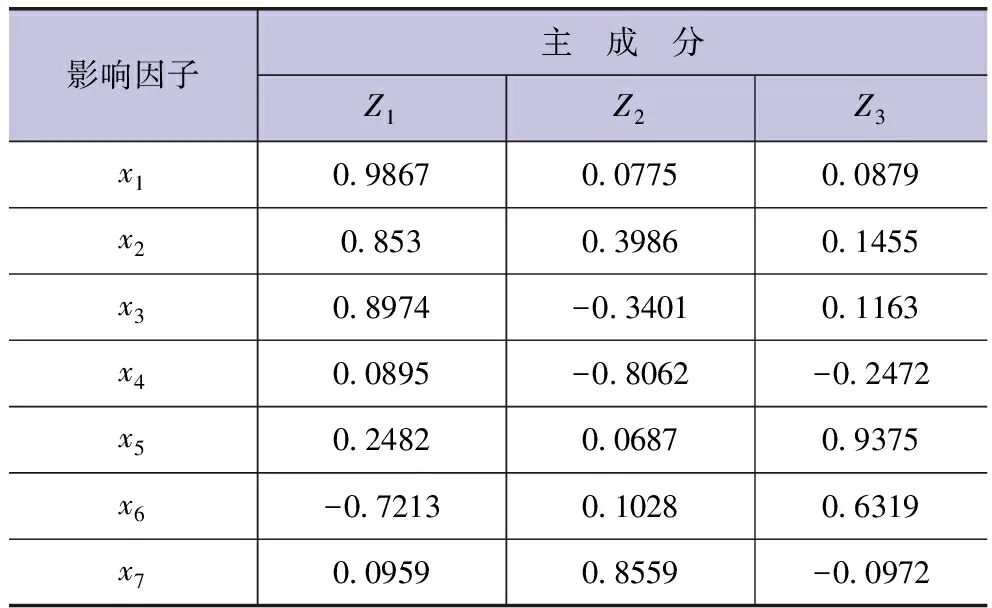
表6 主成分荷載值(考慮日降水情況)
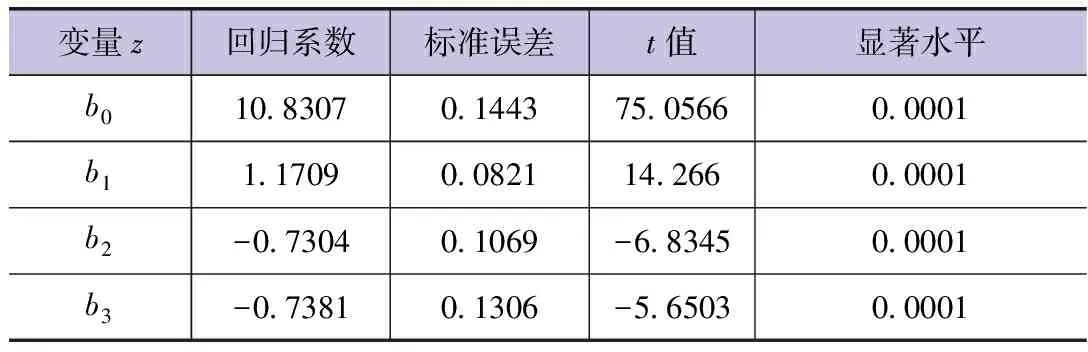
表7 主成分回歸方程系數值(考慮日降水情況)
3 結果分析
3.1 不考慮日降水情況下的對比分析
選用不考慮降水影響的140組樣本,用7個基本氣象要素建立的水面蒸發多元線性回歸方程如下:
Y= -7.894+0.936x1-0.059x2-0.301x3+2.119x4-0.213x5-0.001x6+0.175x7(n=140,r=0.9108,r0.01=0.217)
(3)
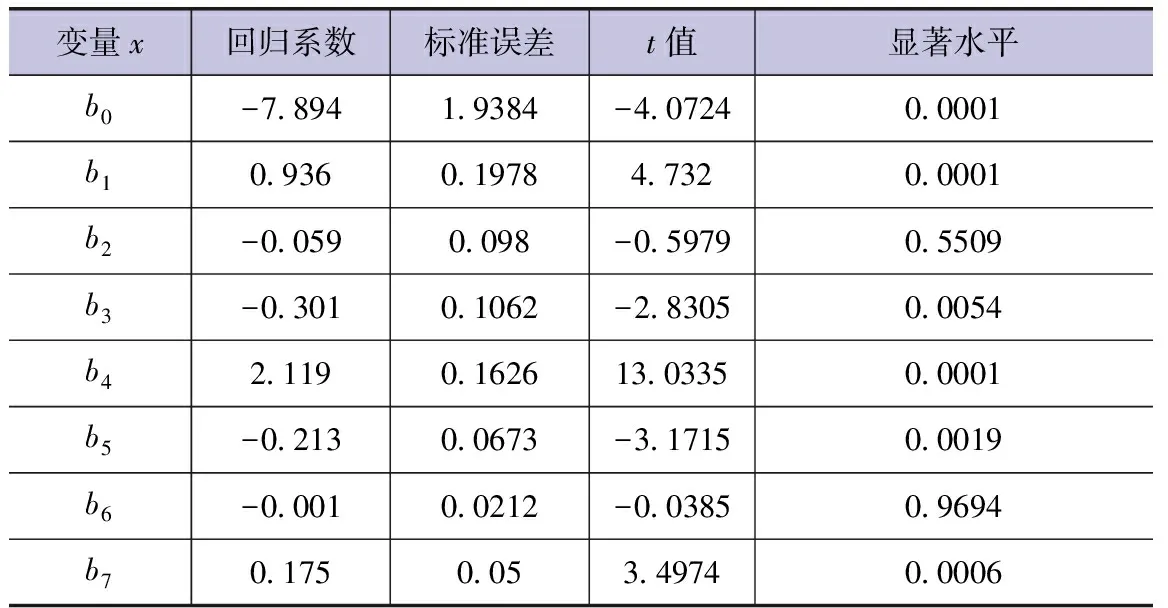
表8 多元線性回歸方程系數值(不考慮日降水情況)
由表8可知,式(3)擬合效果優于式(2),但方程回歸系數b2、b6均未通過t0.01檢驗。而且從方程的物理成因來講,式(3)中水面蒸發將會隨著日最高氣溫與日最低氣溫的升高而減小(假設其他氣象因素不變的情況下),與實際情況不符。
3.2 考慮日降水情況下的對比分析
考慮降水影響的153組樣本數據,用7個基本氣象要素變量建立的水面蒸發多元線性回歸方程如下:
Y= -7.207+0.925x1-0.054x2-0.315x3+2.132x4-0.237x5-0.015x6+0.222x7(n=153,r=0.9147,r0.01=0.208)
(4)
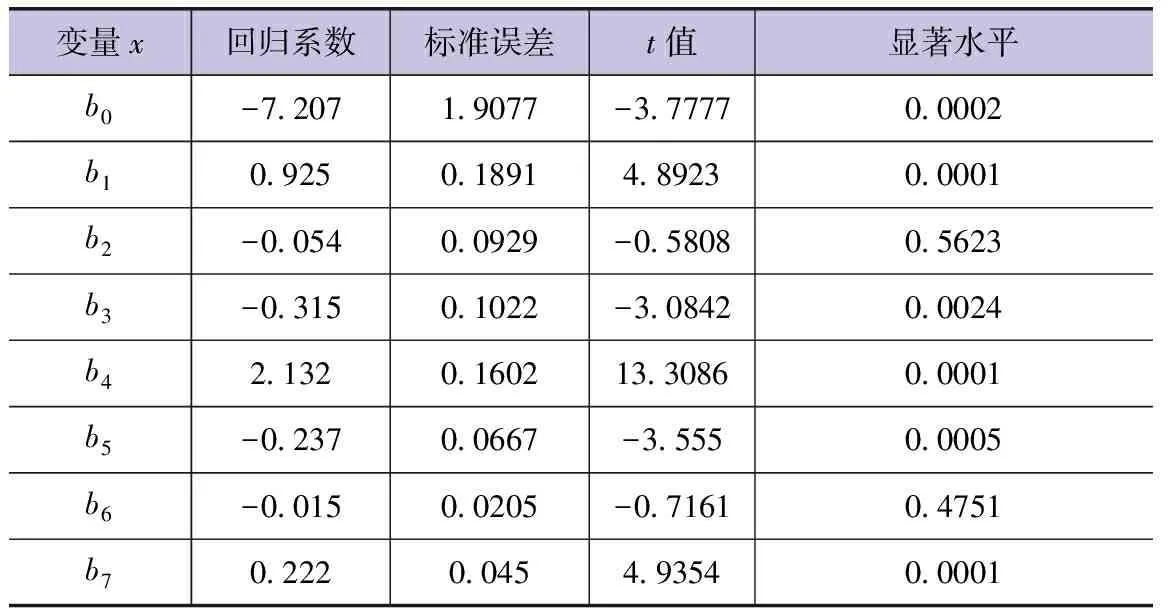
表9 多元線性回歸方程系數值(考慮日降水情況下)
由表9可知,方程回歸系數b2、b6均未通過顯著性檢驗。且將式(4)與式(3)進行對比可以發現,在考慮日降水的情況下,所建立的模型回歸系數數值與原模型有一定出入,但回歸系數的正負情況未發生變化。
4 討 論
a.水面蒸發量影響因素的計算尺度不一樣(如采用日、旬、月、年計算尺度),也會導致主成分分析結果隨著計算尺度的變化產生一定的變化。水面蒸發影響因素計算結果在一定程度上還會受數據計算尺度的影響。
b.將日降水數據帶入主成分回歸模型,會對原模型回歸參數的數值大小產生一定影響,但不會影響回歸參數數值的正負。同時,由于日降水數據樣本數只有13組,剔除日降水數據后的樣本數為140組,日降水數據樣本占總樣本的比例不到10%,故考慮日降水情況時,并不會影響模型在水面蒸發主要影響因素判定上的正確性。
c.氣溫能直接影響水汽擴散的速度和接納水汽的能力,氣溫較高時,水面上的飽和水汽壓大,水汽壓差大,易于水面蒸發;水面氣溫高時,水分子運動能量大,水面蒸發強度越大。風速越大,水面上部的水汽壓差越大,水汽交換越頻繁,水面蒸發就越強烈。相對濕度能反映出空氣中的水汽含量距離飽和時的程度和交換的速度。當相對濕度較小時,水汽向外擴散和交換強度增強,蒸發強度越大;相對濕度增大后,既對水面水分子的外逸有抑制作用,也使水汽的擴散和交換強度減弱,蒸發強度減小。因此,本文所得結論合理。
5 結 論
a.本文根據新疆尉犁縣2017年非冰期日氣象觀測數據建立了水面蒸發與主要影響氣象因素間的主成分回歸模型,該模型通過顯著性檢驗,可用來分析研究區日水面蒸發變化。
b.影響研究區域水面蒸發的主要氣象因素為氣溫、相對濕度、風速與日照時數,這為內陸干旱區水資源合理利用與科學管理提供了理論支持。

