基于鳥群算法的土壤水分特征曲線模型參數估算*

(山西省水利水電科學研究院，山西 太原 030002)

隨著科學技術不斷發展，計算機數值計算方法已經成為解決土壤中高維非線性問題的重要工具。水力參數差異是導致土壤水分時空變異的重要因素，而土壤水分特征曲線是關鍵的土壤水力參數之一。土壤水分特征曲線反映了土壤水分能量和數量之間的關系，是進行土壤水分運動模擬的基礎條件。因此，如何精準獲取土壤水分特征曲線模型參數對于準確實現水分時空動態預測具有十分重要的意義。

Van Genuchten模型具有較高的預測精度，并且模型參數的物理意義也最為明確，因此，該模型被廣泛用于土壤水分特征曲線的定量描述。目前，該模型參數的確定主要包括入滲試驗法和數學計算法[1-2]。相對于入滲試驗法，數學計算法更加簡單方便。但采用前人的數學計算方法進行參數估算時，也存在一定不足。李春友[3]采用單純形調優法進行了水力參數估算，結果表明該方法會陷入局部最優，因此，它不是一種合適的算法。馬英杰[4]采用非線性阻尼最小二乘法進行了水力參數的估算, 但模型預測結果受初始值影響較大，模型精度并不穩定。因此，尋找一種更加合適的算法對于提高Van Genuchten模型預測精度是非常必要的。鳥群算法是一種基于模仿鳥類種群活動過程(覓食、警戒和飛行)而提出的新型全局智能優化算法。該算法具有調節參數少、收斂精度高和魯棒性能好等優點，在電網優化調度、水庫優化調度和年徑流量預測等方面取得了較好的應用效果[4-6]，但在農業土壤環境方面未見相關報道。該算法對Van Genuchten模型的參數優化能力及效果也尚不清楚，有待進一步研究。為此，本文將采用該算法對Van Genuchten模型參數進行求解計算和精度評價，以期為Van Genuchten模型參數的估算提供一種新途徑。

1 Van Genuchten模型參數求解方法構建

1.1 Van Genuchten模型簡介

本文采用Van Genuchten模型對土壤水勢與含水率的關系進行描述，具體數學表達式如下[7]：

(1)

式中θ——土壤含水率，cm3/cm3；

h——土壤水吸力，cm；

θs——土壤飽和含水率，cm3/cm3；

θr——土壤殘余含水率，cm3/cm3；

α、m、n——土壤水分特征曲線形狀參數，m=1-1/n，n>1。

1.2 構造目標函數

由式(1)可知，θs，θr，α和n為4個獨立參數。為此，本文構造的目標函數見式(2):

(2)

式中θs——實測含水率，cm3/cm3；

hi——實測含水率θi對應的土壤水吸力，cm；

θ(hi,X)——含水率計算值，cm3/cm3；

X——待求參數向量(θs，θr，α,m)；

N——樣本數。

1.3 鳥群(GSA)算法基本思想

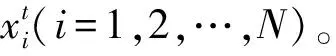
a.覓食行為。通常，鳥類在覓食過程中都需要隨時保持警惕性，即覓食行為和警戒行為需要進行切換，并且該過程為一個隨機發生過程。這可以用數學語言描述為：在(0,1)范圍內，當均勻分布的隨機小數小于P[P∈(0,1)]時，鳥群進行覓食，否則，保持警惕。在覓食過程中，每只鳥都能對食物及群體以往最好經驗進行及時記錄和更新，并且這種群體信息是共享的。這些可以采用數學模型進行描述，見式(3):

(3)

式中j——1,2,…,D;

C——非負常數，認知行為的加速因子；

S——非負常數，是群體行為的加速因子；

Pi，j——第i只鳥最佳位置；

gj——群體當前最佳位置。

b.警戒行為。在警戒行為發生時，個體均會向群體靠攏。由于個體存在警覺性差異，它們向群體中心移動的難易程度也會各不相同，并且在這種移動過程中還會伴隨著相互競爭。該警戒行為可采用下式進行描述：

(4)

(5)

(6)

式中k(k≠i)——(1,N)之間的正整數；

a1和a2——(0,2)之間的實數；

PFiti——第i只鳥最佳適應度；

sumFit——鳥群適應度之和；

ε——常數；

meanj——群體第j維平均位置。

c.飛行行為。在鳥群尋找食物過程中必然會發生飛行行為。由于個體差異，個體間的生存能力會存在差異。部分群體能夠及時準確發現食物，成為生產者；而另外群體只能跟隨生產者獲取食物，成為食物索取者。生產者和隨機者的出現為隨機過程。飛行行為可采用下式進行描述：

(7)

(8)

式中randn(0,1)——服從方差為0，均值為1的Gaussian分布的隨機數；

k——(1,N)之間的正整數；

FL[FL∈(0,2)]——索取者會跟隨生產者去尋找食物。

另外假設每只鳥會在FQ時間間隔內飛往另一個地方，FQ為正整數。

1.4 Van Genuchten模型參數尋優流程

Van Genuchten模型參數尋優主要包括如下步驟：

步驟1：初始化鳥群規模N、迭代次數M、飛行頻率FQ、覓食概率P和常量參數。

步驟2：根據適應度函數計算個體適應度值，并由此確定個體和群體的最佳位置。

步驟3：迭代開始，判斷t%FQ是否有余數。

a.有余數，判斷鳥群發生覓食行為還是警戒行為。若為覓食行為，采用式(3)更新位置；若為警戒行為，采用式(4)更新位置。

b.若沒有余數，判斷個體屬于生產者還是索取者。若為生產者，采用式(7)更新位置；若為索取者，采用式(8)更新位置。

步驟4：若第i只鳥當前位置優于先前自身最佳位置，則將當前位置更新為自身最佳位置，同時更新鳥群當前最佳位置。

步驟5: 判斷是否達到最大迭代次數，若迭代結束轉至步驟6; 否則迭代數加1，轉回步驟3。

步驟6: 輸出鳥群最佳適應度值及鳥群最佳位置所包含的θs，θr，α和n為4個獨立參數。

1.5 模型評價

本文主要從模型預測值與實測值的線性一致性、平均相對誤差(MAPE)、均方根誤差(RMSE)三個方面對模型預測效果進行評價。MAPE和RMSE的計算式分別為：

(9)

(10)

式中WR——試驗觀測值,mg/kg;

WL——模型預測值,mg/kg;

N——樣本數。

2 數據來源

本文采用室內土壤水分特征曲線試驗資料對Van Genuchten模型參數進行估算。土壤取樣點位于山西省水利水電科學研究院節水高效示范基地。該基地位于太原市小店區，屬暖溫帶大陸性氣候區，年平均降水量為495.5mm，年平均氣溫為9.5℃。土壤經風干、碾壓、混合、過篩(篩孔徑為2mm)后備用。土壤質地為黏壤土。首先通過壓力膜儀法獲得土壤水分特征曲線數據資料，然后采用單純形調優法、非線性最小二乘法和鳥群算法分別對Van Genuchten模型參數進行優化求解。

3 參數估算分析

3.1 Van Genuchten模型參數估算結果分析

本文采用鳥群算法對Van Genuchten模型參數進行求解，獲得的最優模型參數見下表。為了進一步評價該方法的可靠性和優越性，采用傳統的單純形調優法和非線性最小二乘法獲得的估算結果作為對比，模型參數見下表。由下表可以看出，經單純形調優法和非線性最小二乘法計算后的土壤飽和含水率(θs)數值相同，獲得的土壤殘余含水率θr數值也相同。而經過鳥群算法處理后的θr要比前兩者結果大11.99%，θs要比前兩者結果小0.73%。由此說明，鳥群算法對θr的估算結果影響較大。從形狀參數來看，經單純形調優法和鳥群算法估算后的形狀參數α數值相同，而非線性最小二乘法估算結果要比其余2種方法的估算結果高3.08%，由此說明3種方法處理后的α數值差異不明顯。由下表還可以看出，經3種方法處理后的形狀參數n大小表現為：單純形調優法>非線性最小二乘法>鳥群算法。相對單純形法而言，經非線性最小二乘法和鳥群算法估算后的參數n要分別比前者小0.98%和2.00%，說明3種算法對形狀參數n的計算結果無顯著影響。由下表還可以看出，3種方法估算方法的均方差大小表現為：非線性最小二乘法>單純形調優法>鳥群算法。綜上所述，與傳統的單純形調優法和非線性最小二乘法相比較，基于鳥群算法的參數估算方法主要對Van Genuchten模型中參數θr的影響較大。基于鳥群算法的Van Genuchten模型參數估算方法的結果更加準確。

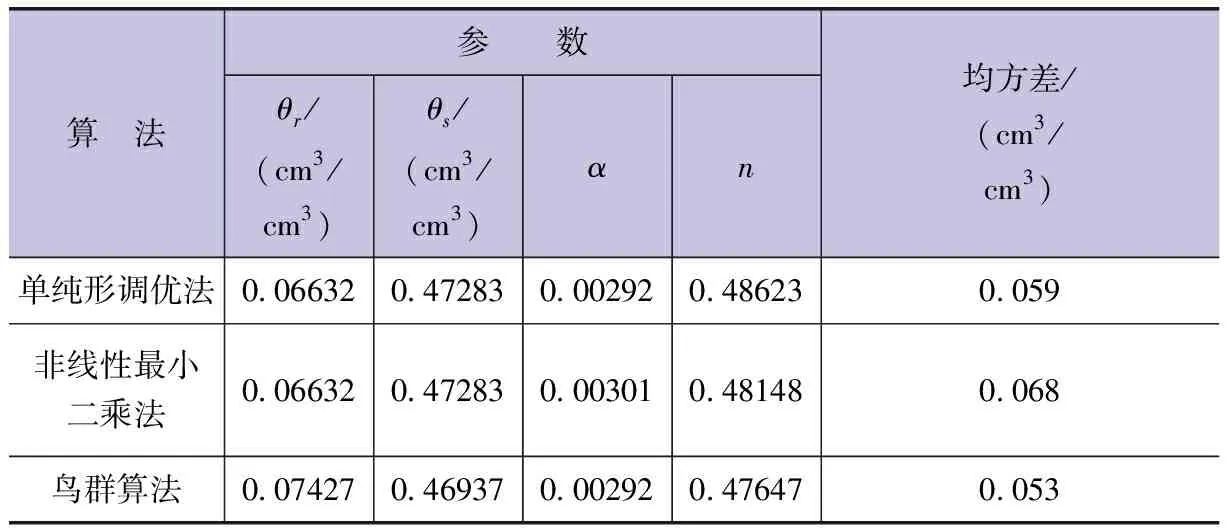
Van Genuchten模型參數估算結果表

3.2 Van Genuchten模型參數估算精度分析

圖1為不同估算方法下土壤含水率預測值與實測值間的線性關系。由圖1可以看出，經3種算法處理后的估算值與實測值均呈現較好的線性關系。經單純形調優法、非線性最小二乘法和鳥群算法處理后的線性方程斜率分別為0.904、0.968和0.974，決定系數分別為0.987、0.992和0.996。由此說明，經3種方法處理后，實測值與預測值間線性一致性好壞表現為：鳥群算法>非線性最小二乘法>單純形調優法。

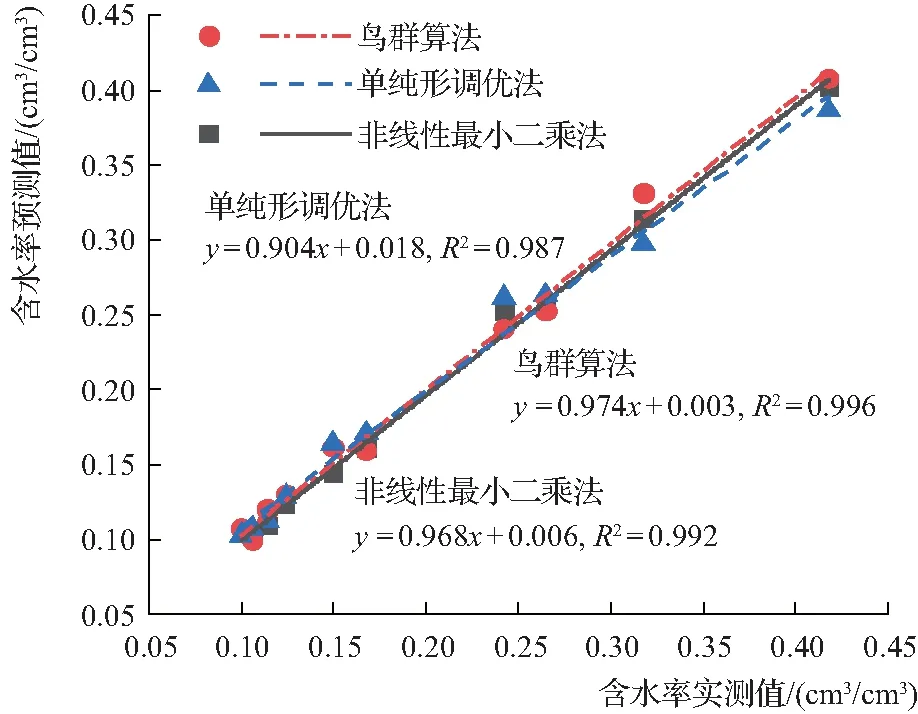
圖1 不同估算方法下土壤含水率預測值與實測值間的線性關系

圖2為不同估算方法下土壤含水率預測值與實測值對比結果。由圖2可以看出，經3種方法估算后的土壤含水率均隨土壤水吸力呈指數型衰減趨勢。由圖2可以看出，在0～2000cm和9000～12000cm范圍內，3種算法處理后的結果較為接近，但在2000～9000cm范圍內，3種算法處理后的結果差異較為明顯。由此說明，不同算法主要對中間土壤水吸力段(2000～9000cm)的土壤含水率預測結果影響較大。從整體上來看，經鳥群算法處理后的含水率預測值與實測值最為接近，單純形調優法的處理結果次之，非線性最小二乘法的含水率預測值與實測值差異最明顯。

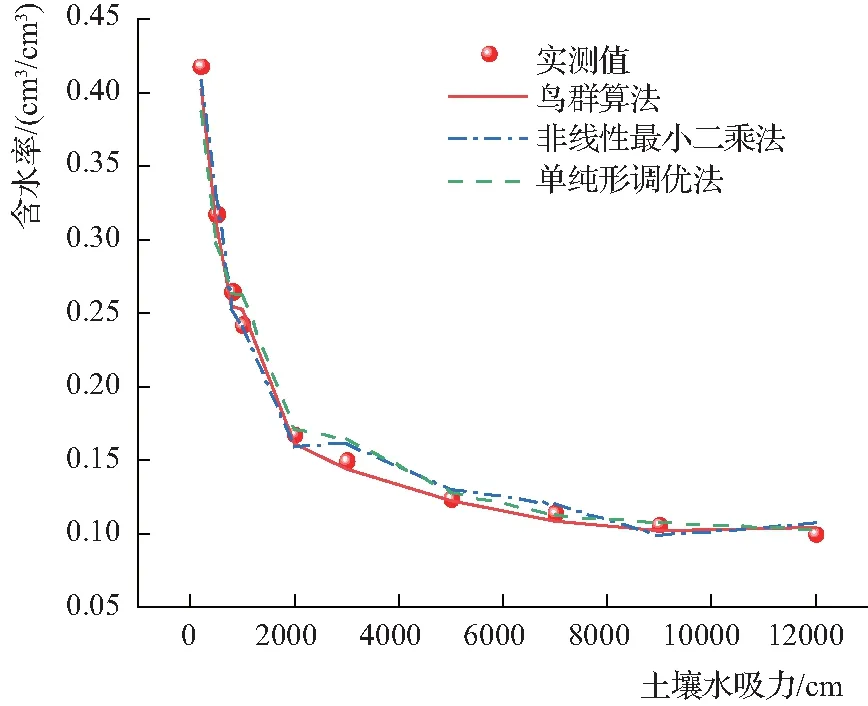
圖2 不同估算方法下土壤含水率預測值與實測值對比結果

為了進一步準確比較各種方法的估算效果，有必要對其進行量化分析。圖3為不同算法估算值與實測值間的絕對百分誤差。由圖3可以看出，不同算法處理后的樣本誤差較為明顯。經鳥群算法、非線性最小二乘法和單純形調優法處理后的絕對百分誤差分別為1.00%～4.84%、0.74%～7.78%和0.57%～9.69%，平均相對誤差分別為3.50%、4.89%和4.31%。由此說明，不同算法的估算精度好壞表現為：鳥群算法>單純形調優法>非線性最小二乘法。鳥群算法的估算效果最為理想，單純形調優法估算效果次之，非線性最小二乘法估算效果最差。

圖3 不同算法估算值與實測值間的絕對百分誤差

4 結 論

本文通過鳥群算法對Van Genuchten模型中的參數進行了求解，并對參數估算精度進行了評價。與單純形調優法(SEM)和非線性最小二乘法(NLS)的估算結果相比較，基于鳥群算法(BSA)的參數估算方法獲得的土壤殘余含水率θr均比前兩者要大11.99%。基于鳥群算法的Van Genuchten模型參數估算方法的平均相對誤差僅為3.50%，優于傳統的單純形調優法和非線性最小二乘法估算效果。