滑翔飛行器反逆軌攔截突防制導律研究

劉開封，孟海東，王長江，李軍營，陳穎

(火箭軍研究院 第六研究所，北京 100094)

0 引言

動能攔截器(kinetic kill vehicle, KKV)助推級一旦關機，其僅能利用軌控發動機提供機動加速度，由于軌控發動機可用加速度有限，決定了KKV攔截范圍也有限[1-2]。高超聲速滑翔飛行器具有速度快、機動能力強和軌跡難以預測的特點[3-5]，因此KKV助推級很難將其推進至理想攔截狀態，若KKV與助推級分離時刻狀態與理想攔截狀態存在偏差，則高超聲速滑翔飛行器可利用其速度快、機動能力強的特點逃逸KKV攔截范圍。

本文基于假設條件，從逃逸KKV機動攔截范圍的角度，首先分析了高超聲速滑翔飛行器利用空氣動力反逆軌攔截機動突防的可能性，然后根據動能攔截器助推分離時刻的狀態參數推導了機動突防制導律，最后對推導的機動突防制導律進行了仿真驗證。

1 反逆軌攔截機動突防可能性分析

1.1 前提條件

本文反逆軌攔截機動突防方法，是基于以下前提條件展開的：

(1) 由于從KKV與助推級分離到攔截交會時間很短(一般為幾秒至十幾秒)，因此可假設地球為不旋轉圓球；

(2) 由于攔截末段突防飛行器與KKV高度相差不大，且位置偏差相對于地球半徑也為小量，因此可近似認為攔截雙方重力加速度相同，則重力加速度對攔截雙方產生的速度和位置變化也相同，因此可不考慮重力加速度對雙方的影響，即認為為零重力加速度環境；

(3) 由于KKV氣動參考面積較小，因此可忽略KKV空氣動力；

(4) KKV可向任意方向提供加速度；

(5) KKV助推分離時刻紅外特性變化明顯，因此假設突防飛行器能夠獲取KKV分離時刻狀態參數。

1.2 機動突防可能性分析

在上述條件下，若KKV軌控發送機最大可用加速度為aI，KKV與助推級分離時刻t0的初速為vi0，則KKV最大機動范圍如圖1所示，為以vi0為對稱軸的“喇叭形”區域[6]，t時刻最大機動半徑Ri(t)為

Ri(t)=0.5aI(t-t0)2

.

(1)

因此，不難量化出最大機動半徑，如圖1所示。

若KKV與助推級分離時刻，攔截雙方速度方向均位于視線方向且方向相反，稱為理想攔截條件。如圖1所示，圖中m0和vm0分別為KKV與助推級分離時刻突防飛行器位置和速度矢量，i0和vi0分別為KKV與助推級分離時刻KKV位置和速度矢量。若突防飛行器可用加速度小于攔截器可用加速度，在不考慮KKV探測、控制誤差和延時的情況下，顯然突防飛行器無法突破KKV攔截。

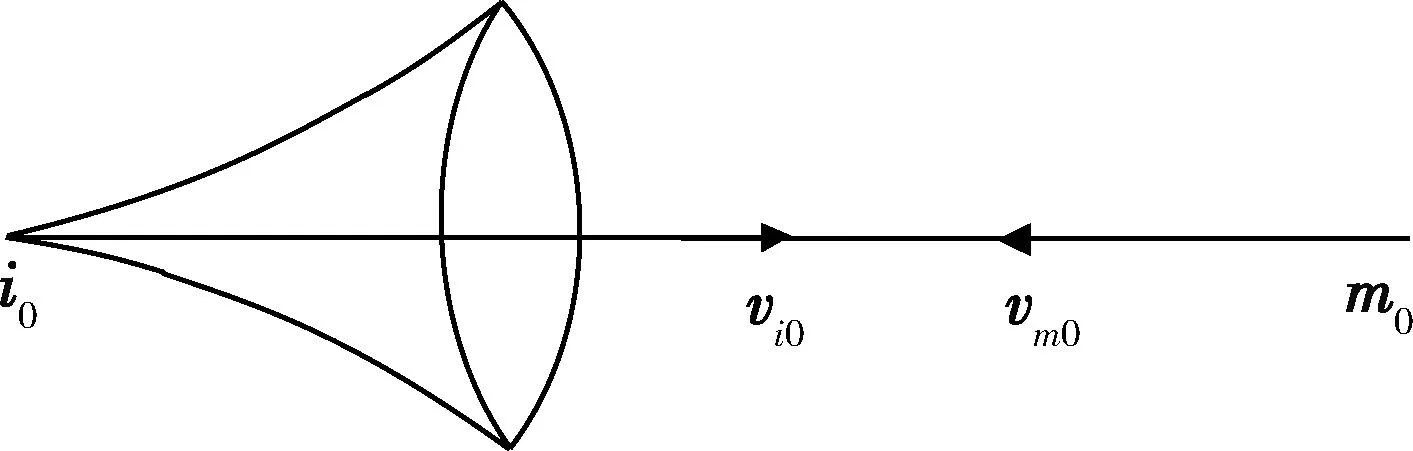
圖1 KKV理想攔截條件示意圖Fig.1 Perfect interception condition of KKV

但由表1可以看出，KKV機動范圍并不大，而突防飛行器的速度很大，如果vm0和vi0方向存在偏差，則可能逃出KKV攔截范圍。

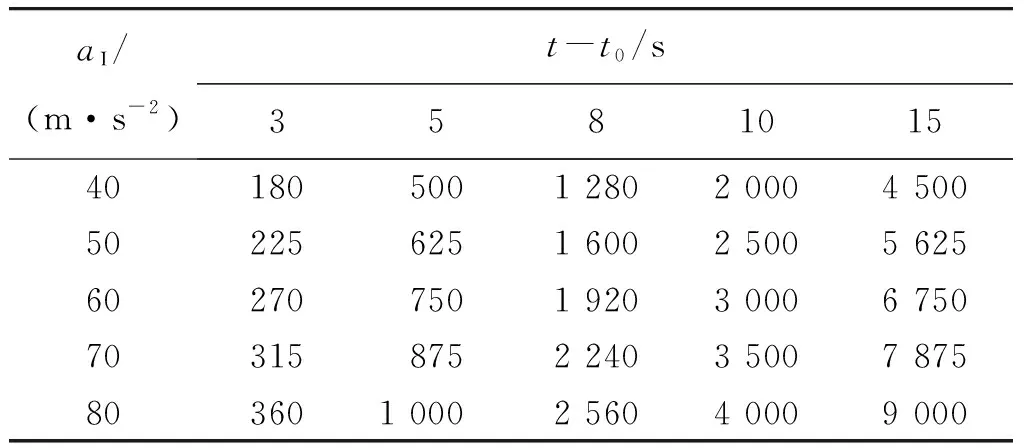
表1 KKV最大機動半徑Ri對照表

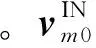
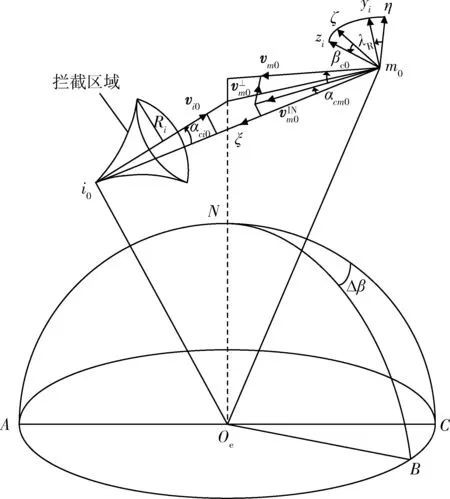
圖2 逆軌攔截示意圖Fig.2 Anti-head-on interception schematic

定義北天東坐標系(m0xnynzn)[7]，該坐標系的原點O1位于突防飛行器質心；O1yn軸在地心與突防飛行器質心連線方向上；O1xn軸在過突防飛行器質心的子午面內且垂直于O1yn軸，指向北極為正；O1zn與O1xn，O1yn構成右手直角坐標系。

定義視線坐標系(O1ξηζ)[7]，該坐標系的原點位于突防飛行器質心O1；O1ξ軸由突防飛行器指向攔截器；O1ζ軸位于北天東坐標系O1xnzn平面內，且與O1ξ軸垂直，順O1ξ看去O1ζ指向右側；O1η與O1ξ,O1ζ構成右手直角坐標系。

并定義攔截坐標系(m0xiyizi)，原點位于m0，該坐標系m0xi軸與視線重合，m0yi軸位于初始攔截平面法向，方向與vi0×m0i0方向相同，m0yi按右手定則確定，攔截坐標系為慣性坐標系，原點和坐標軸方向不隨突防雙方狀態改變而改變。由于m0xi軸與視線重合，t0時刻視線坐標系與攔截坐標系僅存在一個歐拉角λR，t0時刻攔截坐標系、視線坐標系與北天東坐標系之間的關系如圖3所示。

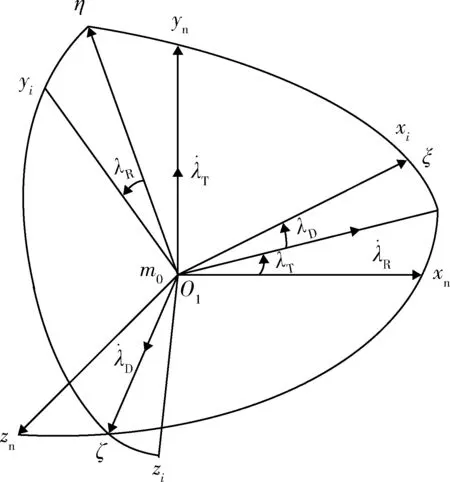
圖3 北天東、視線與攔截坐標系關系圖Fig.3 Geometric relationship of north sky east, sight line and interception coordinate system

在前提假設下，在慣性空間中若tf時刻滿足式(2)或式(3)之一，則說明tf時刻突防飛行器位于KKV可攔截區域之外，即成功突防。

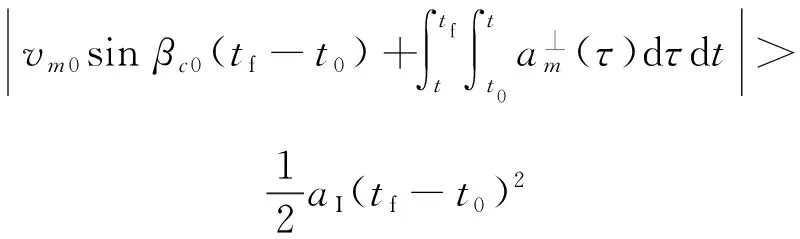
(2)

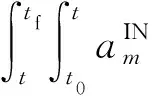
(3)

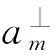
式(2)和式(3)分別代表了在垂直于初始攔截平面方向上突防和在初始攔截平面內突防，下面分別討論。

1.3 垂直于初始攔截平面突防可行性分析

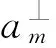
表2 不同參數下突破KKV攔截的可能性

1.4 初始攔截平面內突防可行性分析

同理分析在初始攔截平面內突防可行性。令

ΔvIN=vm0cosβc0sinαcm0-vi0sinαci0.

(4)

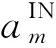
綜上所述，當KKV攔截初始條件與理想攔截條件之間偏差大于一定值時，滑翔飛行器可利用自身機動能力實施機動突防。

2 機動突防制導律

初始攔截平面的法向單位向量即攔截坐標系m0yi軸單位向量，在地心坐標系表示為

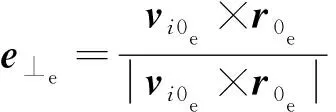
(5)

式中:vi0e=(vxi0e,vyi0e,vzi0e)T為vi0在地心系下的分量；r0e=(rx0e,ry0e,rz0e)T為m0i0在地心系下的分量。

將其轉換到t0時刻的視線坐標系，得

e⊥s=SN(t0)NE(t0)e⊥e,

(6)

式中:NE(t0)為t0時刻地心坐標系到北天東坐標系的轉換矩陣；SN(t0)為t0時刻北天東坐標系到視線坐標系的轉換矩陣；e⊥s=(e⊥ξ,e⊥η,e⊥ζ)T。

則攔截坐標系到t0時刻視線坐標系的轉換矩陣為

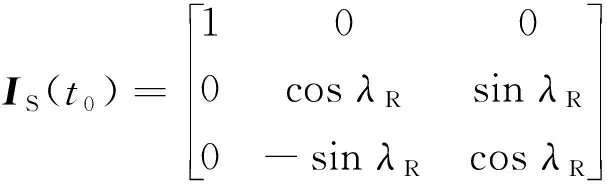
(7)

vm0在攔截坐標系下的投影為

vm0i=IS(t0)SN(t0)NE(t0)vm0e,

(8)

式中:vm0e為vm0在地心坐標系下的向量表示，vm0e=(vxm0e,vym0e,vzm0e)T；vm0i為vm0在攔截坐標系下的向量表示，vm0i=(vxm0i,vym0i,vzm0i)T。

則

(9)

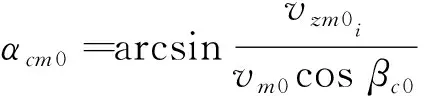
(10)

vi0在攔截坐標系下投影為

vi0i=IS(t0)SN(t0)NE(t0)vi0e,

(11)

式中：vi0e為vi0在地心坐標系下的向量表示，vi0e=(vxi0e,vyi0e,vzi0e)T；vi0i為vi0在攔截坐標系下的向量表示，vi0i=(vxi0i,vyi0i,vzi0i)T。

則

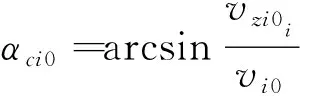
(12)

任意t時刻突防飛行器氣動加速度在攔截坐標系下的投影為

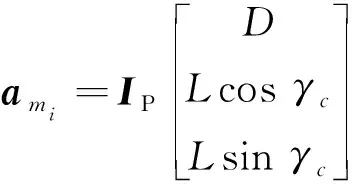
(13)

式中:IP=(Iij),i=1,2,3,j=1,2,3為軌跡坐標系到攔截坐標系的轉換矩陣；IP=IS(t0)SN(t0)NE(t0)·EN(t)NP(t)，其中NP(t)為t時刻軌跡坐標系到北天東坐標系的轉換矩陣，EN(t)為t時刻北天東坐標系到地心坐標系的轉換矩陣。由于攔截坐標系指向t0時刻慣性空間固定方向，因此需要以地心坐標系作為中介，進行向量投影變換。

則ami在攔截坐標系m0yi和m0zi軸上的投影為

(14)

式(14)可進一步化為

(15)

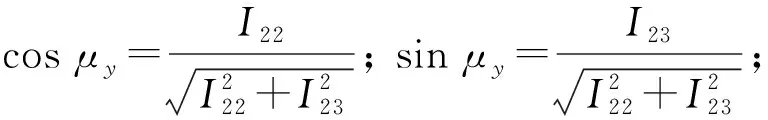
若t時刻滑翔飛行器速度矢量vm與攔截平面的夾角為βc(t)，與m0xiyi平面的夾角為αcm(t)，則由圖2可以看出

(16)

式中:L⊥為在攔截平面垂直方向上的升力分量；LIN為在攔截平面內的升力分量。

由于攔截過程中βc(t),αcm(t)始終為小量，且滑翔飛行器為大升阻比飛行器，因此

(17)

對比式(15)，得

(18)

為了逃脫KKV攔截范圍，應使突防飛行器在攔截坐標系m0yi或m0zi方向上位移最大。即aymi或azmi最大，并且aymi與azmi的方向應與在m0yi或m0zi方向上初始相對速度一致。得到突防制導律為

(19)

式中:αmax為最大攻角。

3 仿真結果及分析

假設滑翔飛行器跟蹤某條預定軌跡飛行，初始飛行高度60 km、速度6 500 m/s、當地速度傾角為0，采用加熱量最小軌跡優化[10]得到，動力學及制導模型參照文獻[11-13]，當飛行至1 200 s時發現助推分離時刻的KKV攔截，KKV距離滑翔飛行器100 km，KKV初始速度為3 000 m/s，并且λD=Θ，λT=Ψ，λR=0，βc0=0，αic0=0，αmc0=3，滑翔飛行器最大攻角取15°，KKV法向和側向最大機動加速度均為40 m/s2，KKV采用經典比例導引[14]。

突防起始時刻(1 200 s)時滑翔飛行器飛行狀態如表3所示，滑翔飛行器氣動參數參照文獻[15]。

表3 飛行器突防起始時刻狀態

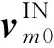
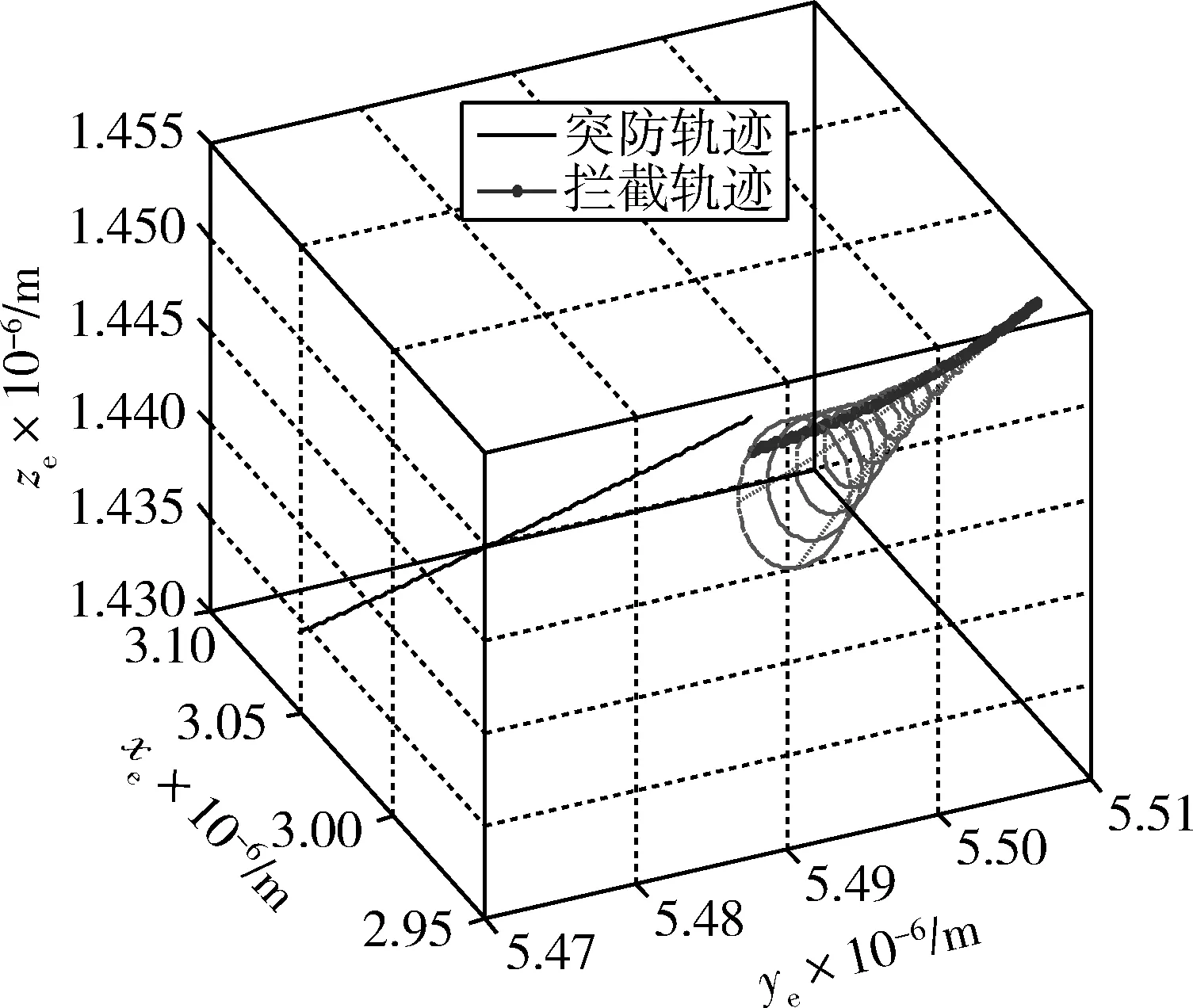
圖4 地心坐標系突防-攔截軌跡Fig.4 Penetration track vs. interception track in geocentric coordinate

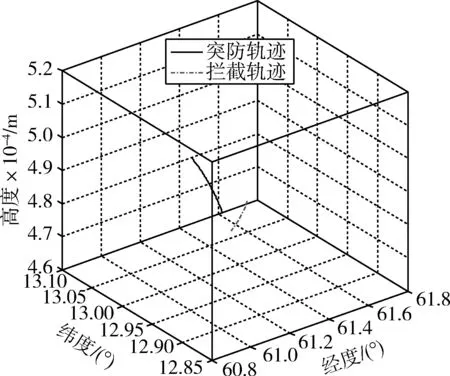
圖5 突防-攔截空間軌跡Fig.5 Penetrating track vs. interception track on earth

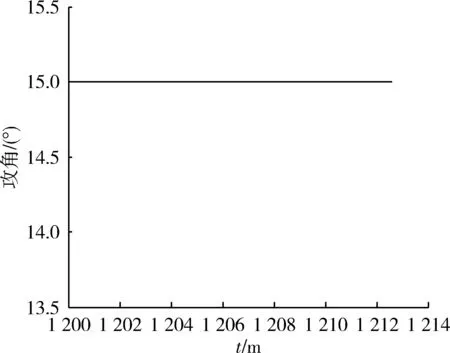
圖6 突防時段攻角變化Fig.6 Angle of attack in penetration period

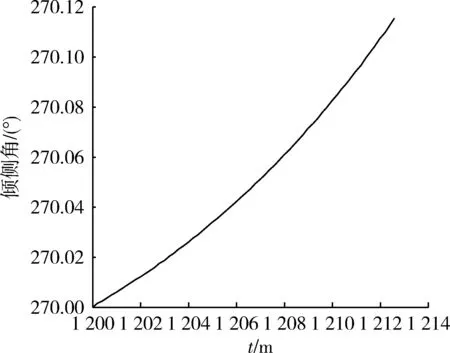
圖7 突防時段傾側角變化Fig.7 Angle of steer in penetration period

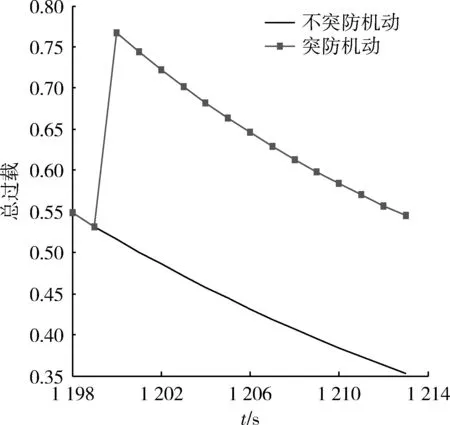
圖8 突防時段總過載變化規律Fig.8 General overload in penetration period

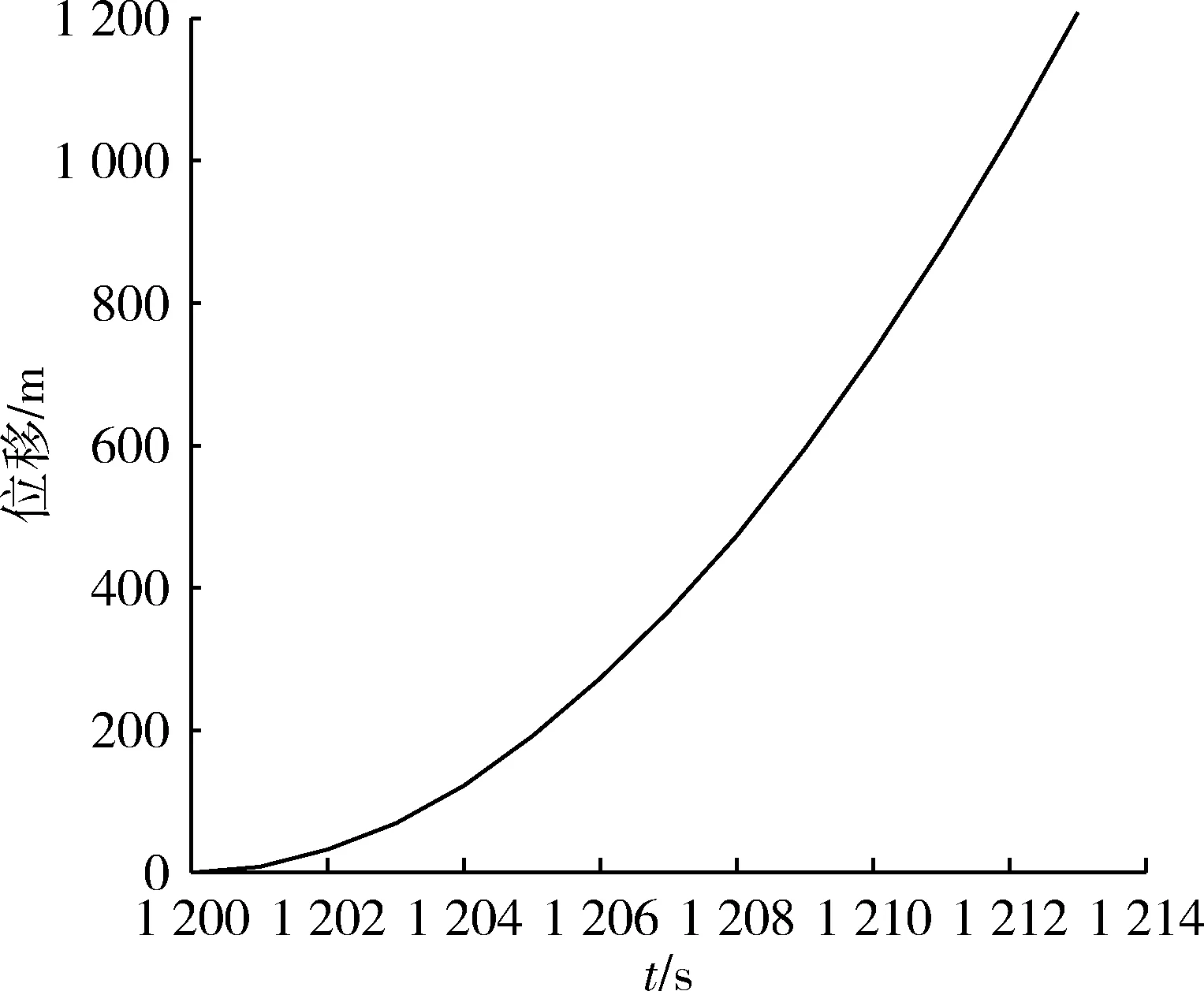
圖9 突防時段位移變化規律(相對于不突防機動軌跡)Fig.9 Displacement in penetration period relative to nonmaneuvering track

由于攔截時間為12.6 s，根據式(1)得KKV在攔截交會時刻的最大機動半徑為4 489.73 m，由于其初速度位于視線方向，說明其在攔截交會時刻偏離初始視線最大距離也為4 489.73 m。假設突防飛行器做勻速運動，其在攔截交會時刻垂直于初始視線方向的位移為

S=vm0sinαmc0(tf-t0)=

5 018.98×sin(3°)×12.6=

3 309.68<4 489.73.

顯然，滑翔飛行器若不作機動突防動作，不能夠逃逸KKV攔截區域，而采用本文設計突防制導律卻實現了逃逸，說明本文反逆軌攔截突防制導律是有效的。

4 結束語

本文對高超聲速飛行器利用空氣動力突破KKV攔截的可能性進行了分析，并根據KKV助推分離時刻狀態推導了突防制導律，利用KKV攔截初始誤差實現了對KKV機動攔截范圍的逃逸。仿真結果表明該方法在KKV攔截初始條件與理想攔截條件存在一定的偏差時，能夠有效逃逸KKV機動攔截范圍。