高重頻脈沖對被動導引頭前端的干擾機理研究

南昊，彭世蕤，王曉燕，許正強

(1.空軍預警學院，湖北 武漢 430019；2.空軍軍務信息中心，北京 100843)

0 引言

在現代戰爭中，以被動導引頭為關鍵部件的反輻射武器成為雷達的主要威脅。近年來，一些新的被動導引頭抗干擾技術的出現，使得對抗反輻射武器更加困難[1-5]。隨著被動導引頭在電磁戰場上發揮的作用日益凸顯，研究對其的干擾技術對提高雷達電子防御能力非常重要。

隨著脈沖技術的發展，采用高重頻脈沖信號對抗接收機的研究逐漸展開，文獻[6]給出了高重頻脈沖對雷達接收機的壓制式干擾試驗效果，文獻[7-10]分析了高重頻激光對激光導引頭的干擾機理，提出干擾效果對信號重復頻率有一定要求。因而高重頻脈沖干擾對信號處理能力較弱的被動導引頭的干擾效果更好，即使在干擾信號脈沖密度處于導引頭處理能力范圍內的情況下，高重頻干擾同樣可發揮作用。為此，本文對高重頻脈沖進入導引頭前端的響應情況進行理論研究，明確了高重頻干擾對前端的作用機理及干擾效能與脈沖參數之間的理論關系。

1 高重頻脈沖信號特征

高重頻脈沖信號是一種重復頻率極高的脈沖信號，脈沖寬度通常為幾納秒至幾百納秒，遠小于雷達發射信號的脈沖寬度，具有超寬帶的特性。其時域表達式為[11]

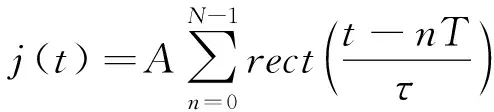
(1)

式中：A為脈沖幅度；τ為脈沖寬度；T為脈沖重復周期；N為脈沖數量；rect(·)為矩形函數。

將式(1)進行傅里葉變換得到高重頻脈沖的頻域表達式為

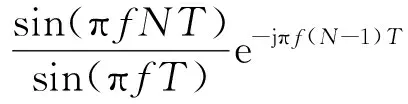
(2)

設PRFj為高重頻干擾脈沖重復頻率，當A=2 mV，τ=1 ns，N=1 000，PRFj=200 kHz時，高重頻脈沖時域波形和頻譜如圖1所示。……