隨商的訂購-定價聯合決策問題

吉清凱,胡祥培,郭 強,趙 達

(1.海南大學經濟與管理學院,海南 海口 570228；2.東南大學經濟管理學院，江蘇 南京 211189；3.大連理工大學管理與經濟學部,遼寧 大連 116024；4.海南大學科研處，海南 海口 570228)

1 引言

供應鏈運作面臨許多風險，除了常見的隨機需求風險外，隨機供應的風險也越來越突顯。據著名咨詢公司McKinsey與Accenture近年的調查，對眾多制造企業而言，供應風險管理已成頭等大事，許多企業甚至認為供應穩定性比成本控制還要重要[1]。因此，隨機供應與隨機需求條件下的供應鏈管理已成為業界與學術界共同關注的熱點。其中，隨機供需條件下的訂購-定價決策模型是供應鏈管理領域的前沿研究方向之一，近年在國內外頂級期刊及會議上時有相關的論文發表。對于許多生產創新型消費類電子產品(Innovative Consumer Electronics，ICE，如智能手機)的裝配式制造企業而言，隨機供應更加常見，同時，在零部件互配性的作用下，隨機供應的風險將被放大。并且，因為ICE產品具有生產周期長、生命周期短、熱銷周期短和需求不穩定的特點，所以訂購與定價是這類裝配商的生死攸關的決策，如何在隨機供應與隨機需求的條件下協調訂購與定價從而使得供需匹配是其迫待解決的難題。在這一背景下，隨機供需條件下裝配商訂購-定價的決策模型研究具有重要的理論意義與實際意義。

ICE產品往往由成百上千種零部件組成，其中涉及諸多新技術、新設計與新工藝，在生產制造過程中將不可避免地遇到諸如次品率過高、特殊材料不足、精密設備出錯等許多麻煩，零部件供應商的產能因此表現出隨機性，從而導致零部件與最終產品供應的隨機性。例如，蘋果手機iPhone 5曾因為其屏幕供應商在生產in-cell觸控屏時遇到麻煩而出現缺貨，HTC One Mini也曾因機殼短缺導致新品發布大幅延遲而錯失銷售良機。對于隨機供應風險，裝配商不愿用囤積庫存來應對，畢竟在高新制造行業中庫存呆滯的風險更高，尤其是ICE產品中包含許多不通用、易過時的零部件，呆滯庫存意味著極大的沉沒成本。因此，裝配商更多地寄望于科學的零部件訂購決策與產品定價決策來平衡供需。但當需求與供應都具有隨機性時，定價與訂購的關系變得復雜。盡管已有不少研究考慮了需求或供應隨機情況下的訂購與定價模型[2]，但其并不能完全適用于生產ICE產品的裝配系統，仍存在有待改進之處：如以往有些研究比較局限地考慮包含兩種零部件的系統，或者只假設某一個零部件的供應具有隨機性[3]；又或者預先假設訂購策略的結構而尋找最優參數[4]，對于訂購與定價的最優決策本身的刻畫不夠充分等等。因此，目前仍需在前人的基礎上，針對隨機供需下一般化的裝配系統(指包含n種零部件，且每一零部件的供應都具有隨機性)，為其中的多零部件訂購決策、組裝決策及最終產品定價決策建立相應的模型，刻畫其最優的訂購-定價策略，為裝配商的管理實踐提供科學的決策支持。由于本文所研究的裝配系統具有多重隨機性與零部件互配性，這將使得n種零部件訂購量間的最優比例關系變得不清楚，零部件訂購量與最終產品定價的交互影響也變得復雜。

針對上述難題，本文建立關于零部件訂購與最終產品定價的隨機非線性約束規劃模型，根據系統特性降低模型的維度，然后綜合利用分解法、逆推法與約束極值的處理方法刻畫出最優的訂購策略與定價策略，并對隨機供應與需求的影響展開分析，為裝配商提供科學的輔助決策工具與有益的管理啟示。

與本文相關的文獻主要有兩類：(1)生產-定價或訂購-定價聯合優化模型，(2)隨機供需下的生產或訂購決策模型。第一類研究始于Whitin[5]，其刻畫了均勻分布需求下的最優生產/訂購與產價的聯合決策，后來眾多學者對一般分布情況下的最優決策進行了細致的刻畫[6]，并從多種角度(系統特征與產品特性等)做了大量的擴展研究[7]：如李貴萍[8]基于前景理論進行研究報童定價-訂購決策；段永瑞等[9]研究有限時域內部分缺貨的變質品生產與定價聯合決策，Yan Xiaoming與Wang Yong[10]研究隨機產出下易逝品的訂購-定價決策；Pan Wenting與So[3]研究包含兩個零部件的系統，假設某個零部件具有隨機產出，刻畫訂購-定價最優策略，等等。在第二類研究中，學者們著力刻畫隨機供需下各類系統的最優生產/訂購策略，如Wang Yunzheng與Gerchak[11]研究同時存在不確定產能與隨機產出時的單級系統，證明最優策略具有一種單臨界點的結構；Hwang與Singh[12]研究各級產能都不確定且具有固定成本的多級串行系統，證明單周期中的最優策略是一種環環相扣的二臨界值型策略；Hu Xinxin等[13]研究包含兩個生產基地的分布式系統，刻畫了最優的庫存分配策略與生產策略；Erdem等[14]研究面對多個具有不確定產能的供應商的EOQ系統；Ji Qingkai等[15]刻畫了隨機供需下一般裝配系統的最優生產策略；等等。還有學者假設系統按基本庫存策略運行，尋求隨機供需下最優的策略參數并考察系統的表現：如Bollapragada等[4]研究具有服務水平約束的裝配系統，分析了最優服務水平與最優策略參數；Bollapragada等[16]通過數值分析研究不確定產能與提前期在一個實際的裝配系統中的影響。此外，也有學者考慮各種針對隨機供應的應對策略，如Wang Yimin等[17]比較了雙源采購與流程改進(可隨機地提高產能)的優劣，錢佳與駱建文[18]假設零售商面對的是具有不確定產能的主要供應商與產能充沛的后備供應商，研究訂購量的分配以及對主要供應商的支持投入(如流程改進與知識輸入等)決策；馬士華與李毅鵬[19]建立信息共享或加班趕工及資源外包下多供應商間的橫向協同模型；Xiao Yongbo等[20]研究裝配系統中包含預先裝配量、零部件預存量、追加裝配量以及外包量的多階段決策模型。

盡管第一類研究已經從多種不同的角度對生產/訂購與定價的聯合優化進行了大量研究，但是其中涉及的生產/庫存系統主要是單級或串行系統，與本文中的裝配系統在結構上有本質不同。在裝配系統中要考慮多個零部件的匹配，隨機供需下的訂購-定價聯合決策將變得更加困難，Pan Wenting與So[3]做了初步的探索，但在模型通用性方面仍有較大的改進空間。第二類研究中關于裝配系統的研究有四篇，它們與本研究的不同之處在于：Bollapragada等[4]關注的是某種庫存控制策略的最優參數，Bollapragada等[16]用純數值分析的方法研究提前期對裝配系統的影響，而本文聚焦于建立解析模型、刻畫最優的訂購-定價聯合決策；Xiao Yongbo等[20]關注的是組裝產能不確定下兩階段的生產與外包決策，而本文是在Ji Qingkai等[15]的基礎上，研究零部件產能不確定和最終產品需求隨機條件下單階段內裝配商的零部件訂購量與最終產品定價聯合決策。綜上所述，本研究將有助于豐富訂購-定價聯合優化與隨機環境下裝配系統運作管理領域的理論研究，且有助于管理者在隨機環境下做出科學的訂購與定價決策。

2 問題描述與假設

一個裝配商在銷售季前分別從n個供應商處購買n種零部件組裝成一種產品進行出售，每一單位產品包含一單位的零部件i，i=1…,n。假設產品的隨機需求依賴于產品價格p，記為D(p,)=y(p)，其中y(p)是關于p的單調減函數，是獨立于p的隨機變量，代表市場的隨機擾動。令φ(·)與Φ(·)分別表示的概率分布函數與累積分布函數，令而表示失敗率或故障率(Hazard Rate)函數。假設定義在支撐集[B,C]上，C>B≥0，若E()=1，則y(p)是需求的期望值。由于原料不足、生產工藝不精導致停機與返工等原因，零部件i=1…,n的產能Ki為隨機變量，其累積分布函數與概率分布函數分別為Fi(·)與fi(·)，支撐集為(0,)。Ki(i=1…,n) 相互獨立，假設裝配商掌握每個供應商的產能信息。令ui表示裝配商對零部件i的訂購量，記u=(u1,…,un)。令wi為零部件i的批發單價，ci為生產成本，ciui時，故供應商i的最優計劃產量而當qi≤ui時，所以因此，裝配商訂購ui單位的零部件i，但它實際收到的供應量為min{ui,Ki}。

表1 主要變量和參數符號說明

為便于分析，另做如下假設：

(A1)零部件與最終產品都不具有殘值，其庫存成本亦可忽略；

(A2)組裝成本為零，或可認為其已從p中扣除；

(A3)若產出無法滿足市場需求，則裝配商僅承受相應的銷售損失，而不存在額外的缺貨懲罰成本；

(A4)裝配商是區域性的壟斷者，其零部件購買價wi,i=1…,n為外生變量。

事件發生順序為：

(1)裝配商對訂購量u與產品價格p做出決策；

(2)供應商i根據計劃其產量并進行生產配送；

(3)裝配商收到零部件的實際供應量；

(4)匹配零部件組裝成產品并滿足需求。

因此，裝配商的期望利潤函數為

Π(u,p)=E[pmin{min{u1,K1},…,min{un,Kn},D(p,)

(1)

其中E表示關于Ki，i=1…,n的期望。裝配商的目標是最大化其期望利潤。

3 模型分析

當供應確定時，顯然裝配商應訂購等量的零部件，否則因零部件不匹配只會徒增成本。在隨機供應下，是否每個零部件的訂購量仍應保持相等？引理1回答這一關鍵問題。

證明不失一般性，假設u1≤…≤un(否則重新編號)，則此時裝配商的期望函數變為

Π(u,p)=E[pmin{u1,K1,…,Kn,

(2)

引理1說明：盡管產能不確定性可能導致各零部件的實際供應量不相匹配，但其訂購量仍應保持匹配。其根本原因在于訂購量不會對產能有影響，裝配商所應做的就是按等比例訂購，否則零部件供應量不匹配的可能性會更大。根據引理1，可用單一變量u表示裝配商的訂購量，則其期望利潤函數可簡寫為

Π(u,p)=E[pmin{u,K,D(p,)

(3)

注意到當不存在任何供應能力約束時，裝配商的問題退化為一個經典報童框架下的訂購-定價模型[21]，如Petruzzi與Dada[21]中所用的方法，可定義z=u/y(p)為所謂的“庫存因子”(Stocking Factor)，從而能夠將訂購決策u與p從E[min{u,y(p)}]這一復雜的關系中分離出來，有利于分析并最終刻畫出最優的訂購與定價決策。但在本章中，如(3)式所示，隨機供應K的存在使得這一技巧不再適用，最優解的刻畫變得更加困難。因此，下面分別求解給定任一可行價格與訂購量時，相應的最優訂購量與最優價格。

3.1 任一可行價格對應的最優訂購量

(4)

或，等價地，

(5)

的唯一且有限的解。

證明將(3)式展開得:

對其求偏導有

u*(p)為一階條件?Π(u,p)/?u=0的解。因

根據式(4)，利用隱函數求導法則，可得:

其中分子中第一項為正，第二項為負，du*(p)/dp的符號難以判定，可見隨機需求下的最優訂購量與價格的關系相當復雜。下面給出在特定條件下最優訂購量與價格的單調關系。

為供應量為u時供不應求的概率關于價格p的彈性[22]。

性質1當ξ(u*(p),p)≥1時，du*(p)/dp≤0，即最優訂購量是價格的減函數。

證明因為ξ(u*(p),p)≥1等價于

根據以上兩個不等式，可判定du*(p)/dp≤0。

ξ(u*(p),p)≥1的含義是：假設裝配商擁有u*(p)件產品，若價格增大一個百分比，則出現供不應求的概率就降低超過一個百分比，因此價格上升時裝配商應適當減少訂購。此時，盡管隨機供應的存在會使收貨量隨機地比訂購量少，但裝配商在訂購時仍應適當減少訂購量，否則收貨量有可能高于裝配商所需要的，反而出現供過于求的情況。

性質2 最優訂購量u*(p)隨著需求隨機增大(即隨機增大)而增大，隨著零部件產能(Ki，i=1…,n)隨機增大而增大。

3.2 任一訂購量對應的最優價格

對于任一零部件訂購量，其對應的最優價格如以下命題所示。

E[min{u,K,

證明對Π(u,p)求偏導有:

記

其代表銷售量對價格的反應，再令

因此有

由性質1與性質3可見，在隨機供需下，Π(u,p)不一定是次模函數，價格決策與訂購決策不一定具有可替代性，調高價格不一定意味著要減少訂購量，而增加訂購量不一定意味著要調低價格。但在一般情況下(指ξ(u,p)滿足遞增性[22])，性質1與性質3中的結論仍成立。

3.3 最優訂購-定價聯合決策

上兩節已經分別刻畫給定價格p時的最優訂購量u*(p)與給定訂購量u時的最優價格p*(u)，但u*(p)與p*(u)只分別代表函數Π(u,p)的兩條最優路徑，聯合最優解(u*,p*)仍未得知。因為u*(p)比p*(u)具有更為簡單的形式，故本文沿著u*(p)這一最優路徑尋找聯合最優解。將u*(p)代入Π(u,p)，則裝配商的問題變為：

對Π(u*(p),p)求導有：

其中，第二個等號的得出用到了u*(p)的最優性，即?Π(u*(p),p)/?u=0。對dΠ(u*(p),p)/dp再求導有：

若同樣假設py(p)為關于p的凹函數，則上式中后兩項均為負，但第一項等價于

其為正項，故難以判斷d2Π(u*(p),p)/dp2的符號，從而不能對dΠ(u*(p),p)/dp=0的解的唯一性下定論。但是，可根據以上分析得到如下命題。

命題3 最優訂購-定價聯合決策(u*,p*)滿足以下條件：

(6)

與式(6)中的第二個等式矛盾。

4 數值實驗：隨機供需的影響

在大量的數值實驗中，上一章中已被嚴格證明的理論結論均得到驗證，在此章不再贅述。本章的目的是通過數值實驗來進一步直觀地考察隨機供需對最優訂購與定價的影響。考慮n=2的裝配系統，零部件批發價為w1=10。同樣只考慮β>1即彈性需求的情況。需求隨機因素不依賴于價格，并且服從均值為1的正態分布，即～N(1,σ)，1?σ>0表示方差較均值小得多，從而取負值的概率幾乎為零。此時E[D(p,)]=αp-β，代表裝配商對需求的預測。令α=100，在以下算例中令β在{1.1,1.5,2.0}內變動以考察需求價格彈性的影響。

假設各零部件供應商的隨機產能均服從Weibull分布，即Ki～Weibull(λi,κi)，i=1,2，κi∈+，λi>0，Ki的支撐集為[0,∞)。Ki的均值為λiΓ(1+1/κi)，方差為分布是可靠性工程領域常用的分布，用以描述一個系統或部件在某段時間內正常運行的能力。若用Weibull分布來描述關于“失敗-時間”的變量，則其隱含著失敗率與時間的冪數成比例關系，并且當形狀參數κi>1時，表明失敗率隨時間遞增。因為產能在很大程度上決定于生產制造系統的可靠性或失敗率，所以用Weibull分布來刻畫隨機產能比較貼切。Weibull分布的概率密度函數嚴重依賴于形狀參數κi，當κi較大時其概率密度函數具有單峰形狀，可表明隨機產能在單峰(代表最初的設計產能)的周圍波動，比較符合實際情況。因此，在以下算例中，令κi=5，i=1,2(即兩個供應商的初始設計產能相等，或者裝配商從兩個供應商處預訂的產能相等)，只變化尺度參數λi以考察其影響。

(I)需求方差及需求彈性的影響

表2給出需求隨機因素的方差變化而其它參數保持不變時最優解(u*,p*)及最優利潤Π*的取值。其中，λ1=λ2=10，σ以步長0.01在[0.01,0.11]上變動，表格中數值根據寬度四舍五入取有限位小數列出。表中用上下箭頭表示變量的上升與下降的變化趨勢，δ的定義與前相同。

表2 σ變化時(u*,p*)及Π*的取值

觀察發現：保持其它不變，若σ減小，則u*增大、p*減小、Π*增大，而δ的變化依賴于β。換言之，當需求隨機因素的方差變小時，零部件訂購量增大、最終產品價格減小、裝配商獲取的期望利潤增大，但其對裝配商利潤的邊際促進作用依賴于需求彈性。管理啟示：在乘式需求下，需求方差VAR[D(p,)]=[y(p)]2σ，其是關于p的減函數、σ的增函數。當σ減小時，需求方差整體而言會減小，因此，裝配商將降低價格以刺激需求并增加訂購量。盡管裝配商降低價格使得需求方差有增大的趨勢，但總體而言，仍是隨σ減小的表示對應σ的最優價格)，這保證了裝配商利潤隨σ增大。在現實中，隨著電子商務的盛行，越來越多創新型消費類電子產品廠商在網絡上銷售產品，并且它們往往為其即將推出的新產品策劃預售或預訂(Advance Selling/Booking，或Presale)的活動，盡管對于這種活動存在許多營銷學上的解釋，但其對于降低需求方差其實有一定的作用。這是因為預售/訂能夠預先鎖定部分需求，并且通過網站數據統計能夠進一步修正需求預測，降低需求估計的偏差。有些智能手機廠商在預售/訂后降低價格(產品仍在熱賣季度中)，盡管這種行為背后的原因可能包括價格競爭、產品關注度下降等等，但需求方差的下降或許是廠商降價的重要原因之一。

(II)產能均值與方差的交叉影響

圖1給出零部件i的產能分布參數以步長1在[1,21]上變化而其它參數保持不變時最優解(u*,p*)及最優利潤Π*的取值。其中，λ3-i=10，實線對應λ1固定而λ2變化時參數的取值，虛線對應λ2固定而λ1變化時參數的取值。

觀察發現：對于i=1,2，保持λ3-i=10和其它參數不變，若λi增大，則u*增大、p*減小、Π*增大。并且，對比“λ1增大λ2不變”與“λ2增大λ1不變”兩種情況發現，前者中的u*比后者中的小，而兩種情況下的p*、Π*幾乎一致。

圖1 λ3-i=10而λi變化時u*、p*和Π*的取值

管理啟示：當λi變大時，期望產能變大，但產能也變得越來越不穩定。λi的增大可以解釋為零部件供應商i將其業務再外包給多個二級供應商。此時，總體而言，零部件i的產能(供應量)均值變大了，裝配商能夠增加訂購量、降低產品價格并最終獲取更高利潤。但是，二級供應商的增多也使得生產過程中面對的風險更大，從而導致零部件i的產能(供應量)變得越來越不穩定。對裝配商而言，當供應商i之下的二級供應商數量逐漸增大時，零部件i的產能均值增大的好處逐漸被其產能方差增大的風險抵消，裝配商能獲得的利潤增額越來越小。因此，在存在供應風險時，裝配商有必要加強對二級供應商的管理。現實中許多裝配商也越來越重視供應鏈的可視性。

以上結果的一個前提條件是λ3-i=10，即零部件3-i的產能相對已經比較充足(E[K3-i]≈9)。當零部件3-i的產能并不充足時(如λ3-i=1)，增大λi將出現極其不同的情況，如圖2所示。

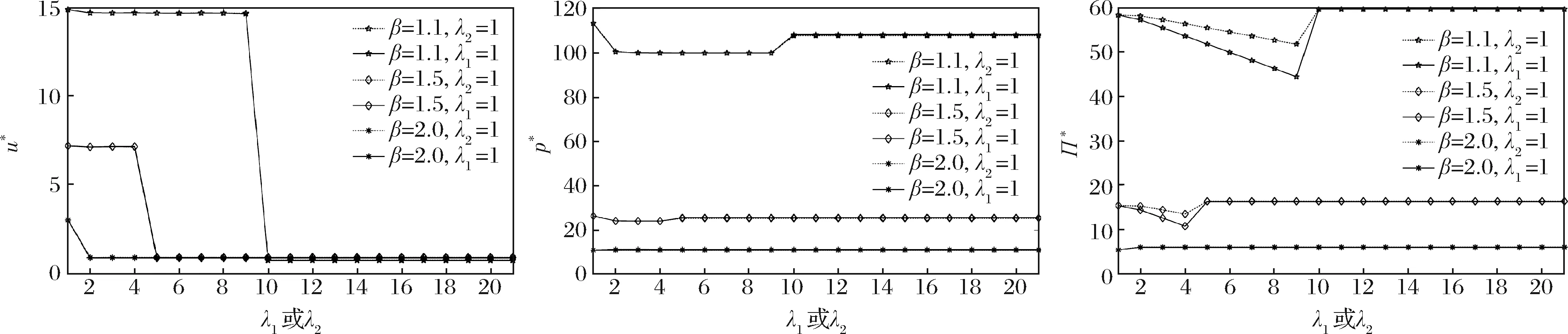
圖2 λ3-i=1而λi變化時u*、p*和Π*的取值

觀察結果：對于i=1,2，保持λ3-i=1和其它參數不變，若λi增大，則u*、p*與Π*非單調地變化。整體而言，u*有減小的趨勢；當需求彈性較小時(β=1.1或β=1.5)，p*先減后增，Π*也先減后增，當彈性較大時(β=2.0)，p*先增后減，而Π*極其微小地增大。并且，對比“λ1增大λ2不變”與“λ2增大λ1不變”兩種情況發現，前者中的Π*比后者中的大，而兩種情況下的u*、p*幾乎一致。當λi增大到某個臨界點后，u*、p*與Π*的變化均趨于平緩。

管理啟示：如前所述，λi的增大可以解釋為零部件供應商i將其業務外包給多個二級供應商。此時，零部件i的產能(供應量)的均值與方差均變大了。但由于零部件3-i的產能并不充足，λi的增大反而使得零部件不相匹配的可能性增大。只有當二級供應商的數量多到一定數目后，即零部件i產能均值增大的好處超過其方差變大的壞處后，裝配商才能夠勉強獲取更高利潤，但增額極小。因此，供應商i的二級供應商數量增大對裝配商而言并不一定有利。另外，當裝配商要鼓勵其零部件供應商發展二級供應商時，它應該鼓勵那些具有產能瓶頸的供應商，否則有可能利潤受損。

5 結語

本文研究隨機供需下裝配商單周期內的零部件訂購與最終產品定價聯合最優化決策模型，求解了給定價格時的最優零部件訂購量和給定訂購量時的最優價格，然后給出關于最優訂購與定價聯合決策的必要條件，最后分析了隨機供需對最優決策的影響。研究發現：盡管存在供需隨機性，裝配商仍應按相等比例訂購零部件，但其訂購與定價決策受供需隨機分布的影響，難以精確協調。最后通過數值分析說明：增大供應產能的均值(如通過投資新的生產線或是激勵供應商加班加點)或減小供應產能的方差(如加強對生產設備的預防性維護、加強對工人的培訓教育以減少操作失誤等)可以使裝配商獲益，且應依大均值、小方差與小差異三個指標進行供應商改進，即不單要提高零部件供應商的產能，還要使其更加穩定，并且要使各個零部件產能盡量匹配。另外，當各供應商供應能力相同時，改進成本較低的供應商對裝配商而言更有利。這些模型結論與數值分析結果能為裝配商的訂購-定價決策以及供應商改進提供有益的借鑒。

本文是在信息對稱的情況下展開研究，將來可考慮供需信息不對稱下的信息甄別以及采購契約菜單的設計。