須條內纖維頭端分布對紡紗牽伸過程的影響

麻寶龍，汪 軍, b

(東華大學 a.紡織學院； b.紡織面料技術教育部重點實驗室，上海 201620)

牽伸是紡紗過程中重要的加工工序，涉及并條、粗紗、細紗等多道紡紗工序，其是將須條單位長度的質量降低到規定要求的重要步驟，對最終的成紗品質有重要影響。Foster等[1-4]推導了須條內纖維的排布形式以及條干不勻的產生原因，提出了著名的牽伸波理論。Goto等[5]隨后在Foster和Grishin[6]的基礎上分析了纖維運動的穩態。Rao[7]建立了比較完整的理想須條結構的數學模型，后人的很多模型中也都采用相同的假設條件。Martindale[8-10]在假設纖維長度和細度是獨立的條件下，提出了被后人廣泛使用的理想紗條“極限不勻”公式，在其基礎上才有了不勻率指數等表征須條不勻率的指標。林倩等[11-13]、嚴廣松等[14-16]和Kuang等[17]則分別建立各自的數學模型，用于研究牽伸工藝參數對紗線不勻的影響。但這些研究未能指出牽伸區內纖維運動狀態的變化情況，以及輸出條干不勻產生的原因。

筆者課題組利用離散理論建立了一個牽伸基礎模型，并分析了輸出條干不勻的影響因素，也驗證了模型的正確性，但也未能對牽伸區內部做更詳細的研究[18]。本文在文獻[18]研究基礎上，細化了牽伸區內纖維的運動行為，建立一個牽伸改進模型，著重研究須條內纖維頭端間隔對輸出條干不勻的影響，指出牽伸過程中條干不勻產生的機理。

1 模型的建立

1.1 牽伸區內纖維的分類

牽伸區內部的纖維，根據其運動狀態和受羅拉控制的情況，可被分為不同的類型。每種類型纖維分布的大致區域范圍如圖1所示，其中，v2為后羅拉表面速度，v1為前羅拉表面速度。

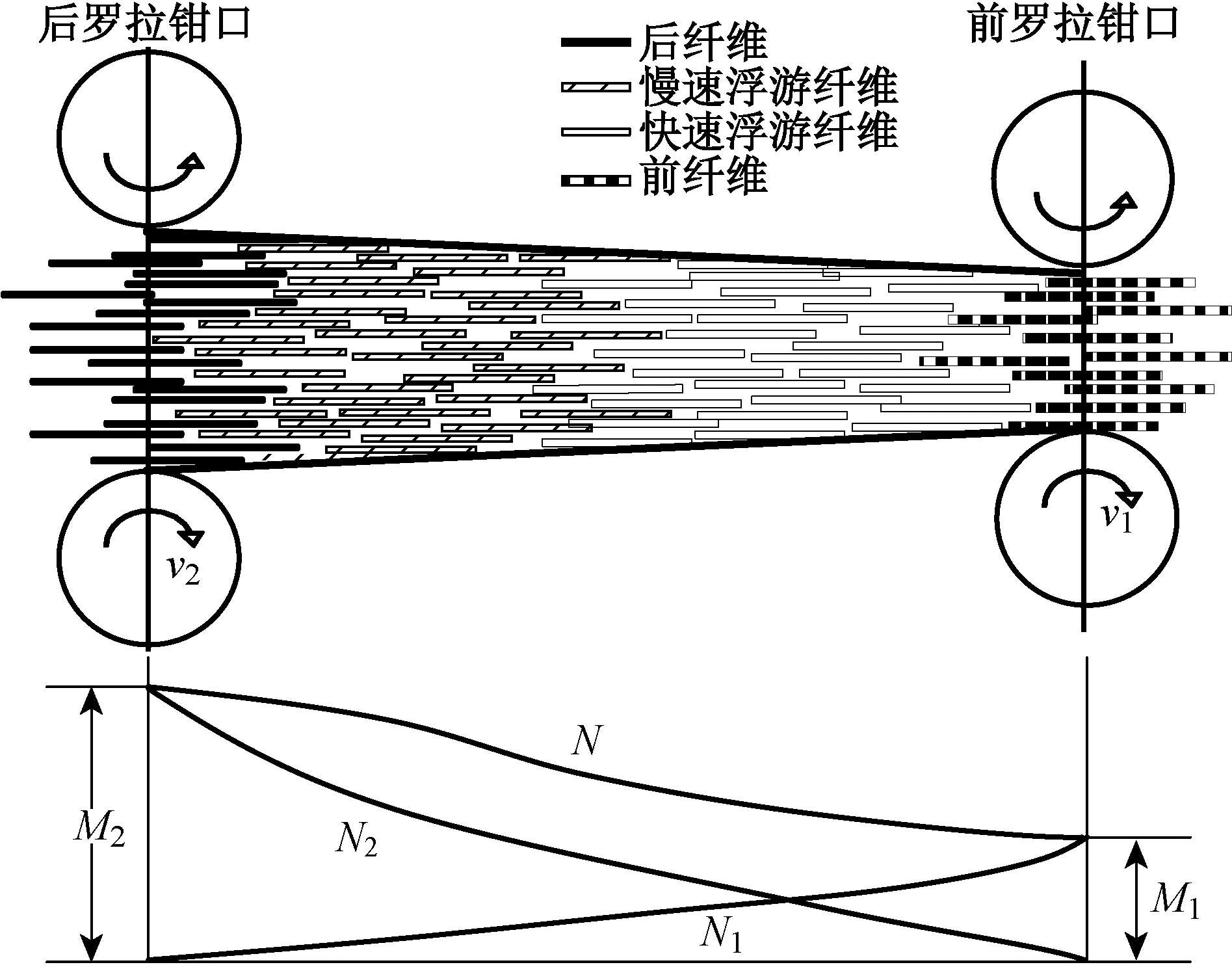
圖1 牽伸區內各類纖維分布示意圖Fig.1 Schematic diagram of fiber distributions in a drafting zone

按纖維運動的速度分類[19]，可將其分為快速纖維(以速度v1運動)和慢速纖維(以速度v2運動)，其數量分別為N1和N2。按纖維受羅拉控制的情況分類[20]，可將牽伸區內的纖維分為前纖維、后纖維和浮游纖維，其數量分別用M1、M2和Mf表示。對浮游纖維而言，根據其運動速度可以進一步細分為慢速浮游纖維和快速浮游纖維，數量分別為Msf和Mff。假設某時刻牽伸區內的纖維總根數為N，有N=N1+N2。根據每種類型纖維間的關系，又有N1=M1+Mff，N2=M2+Msf，Mf=Msf+Mff。

1.2 牽伸改進模型的建立

根據文獻[18]中所提出的建模方法，模型仿真執行中活動實體的數量就是牽伸區內的纖維總根數，利用活動實體的不同狀態變化來模擬牽伸區內纖維狀態的改變，統計某種狀態下活動實體的數據就可以獲得某類型纖維的分布情況。本文的建模參數與牽伸基礎模型相同，主要有6個輸入參數:L為纖維長度，mm；P為牽伸區內纖維變速點位置與前鉗口的距離，mm；S為輸入須條線密度，g/m；R為羅拉中心距，mm；后羅拉速度v2和前羅拉速度v1，m/min。

單根纖維運動狀態變化如圖2所示。由圖2可知，每根纖維從輸入牽伸區內(Ⅰ)開始，其運動狀態會經歷4次變化(Ⅱ～Ⅴ): 進入牽伸區內先受到后羅拉控制(Ⅱ)，當脫離后羅拉控制時變成慢速浮游纖維(Ⅲ)，被加速后轉變為快速浮游纖維(Ⅳ)，最終受前羅拉控制成為前纖維從牽伸區輸出(Ⅴ)。以模型中一個活動實體為例，其狀態只會在某些離散的時間點上瞬時改變，這些時間點就是事件的發生點，其中事件被定義為可能改變系統狀態的瞬時發生的行為[21]。

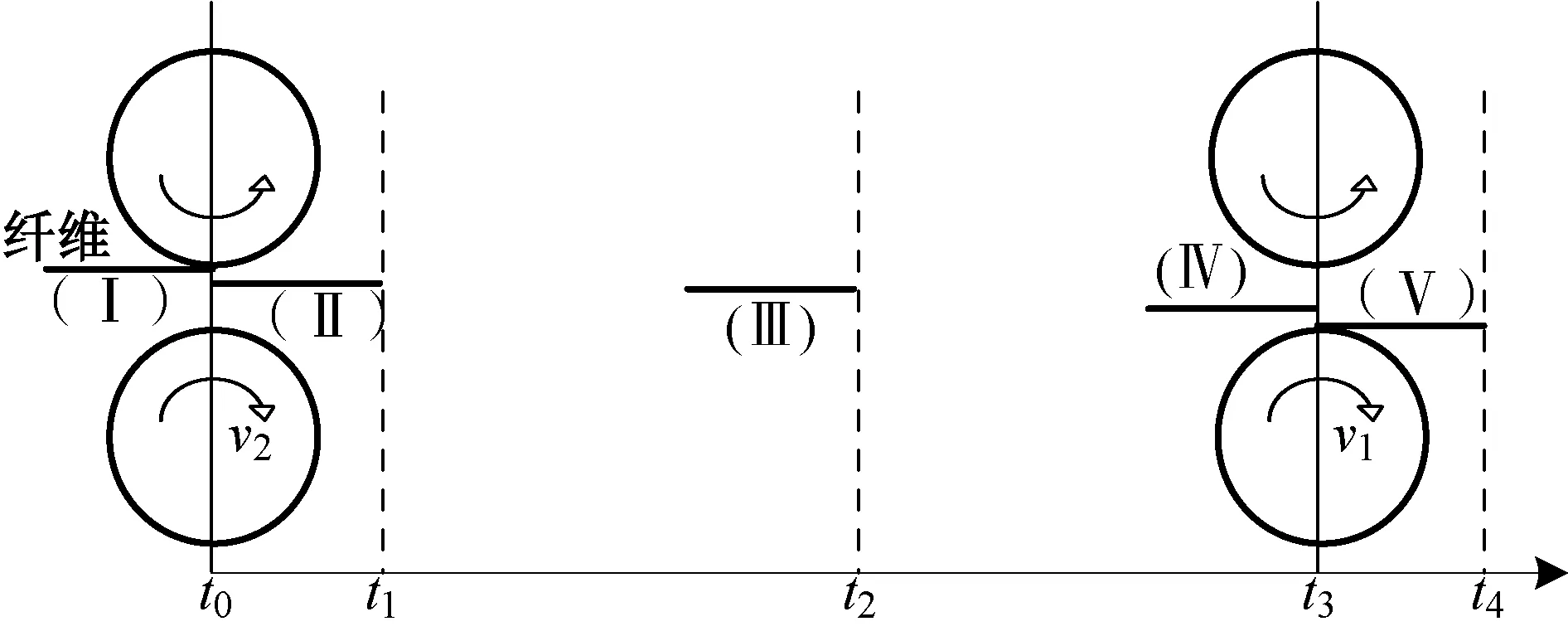
圖2 單根纖維運動狀態變化Fig.2 Behavior of a separate fiber

圖2中以一個活動實體為例，即某一根纖維，在橫坐標上注明了該活動實體將要被離散事件改變狀態的時刻點，其中的t0到t4時刻即為纖維運動狀態發生變化的時刻。該模型的仿真流程圖如圖3所示。

(1)當纖維的頭端被后羅拉握持，即纖維進入牽伸區的過程(Ⅰ)，由模塊“GENERATE 1”實現。該模塊用于不斷地產生活動實體，相鄰兩個活動實體間隔的平均時間為T，其計算方法與文獻[18]相同。如果系統在t0時刻產生一個活動實體，則該活動實體要經歷的離散隨機事件及其仿真過程如(2)～(5)所述。

(2)模塊“ADVANCE 1”用于仿真活動實體從t0到t1時刻的狀態，此階段(Ⅱ)的纖維運動一直在后羅拉強控制之下，屬于后纖維。其時間跨度的計算公式為

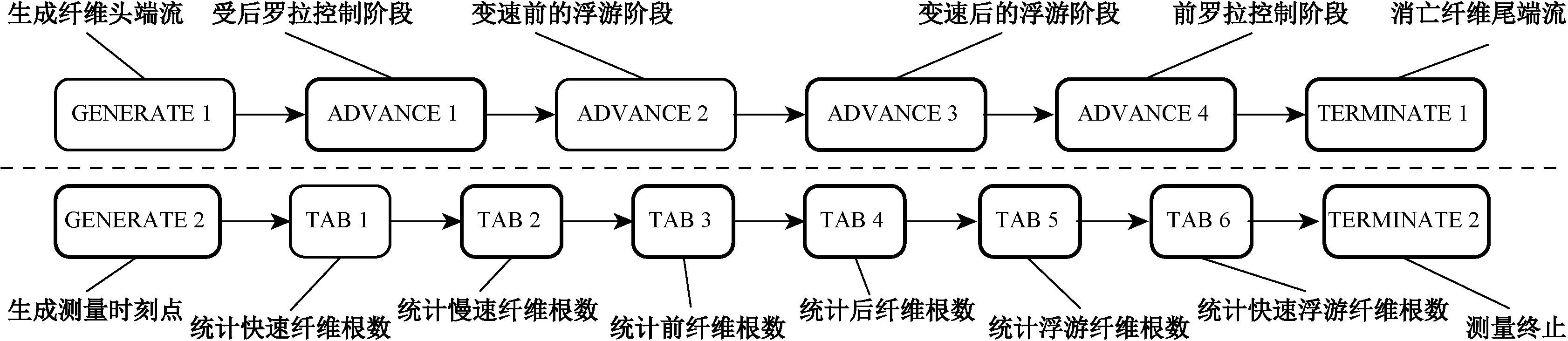
圖3 牽伸改進模型的仿真流程圖Fig.3 Flow chart of simulation of improved drafting model

(1)

式中:LBN為纖維被握持的長度，即后羅拉強控制區域的長度，根據羅拉加壓以及摩擦力界的形式，調整其數值大小變化。在t1時刻，活動實體的狀態發生第一次變化，模擬纖維從后纖維轉變為慢速浮游纖維，此時纖維的尾端脫離后羅拉控制，變成“浮游”的狀態，但仍保持慢速運動。

(3)模塊“ADVANCE 2”用于仿真活動實體從t1到t2時刻的狀態，此階段(Ⅲ)的纖維運動不受羅拉控制，但也沒有被加速。這段時間大小為

(2)

(3)

(4)模塊“ADVANCE 3”用于仿真活動實體從t2到t3時刻的狀態，此階段(Ⅳ)的纖維運動依然不受羅拉控制，但已被加速到v1。這個狀態持續時間的計算公式為

(4)

在t3時刻，活動實體的狀態發生第三次變化，模擬纖維轉變為前纖維。此時纖維的頭端到達前鉗口處，受到前羅拉的握持作用。

(5)模塊“ADVANCE 4”用于仿真活動實體從t3到t4時刻的狀態，此階段(Ⅴ)的纖維運動一直在前羅拉的強控制之下。很顯然，這段時間的長度同樣取決于羅拉強控制范圍的大小，其計算公式為

(5)

式中:LFN為前羅拉強控制區域的長度。在t4時刻，纖維的尾端脫離前羅拉控制，移出牽伸區，意味著該根纖維的牽伸過程結束。模塊“TERMINATE 1”用于仿真這個時刻，將該活動實體消亡，結束該活動實體的仿真過程。

在圖3中，采用統計模塊來輸出模型的仿真結果。其中，模塊“GENERATE 2”用于控制數據統計的時間間隔，從模塊“TAB 1”到“TAB 6”用于讀取整個牽伸區內或某個截面上不同類型纖維根數變化的信息。模塊“TAB 1”和“TAB 2”用于統計快慢速纖維的根數(N1和N2)；“TAB 3”和模塊“TAB 4”用于統計前后纖維的根數(M1和M2)；模塊“TAB 5”用于統計浮游纖維的根數(Mf)，而模塊“TAB 6”統計其中快速浮游纖維根數(Mff)的變化情況。Mf和Mff兩者的差值就是慢速浮游纖維的根數(Msf)。該建模方式的可行性已經在文獻[18]中進行了驗證，此處不再贅述。

2 條干不勻產生機理分析

2.1 仿真條件

文獻[18]中的仿真條件如表1和2所示。

表1 試驗用材料規格

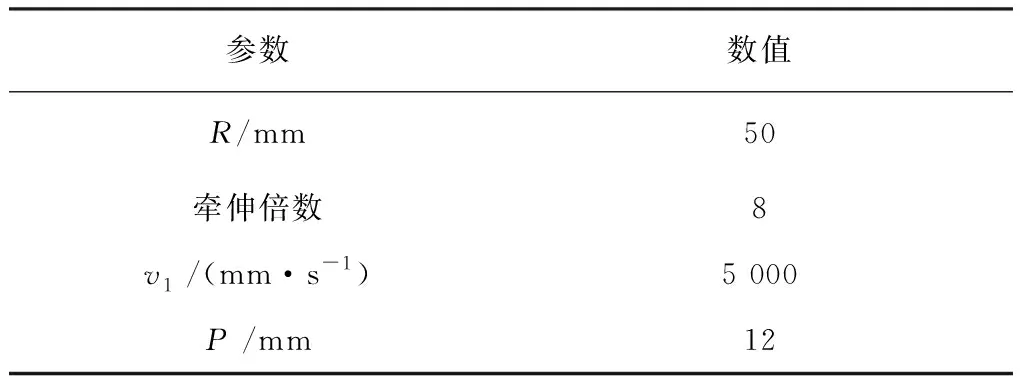
表2 牽伸工藝參數

采用3種理論分布來模擬研究纖維頭端分布形式對輸出條干不勻的影響效果: (1)均勻分布 (UNIFORM)；(2)指數分布 (EXPONENTIAL)；(3)伽馬分布 (GAMMA)。3種分布函數的均值相同，均表示模型中相鄰兩個活動實體產生的間隔時間T(1.2節中“GENERATE 1”的參數值大小)。其中，均勻分布的方差為T2/12，指數分布的方差為T2，伽馬分布的方差為T2/4。另外，為了同時研究纖維頭端間隔時間大小對輸出條干不勻的影響，將產生活動實體的時間間隔從T變成10T。文獻[18]中仿真纖維頭端間隔及其分布形式對輸出條干不勻的影響，如圖4所示，其中，Martindale的曲線為采用極限不勻的理論計算值。

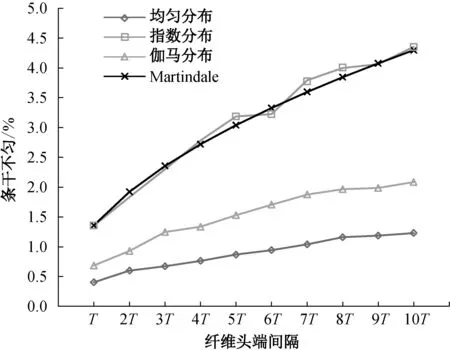
圖4 纖維頭端間隔及其分布對輸出條干不勻的影響Fig.4 Effect of the interval and distribution of fiber end on the output unevenness

2.2 仿真結果分析

纖維的頭端距離是指須條內相鄰的前后兩根纖維間相距的長度，其主要反映了纖維在須條中的排列情況。理論上，因為移距偏差現象的存在，在經過牽伸過程后，兩根纖維間的頭端距離會變大。由于本文在離散系統中建立的仿真模型是以時間為主導的，所以模型中相鄰兩根纖維間距離的大小是通過它們到達同一截面處相差的時間長短來判斷的。因此模型中，纖維頭端間隔的定義為兩根纖維到達同一截面的時間間隔大小，其均值為相鄰兩個活動實體產生的平均時間間隔T。

在同等仿真條件下，當須條內纖維頭端間隔為T且分別符合指數分布、均勻分布和伽馬分布時，牽伸區內快慢速纖維的分布情況如圖5所示。從圖5可以看出，須條內纖維頭端間隔的分布形式對牽伸區內快慢速纖維的分布情況無顯著性影響。

圖5 纖維頭端分布對快慢速纖維分布的影響Fig.5 Effect of fiber end distribution on the fast and slow fiber distributions

采用3種理論的頭端分布時，前后鉗口處的纖維根數隨纖維頭端間隔時長變化的情況如圖6所示。從圖6中可知，隨著纖維頭端間隔的增大，前后鉗口處的纖維根數均明顯減少，則仿真輸出條干不勻逐漸增大。另外，在相同的纖維頭端間隔下，輸入須條內的纖維頭端分布形式不同，并不會對輸入和輸出牽伸區的纖維根數造成明顯差異。但根據文獻[18]可知，不同的纖維頭端分布形式確實會對輸出條干不勻產生影響，這就說明模型的輸出條干不勻并不是因為須條截面內纖維根數的波動造成的，而是由于須條內纖維的排布不均而產生的。

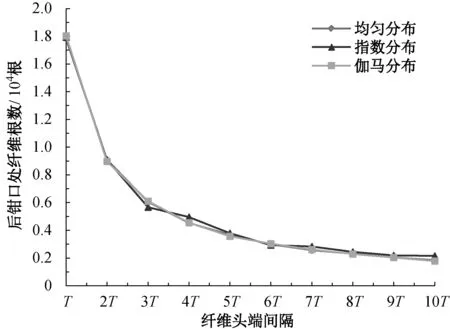
(a)輸入后纖維根數

(b)輸出前纖維根數圖6 纖維頭端間隔對前后鉗口處纖維根數的影響Fig.6 Effect of fiber end interval on the fiber number at the front and back nip line

當纖維頭端間隔為T時，不同纖維頭端分布形式下，牽伸區內慢速浮游纖維的分布情況如圖7所示。從圖7中可知，慢速浮游纖維的分布在前后鉗口附近處基本相同，其數量多少主要取決于牽伸區中部峰值處慢速浮游纖維的根數。因此，統計慢速浮游纖維分布的峰值隨須條內纖維頭端間隔的變化情況如圖8所示。

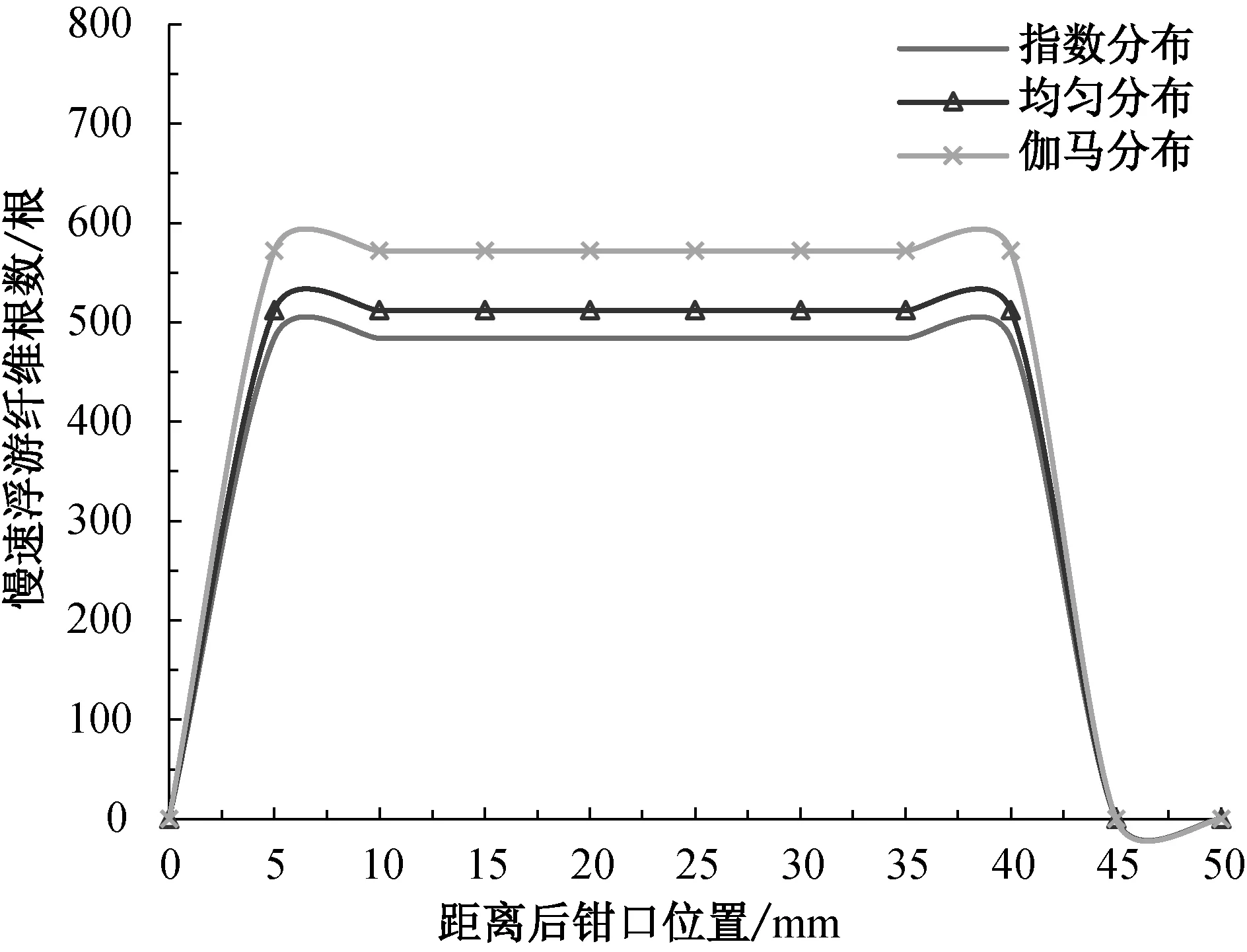
圖7 纖維頭端分布對慢速浮游纖維分布的影響Fig.7 Effect of fiber end distribution on the slow-floating fiber distribution

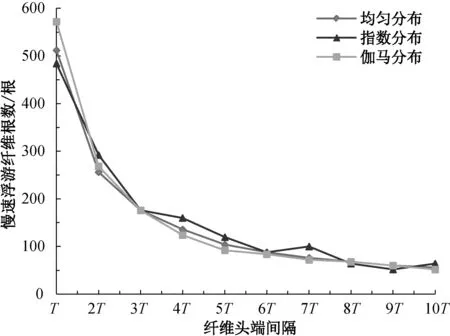
圖8 纖維頭端間隔對慢速浮游纖維根數的影響Fig.8 Effect of fiber end interval on the slow-floating fiber number

從圖8中可以看出，在3種纖維頭端分布形式下，慢速浮游纖維的根數均隨著頭端間隔時間的增大而減小，其中，當纖維頭端分布符合指數分布形式時，慢速浮游纖維根數的波動最大。相應地，牽伸區內快速浮游纖維根數的變化情況如圖9所示，快速浮游纖維占浮游纖維總根數的比值變化如圖10所示。

圖9表明，纖維頭端分布形式為指數分布時，牽伸區內的快速浮游纖維根數的波動最大。從快速浮游纖維的占比變化情況中，也可以說明這個問題(圖10(a))。為了更加詳細地說明每種纖維頭端分布形式對快速浮游纖維的影響，將快速浮游纖維隨纖維頭端間隔變化的波動比繪制于圖10(b)中。

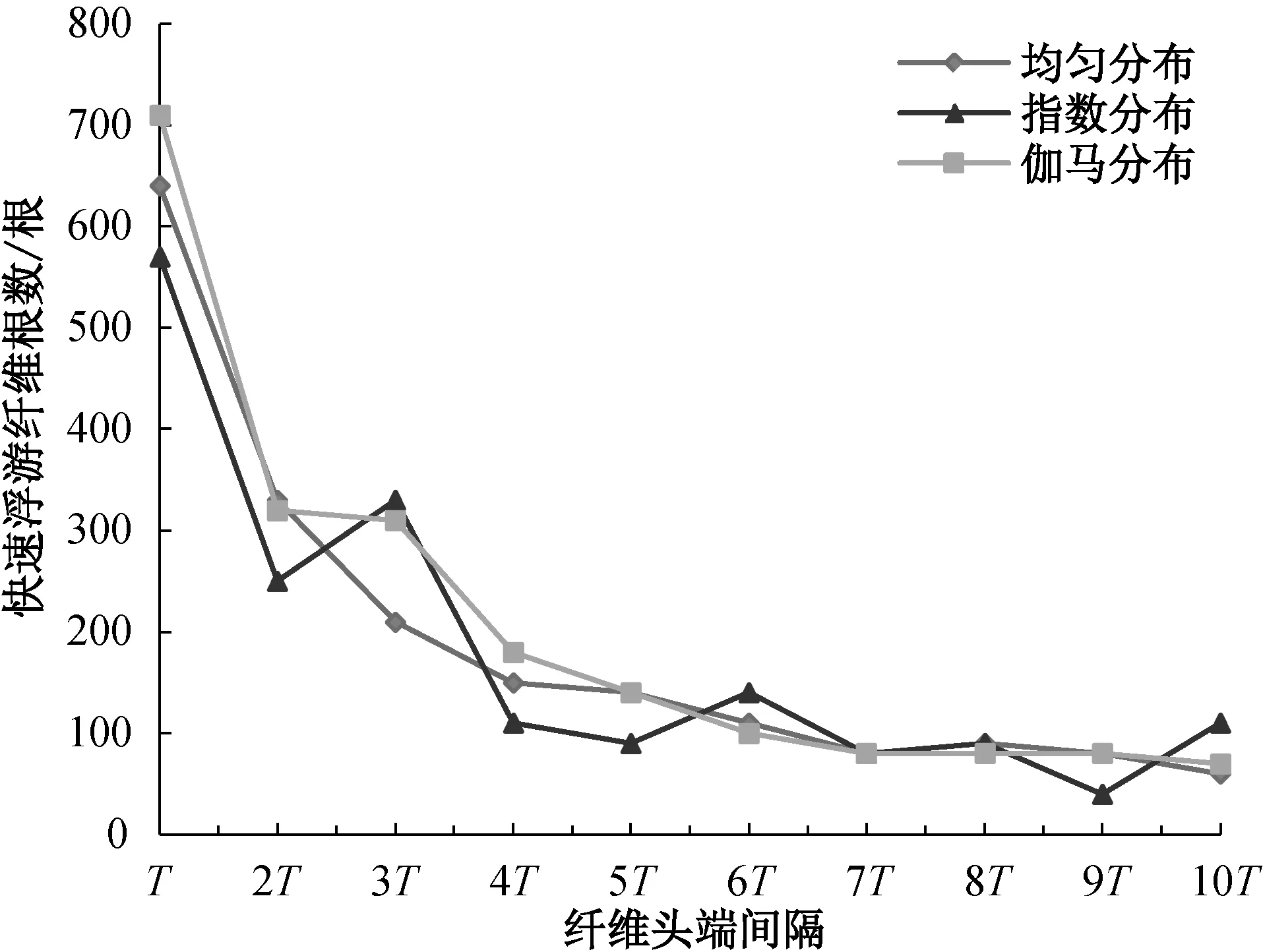
圖9 纖維頭端間隔對快速浮游纖維根數的影響Fig.9 Effect of fiber end interval on the fast-floating fiber number

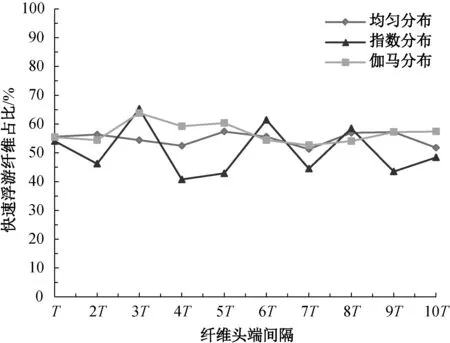
(a)快速浮游纖維占比

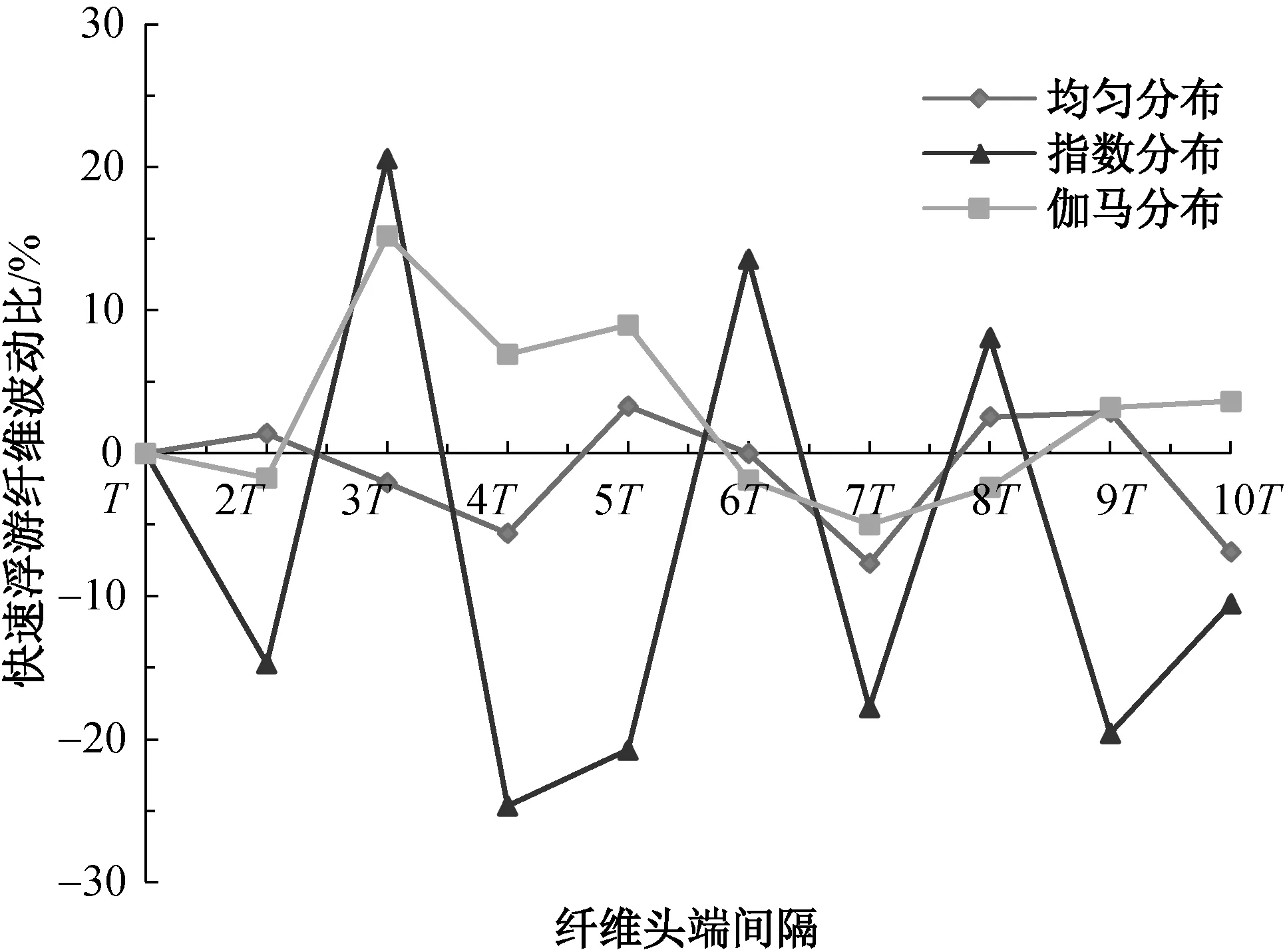
(b)快速浮游纖維波動比圖10 纖維頭端間隔對快速浮游纖維占比和波動比的影響Fig.10 Effect of fiber end interval on the proportion and fluctuation ratio of fast-floating fiber number

如果須條內纖維頭端間隔為T，牽伸區內快速浮游纖維的根數用N1T表示，則可以用NiT表示在纖維頭端間隔為iT時的快速浮游纖維根數，其中i為從1到10的整數。因此，可得出快速浮游纖維隨纖維頭端間隔的波動比為

(6)

由圖10(b)可知，纖維頭端分布形式符合指數分布時，牽伸區內快速浮游纖維對纖維頭端間隔的變化最為敏感，波動幅度最大，故牽伸后輸出條干不勻最大。相反，纖維頭端為均勻分布下快速浮游纖維的波動最小，則輸出條干不勻也小。

3 結 語

本文利用離散理論建立了一個紡紗牽伸改進模型，用于分析牽伸區內纖維的分布情況，闡述輸出條干不勻的產生機理。根據文獻[18]中給出的指數分布、均勻分布和伽馬分布的纖維頭端分布，模擬牽伸后輸出條干不勻的變化情況。本文在牽伸改進模型中，著重分析了纖維頭端間隔及其分布形式對牽伸區內各類纖維分布情況的影響，并闡述了條干不勻的產生機理，可得出如下結論:

(1) 纖維頭端間隔及其分布形式對須條的牽伸過程有顯著性影響；

(2) 牽伸區內各類纖維分布的波動才是產生輸出條干不勻的根源；

(3) 保持牽伸區內浮游纖維尤其是快速浮游纖維的根數及占比穩定，能夠有效地降低輸出須條的條干不勻。

這些研究結果為討論牽伸過程中的自調勻整問題提供了理論依據。