考慮風屏障效應的車橋系統三分力系數風洞試驗研究

王玉晶， 郭薇薇，2， 夏 禾，2， 張 楠，2， 張 田

(1. 北京交通大學 土木建筑工程學院，北京 100044； 2. 北京市結構風工程和城市風環境重點實驗室，北京 100044； 3. 大連海事大學 交通運輸工程學院，遼寧 大連 116026)

隨著高速鐵路的迅速發展，列車在強側風作用下的傾覆事故時有發生，風荷載作用下的行車安全問題變得愈加突出[1]。提高強風作用下列車安全性的措施主要有：優化車輛外形、通過強風監測系統控制列車運行速度和設置風屏障[2]。但是列車的降速或者停運會影響運營效率，造成一定的經濟損失。而風屏障可以為列車提供一個較低風速的風環境，進而有效提高列車行車安全性。因此，對于已有車輛來說，設置風屏障更加行之有效。

近年來，很多學者通過現場實驗、數值模擬與風洞試驗等方法對風屏障的防風性能進行了研究。結果表明[3-5]：在路基上設置風屏障可以大大提高列車的運行安全性，但對于橋梁來說，風屏障在減小列車運行區域風速的同時增大了橋梁的迎風面積，使橋梁的風荷載加大，這是不利的。因此，人們采用孔隙式風屏障來降低橋梁風荷載。郭文華、李永樂、何旭輝等[6-9]采用風洞試驗和數值模擬的方法研究了雷諾數、風攻角、風屏障參數(高度和透風率)對車橋系統氣動特性的影響，并給出了風屏障高度和透風率的建議取值。

列車的氣動力不僅受風屏障高度和透風率的影響，還與線路結構形式、風屏障的安裝位置和行車位置有關。本文采用風洞實驗的方法，對高速鐵路32 m簡支箱梁和16 m T梁的截面三分力系數進行了測試，對比分析了列車在不同梁型上的氣動特性，并與其在平地路基上的結果進行了對比；分析了風屏障安裝位置和行車位置對車橋系統氣動力系數的影響；選取一種工況進行了數值模擬，并與實驗結果進行對比，解釋了風屏障-車-橋系統氣動繞流機理；最后，對不同線路結構形式和風屏障安裝位置時車輛的行車安全性進行分析。

1 試驗概況

試驗在北京交通大學風洞實驗室進行。該風洞是一座雙試驗段回流大型多功能邊界層風洞，風洞試驗段尺寸為：3.0 m×2.0 m×15.0 m(寬×高×長)。試驗風速為8～10 m/s，風場湍流度小于0.5%。

1.1 試驗模型與測點布置

制作了風屏障-列車-箱梁、風屏障-列車-T梁和風屏障-列車-路基三種風洞試驗模型，如圖1所示。綜合考慮列車和橋梁的幾何尺寸、風洞高速段截面尺寸和阻塞度要求，模型(含風屏障、橋梁、列車等)的幾何縮尺比為1∶32，最大阻塞比為10.5%。

圖1 試驗模型Fig.1 Test models

列車模型是CRH2型高速列車的中間車，忽略了轉向架、輪對和門把手等細部結構，外形上與實物保持一致，以盡可能真實的模擬實際氣流的繞流。箱梁模型和T梁模型的長度為2.6 m，車輛模型長度為2.4 m。箱梁和車輛模型均以鋼管為骨架，外殼采用ABS板制作，以保證模型具有足夠的剛度和強度，在試驗中不變形且不出現明顯的振動以保證測試的精度。T梁模型采用薄鋼板直接沖壓而成，用木質板模擬路基。風屏障模型是長度為2.6 m的圓孔式ABS板，通過三角支撐固定在線路結構表面，保證其在試驗過程中不發生變形。箱梁模型和T梁模型距地面1.0 m，路基模型距地面0.5 m，車橋間距為0.02 m。

圖2 測點位置及編號Fig.2 Pressure taps on vehicle surface

本試驗采用壓力積分法計算作用在車輛上的氣動力，因此在沿列車長度方向在車體表面布置5個測壓斷面。為排除洞壁的氣動干擾效應，將其中2個測壓斷面布置在車輛兩端。如圖2(a)所示，在列車中間對車布置3個測壓面，數據分析時取中間3個截面計算結果的平均值。圖2(b)所示為每個測壓面的測點布置，考慮測量結果的準確性、車輛橫截面尺寸和車輛模型內的走線情況，每個測壓面上布置40個風壓測點，共200個風壓測點。

1.2 測試儀器

試驗分為兩部分：橋梁剛性模型的靜力實驗和車輛模型的測壓實驗。

靜力實驗是通過連接于橋梁模型兩端的桿式五分量測力天平測得系統整體的氣動力。測力天平可以測得橫橋向、豎橋向兩個方向的力及橫橋向、豎橋向和縱橋向三個方向的力矩分量。梁體通過測力天平與轉盤相連，并通過電機驅動轉盤來精確控制來流與試驗模型的夾角，即風攻角α。

測壓試驗的測試對象是車輛，在測試時通過螺栓將車輛固定在橋梁或路基的表面，采用美國PSI公司的電子壓力掃描閥測試車輛表面的風壓。壓力采集設備為美國PSI公司生產的4個ESP-64HD微型壓力掃描模塊，可實現256個點的高速同步測壓。采樣時長是80 s，采樣頻率為312.5 Hz。

試驗中，車輛和橋梁相接觸。通過測壓試驗得到車輛的三分力，通過測力試驗得到車橋系統整體的三分力，最后通過力的合成定理計算得到作用在橋梁上的三分力。

1.3 實驗工況

選用CRH2型高速列車和大風區常用的箱梁、T梁和路基作為研究對象，測試風屏障對提高列車安全性能的影響。參考文獻[10]，選取高度為3.5 m、透風率為30%的圓孔式風屏障，分析不同工況下車輛和橋梁的氣動力，表1所列為試驗的工況安排，按照不同的線路架構形式、風屏障位置、立車行車位置、風攻角、風速等，共設計了318個吹風工況。

表1 試驗工況Tab.1 Test cases

2 試驗結果與分析

2.1 三分力系數

不同風攻角下作用在模型上的氣動力可用三分力描述，即側力FD(α)、升力FL(α)和力矩M(α)，M(α)作用在模型的幾何形心,三分力系數計算如式所示

(1)

式中：CD(α)、CL(α)、CM(α)分別是風軸坐標系下的側力系數、升力系數和力矩系數；α為來流攻角(°)；U為來流風速(m/s)；ρ為空氣密度(ρ=1.225 kg/m3)；H、B和L分別為節段模型的高度、寬度和長度(m)。

2.2 線路結構形式的影響

箱梁、T梁和路基的存在會不同程度地影響列車周圍的風場，因此將箱梁、T梁和路基三種不同線路結構形式下車輛的氣動力進行對比。

表2所示為風攻角α=0°時，不同線路結構形式下的車輛三分力系數測試結果。可以看出：①風速分別為8 m/s、9 m/s和10 m/s時，相同線路結構形式上車輛的三分力系數都比較接近。即當風速在一定范圍內變化時，其對車輛氣動力特性的影響較小，可以忽略。因此，可取不同風速下車輛三分力系數的均值進行分析。②車輛在不同線路結構上的力矩系數都很小，對車輛影響可以忽略，車輛安全性主要由側力系數和升力系數控制。對比側力系數和升力系數可知，當車輛在路基上運行時最安全。而車輛在不同線路結構形式上的力矩系數都很小，接近零。

表2 車輛三分力系數Tab.2 Tri-component coefficients of vehicle

圖3給出了箱梁和T梁上車輛三分力系數隨風攻角的變化規律。從側力系數上看，列車在箱梁和T梁上時側力系數隨風攻角先減小后增大。但車輛在箱梁上時，CD的最小值出現在α=-2°，而在T梁上時，CD在α=+2°時最小。升力系數CL隨風攻角的增加而線性減小，在-2°附近相等。但是由于箱梁和T梁的截面形狀不同，當風攻角大于-2°時，箱梁上車輛的CL減小更迅速。與升力系數相反，力矩系數隨風攻角的增加而增加，且在-2°附近時兩者最為接近。箱梁的力矩系數增加了161%，T梁的增加了77.6%。

圖3 車輛在不同梁型上的三分力系數Fig.3 Tri-component coefficients of vehicle at different bridges

2.3 風屏障位置的影響

選取箱梁這一典型的結構形式，分析車輛位于迎風側和背風側時，風屏障安裝位置(在迎風側安裝單側風屏障和安裝雙側風屏障)對車橋系統氣動特性的影響。

圖4(a)給出了不同風攻角下箱梁上安裝單側風屏障和雙側風屏障時迎風側車輛三分力系數的變化規律。對比可知，風屏障安裝位置不同時，車輛的氣動力系數都很接近。只有風攻角在-2°～+4°范圍內且安裝雙側風屏障時的CL略小于安裝單側風屏障時的CL。這是由于當來流經過迎風側的風屏障時，只有部分氣流穿過，其余氣流在風屏障頂部和橋梁底部發生繞流，而作用在車輛表面的氣流在車頂和車體迎風面的交界處又發生二次繞流，因此經過迎風側風屏障和列車的雙重阻擋作用后，位于背風列車區域的風場已經較弱。在背風側安裝孔隙式風屏障對此區域流場的影響較小。因此，安裝雙側風屏障對車輛氣動力影響很小。

圖4(b)給出了不同風攻角下背風側車輛三分力系數的變化規律。對比可知，安裝雙側風屏障后背風側列車的CD都大于安裝單側風屏障時的值，而CL在-6°～+2°范圍內也都大于單側風屏障的情況，風攻角為+4°和+6°時，安裝單側風屏障時較大，分別比安裝雙側擋風屏時大37.4%和23.1%。在任何風攻角下，兩者的CM很接近，安裝背風側風屏障對力矩系數的影響可以忽略。這是由于背風側風屏障的存在使得列車下游的風場減弱，而對迎風側風屏障和列車之間的風場影響很小。

圖5(a)給出了在不同位置安裝風屏障且車輛位于迎風側時橋梁三分力系數隨風攻角的變化規律。可以看出，橋梁的側力系數隨風攻角的增加持續增加，且安裝雙側風屏障時的CD一直大于安裝單側風屏障時的CD。α在-2°～+6°時，雙側風屏障時橋梁的升力系數小于單側風屏障時的升力系數。力矩系數基本相等，且數值隨風攻角變化較小，但風攻角從-6°到+6°時，單側風屏障和雙側風屏障時橋梁的CM增幅都很大，分別為96.7%和159%。背風側風屏障的存在增大了橋梁的迎風面積，但由于迎風側風屏障和車輛對側風的雙重阻擋作用，作用在背風側風屏障上的力明顯減小。

圖4 車輛三分力系數Fig.4 Tri-component coefficients of vehicle

圖5(b)給出了車輛位于背風側時橋梁三分力系數隨風攻角的變化規律。可知，α在-2°～+6°時，橋梁的三分力系數均比較接近。而在-6°～-4°時，安裝雙側風屏障的CD和CM偏大，而CL偏小。由于背風側風屏障距離背風側列車較近，因此列車位于背風側時，背風側風屏障的存在對風場的影響較小，只是在某些風攻角下對橋梁的氣動特性有所影響。

圖5 橋梁的三分力系數Fig.5 Tri-component coefficients of bridge

2.4 行車位置的影響

雙線鐵路一般會存在雙車的情況，迎風側車、背風側車和橋梁之間存在不可忽略的氣動干擾效應。以安裝單側風屏障的箱梁為分析對象，單車(包括迎風側車和背風側車)和雙車時車橋系統的氣動力系數如表3所示。

表3 不同行車位置時的車橋三分力系數Tab.3 Tri-component coefficients of train-bridge system α=0°

從表3中可以看出，單車時，迎風側車的氣動力系數都大于背風側車，而橋梁的氣動力系數都略微偏小。雙車存在時，迎風側車的氣動力系數仍然大于背風側車，橋梁的氣動力系數基本不變。背風車的存在使得迎風側車的CD減小了5.3%，但CL增加了21.1%。迎風車的存在使得背風側車的CD和CL分別減小了244.4%和33.3%，而CM增加了33.3%。

圖6(a)所示為單車和雙車時迎風側車的三分力系數隨風攻角的變化規律。可見，有無背風側列車時，車輛的氣動力系數隨風攻角的變化趨勢一樣，數值也基本相同。這是由于迎風側車的下游區域風速較小，背風側車對迎風側車的氣動干擾較小，亦即背風側車的存在對迎風側車的氣動特性影響較小。

圖6(b)所示為單車和雙車時背風側車的三分力系數隨風攻角的變化規律。可看出，迎風側車對背風側車的三分力系數影響較大，尤其明顯的是側力系數。雙車存在時，背風側車的側力系數明顯減小，甚至有負數的情況，這是由于迎風側車的遮風效應減小了背風側車上的風荷載，以至受到“吸引”作用。在所有風攻角情況下，背風側車的升力系數也小于雙車時。

圖6 車輛三分力系數Fig.6 Tri-component coefficients of vehicle

圖7所示為單車(迎風側車和背風側車)運行和雙車3種工況下的橋梁三分力系數。可以看出，隨著風攻角的增大，橋梁的側力系數和力矩系數也都隨之增大，相反升力系數隨之減小。當風攻角大于-2°時，背風側行車的橋梁CD和CM最大，而迎風側行車時最小；在-6°～-2°時，三種行車工況下橋梁的CD和CM較為接近。三者的CL在+3°附近相等，當風攻角大于+4°時，迎風側行車時橋梁的升力系數又成為最大值。這是由于風攻角改變后，迎風側車和背風側車與橋梁之間的流場發生改變，氣動干擾效應也發生相應變化。

圖7 橋梁的三分力系數Fig.7 Tri-component coefficients of bridge

3 CFD數值模擬

對風洞縮尺模型的測試精度進行對比驗證，選取安有單側風屏障的車-橋系統進行CFD數值模擬，車輛分別位于迎風側和背風側。建立三維數值模型，數值模型的尺寸與風洞試驗中模型的尺寸相同，計算域的尺寸為8.4 m×4.4 m×0.4 m，網格采用六面體網格形式，數量為1 042萬。采用RNGk-ε湍流模型，設定來流面為速度入口邊界條件，出口為靜壓為零的壓力出口邊界條件，上表面為滑移壁面，地面為無滑移壁面，風速取為10 m/s，計算結果列于表4中。

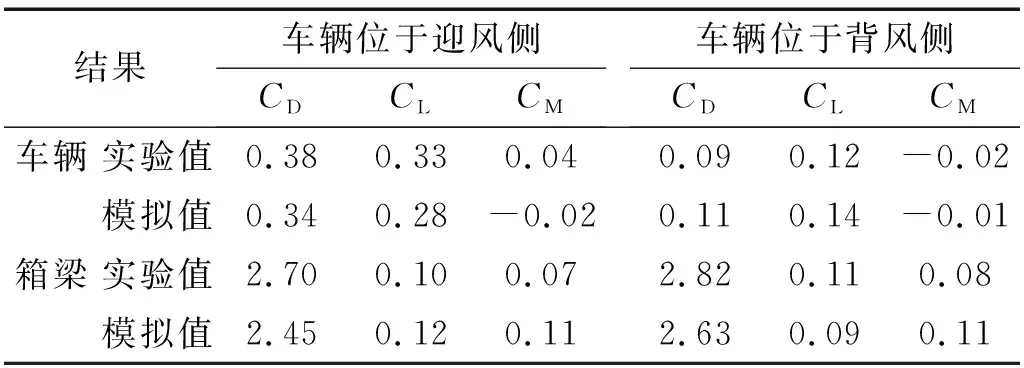
表4 風洞試驗與數值模擬結果對比Tab.4 Comparisons ofresults from tests and simulation

從表4知，數值模擬與試驗得到的CD和CL較為接近，擋風屏后風場復雜且CM本身較小，因此差別稍大。

圖8所示為車橋系統的壓強分布云圖。從圖中可知風屏障的存在改變了車橋系統周圍的流場，側風直接作用在風屏障上，風屏障無孔處的壓強最大值為70 Pa左右，而在開孔位置氣流流速加快，使得列車迎風面的壓強成為負值。風屏障和列車迎風面之間的渦流變化復雜，壓強最小值出現在列車迎風面和上表面交界處，約為-140 Pa。且在車橋系統的下游出現了較大漩渦，漩渦不斷地脫落。

圖8 壓強分布云圖(Pa)Fig.8 Contour of pressure distribution (Pa)

4 列車安全性分析

高速列車在強側風下發生傾覆，主要是高速列車的側力、升力和二者共同產生的側傾力矩過大造成的，其中側傾力矩是衡量列車橫風穩定性最重要的指標，為便于分析，轉換成側傾力矩系數[11]。如圖9所示，將實驗得到的作用于列車幾何形心的三分力轉換到作用于左右輪軌接觸軸線上的力矩Ml和Mr，再進行無量綱化，即可得到CMl和CMr。

圖9 側傾力矩系數Fig.9 Rolling moment coefficient

左右軌線上側傾力矩系數的計算如式(2)所示

(2)

式中：CD、CL、CM分別為相對于車輛形心的側力系數、升力系數和力矩系數；b為車輛形心至軌道的水平距離(m)；h為車輛形心至軌道的垂直距離(m)。

在不同線路結構形式和風屏障位置下，左右軌線上的側傾力矩系數，如表5所示。

由表5可知，右軌線上的側傾力矩系數總是大于左軌上的側傾力矩系數。在不同線路上時，列車的CMl基本相同，而在箱梁上時CMr最大，而在路基上的側傾力矩系數最小。相對于單側風屏障的情況，安裝雙側風屏障并沒有有效改善列車的抗側傾能力，相反卻使列車相對于右軌線的側傾力矩系數略微增大。

表5 車輛的側傾力矩系數Tab.5 Rolling moment coefficients of vehicle

5 結 論

針對高速列車在箱梁、T梁和路基三種不同結構形式上運行的系統模型進行節段模型風洞試驗。對實驗結果進行分析可以得出如下結論：

(1) 當風速在一定范圍內變化時，風速對車輛三分力系數的影響較小，可以忽略。較于箱梁和T梁，列車在路基上運行時的側力系數、升力系數和力矩系數均最小，行駛較安全。

(2) 安裝單側風屏障和雙側風屏障時，車輛的氣動力系數都很接近。只有風攻角在-2°～+4°范圍內且安裝雙側風屏障時CL略小于安裝單側風屏障時的CL。背風側風屏障的存在增大了橋梁的迎風面積，但是由于迎風側風屏障和車輛的遮風效應，作用在背風側風屏障上的氣動力明顯減小。

(3) 雙車存在時，迎風側車的下游區域風速較小，背風側車對迎風側車的氣動干擾較小，而迎風側車對背風側車的氣動特性影響較大。在不同行車工況下，橋梁的側力系數和力矩系數也都隨風攻角增大而增大，相反升力系數隨之減小。

(4) 數值模擬與實驗得到的CD和CL較為接近。風屏障的存改變了作用于迎風側車周圍的風場，并且在車橋系統下游產生較大漩渦。

(5) 車輛對右軌線的側傾力矩系數總是大于對左軌線的側傾力矩系數。在不同線路上時，車輛的CMl基本相同，而CMr在箱梁上時最大。安裝雙側風屏障并沒有明顯改善列車的抗側傾能力。