基于非對稱復合材料層合板的準零剛度隔振系統
郭懷攀, 李 昊, 陳衛東, 周徐斌
(1. 南京航空航天大學 機械結構力學及控制國家重點實驗室, 南京 210016;2. 上海衛星工程研究所, 上海 200240)
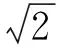
雙穩定層板是一種具有兩種穩定構型的非對稱鋪設復合材料層板結構[9-11],因其在構型轉變過程中顯示出非線性及負剛度特性,有學者開始研究用其作為負剛度機構,構建準零剛度隔振系統,Shaw等[12]發現使用雙穩定層板可以減小隔振結構的固有頻率而不降低結構的承載能力。陸澤琦[13]系統的研究了雙穩定層板的負剛度特性,并將其引入雙層隔振系統進行試驗研究,發現結構中加入雙穩定層板后能改善系統的隔振性能。
本文利用理論和有限元方法研究了正交鋪設復合材料層板的非線性特性。通過分析及設計,使得正交非對稱層板具有準零剛度特性。采用準零剛度正交非對稱層板作為隔振器進行隔振研究,預測其隔振效率,并與線性隔振系統進行比較。探究將其運用于衛星微振動控制的可行性。
1 理論模型
雙穩定層板為非對稱鋪層,層板在制造溫度時板為平板構型,由于預浸料在垂直纖維方向的熱膨脹系數與沿纖維方向熱膨脹系數的不同,在層板冷卻至室溫過程中,垂直纖維方向與沿纖維方向均產生殘余熱應力,層板在殘余熱應力作用下產生固化變形。圖1所示為正交鋪設層板中殘余熱應力在垂直纖維方向與沿纖維方向的單位長度的截面內的合力與合彎矩。
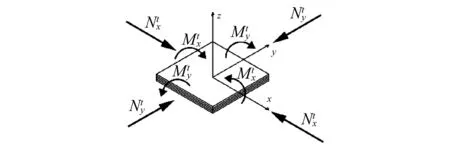
圖1 正交層板中殘余熱應力的合力與合彎矩示意圖Fig.1 Sketch map of resultant force and resultant moment of residual thermal stress in cross-ply laminates
假設層板中心固定限制其平動及轉動。利用Hamilton法則Lagrangian方程的一階變分在時間上的積分為零建立層合板動力學模型。
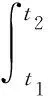
(1)
式中:T為板的動能;∏為板的總勢能;WF為外力對板做的功。
1.1 層合板總勢能
正交鋪設雙穩定層板的坐標系如圖2所示,坐標系的原點為層板中心點,坐標主軸與層板邊緣平行。層板鋪設以中心面(即坐標軸xoy面)為分界中心面以下為0°鋪層,以上為90°鋪層,0°鋪層與90°鋪層厚度相等,文中所描述層合板厚度均為層合板總厚度。

(a)非穩定構型 (b)穩定構型1 (c)穩定構型2圖2 正交鋪設雙穩定層板坐標示意圖Fig.2 Cartesian coordinate system for cross-ply bistable laminate
根據Kirchhoff假設,可得到雙穩定層板面內應變表達式為
(2)
(3)
因為雙穩定層板的大變形,在計算其中心面應變時需引入von Karman幾何非線性假設,得到雙穩定層板的中心面應變表達式為
(4)
考慮殘余熱應力影響,層板每一各向異性層(如第k層)的應力與應變關系在層合板坐標系下的表達式為
(5)
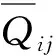
聯立式(2)、(4)并在層合板厚度方向上積分,可以得到層合板單位長度上的合力與合力矩。
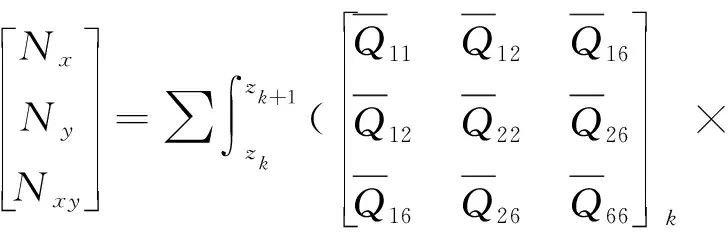
(6)
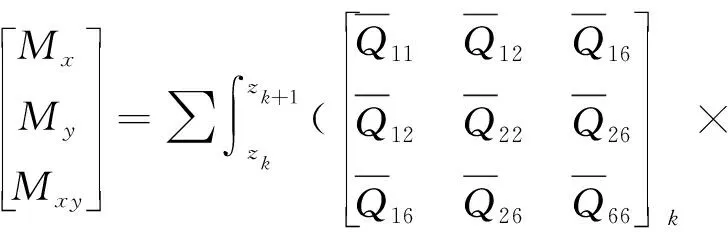
(7)
式(6)、(7)可以改寫為:
(8)
式中:A、B、D矩陣分別為層板的拉伸剛度矩陣、拉彎耦合剛度矩陣以及彎曲剛度矩陣:

(9)
Nt和Mt分別為層合板的殘余熱應力在層合板厚度方向上積分得到的合力和合彎矩:
(10)
最后,層合板的總勢能可寫為:
(11)
式中:Lx和Ly分別為層合板的平面尺寸。
因為層合板為非對稱鋪層,層合板內部存在拉彎耦合,因此,層合板中心面上的應變包含薄膜應變和彎曲應變。由式(9)可知,層合板的拉伸剛度矩陣與層合板厚度方向上坐標零點的位置無關,可得層合板在截面上的合力與薄膜應變的關系為:
N=Aεm
(12)
式中:εm為層合板的薄膜應變,聯立式(12)與式(8),可以得到層合板的薄膜應變與中心面應變之間的關系式為
ε0=εm-A-1BK+A-1Nt
(13)
對于正交鋪設層合板,其彎曲方向與坐標軸平行,結合邊界條件以及層合板變形的對稱性特點,可假設正交鋪設層合板的面外位移函數為:
w=ax2+by2+a1x4+b1y4+
a2x6+b2y6+ex2y2
(14)
式中:ai,bi,e為未知參數,則可求得層合板彎曲曲率為:
(15)
假設層合板的薄膜應變形式為:
(16)
式中:ci,di為未知參數。將式(16)代入式(13)可得到層合板的中心面應變,對層合板中心面應變積分可得到層合板中心面面內位移函數,聯立式(14)可求得層合板的中心面剪切應變。
1.2 外力做功
為了驅動雙穩定層合板從一種穩態跳變到另一種穩態,需要雙穩定對層合板施加驅動力,學者們研究了利用形態記憶合金[14],壓電智能材料[15]以及施加集中載荷[16]等方法驅動雙穩定層合板跳變。本文中在雙穩定層合板四個角點施加集中載荷驅動雙穩定層合板跳變。在這種驅動方式下外力做功為:
(17)
式中:f為每個角點作用的集中力。
1.3 層合板總動能
層合板中心固定,忽略面外轉動,可得到正交鋪設層合板總動能表達式為:
(18)
層合板的總動能的一階變分在時間上的積分為:
(19)
化簡式(19)可得,
(20)
1.4 構型預測
根據最小能量原理,可以預測雙穩定層合板在殘余熱應力以及驅動載荷作用下的靜態構型,雙穩定層合板靜態構型預測表達式為:
δWF-δ=0
(21)
聯立式(2)、式(17)代入式(21)可得到,
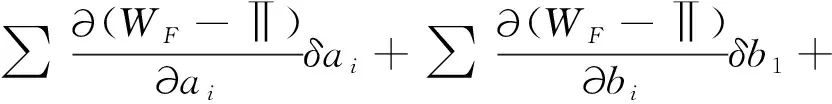
(22)
當式(22)中每一項都等于0時,將得到一組關于未知參數ai,bi,ci,di,e的非線性方程組(23):
(23)
因為fci,fdi為關于未知參數ci,di的線性方程,則ci,di可以用關于未知參數ai,bi,e的方程表示,則方程組(23)可簡化為7個非線性方程,得到方程組(24):
K(X)-F(X)=0
(24)
式中:
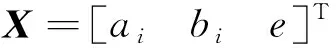
(25)
方程組(24)的解對應雙穩定層板的平衡構型,通常方程組(24)存在多組解,對于雙穩定層板的穩定構型,Jacobian矩陣(26)必須為正定矩陣:
(26)
1.5 動力學方程
將雙穩定層合板的總勢能、總動能以及外力做功代入方程(1)化簡,可得到雙穩定層合板運動的動力學方程。
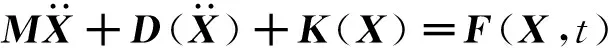
(27)
式中:M為雙穩定層合板的質量矩陣,可通過式(20)求得。F(X,t)表示式(17)中的角點集中力隨時間變化。在理論模型中為了考慮阻尼影響,假設了Rayleigh阻尼,由于本文主要研究層板在較低頻率下的振動響應,可假設層合板的剛度阻尼系數為0,則層合板的阻尼形式為:
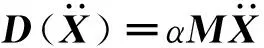
(28)
式中:α為層合板的質量阻尼系數。
2 靜力分析
層板所用材料體系為CCF300/5428,0°和90°鋪層厚度相同,材料參數見表格1。層板的固化溫度為140℃,假設室溫為20℃,則層板從固化溫度到室溫的溫度差為ΔT=-120℃。

表1 CCF300/5428材料參數Tab.1 Material properities of the CCF300/5428
2.1 構型預測
利用ABAQUS中殼單元建立100 mm×100 mm正方形正交鋪設的雙穩定層板的有限元模型,約束層板中心的位移和轉動。在第一個靜態分析步內將溫度場從層板固化溫度冷卻到室溫,結果顯示層合板構型為非穩定的馬鞍面構型。為了得到層合板的穩定構型,重啟靜態分析步在層合板四個角點施加沿z軸方向的微小集中載荷,第二靜態分析步結束后,再次進行靜力學分析去除在層合板角點施加的載荷,即可得到無外載荷作用下雙穩定層合板的穩定構型,改變載荷沿z軸的正負方向,可得到兩種不同的穩定構型。改變層合板的厚度,有限元分析及理論計算得到的無外載荷作用下層合板穩定狀態的角點面外位移與層合板厚度關系曲線如圖3所示。
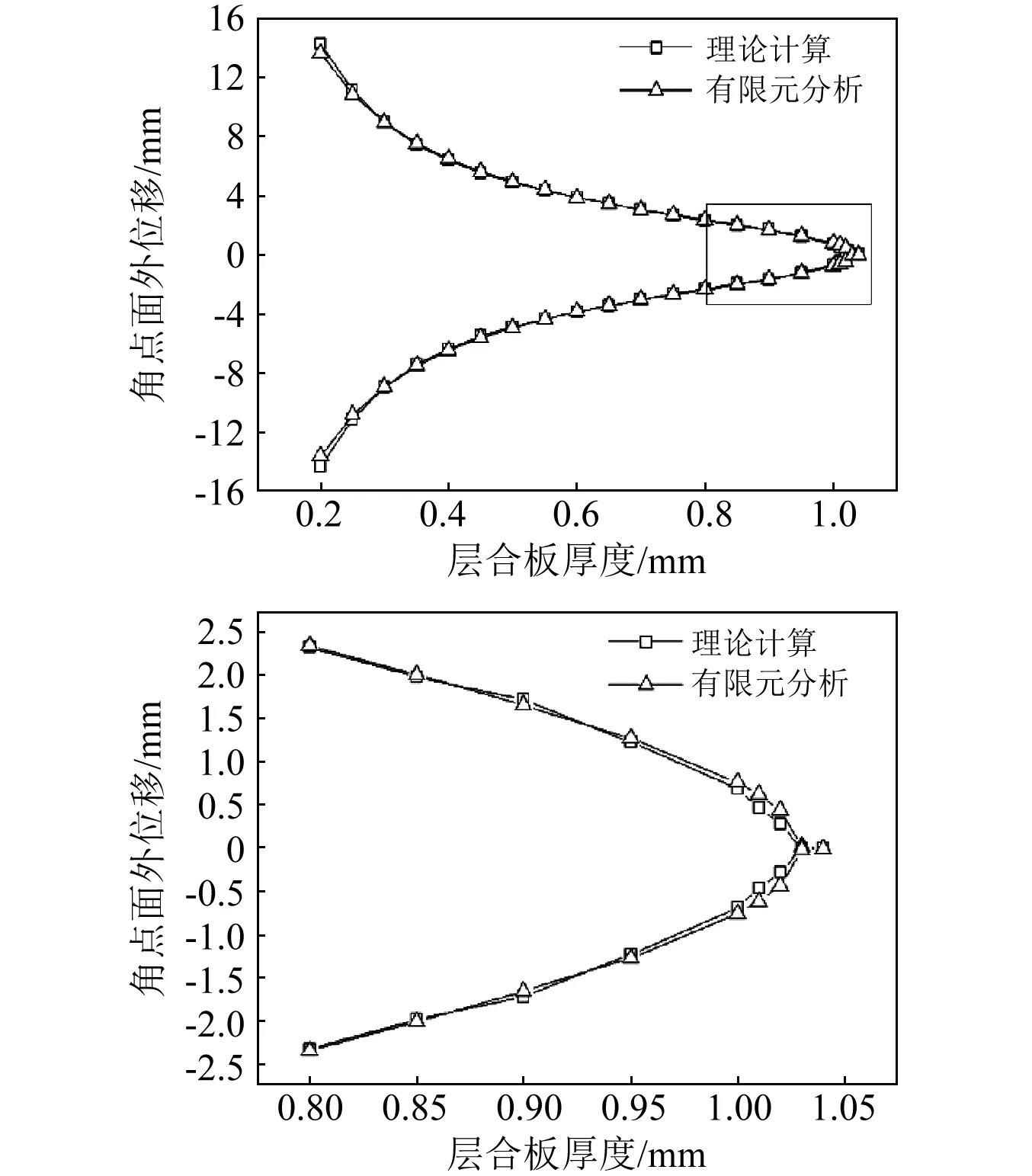
圖3 正交鋪設層板厚度參數分析Fig.3 Parametric analysis of laminate thickness for cross-ply laminate
圖3所示理論計算結果與有限元分析結果吻合的很好,當層合板厚度達到一定尺寸時會失去雙穩定特性,此時層合板的穩定構型為馬鞍面構型。有限元分析得到的層合板失去雙穩定性的臨界厚度約為1.028~1.032 mm,理論計算得到的臨界厚度約為1.022~1.026 mm。原因是理論模型中共有17個未知參數,即模型具有17個自由度,而在有限自由度的限制下理論模型無法精確表征層合板的局部變形;相比之下,有限元模型中由于節點數較多,其自由度遠大于理論模型。因此,理論模型與有限元模型所預測的雙穩態臨界厚度存在一定誤差。
為研究層正方形正交鋪設合板層合板幾何尺寸以及材料屬性對其失去雙穩定特性臨界厚度的影響,利用理論計算方法得到了不同材料層合板邊長與臨界厚度的關系,如圖4所示。預測結果顯示,當材料確定時,層合板失去雙穩定特性的臨界厚度與其邊長呈線性關系。
2.2 剛度分析
利用有限元分析,在層合板四個角點施加位移驅動,得到不同厚度情況下層合板角點力位移關系曲線如圖5所示,由圖5中(a)、(b)、(c)可以發現當層合板具有雙穩定性時,層合板在角點面外位移為0附近的一定位移區間內具有負剛度特性,并且隨著層合板厚度增加具有負剛度特性的位移區間逐漸變窄,當層合板厚度增加到1.032 mm時,層合板失去雙穩定構型。此時層合板無外載荷作用下的穩定構型為馬鞍面構型,角點力位移關系曲線如圖5(d)所示,在其平衡位置附近的位移區間內,層合板剛度趨近于零,隨著角點偏離平衡位置的位移增大,層合板剛度非線性增大,此種狀態層合板具有準零剛度特性。
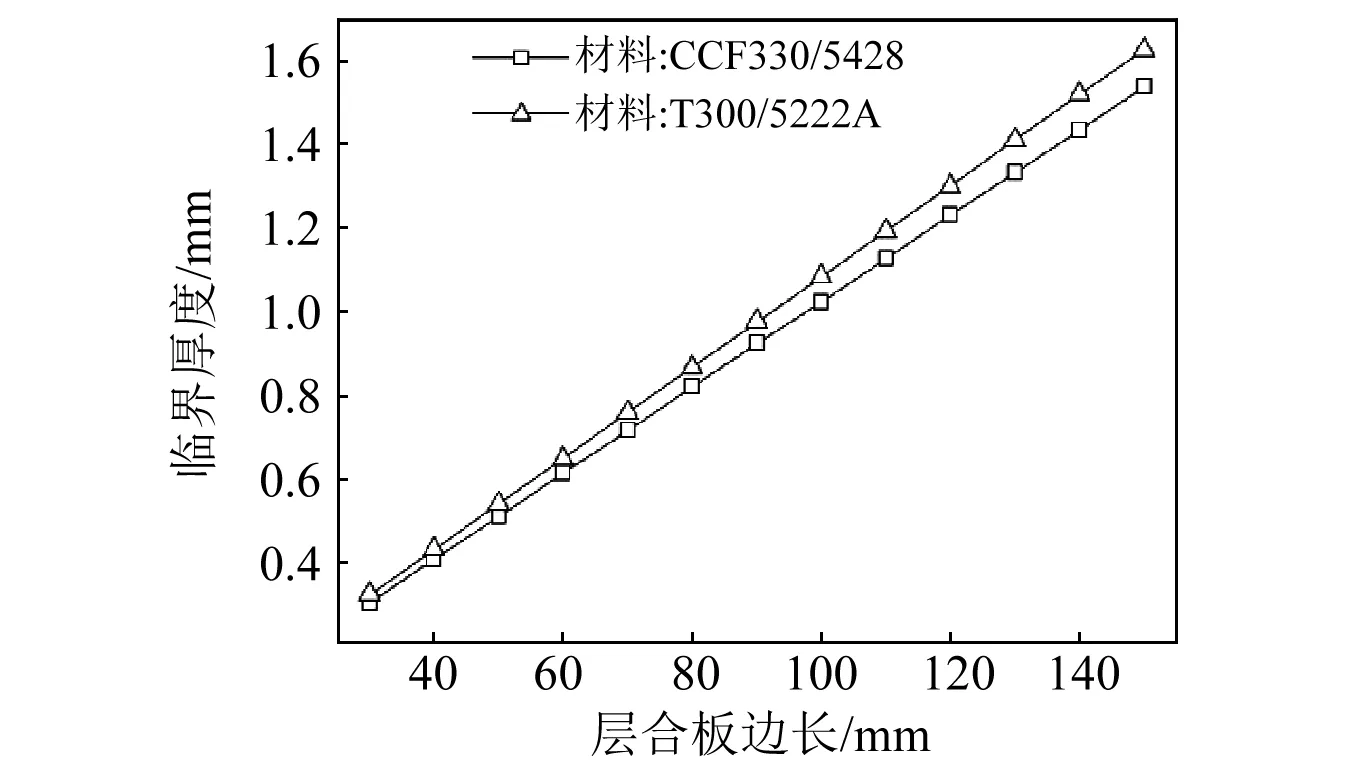
圖4 不同材料層合板長度與臨界厚度關系Fig.4 Length-critical thickness curve of different materials
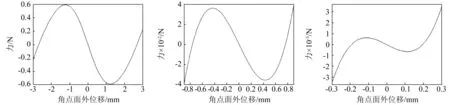
(a)層合板厚0.7 mm (b)層合板厚1 mm (c)層合板厚1.028 mm
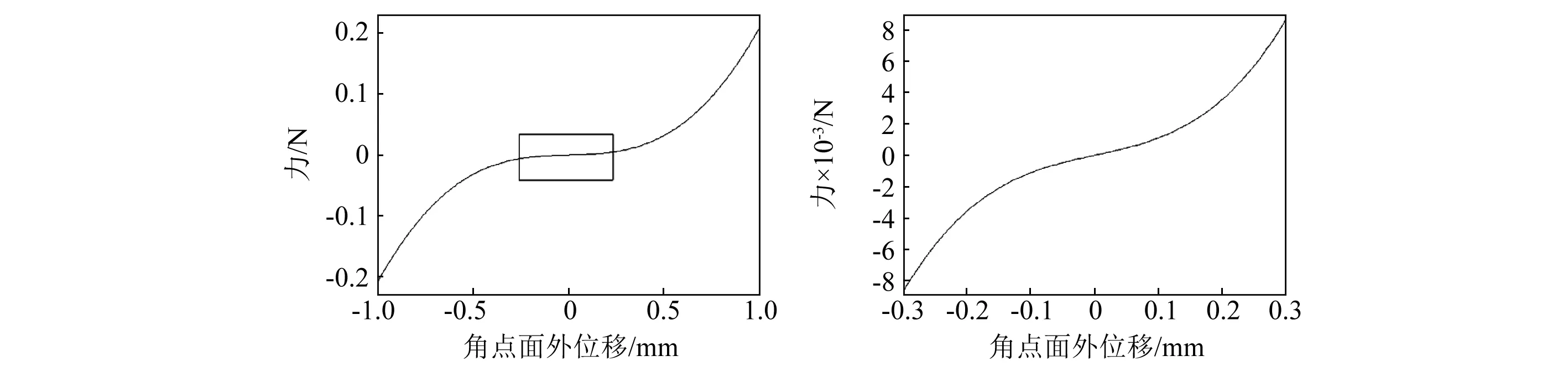
(d)層合板厚1.032 mm (e)層合板厚1.032 mm局部圖圖5 層合板角點力位移關系Fig.5 Corner node force-displacement curve
對比圖5(c)、圖5(d)有限元分析結果顯示在層合板臨界厚度附近,層合板厚度發生微小變化會引起其剛度發生顯著變化。理論模型計算顯示層合板的臨界厚度約為1.026 mm,表格2中對比了層合板在微小載荷作用下的角點面外位移,圖6中對比了層合板力位移關系曲線有限元分析結果與理論計算結果。結果顯示層合板厚為1.032 mm時,理論模型與有限元模型結果存在較大誤差。理論模型層合板厚度為1.026 mm時與有限元模型層合板厚度為1.032 mm時層合板剛度特性基本吻合。即理論模型中當層合板厚度為1.026 mm時具有準零剛度特性。
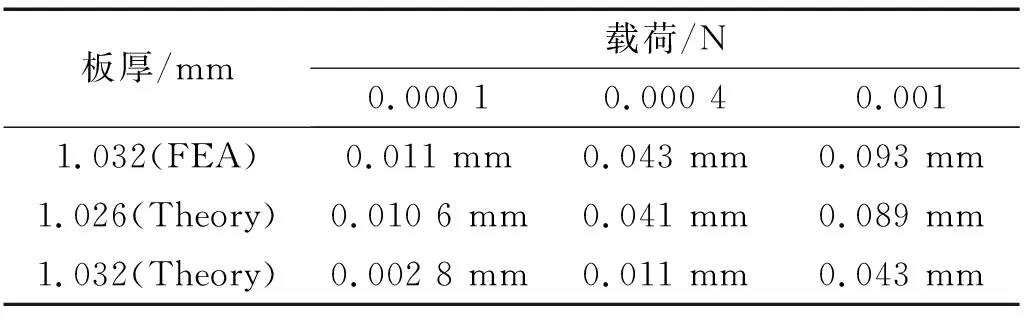
表2 不同載荷作用下角點面外位移對比Tab.2 Out-of-plane displacement of corner node with different load
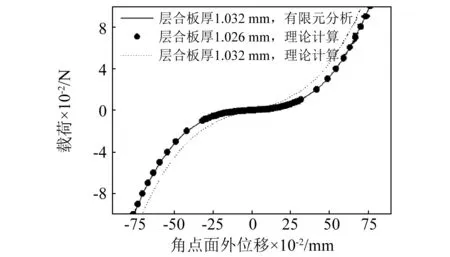
圖6 層合板角點力位移關系對比Fig.6 Contrast of corner node force-displacement curve
3 隔振研究
已有的利用雙穩定層合板進行振動控制的研究中,雙穩定層合板作為負剛度機構與其他正剛度機構組合構造準零剛度系統進行隔振[12-13],其中正剛度機構用于承載被隔振設備自重。有限元分析結果圖5顯示當層合板厚度為1.032 mm時,層合板具有準零剛度特性,此狀態下層合板在靜平衡位置附近剛度接近于零。在外太空環境中可以忽略被隔振設備自重,所以可以考慮單獨利用此狀態的層合板作為準零剛度機構進行衛星微振動低頻隔振,此時層合板穩定構型為馬鞍面構型,靜平衡狀態角點面外位移為零。從力位移關系曲線圖還可以發現,當系統偏離平衡位置達到一定位移后,系統承載能力顯著增加,具體數據見表格3,可以在衛星發射階段承受過載,保護系統在衛星發射階段不被損壞。傳統的線性隔振系統顯然無法同時起到在太空中低頻隔振,以及發射階段承受過載的作用。
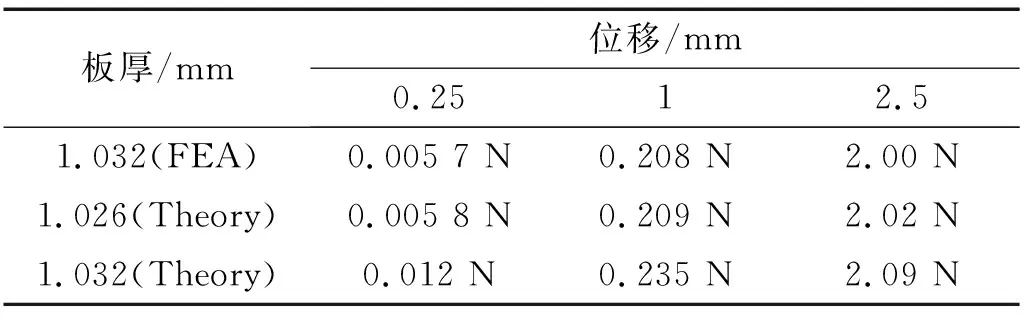
表3 不同位移下系統反作用力對比Tab.3 Refraction force of different displacement
3.1 隔振效果研究
首先利用理論和有限元方法研究層合板無阻尼自由振動頻率,層合板中心固定,四個角點各固定一個重量為50 g的質量塊,在四個角點施加集中載荷,撤去載荷后層合板無阻尼振動頻率與預作用力的關系曲線如圖7所示。從圖7可發現層合板無阻尼自由振動頻率隨角點預作用載荷增大非線性的增大,即層合板剛度隨著角點偏離平衡位置的位移增大而非線性增大,與圖5(d)所示結果相符。
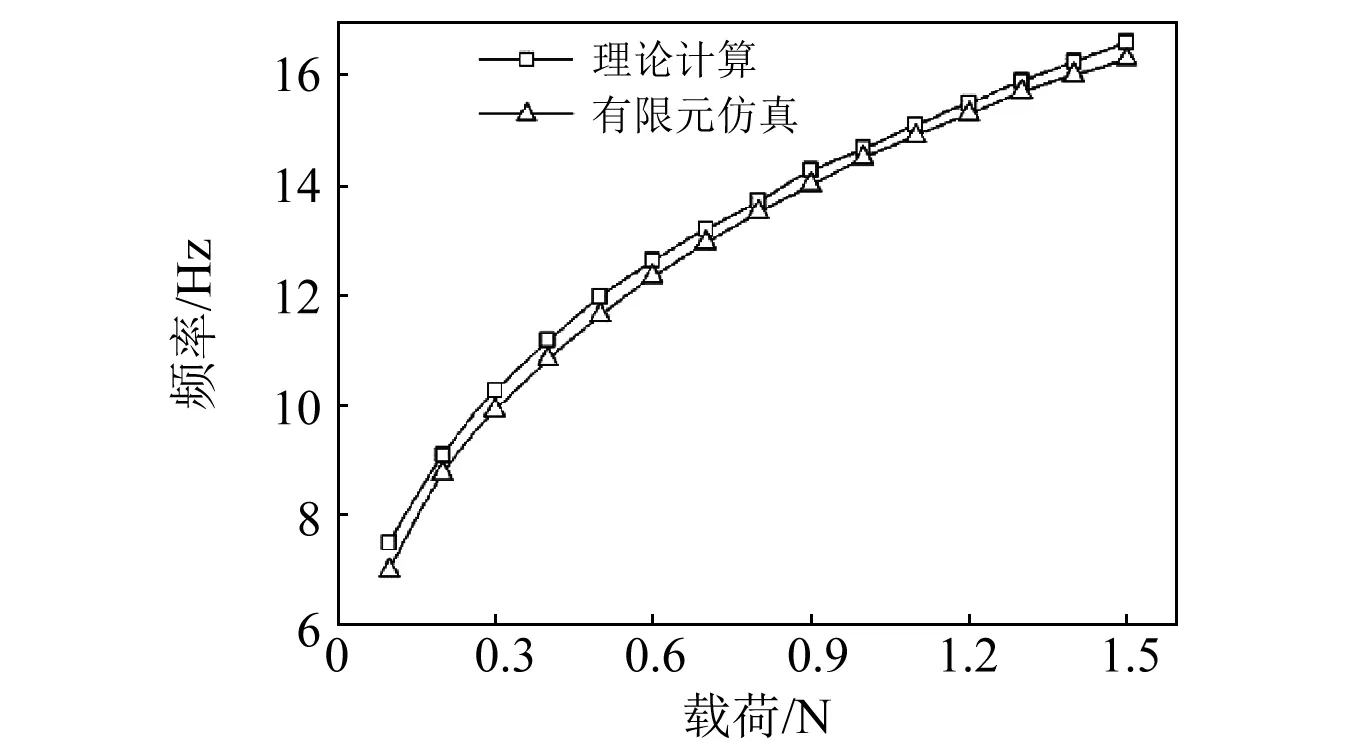
圖7 層合板無阻尼自由振動頻率Fig.7 Nature frequency of laminate
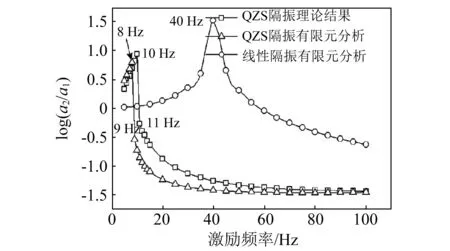
在厚度為1.032 mm的復合材料層合板四個角點各固定一個質量塊,構成簡單隔振系統。在層合板中心施加正弦加速度激勵如式(29)所示。激勵加速度幅值為a1=50 mg,層合板質量阻尼系數取100。觀測角點加速度響應,角點加速度響應幅值記為a2,將得到的結果與相同材料的由無殘余熱應力的正交鋪設平板構成的線性隔振系統的隔振效果進行比較,結果如圖8所示。
a=a1sin(2πft)
(29)
(a)角點質量4×25 g

(b)角點質量4×50 g圖8 激勵頻率對加速度傳遞幅值的影響Fig.8 Excitation frequency effect
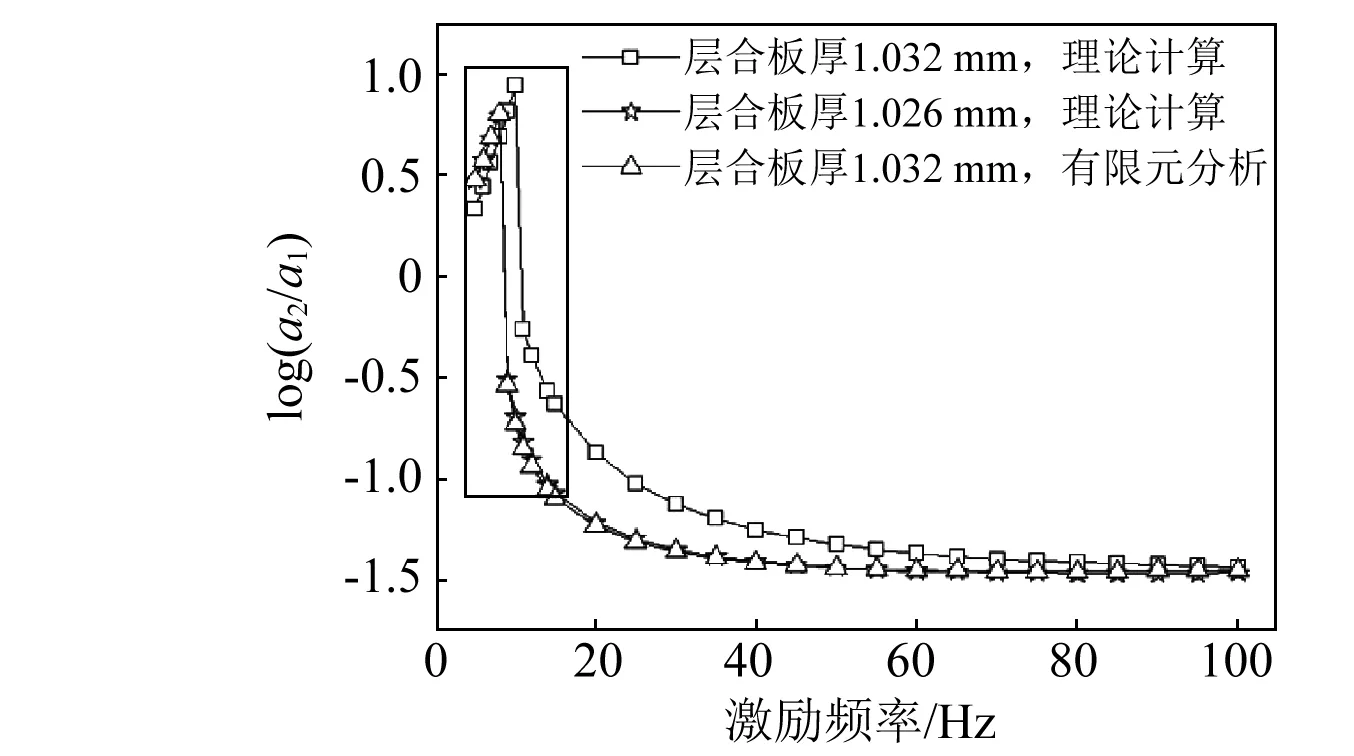
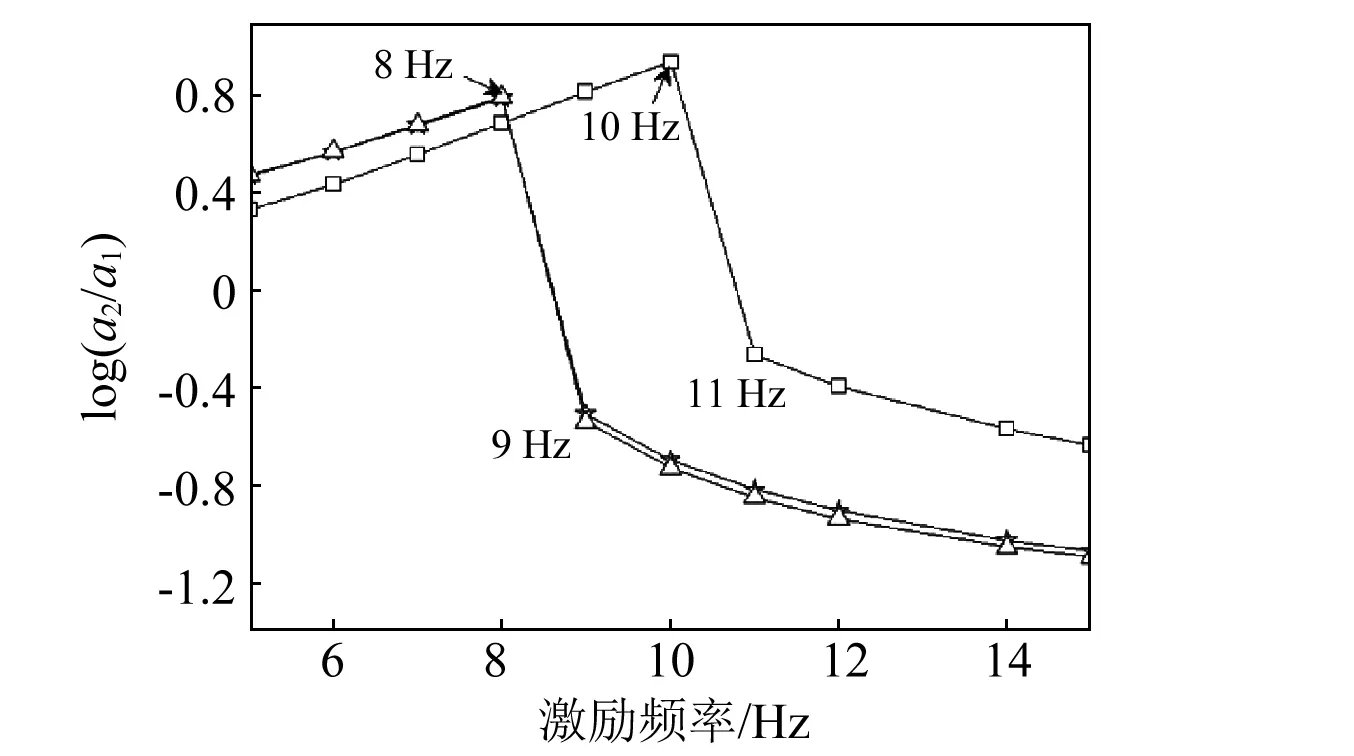
由圖8可以發現隨著被隔振設備質量的增加,系統固有頻率降低,本文研究的準零剛度系統理論計算結果與有限元分析結果在一定頻帶范圍內兩者存在較大誤差,但總的隔振效果隨激勵頻率的變化趨勢一致。與線性隔振系統相比,準零剛度系統的固有頻率低于線性隔振系統,振動加速度傳遞峰值小于線性隔振系統,隔振有效區域寬于線性隔振系統,且在隔振有效頻帶內隔振效果明顯優于線性隔振系統。
3.2 誤差分析及討論
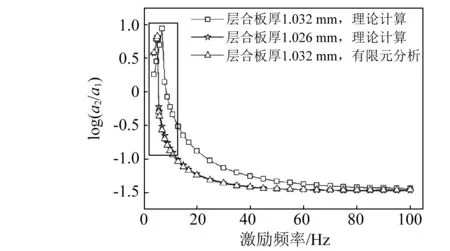
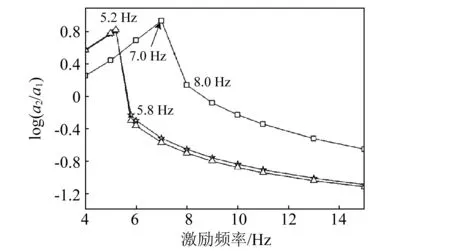
由圖8發現理論模型計算結果與有限元分析結果存在一定誤差,產生誤差的主要原因是理論模型中取層合板的厚度為1.032 mm,由圖6中力位移關系曲線可以發現此時理論模型在平衡位置附近剛度遠大于有限元模型,圖9中給出了理論模型利用厚度為1.026 mm層合板的隔振效果。角點質量為4×25 g。
圖9中結果顯示當理論計算模型中層合板厚度取1.026 mm時,其隔振效果與有限元模型吻合較好,與圖6結果相符。圖9中結果顯示被隔振設備質量確定時,加速度激勵幅值增加會導致系統固有頻率增加,如本研究中對于重100 g的被隔振設備,激勵加速度幅值有10 mg增加到50 mg時,系統固有頻率有5.2 Hz增加到8 Hz。原因是系統剛度隨系統偏離平衡位置位移增大而增大。
(a)激勵幅值10 mg
(b)激勵幅值10 mg局部圖
(c)激勵幅值50 mg
(d)激勵幅值50 mg局部圖圖9 隔振效果對比Fig.9 Contrast of isolation effect
通過與文獻[7-8]中研究結果對比發現,本文研究的隔振器與傳統準零剛度隔振器隔振效果類似,但具有結構簡單的優勢,有利于衛星減重設計。
4 結 論
本文建立了正交鋪設復合材料層合板的理論模型,研究了其雙穩定特性以及剛度特性層板厚度之間的關系,發現隨著層合板厚度增加其負剛度變形區間逐漸變窄,當層合板厚度達到失去雙穩定特性臨界厚度時,層合板具有準零剛度特性。研究了以該厚度層合板作為準零剛度機構進行隔振的效果,通過與線性隔振系統的隔振效果進行比較發現,該準零剛度隔振系統具有固有頻率低、隔振頻帶寬、在隔振頻帶范圍內隔振效果好等優點。且與傳統準零剛度隔振機構相比,本文研究的準零剛度隔振系統結構簡單,占用空間小,無需復雜的機構便可以實現準零剛度特性,對于衛星微振動隔離具有潛在應用價值。

