基于余量諧波平衡法的質點振動系統高階近似與頻率響應分析

國忠金， 張 偉， 夏麗莉

(1. 泰山學院 數學與統計學院，山東 泰安 271000；2.北京工業大學 機電學院，北京 100124；3. 機械結構非線性振動與強度北京市重點實驗室， 北京 100124)

非線性動力學與振動分析對機械、結構動力學問題研究是非常重要的，它能夠全面了解和準確預測系統運動特性。近年來，旋轉拋物線上的質點運動系統引起了廣泛關注[1-2]，其控制方程為如下非線性自治微分方程

(1)

式中：△為線性剛性系數且△>0；q為非線性項系數且q>0；A為初始振幅且A>0。

針對方程(1)，文獻[3]運用同倫與攝動耦合方法，文獻[4]利用改進的迭代攝動法，文獻[5]運用能量平衡法、同倫攝動法、振幅-頻率公式以及微分變換法，文獻[6]運用哈密爾頓法，文獻[7]運用變分法，文獻[8]運用優化同倫分析方法獲得了其穩態下的振動頻率。一方面，以上文獻給出的近似振動頻率與精確結果之間存在一定的誤差，其近似精度有待提高。另一反面，攝動方法適用于弱非線性系統，對系統穩態下的振動頻率隨系統參數尤其是非線性項系數變化的振動特性還需進一步研究。

諧波平衡方法是不受小參數約束應用最廣泛的定量分析方法。文獻[9]應用諧波平衡法計算了一個恢復力與因變量成反比的非線性振子的近似頻率和近似周期。文獻[10]基于諧波平衡法研究了擺線鋼球行星傳動系統的基頻穩態響應及動態特性。諧波平衡對于一階近似解求解很方便，但精度不高。因此，許多研究者將諧波平衡法進行了一些推廣，發展了一些諸如增量諧波平衡[11]、攝動-增量[12]、牛頓諧波平衡[13]、余量諧波平衡[14]、多層余量諧波平衡[15]等方法。余量諧波平衡引入階層參數，融合同倫思想到諧波平衡方法中，繼而余量延拓，易獲得高階近似解。

本文針對旋轉拋物線上的質點運動系統構建了其振動頻率、穩態響應求解的余量諧波平衡解程序，得到系統的高階余量諧波平衡近似，并與已有文獻結果進行比較分析。進而研究了系統初始振幅、非線性項系數等參數對系統非線性振動頻率特性的影響。

1 余量諧波平衡解程序

假定ω是方程(1)的未知振動角頻率，引入變量τ=ωt，得

(2)

基于方程(2)的對稱性，其周期解具有如下基本解級數形式

{cos[(2k+1)]|k=0,1,2,…}

(3)

為方便計算，引入階層參數p，并將系統穩態下解響應及振動頻率設為

(4)

式中：ωi(i=0,1,2,…)為未知頻率。

1.1 初始諧波近似

根據方程(2)初始條件，初始諧波解為如下形式

u0(τ)=Acos(τ),τ=ω0t

(5)

將式(5)代入式(2)，得初始余量項

(6)

根據伽遼金法，消除久期項，易獲得初始諧波近似頻率及周期響應為

(7)

式(7)近似公式與同倫與攝動耦合方法、改進的迭代攝動法、能量平衡法、同倫攝動法、振幅-頻率公式、哈密爾頓解法、變分法等方法近似結果一致。

1.2 1 階余量諧波近似

將初始近似式(7)代入余量項式(6)時，系數非零。因此，我們將式(4)代入(2)合并階層參數的一次系數，得

(8)

式(8)為關于未知ω1和u1(τ)的線性方程，根據周期解級數形式(3)及初始條件，假定

u1(τ)=a3,1[cos(τ)-cos(3τ)]

(9)

將式(9)代入式(8)，并消除初始余量項，得

R1(τ)=Г1(τ)+R0(τ)=

(10)

將初始余量項引入式(10)，提高解的精確性。根據伽遼金法，消除久期項，我們解cos(τ)和cos(3τ)的系數方程得1-階余量諧波近似為：

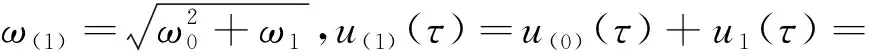
(11)

1.3 2 階余量諧波近似

將1-階余量諧波近似式(11)代入余量項式(10)時，cos(5τ)系數非零。因此，我們將式(4)代入式(2)合并階層參數p的2次系數，得

(12)

式(12)為關于未知ω2和u2(τ)的線性方程，根據周期解級數形式(3)及初始條件，假定

u2(τ)=a3,2[cos(τ)-cos(3τ)]+a5,2[cos(τ)-cos(5τ)]

(13)

將式(13)代入(12)式，并消除1-階余量項，得

(14)

根據伽遼金法，消除久期項，我們解cos(τ)，cos(3τ)和cos(5τ)的系數方程得2-階余量諧波近似為：

(A+a3,1+a3,2+a5,2)cos(τ)-(a3,1+a3,2)cos(3τ)-

a5,2cos(5τ),τ=ω(1)t

(15)

1.4 高階余量諧波近似

類似于上述求解過程，一般地，k-階余量諧波近似

u(k)(τ)=u(k-1)(τ)+uk(τ),

u(k-1)(τ)=u(k-2)(τ)+uk-1(τ),

u(0)=Acos(τ),ω(0)=ω0,k=2,3,4,…

(16)

2 結果分析與討論

本部分給出了實例討論了文中所給出結果的有效性，并圖解了非線性項系數，線性剛度系數，初始振幅-頻率曲線以及初始振幅、非線性項系數的影響。

2.1 近似解析解比較

通過積分方程(1)，其精確振動頻率為

(17)

表1給出了已有文獻[3-7]結果與本文2-階余量諧波近似結果的比較，其中相對誤差定義為：

(18)

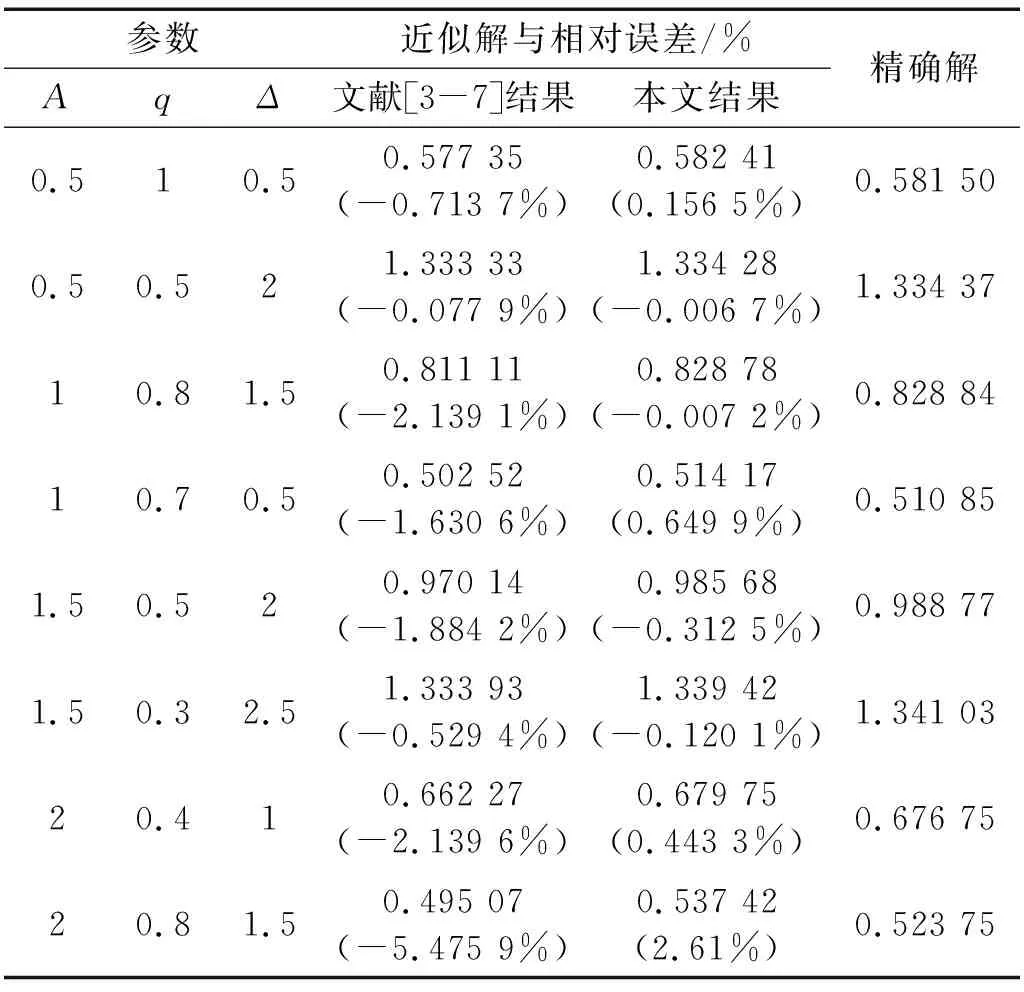
表1 余量諧波平衡解頻率及其相對誤差與已有文獻和精確解結果的比較Tab.1 The Residue harmonic balance frequency and relative error presented here with result comparison from other references and exact solution

從表1可以看出，本文給出的近似振動頻率結果比已有文獻：同倫與攝動耦合方法、改進的迭代攝動法、能量平衡法、同倫攝動法、振幅-頻率公式、變分法、哈密爾頓法等方法在各類參數下結果更加精確，與精確解的相對誤差大大降低。

為了進一步圖解本文結果的有效性，圖1，2顯示了不同參數下系統的時域振幅曲線比較。其中，圖1近似解析表達如下：

文獻[3-7]近似為：u(t)=cos(0.811 1t)

本文2-階余量諧波平衡近似：

u(t)=1.058 7 cos(0.828 78t)-0.076 7 cos(2.486 3t)+0.017 95 cos(4.143 9t)

圖2近似解析表達如下：

文獻[3-7]近似為：u(t)=2 cos(0.662 27t)

本文2-階余量諧波平衡近似：

u(t)=2.114 6 cos(0.679 75t)-0.150 2 cos(2.039 3t)+0.035 55 cos(3.398 7t)

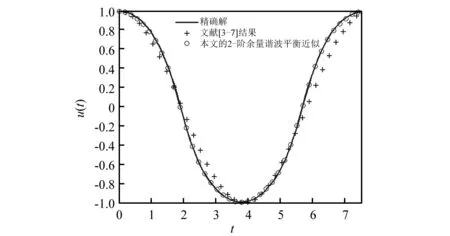
圖1 解析近似解與精確解比較當q=0.8,Δ=1.5與A=1 Fig.1 Comparison of analytical solution u(t) with the exact one for case q=0.8，Δ=1.5 and A=1

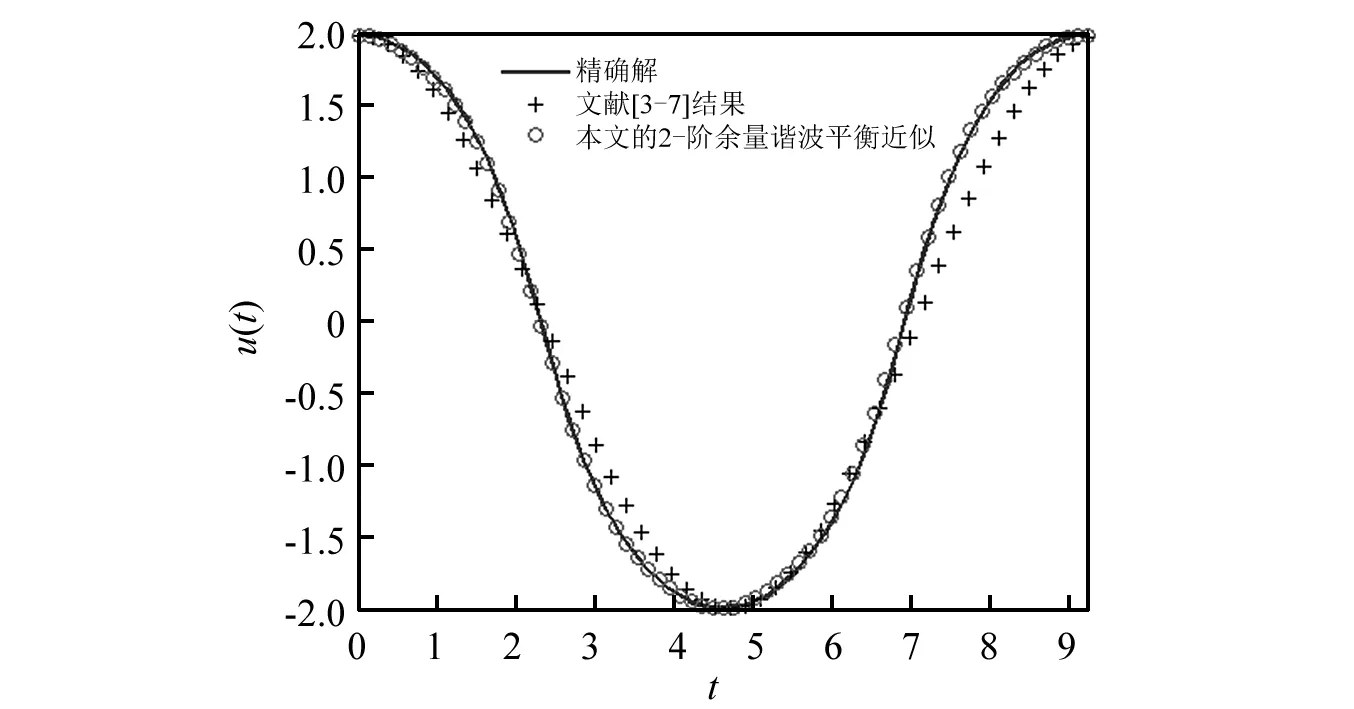
圖2 解析近似解與精確解比較當q=0.4,Δ=1.5與A=2 Fig.2 Comparison of analytical solution u(t) with the exact one for case q=0.4，Δ=1 and A=2

2.2 非線性項系數q-頻率曲線及其初始振幅影響

以Δ=1.5為例，圖3圖解了非線性項系數-振動頻率曲線及其初始振幅的影響。其中圈線為本文所給出的2-階余量諧波近似，實線為精確值。從圖3可以看出，隨著系統非線性項系數q的增大，振動頻率逐漸減小，初始振幅越大，其相應的振動頻率越小。并且本文獲得的高階解析近似結果與精確值吻合的相當好。

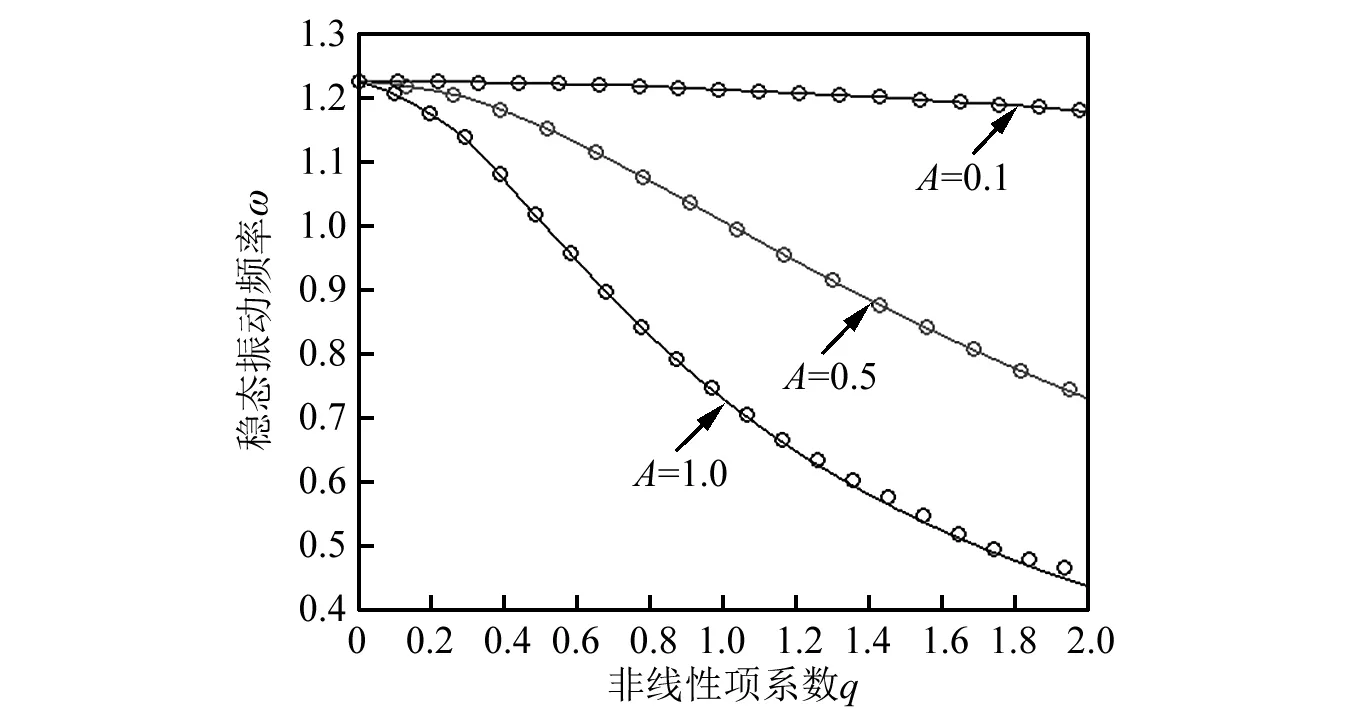
圖3 非線性項系數q與振動頻率曲線及其比較Δ=1.5，其中“o” 線表示本文的2-階余量諧波平衡近似，實線為精確結果。Fig.3 Comparison of vibration frequency corresponding to nonlinear parameter q and Δ=1.5.“o” lines denotes the presented second-order residue harmonic balance approximations, solid lines are exact ones.

2.3 初始振幅A-頻率曲線及其非線性項系數影響

以Δ=2為例，圖4圖解了初始振幅-振動頻率曲線及其非線性項系數的影響。其中圈線為本文所給出的2-階余量諧波近似，實線為精確值。從圖4可以看出，隨著初始振幅A的增大，振動頻率逐漸減小。在其他參數不變條件下，非線性項系數越大，其相應的振動頻率越小。并且本文獲得的高階解析近似結果與精確值吻合的比較一致。

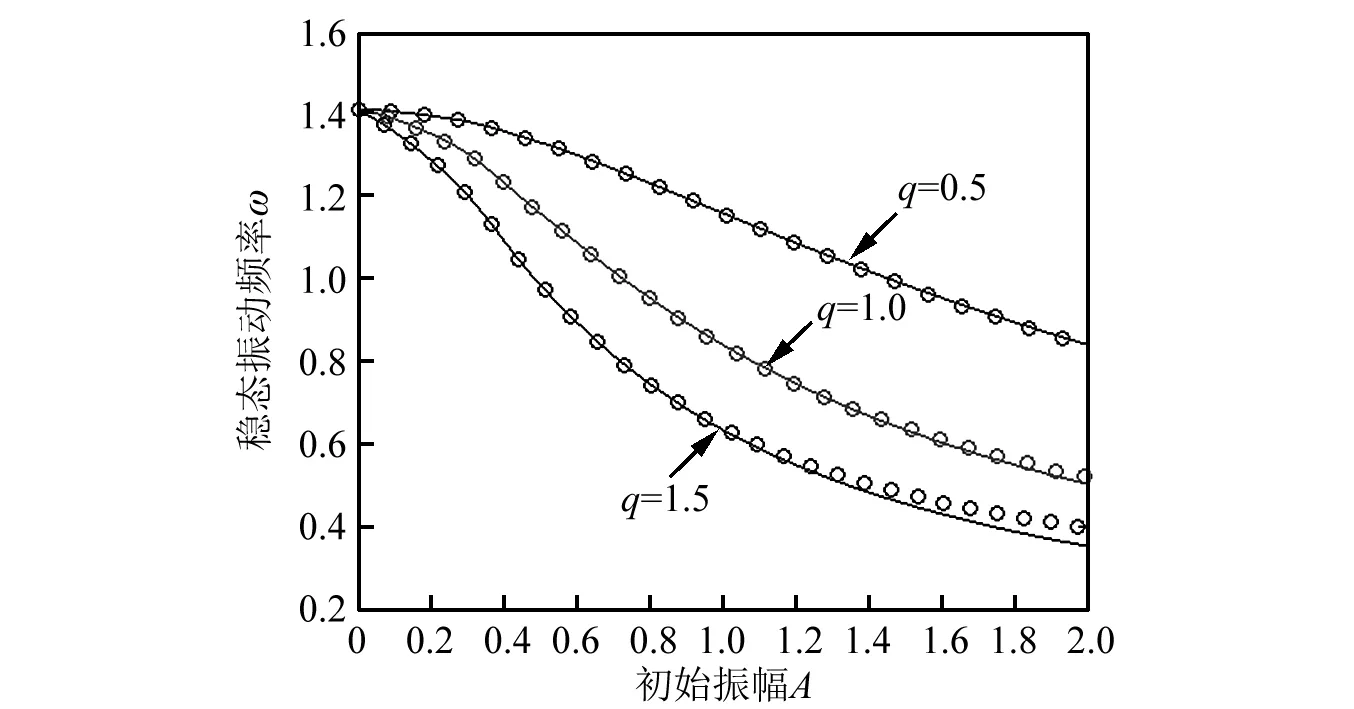
圖4 初始振幅A與振動頻率曲線及其比較Δ=2，其中“o” 線表示本文的2-階余量諧波平衡近似，實線為精確結果。Fig.4 Comparison of vibration frequency corresponding to initial amplitude A and Δ=2.“o” lines denotes the presented second- orderresidue harmonic balance approximations, solid lines are exact ones.

2.4 線性剛性系數-頻率曲線及其非線性項系數影響

以A=0.5為例，圖5圖解了線性剛度系數-振動頻率曲線及其非線性項系數的影響。其中圈線為本文所給出的2-階余量諧波近似，實線為精確值。從圖5可以看出，隨著線性剛度系數Δ的增大，振動頻率逐漸增大。在其他參數不變條件下，非線性項系數越大，其相應的振動頻率越小。并且本文獲得的2-階余量諧波解析近似結果與精確值保持一致。

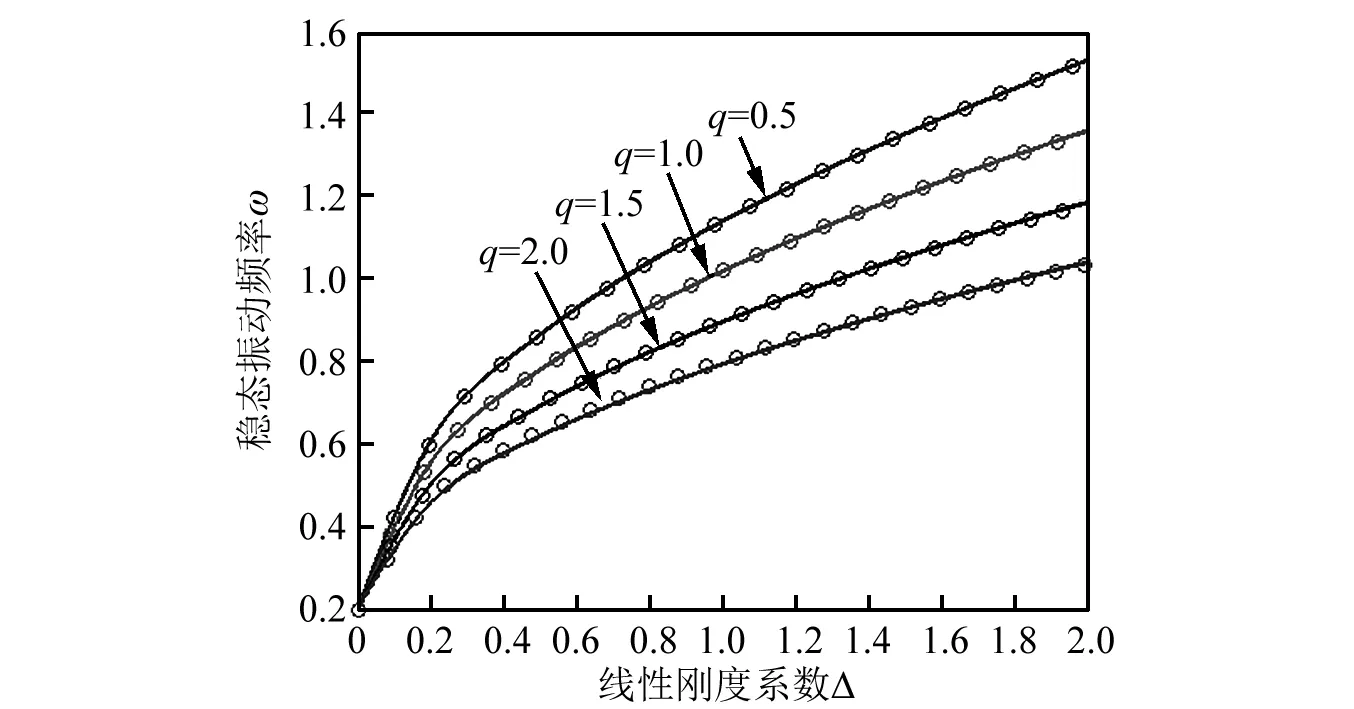
圖5 線性剛度系數與振動頻率曲線及其比較A=0.5，其中“o” 線表示本文的2-階余量諧波平衡近似，實線為精確結果。Fig.5 Comparison of vibration frequency corresponding to linear stiffness coefficient Δ and A=0.5. “o” lines denotes the presented second-order residue harmonic balance approximations, solid lines are exact ones.

3 結 論

本文基于諧波平衡方法，發揮同倫思想的優勢，構建了不含小參數,適用于求解非線性自治振動系統高階近似的余量諧波平衡解程序。解程序在每一階近似中均消除了上一階的諧波余量，高階近似表達僅需初始諧波近似，不需根據前一階近似進行調整。理論上，任何精度的高階近似均能依次獲得。

將方法運用到旋轉拋物線上質點運動方程中，我們可以看到

(1)本文獲得的2-階余量諧波平衡近似振動頻率比已有的變分法、哈密爾頓法、同倫與攝動耦合方法等結果更加精確，與精確值的相對誤差在不同參數下均大大降低。本文獲得的高階解析近似結果與精確值吻合的相當好。

(2)系統穩態下的振動頻率隨系統非線性項系數的增大而逐漸減小，并且初始振幅越大，其相應的振動頻率越小。

(3)系統穩態下的振動頻率隨初始振幅A的增大而逐漸減小，并且非線性項系數越大，其相應的振動頻率越小。

(4)系統穩態下的振動頻率隨線性剛度系數Δ的增大而逐漸增大，并且非線性項系數越大，其相應的振動頻率越小。