纖維鋪層角度對復合材料薄壁圓管軸向壓潰吸能特性影響研究

解 江， 馬驄瑤， 霍雨佳， 周 建， 牟浩蕾, 馮振宇

(中國民航大學 民航民用航空器適航審定技術重點實驗室， 天津 300300)

由于具有比模量高、比強度大、質量輕及優異的吸能特性等，復合材料自20世紀80年代開始在航空航天領域得到廣泛應用[1]。近年來，碳纖維增強樹脂基復合材料在民用航空器中的應用比例越來越大，尤其是大量應用到機身這樣的主承力結構上，如波音787和空客A350。由于復合材料結構與金屬結構在失效模式和墜撞吸能機理上的顯著不同，復合材料結構的使用為航空器結構適墜性設計、驗證及適航審定帶來了極大的技術挑戰。

以民用運輸類飛機為例，當發生應急著陸或墜撞時，飛機客/貨艙地板下部結構能起到緩沖吸能的作用，以減少傳遞給機上乘員的載荷并保證客艙結構完整性，從而確保乘員的生命安全[2]。目前民用運輸類飛機客/貨艙地板下部主要采用重量輕、剛度高的典型薄壁結構，如果突破復合材料的失效吸能機理和設計技術，復合材料薄壁結構具備成為一種高效吸能結構的潛力，從而保證航空器的墜撞安全。2005年開始，波音公司對B787復合材料機身框段結構進行墜撞分析與設計，并從2007年起，對B787機身結構進行了3次實驗：客艙地板下部結構的壓縮實驗；客艙地板下部結構倒置沖擊實驗；3 m長的機身下部結構9.14 m/s的墜撞實驗。同時，FAA聯合華盛頓大學等，針對B787機身下部復合材料緩沖吸能結構也開展了大量的試驗方法、分析方法與吸能結構優化研究[3-6]。為B787下部結構的適墜性設計提供了重要依據。

與此同時，國內外學術界對薄壁吸能結構的吸能機理及吸能特性也進行了深入研究。Farley[7]通過壓潰試驗證明復合材料吸能能力是金屬材料的5倍～10倍。Kindervater[8]對不同截面形狀的復合材料管件吸能特性進行研究，發現方管的比吸能低于圓管，前者為后者比吸能的0.5倍～0.6倍。Farley[9]和Keal[10]研究了玻璃纖維/聚酯樹脂圓管隨纖維鋪層角度改變對比吸能的影響，研究發現，對該材料而言，當纖維鋪層角度小于65°時，比吸能與鋪層角度成正比，高于65°時比吸能與鋪層角度成反比。Hull等[11]研究了[±θ]鋪層成型的玻璃纖維增強聚酯基圓管，發現鋪層角度在35°～65°范圍時，吸能能力隨著角度增大而增加，在65°～90°范圍時吸能能力隨著角度的增大而降低。另外，國內部分研究機構及學者也針對薄壁吸能結構(圓管、方管、波紋板、復合材料增強鋁管等)的吸能特性做了大量研究[12-18]。考慮到影響復合材料圓管破壞行為的因素多且復雜，需要進一步深入研究其吸能特性，進而為薄壁吸能結構設計及有限元建模提供支持。

本文針對典型航空碳纖維增強樹脂基復合材料體系，考查復合材料薄壁圓管在軸向壓縮載荷下的破壞吸能特性。采用LS-DYNA中的54號增強復合材料損傷模型建立了復合材料薄壁圓管有限元模型，通過對比峰值載荷及比吸能等，驗證了復合材料圓管有限元模型和分析方法，基于驗證的有限元方法，分析不同纖維鋪層角度對復合材料薄壁圓管軸向壓潰吸能特性的影響規律。

1 試驗研究

本文研究的碳纖維增強的樹脂基復合材料為T700/3234，其中碳纖維含量為64.3%。按照GBT1447—2005、GBT1448—2005、GBT1450.1—2005、HB7402—1996開展材料力學性能測試，獲得T700/3234的主要力學性能參數,如表1所示。

復合材料薄壁圓管試驗件由12層T700碳纖維增強環氧樹脂層合而成，鋪層角度為[±45/0/0/90/0]s，試驗件高度L=100 mm，內徑為D=50 mm，厚度t=1.5 mm，頂端采用45°外倒角進行削弱，從而降低初始峰值載荷便于誘導圓管發生漸進壓潰，試驗件如圖1所示。圖中θ為纖維方向與圓管軸線的夾角，本文將θ角定義為復材圓管的鋪層角度。

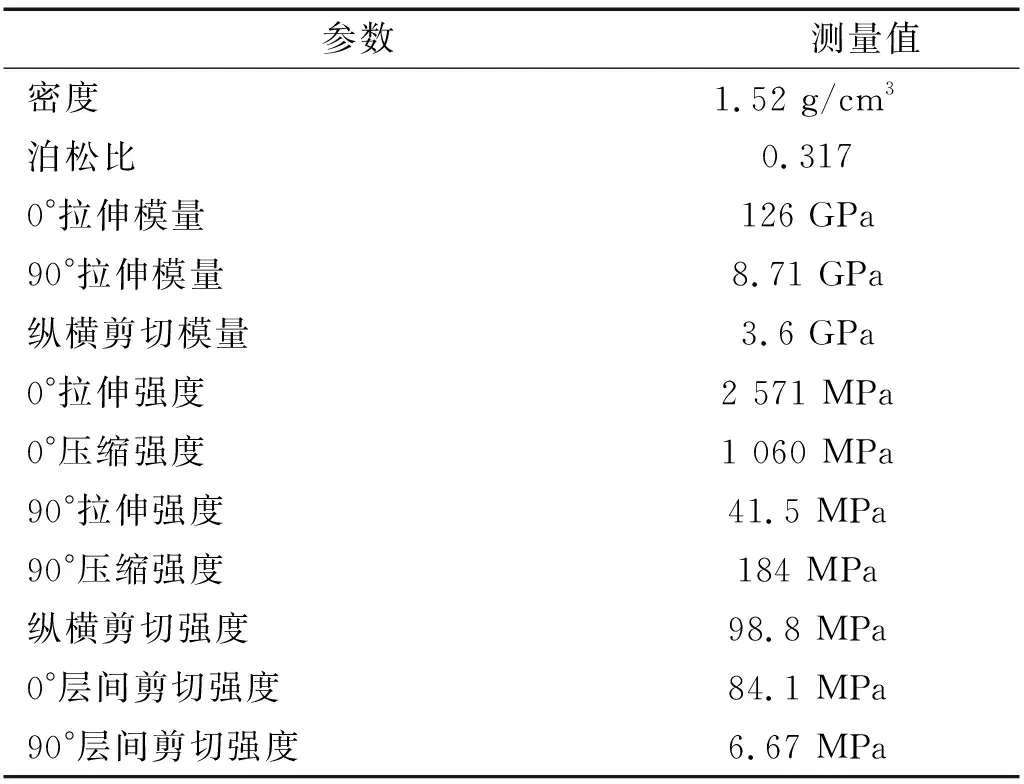
表1 T700/3234力學性能Tab.1 Mechanical properties of T700/3234

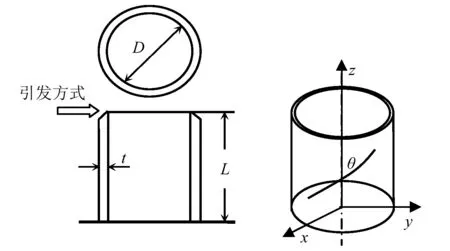
圖1 試件外形幾何尺寸Fig.1 Specimen dimension diagram

本文主要采用比吸能、峰值載荷、平均壓潰載荷和載荷效率等指標對吸能特性進行定量分析。這些指標的具體定義如下：

(1)比吸能(Specific Energy Absorption,SEA)是指在有效破壞長度(l)內，結構單位質量(m)吸收的總能量(EA)，是衡量元件吸能能力的重要參數。在壓潰過程中結構所吸收的總能量可由壓潰力(F)在壓潰距離上的積分得到。

(1)

式中：ρ為材料密度；A為薄壁管有效橫截面積。

(2)峰值載荷(Fmax)是結構被壓潰破壞的門檻值，用于評價結構在外力作用下發生破壞吸能的難易程度，是載荷-位移曲線的初始峰值。

(3)平均壓潰載荷(Fmean)是整個壓潰過程的載荷平均值。

(2)

式中:F為壓潰載荷;s為壓潰位移;S為整個壓潰過程的壓潰總位移。

(4)載荷效率(AE)是平均壓潰載荷(Fmean)與峰值載荷(Fmax)的比值。

(3)

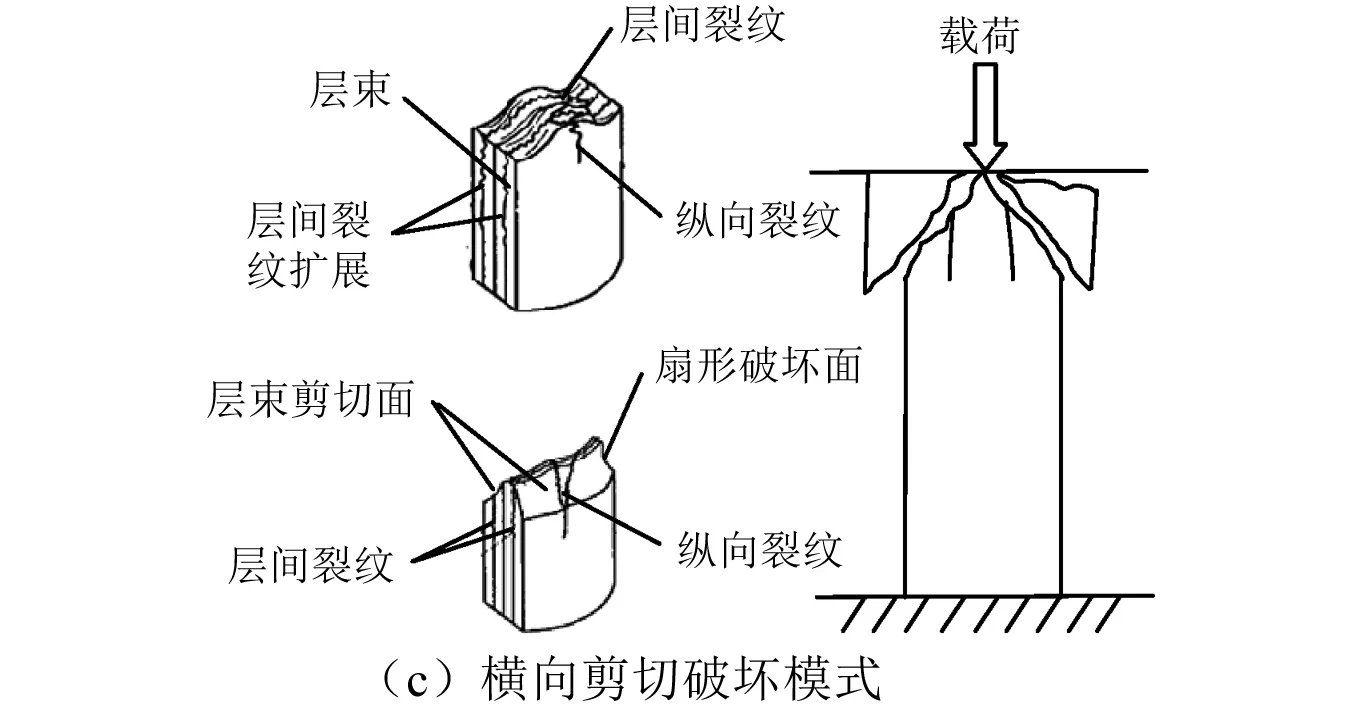
圖2 試件壓潰試驗前后形態以及破壞模式示意圖Fig.2 Comparison of the shape before and after the test and Schematic diagram of failure mode

圖2(a)和(b)給出了鋪層角度為[±45/0/0/90/0]s的復合材料薄壁圓管壓潰前后形態。Farley等通過試驗將復合材料圓管壓潰過程歸納為橫向剪切、層束彎曲和局部彎曲等3種破壞模式。從圖2(b)中可以看出，[±45/0/0/90/0]s復合材料薄壁圓管的壓潰過程為橫向剪切破壞模式，在誘發階段，有大量短的層間裂紋和縱向層內裂紋萌發并擴展，同時分裂的層束會受到橫向剪切作用，在層束基部形成彎矩，當超過材料的拉伸強度時，層束發生斷裂，最終通過層束的斷裂和層內裂紋的擴展來吸收能量，如圖2(c)所示。對此試驗件進行了兩次重復試驗，得到兩次試驗的載荷-位移曲線如圖3所示，從圖中可以看出，兩次試驗的載荷-位移曲線變化趨勢吻合性較好。通過將兩次重復試驗的結果進行對比分析，如表2所示，可以看出，兩次試驗的峰值載荷偏差為9.14%，平均載荷的偏差為7.71%，比吸能的偏差為2.5%，考慮到復合材料力學性能和加工工藝的分散性[12-13]，試驗的重復性相對較好。

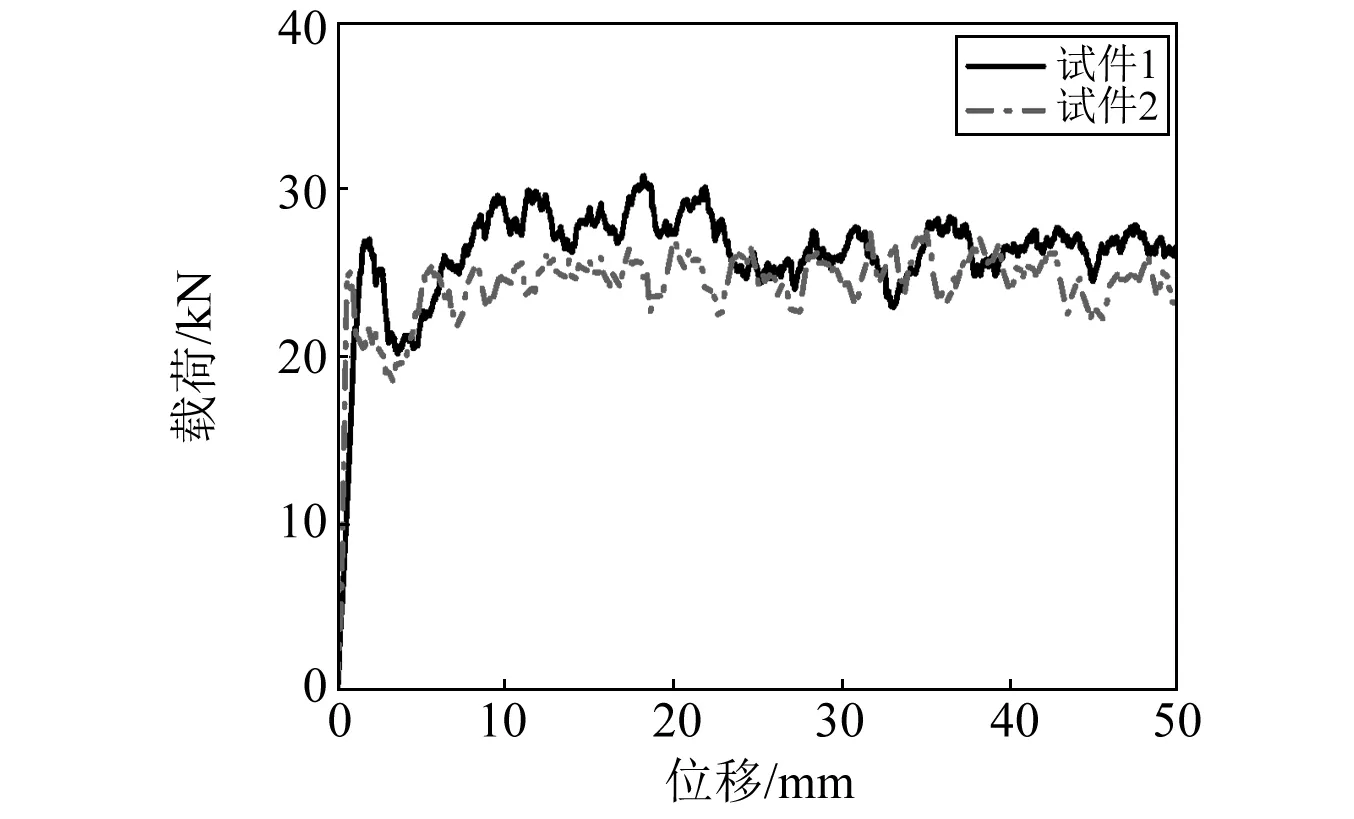
圖3 復合材料薄壁圓管準靜態壓潰載荷-位移曲線Fig.3 Experimental load-displacement curve

表2 試件1與試件2試驗數據對比Tab.2 Comparison of test data on specimen 2 and specimen 3

上述試驗件的制備、力學性能測試以及圓管的壓潰試驗均在中航工業北京航空材料研究院完成。

2 復合材料薄壁圓管有限元模型建立與驗證

2.1 有限元模型及材料參數

根據復合材料薄壁圓管試驗件尺寸，采用單層殼單元有限元建模方法，建立復合材料薄壁圓管有限元模型及剛性壓板模型。通過對殼單元厚度逐漸遞增的方式來模擬圓管頂端45°外倒角的誘發方式，如圖4所示。有限元模型采用LS-DYNA環境中的Belytschko-Tsay殼單元，54號增強復合材料損傷材料模型，T700/3234碳纖維復合材料的力學性能參數及應變失效參數如表3和表4所示。圓管上方剛性壓板采用MAT 20_Rigid剛體材料，其材料參數如表5所示。有限元模型共有4 378個殼單元，4 497個節點，圓管殼單元特征長度為2 mm。

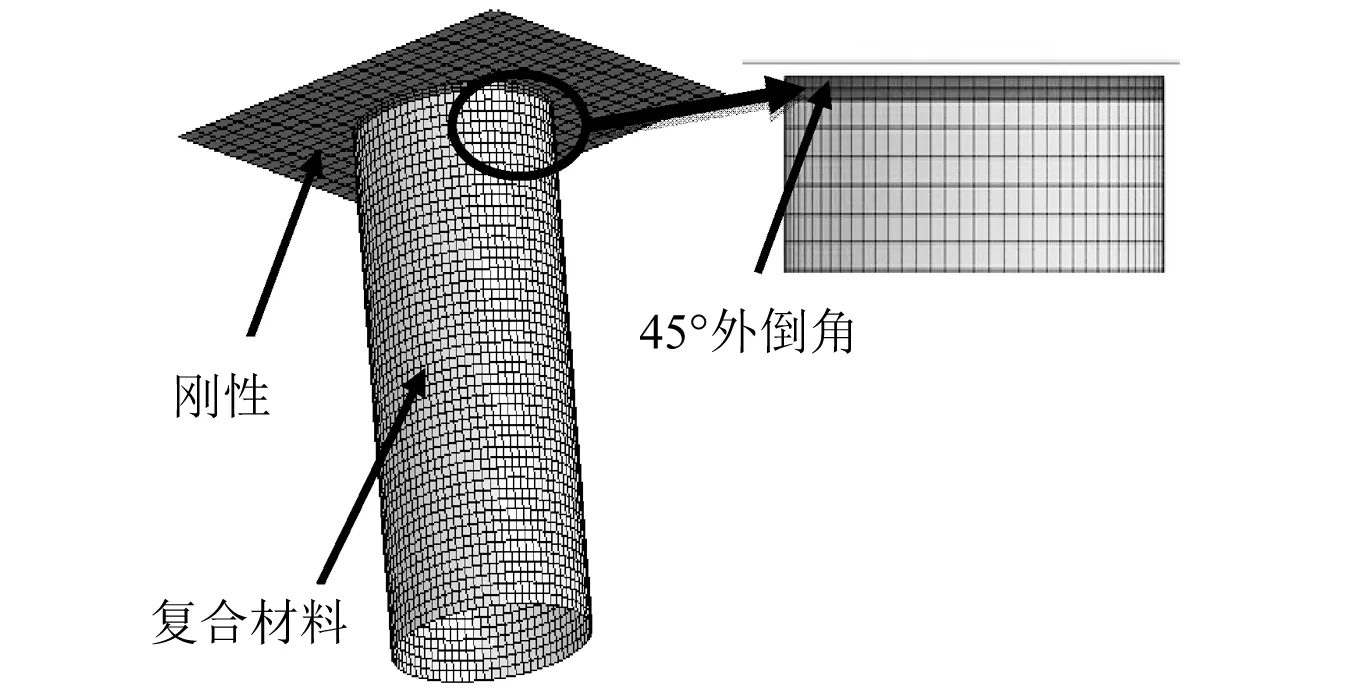
圖4 復合材料薄壁圓管有限元模型Fig.4 Finite element model of the composite tube

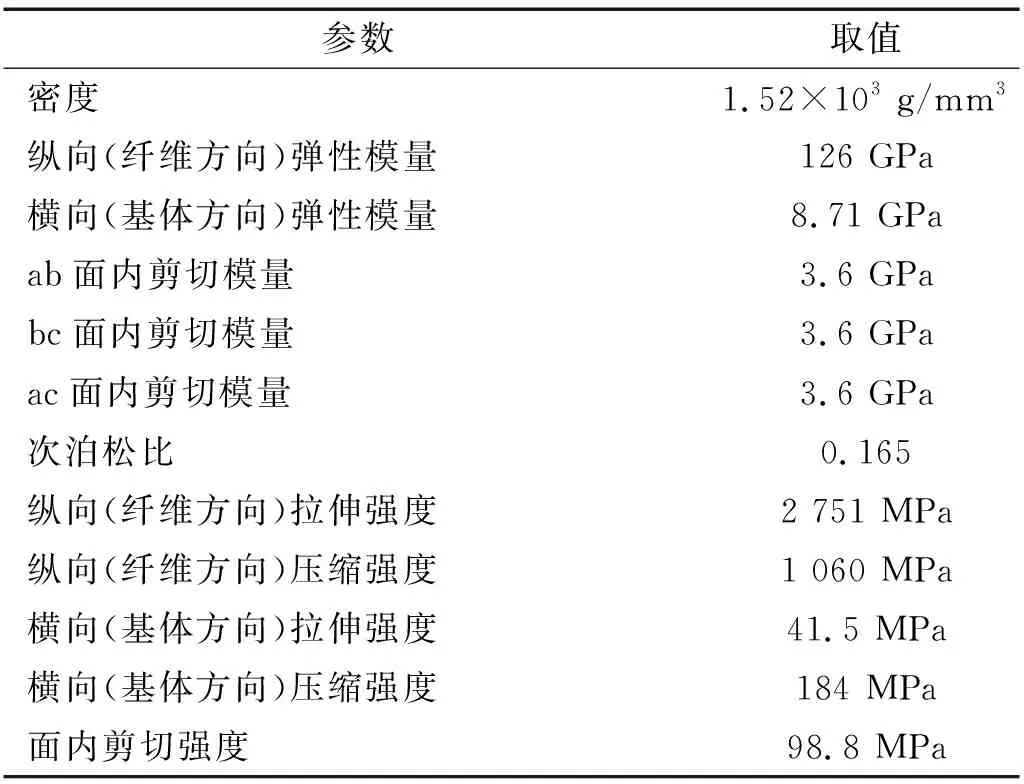
表3 T700/3234單層板的材料參數Tab.3 Material properties of the T700/3234 lamina

表4 T700/3234單層板的失效參數Tab.4 Failure parameters of the T700/3234 lamina

表5 剛性墻材料參數表Tab.5 Material parameters of rigid wall

2.2 復合材料失效準則

在LS-DYNA的54號增強復合材料損傷材料模型中[19]，材料在彈性范圍內的應力-應變關系如下：

(4)

(5)

(6)

式中:σaa為縱向(纖維方向)失效應力;εaa為縱向(纖維方向)失效應變;Ea為縱向(纖維方向)彈性模量;σbb為橫向(基體方向)失效應力;εbb為橫向(基體方向)失效應變;Eb為橫向(基體方向)彈性模量;Gab為面內剪切模量;νba為次泊松比;α是非線性剪切應力項的加權因子。當材料超出了彈性范圍，MAT54材料采用Chang-Chang準則來判定鋪層的失效行為，如方程(7)～(10)所示。

1)纖維拉伸模式(纖維斷裂)：

(7)

式中：β是在纖維拉伸模式下剪切項的加權因子，0≤β≤1.0。

當纖維斷裂引起鋪層失效后，Ea=Eb=Gab=νba=νab=0。

2)纖維壓縮模式(纖維屈曲或扭轉)：

(8)

當纖維屈曲或扭轉引起鋪層失效后，Ea=νba=νab=0。

3)基體拉伸模式(在橫向拉伸和面內剪切下的基體開裂)：

(9)

當基體開裂引起鋪層失效后，Ea=νba=0→Gab=0。

4)基體壓縮模式(在橫向壓縮和面內剪切下的基體開裂)：

(10)

當基體開裂引起鋪層失效后，Ea=νba=νab=0→Gab=0。

在上述公式中，ef、ec、em和ed稱為歷史變量，分別代表纖維方向的拉伸和壓縮強度以及基體方向拉伸和壓縮強度的變化過程。Xt是纖維方向拉伸強度，Xc是纖維方向壓縮強度，Yt是基體方向拉伸強度，Yc是基體方向壓縮強度，Sc是單向層的剪切強度。剪切應力加權因子β用于定義在拉伸失效模式下剪切行為的影響。這些輸入參數可以通過單向層合板試驗測量得到。需要注意的是文中所有參數都是假定a方向是纖維方向，b方向是基體方向，c方向是厚度方向。

2.3 邊界條件和接觸定義

復合材料薄壁圓管底端固定，頂端承受剛性壓板的軸向壓縮載荷，以5 000 mm/s的速率勻速加載。剛性壓板與圓管之間的摩擦系數設置為0.3。為防止變形過程中剛性壓板和圓管之間發生穿透，在剛性壓板和圓管之間設置點-面接觸。

2.4 模型驗證研究

圖5給出了復合材料薄壁圓管的漸進失效模式圖，可以看出圓管的失效行為表現為穩定的單元逐行消去，是一個漸進失效過程，但是單層殼單元模型不能模擬微觀的層間裂紋及層束斷裂等。從圖6的壓潰仿真與試驗的載荷-位移曲線對比圖以及表6的壓潰仿真和試驗的結果中可以看出，與試驗結果對比，仿真結果的峰值載荷偏差為7.18%，平均載荷偏差為2.14%，比吸能偏差為-4.06%，載荷效率偏差為-4.71%。仿真與試驗的載荷-位移曲線吻合度較好，從而驗證了本文建模方法及復合材料薄壁圓管仿真模型的有效性。

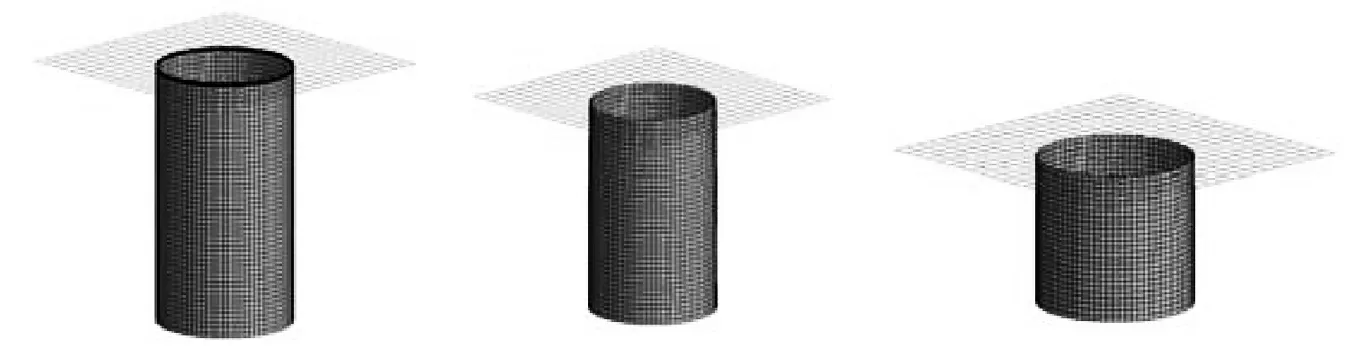
t=0 mst=4 mst=10 ms圖5 復合材料圓管潰縮過程仿真Fig.5 Compression process simulation of the thin-walled composite tube

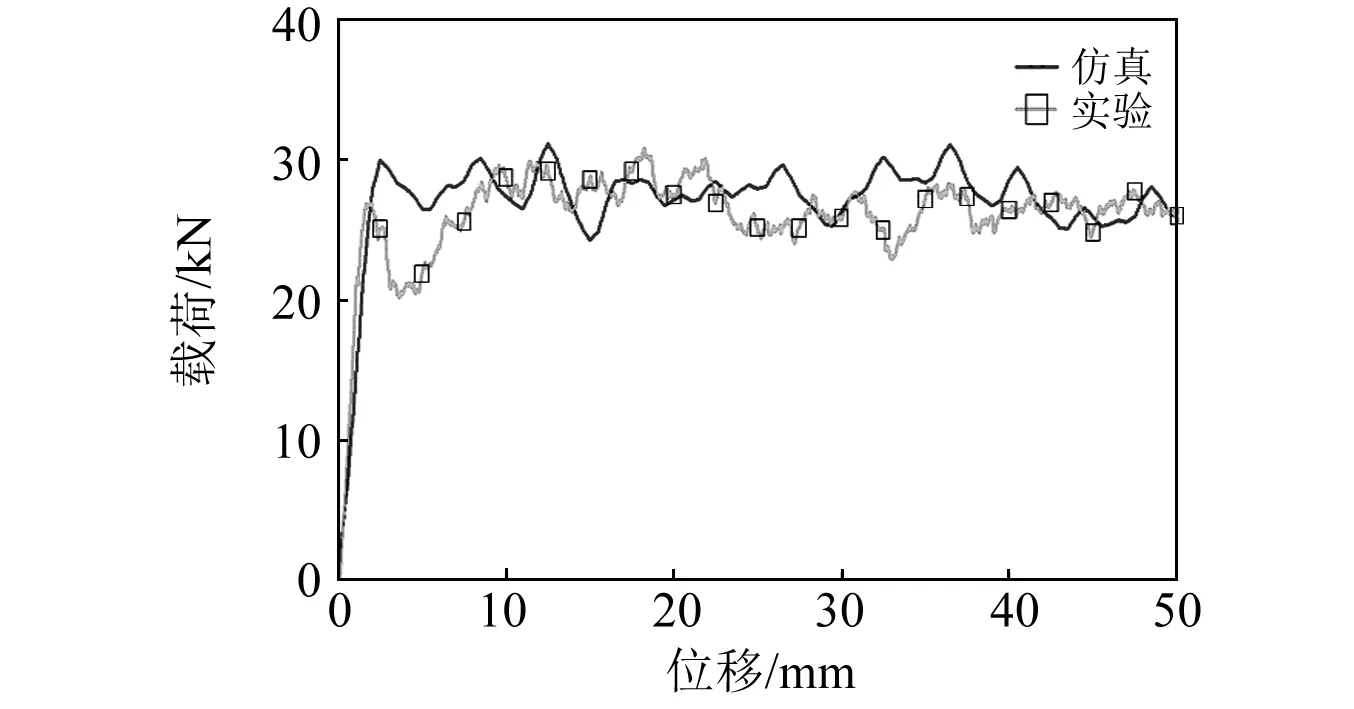
圖6 復合材料圓管軸向壓縮的載荷-位移曲線Fig.6 Load-displacement curve of the composite tube subject to axial compression

表6 仿真結果與試驗結果對比Tab.6 Comparison between experimental results and numerical results

3 不同纖維鋪層角度對圓管壓潰結果影響分析

3.1 正交各向異性材料偏軸彈性特性研究

由于復合材料具有各向異性特征，實際使用過程中，單層材料的主方向與總坐標系x-y不一致，為了在統一的x-y坐標中計算材料的剛度，需要知道單層材料的圓管結構在非主方向上的彈性系數(偏軸向彈性系數)與材料主方向彈性系數之間的關系。

工程上常采用工程彈性常數來表示材料特性，在復合材料力學研究中，常采用4個沿軸常數，分別為E1，E2，υ12，G12。本文有限元模型中所使用的材料常數如表7所示。

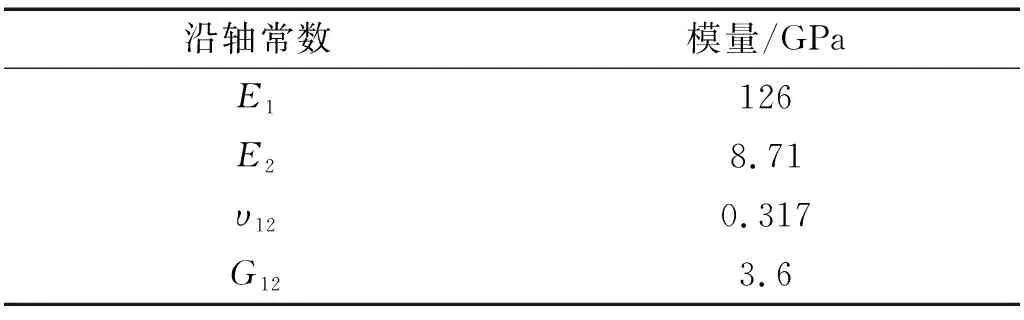
表7 有限元模型中所使用的材料常數Tab.7 The material constants used in the finite element model

按照復合材料宏觀力學基礎理論，其中偏軸彈性模量為Ex，Ey，Gxy。

(11)

(12)

(13)

在此次研究中，所采用的碳纖維增強復合材料Ex，Ey，Gxy三個偏軸工程常數隨著θ變化,如圖7所示。

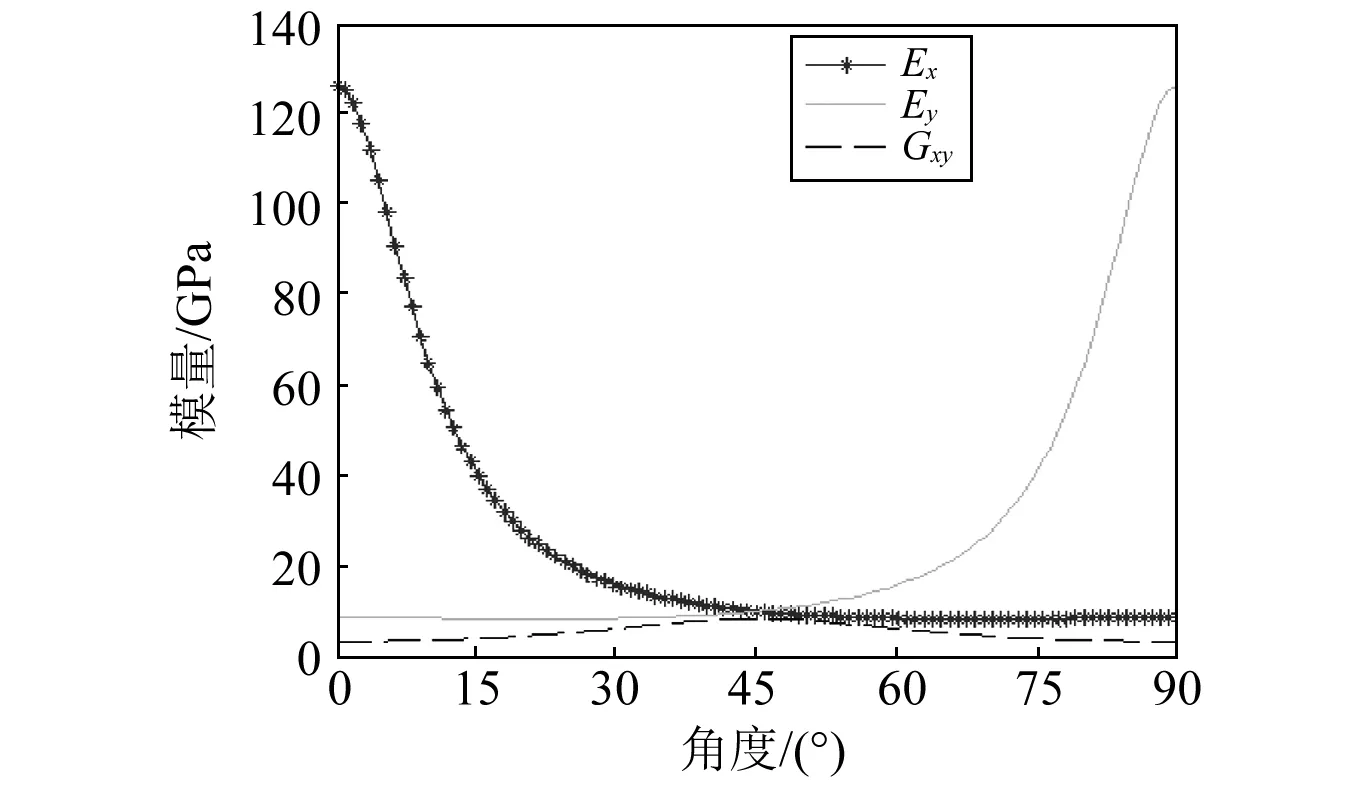
圖7 材料的偏軸工程常數與θ的關系Fig.7 Relationship between off-axis engineering constants and θ

圖中可見θ為0°時，Ex有極大值；θ為90°時，Ey有極大值；θ在為65°左右時，Ex趨于極小值。為了進一步說明曲線的趨勢，對函數1/Ex求導：

(14)

得出θ=67°。說明當鋪層角度為67°時，Ex有極小值，此時復合材料薄壁圓管沿軸向的剛度最弱，最易發生破壞吸能。通過計算反映了偏軸工程常數Ex，Ey的變化特性。而Gxy關于45°對稱分布。

3.2 不同纖維鋪層角度圓管吸能特性仿真研究

基于驗證的復合材料圓管有限元模型，考慮不同纖維鋪層角度[±15°]6、[±25°]6、[±35°]6、[±45°]6、[±55°]6、[±65°]6、[±75°]6、[±90°]6，進行軸向壓潰仿真，所用材料參數及加載工況同上，見表3～表5。

圖8是為碳纖維/環氧圓管壓潰比吸能隨纖維鋪層角度變化的規律，可見，當纖維鋪層角度從15°增加到90°，在準靜態軸向壓潰下薄壁圓管的比吸能先增大，75°之后會有一定程度減小，但比吸能值仍然相對較大。產生這一變化規律的主要原因是由于纖維鋪層角度不同，進而引起復合材料薄壁圓管軸向及徑向剛度不同，由此在軸向加載情況下導致圓管產生了不同的破壞模式。

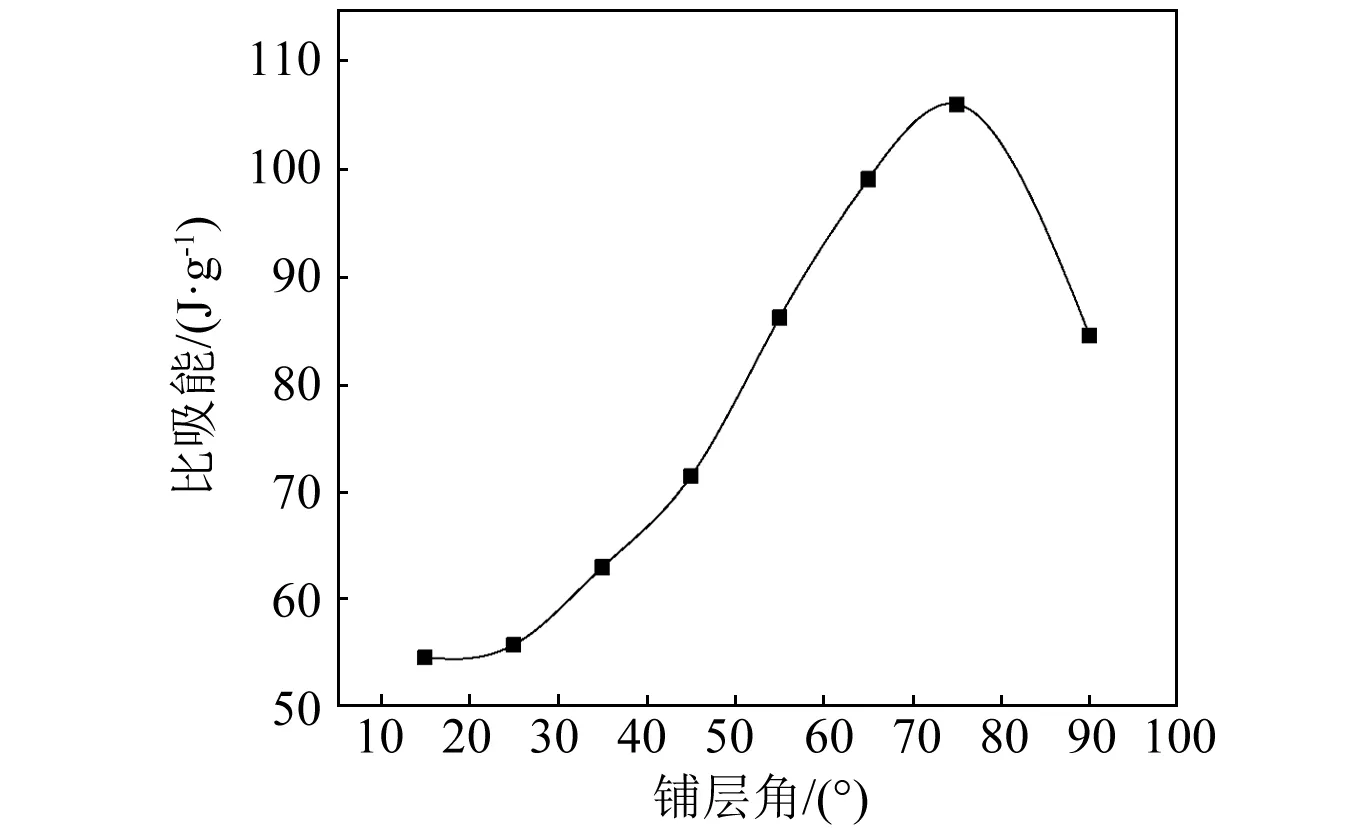
圖8 不同纖維鋪層角度對比吸能的影響Fig.8 Effect of different ply orientations on SAE

結合復合材料各向異性偏軸理論，當鋪層角度小于45°時，纖維在圓管中主要起軸向增強作用，大量裂紋首先在強度較低的周向生成，并隨著壓潰進行，管壁內大量平行纖維方向的基體裂紋在單層或相鄰層內沿纖維方向擴展，纖維鋪設角度越靠近0°，基體越容易周向開裂使纖維沿周向開裂成分離的層束，因而比吸能值越低。

當鋪層角度大于45°時，使得圓管周向剛度和強度增加，在壓潰過程中，纖維與基體共同發生作用，并且隨著鋪層角度增加，周向纖維所占比例增加，當鋪層角度為75°附近時，隨著周向的開裂，導致大量纖維被拉斷，斷裂成細小片段，從而吸收大量能量，比吸能值增大；隨后，隨著鋪層角度的增加，軸向剛度明顯減弱，圓管在壓潰過程中，容易發生失穩，導致比吸能開始減小。

另外，當結構用于緩沖吸能元件并保護乘員安全時，初始載荷峰值Fmax是能量吸收裝置關系到乘員安全的重要性能指標，若初始峰值載荷過大，乘員承受的過載可能超過人體的安全極限，從而給乘員造成一定的生命安全。由于峰值載荷具有一定的分散性，所以將峰值載荷以散點圖的形式表示，如圖9所示，可以看出，隨著纖維鋪層角度的變化，初始峰值載荷在55°左右之前，基本保持在40 kN以下，45°時峰值載荷最低。之后隨著角度的增大，初始峰值有了很大程度提高。這是因為，當纖維鋪層角度較小時，圓管的周向剛度較弱，導致圓管容易在周向開裂，并發生破壞，從而使得壓潰進程比較容易進入漸進破壞吸能階段，所以初始峰值較低。

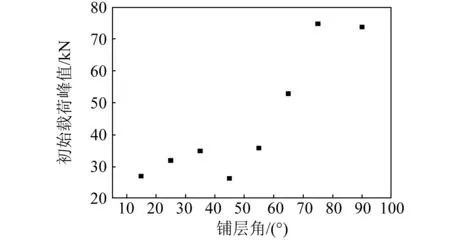
圖9 不同纖維鋪層角度對初始峰值載荷的影響Fig.9 Effect of different ply orientations on Fmax

與此同時，由于結構和空間的限制，要提高試件的耐撞性及其吸能能力，必須使其能夠持續漸進壓潰，那么，就需要盡量提高持續壓潰平均載荷Fmean。從圖10中可以明顯看出，平均壓潰載荷隨著角度的變化趨勢與圖8中比吸能的變化趨勢比較類似，這進一步說明，在壓潰過程中，壓潰平均載荷Fmean與試件的吸能能力有很大的相關性。

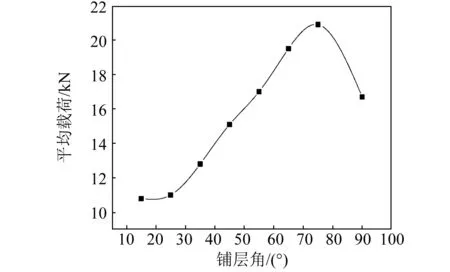
圖10 不同纖維鋪層角度對平均載荷的影響Fig.10 Effect of different ply orientations on Fmean

根據載荷效率的計算公式，如果平均壓潰載荷(Fmean)與峰值載荷(Fmax)越接近，即載荷-位移曲線與坐標軸圍成的區域越接近矩形，則載荷效率越接近100%，這是理論上最大的能量吸收效率。圖11給出了不同纖維鋪層角度對載荷效率的影響曲線，可見，±45°鋪層的載荷效率最高，約為60%。另外，從圖7計算偏軸剛度可發現鋪層角度在45°附近時Ex、Ey交叉，此時試件在軸向與周向的剛度非常接近，在壓潰過程中，達到峰值載荷之后，進入漸進破壞過程，峰值下降較少，因而載荷效率最高。

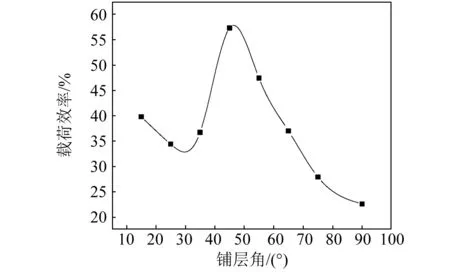
圖11 不同纖維鋪層角度對載荷效率的影響Fig.11 Effect of different ply orientations on LE

4 結 論

(1)通過將兩次重復試驗的結果進行對比分析，兩次試驗的峰值載荷偏差為9.14%，平均載荷的偏差為7.71%，比吸能的偏差為2.5%，表明此次試驗的重復性較好。然后，采用chang-chang失效準則，建立單層殼有限元模型，將仿真計算結果與試驗結果進行對比分析，仿真結果與試驗的峰值載荷偏差為7.18%，平均載荷偏差為2.14%，比吸能偏差為-4.06%，載荷效率偏差為-4.71%。表明仿真與試驗的載荷-位移曲線吻合度較好，從而驗證了本建模方法及復合材料薄壁圓管仿真模型。

(2)基于驗證的有限元模型，改變纖維鋪層角度，建立[±15°]6、[±25°]6、[±35°]6、[±45°]6、[±55°]6、[±65°]6、[±75°]6、[±90°]6復合材料薄壁圓管有限元模型，結果表明：在準靜態軸向壓潰作用下，隨著纖維鋪層角度的增大，薄壁圓管比吸能先增大，在75°之后減小。纖維角度為±45°時，初始峰值載荷最低，載荷效率最高，圓管更容易進入漸進破壞吸能階段。研究結果可為復合材料纖維鋪層角度設計及復合材料薄壁結構有限元建模提供參考。