生活中的數學

阮征 韓翔

【內容摘要】當前，在學生眼中，數學僅僅是作為考試及格的必考科目，學習數學僅僅出于應付考試，而畢業之后則嫌其無用，很快便遺忘掉了。其實數學是和現實生活息息相關的，生活中的很多問題都可以通過建立相應的數學模型來解決。本文就以生活中的未解之謎——百慕大三角為例，探究由其衍生出的數學習題，并拓展延伸出魔鬼三角問題的揭秘。

【關鍵詞】數學 生活 百慕大三角 衍生 揭秘

一、百慕大魔鬼三角的背景

在很多科學欄目中，都會經常提到一個地方：位于地球北緯30°的地方，有一個驚嘆全世界的地帶——著名的百慕大三角，它誕生四大文明古國，有許多奇妙的自然景觀，也留下了很多科學難解的，神秘、怪異、迷幻、恐怖……這里也一直存在著困擾科學家的未解之謎，因為神秘、事故頻發，而又不為人所知。世界歷史上最早經歷過的百慕大三角的人就是著名的航海家哥倫布。自那個時候開始，就開始流傳關于百慕大三角的詭異流言，相傳近百年的時間里，百慕大三角屢屢發生的海難、空難事件神秘莫測，震驚世界，又稱之為“魔鬼三角”，無數的飛機和船只在這里離奇消失、不見蹤跡。

近百年來有很多對于百慕大三角海域為何會出現如此眾多怪異之事的解釋，如時空隧道、海底裂縫、黑洞等學說，但都不夠嚴謹，經不起推敲。但百慕大三角的科學秘密并不是本文的研究重心，在這里筆者將重點探討百慕大魔鬼三角中衍生出的數學習題。

二、百慕大三角衍生出的數學習題

1.邏輯推理題

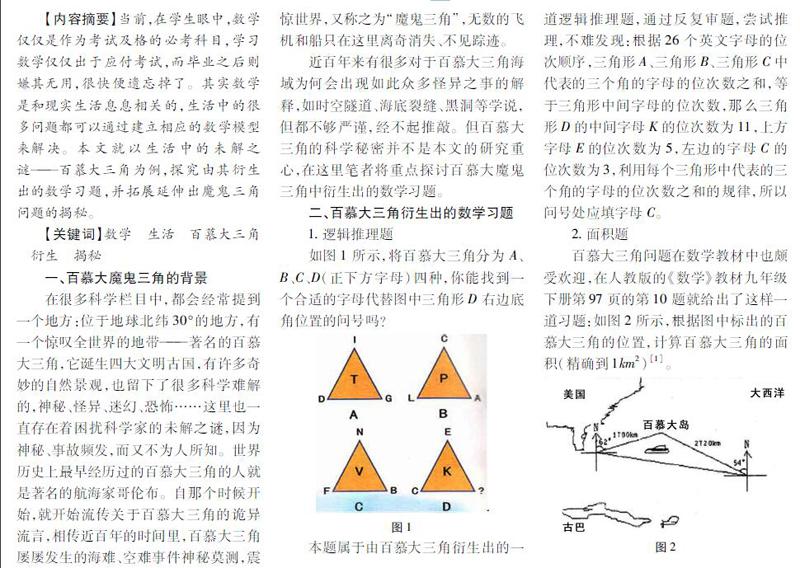
如圖1所示，將百慕大三角分為A、B、C、D（正下方字母）四種，你能找到一個合適的字母代替圖中三角形D右邊底角位置的問號嗎？

本題屬于由百慕大三角衍生出的一道邏輯推理題，通過反復審題，嘗試推理，不難發現：根據26個英文字母的位次順序，三角形A、三角形B、三角形C中代表的三個角的字母的位次數之和，等于三角形中間字母的位次數，那么三角形D的中間字母K的位次數為11，上方字母E的位次數為5，左邊的字母C的位次數為3，利用每個三角形中代表的三個角的字母的位次數之和的規律，所以問號處應填字母C。

2.面積題

百慕大三角問題在數學教材中也頗受歡迎，在人教版的《數學》教材九年級下冊第97頁的第10題就給出了這樣一道習題：如圖2所示，根據圖中標出的百慕大三角的位置，計算百慕大三角的面積（精確到1km2）[1]。

本題可采用割補法——百慕大三角的面積可以等于一個梯形的面積減去兩個三角形的面積構造出一個包含已知△ABC的梯形EFCA（如圖3所示），則S△ABC=S梯形EFCA-S△ABE-S△BFC，因而需要求出圖中五條線段AE、CF、BE、BF、EF的長度，解題所需的條件較多，求解的過程較為復雜[2]。那么有沒有簡便一點的方法呢？

其實這道題若不采用割補法，按照思維定勢，求三角形面積直接使用面積公式S=12×底×高，則只需求出已知邊上的高，未知量只有一個，解題過程將變得十分簡單：

解：如圖4，過點B作BD⊥AC，交CA的延長線于點D.

根據題意，得∠BAC=62°+54°=116°.

則∠DAB=180°-∠BAC=180°-116°=64°.

在RT△BAD中，sin∠DAB=BDAB.

那么BD=ABsin∠DAB=1700sin64°.

所以S△ABC=12AC+BD

=12×2720×1700×sin64°

≈2127100（km）2

答：百慕大三角的面積約為2127100km2.

3.內角題

泰勒斯想測量從百慕大海岸到海上的船只之間的距離，我們考慮一下在這種場合中的其他幾個問題：從船上看見百慕大海岸上的燈塔和大樹時，可以說只構成了一個角度，實際上如果走到船上無疑是會明白的，然而可以說在海岸上就能把它算出來，是怎么回事呢？

其實解決這個問題，利用下面這個定理再合適不過了——三角形的內角和為兩個直角的度數之和。

這樣一來，根據題意，要想求出圖5中∠BAC的度數，只有測出∠B和∠C，即可算出∠BAC =180°∠BAC =180-∠B -∠C.此時過點A做BC平行線XY，將∠B和∠C移到點A處，

則 ：∠B=∠XAB

∠C=∠YAC

+∠BAC=∠BAC

可得： ∠BAC+∠B+∠C=∠BAC+∠XAB+∠BYAC=180°.

本題使用了典型的分析-綜合的方法，由此還可衍生出從三角形的內角求出多邊形的內角：首先將n邊形分割成 個三角形，求出n個三角形內角的和，也就是兩個直角，如果將它們加起來，則為2n個直角，但由于中心點的周角為四個直角，因此n邊形的內角為（2n-4）個直角。

由此再補充一個與此不同的其他方法：有一個n邊形的道路，一輛汽車繞此道路跑一周，此時回到起始的位置，由于只轉了一圈，所以它方向的改變總計是四個直角。對三角形來說是四個直角，對百邊形、千邊形來說也是四個直角，只是方向的改變是一點一點進行的，這個值是恒定不變的。因此定理——“多邊形外角的和為四個直角” 成立。由此定理可得出下面的內角定理：在n邊形的一個頂點處，由于其內角與外角的和為兩個直角，其全部n個頂角就有2n個直角，所以，減去外角的和，即四個直角，則內角的和即為（2n-4）個直角。

三、啟示

通過前文對百慕大三角衍生出的邏輯推理題、面積題、內角題的探究，可以發現數學和我們的生活如影隨形，一個魔鬼三角問題可以衍生出一系列類型如此豐富的數學習題，由此不難看出，數學脫離不了生活，生活也脫離不了數學，不用說自然科學或技術方面離不開數學，即使在經濟、政治方面也離不開數學，相信關于百慕大魔鬼三角問題能夠衍生出更多的題目留給人們探究。

四、拓展——揭秘魔鬼三角之謎

關于魔鬼三角之謎的探究，國外有位研究漩渦的學者將一種強光以60°-75°的入射角，入射進模擬的旋渦中，結果這個“凹面鏡”聚焦點燃了一張薄紙片，這個實驗引起了他莫大的興趣。他斷言：百慕大三角區的百年懸案，有望就此真相大白。

原來百慕大三角區自五十年代以來，先后有上百架飛機、二百多艘艦船在這一片海域消失，就連氣象衛星也沒有找到真憑實據，但是從該區域的照片上可以清晰地反映出整個海區遍布著一個又一個巨大的漩渦，有的直徑數千米，有的甚至達數百公里。

所以，這位學者根據這次試驗的獲得的結果，給出了這樣的斷言：百慕大三角海區許許多多的巨大漩渦，就是無數個巨大的“凹面鏡”。每當太陽光的入射角在60°-75°范圍內時，照射在一個直徑1km的漩渦中，則聚光焦點的直徑就有1m左右，溫度可達幾萬度。這么高的溫度足可以使飛機、船艦頃刻間熔化或爆炸，而且漩渦的直徑越大，其聚光焦點的溫度也就越高。夜晚，沒有太陽光，漩渦雖然無法聚光，但由于巨大漩渦的旋轉速度極快，必然引起電磁場擾動，進而引起磁羅盤和其他的航海儀表失常，使飛機、船艦失控而葬身海底。這就是百慕大三角區經常飛機、輪船失事的原因的揭秘，加上本文對于百慕大三角衍生出的數學習題的解析，相信大家對于數學與生活的密切聯系有了更深層次的理解。

【參考文獻】

[1]魏祖成.對“百慕大三角問題”的疑惑[J].中小學數學（初中版），2010（10）：37.

[2]孔德艷.解題應從“簡”[J].中小學數學（初中版），2008（11）：35

作者簡介：阮征（1992-），女，漢族， 安徽合肥人，教育碩士研究生，碩士，主要研究方向：數學教育、數學課堂教學.

韓翔（1994-），男，漢族， 安徽淮南人，教育碩士研究生，碩士，主要研究方向：數學教育.

（作者單位：合肥師范學院 數學與統計學院）