一種高效的齒輪齒面偏差在機測量方法研究

周雯超，朱曉春，丁文政，孫曉敏

（南京工程學院 江蘇省先進數控技術重點實驗室，南京 211167）

0 引言

齒輪測量是確保齒輪質量和精度的關鍵步驟[1]，在傳統的齒輪制造過程中，齒輪的誤差測量是通過獨立的齒輪測量儀器來完成的[2]，這種工藝過程增加了齒輪制造過程的成本和制造周期，另外對于高精度和大尺寸的齒輪，離線測量會給高精度齒輪的二次裝夾以及大齒輪的搬運過程帶來很大麻煩。因此，充分利用數控磨齒機床工已有的數控軸，開發在機測量功能，構成一個具有加工和測量功能的齒輪制造的閉環系統，能大大提高齒輪加工質量和效率。近年來，研究學者對齒輪在機測量進行了大量研究。高峰[3]利用數控磨齒機的回轉軸（C軸）以及徑向進軸（X軸）給運動形成的理論漸開線建立了數學模型，進行了齒輪誤差的在機測量，而對于測量區域的選取、測量點數無明確規定。王志永[4]提出了一種針對螺旋錐齒輪的展成法在機測量方法，對理論齒面離散化，在齒長方向上取9列，齒高方向上取5行共45個離散點，但沒有明確說明測量點數的選取依據。楊靈敏[5]選取6組不同的測量點數對齒面誤差進行了在機測量，在保證精度和效率的情況下得出最佳點數，但沒有具體分析如何數確定測量點的數量。黃騰蛟[6]采用等徑向長度采樣法，選取了10個測量點，但沒有給出測量間距確定的依據。

在機測量，不僅要求所測的數據點能反應被測對象的誤差信息，同時還應提高在機測量的效率。本文針對齒輪齒面偏差的在機測量，在保證測量精度的前提下，提出了一種高效的在機測量方法。通過建立齒輪齒面的測量模型，對測量點進行了優化。優化重點聚焦于測量區域的確定、基于法曲率半徑的測量點數量規劃以及Hammersley序列的測量點分布規劃。

1 齒輪齒面的測量模型

以直齒輪為例，它的齒面是一個空間曲面，因在建立齒輪齒面的數學模型時選用曲面的參數方程。

1.1 漸開線齒廓上點K的方程

如圖1所示，在漸開線齒廓的軌跡上，rb為基圓半徑，A點為漸開線起點，漸開線齒廓上的一點為K，BK為基圓的切線，ξ為展開角，θ為漸開線齒廓的起點角度,則點K的方程為：

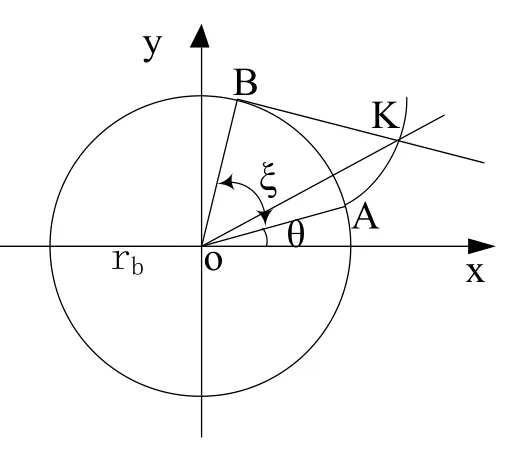
圖1 漸開線齒廓軌跡

點K的y軸坐標為：

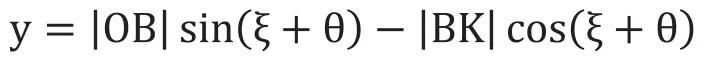
又因為：

故：

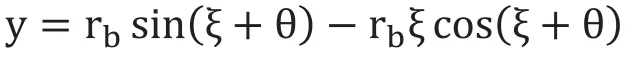
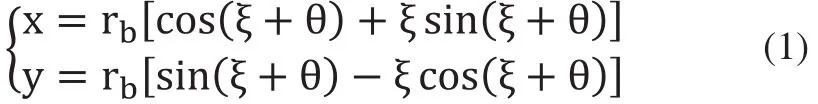
1.2 齒輪齒面上點K的方程

如圖2所示，直齒輪端面的圓心與測量坐標系原點O重合，且其中心軸重合于測量坐標系的z軸。直齒輪端面與xoy平面重合，其漸開線的起點為A0，與x軸所形成的夾角記作θ。取齒廓上一點記為K，設點K在齒面上的空間坐標為（x,y,z），ξ為點K的展開角，以逆時針方向的角度為正向角。平行于xoy平面取一個漸開線齒廓，其齒廓起點為A1，A1在xoy平面上的投影與A0重合。

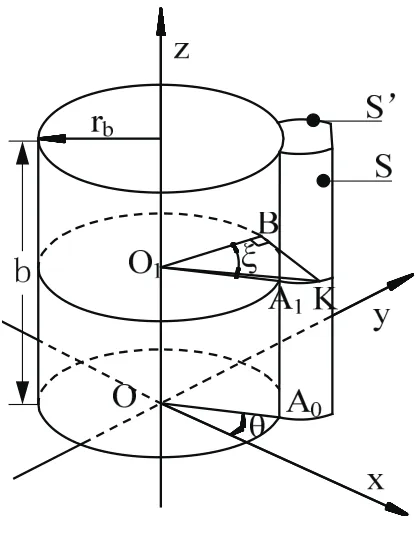
圖2 齒輪坐標系建立

假設齒輪的齒寬為b，在式(1)的基礎上，則點K的z軸坐標為：z=bi,bi∈[0,b]，可得齒輪齒面S上點K的坐標計算方法為：

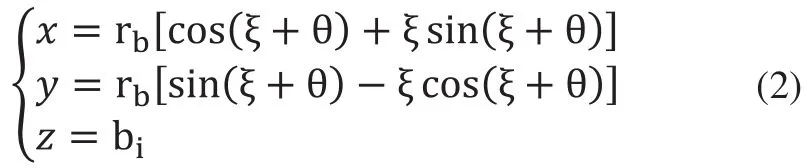
同理可得，假如點K在齒面S′上時，點K的坐標計算方法為：

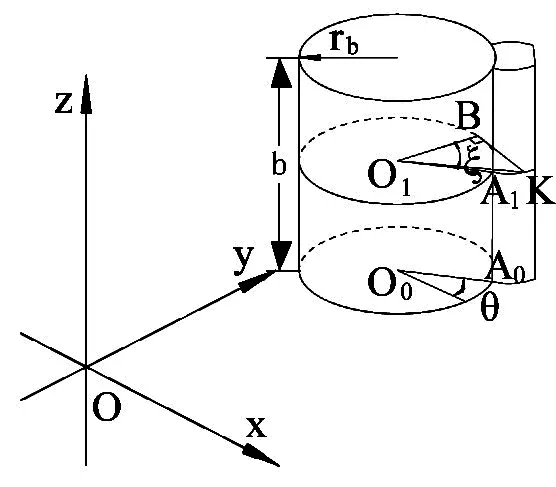
圖3 通常情況下的齒輪坐標系建立

如圖3所示，通常情況下，當直齒輪端面的圓心O0不與測量坐標系的原點O重合時，設O0的坐標為(x0, y0,z0)，由式(2)、式(3)可得點K的方程為：

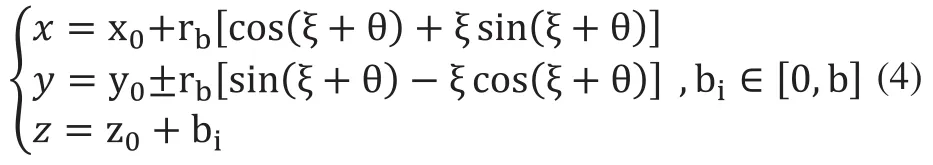
式中，當第一個輪齒的齒廓起點角度為θ0，則第j個輪齒的齒廓起點角為[7]：

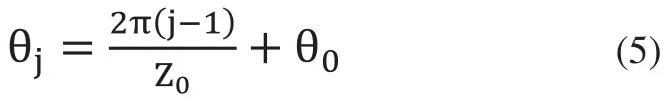
式中，Z0為齒輪的齒數，通過式(4)、式(5)，能夠得到輪齒j的所有齒面坐標。

2 齒面測量點優化

2.1 確定測量區域

手工劃定測量區域容易受人為因素的影響，無法保證測量點選取的科學性以及測量效率的提升。采取測量點的選取之前要先確定測量區域。如圖4所示，通常情況下，一個完整的齒輪齒面由齒頂部分，工作部分，過渡部分和齒底部分組成。

圖4 齒輪齒面的組成

其中工作部分起嚙合作用，因此本文將包含工作部分的四條邊界作為齒輪齒面偏差的測量區域。

2.2 測量點數量規劃

確定合理的測量點數量是提高在機測量效率的關鍵一步。曲率能決定測量點的集中程度，而齒面上某一方向的彎曲程度可由法曲率表示，那么法曲率越大的區域點數越集中，反之法曲率越小的區域點數越稀疏。因此，測量點數量規劃選用法曲率作為規劃依據，盡量減少測量點的數量，從而提高在齒輪齒面偏差在機測量的效率。

首先由齒面的參數方程，可表示為γ(θ,ξ)，對θ和ξ各自求導，得：

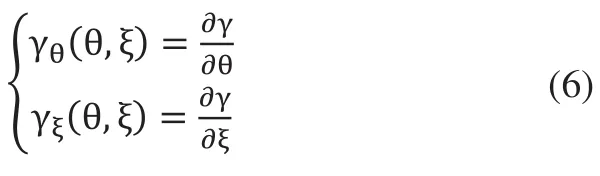
由曲面的第一基本齊式，可得：

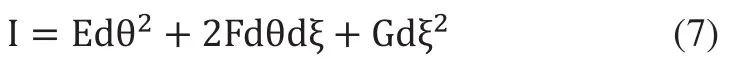
式中，系數E、F、G計算公式分別為：

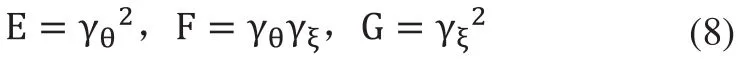
由曲面的第二基本齊式，可得：

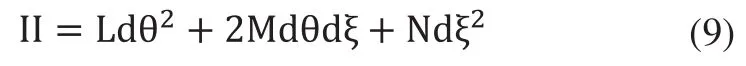
式中，系數L、M、N計算公式分別為：

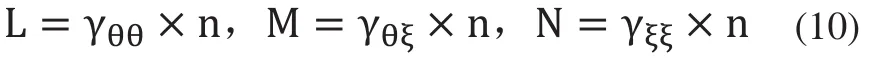
則齒面上測量點的法曲率kn可表示為：

對法曲率kn求導，可得：

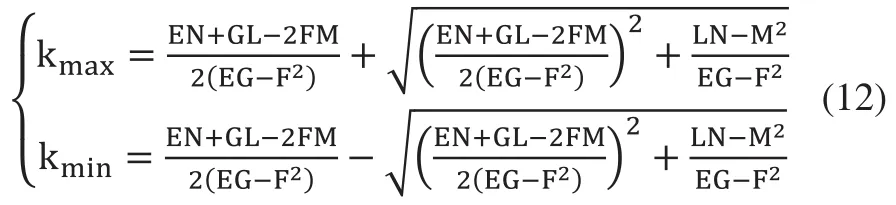
極小值kmin為法曲率kn的有效值，計算出測量區域上測量點的最大法曲率knmax，根據最大法曲率knmax求出對應的最小法曲率半徑rkmin。根據采樣定理f≥2fm（f為連續信號的采樣頻率，fm為連續信號的最高采樣頻率[8]）,故將最小曲率半徑rkmin的一半定為測量間距，即測量間距?l0的值為。在實際操作中，為了避免混頻現象的發生，至少需采4個周期[9]，因此測量間距?l的值為：

用測量間距?l對測量區域對應的漸開線弧長L進行等間距劃分，漸開線弧長L′：

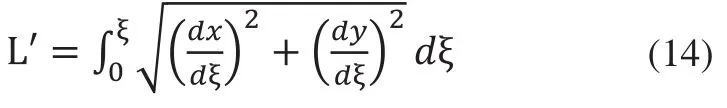
根據式(13)、式(14)可得測量點數量Q為：

2.3 測量點分布規劃

測量點的分布規劃方法有以下幾類：均勻分布法、隨機分布法及智能分布法等。這里采用隨機分布法中的Hammersley序列進行測量點的分布規劃。Hammersley序列的測量點的分布規劃是將齒輪齒面投影XOY平面上，進行測量點的分布規劃，將得到的二維點坐標轉化為三維點坐標，在解決齒面偏差的測量點分布上具有很好的效果，并且需要的測量點數較少，能顯著地提升在機測量效率。

由式(15)計算測量點數Q，二維Hammersley坐標點Ni(xi, zi)坐標的方程為[10]：

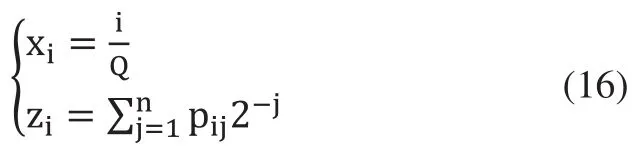
式中：xi≥0，zi≤1，i∈{1，…，m}，n為大于或等于log2m的最小整數，pi為測量點i的二進制編碼，pij是pi的第j個元素。

假設測量點數量Q為10，則可得Hammersley測量點分布如圖5所示。

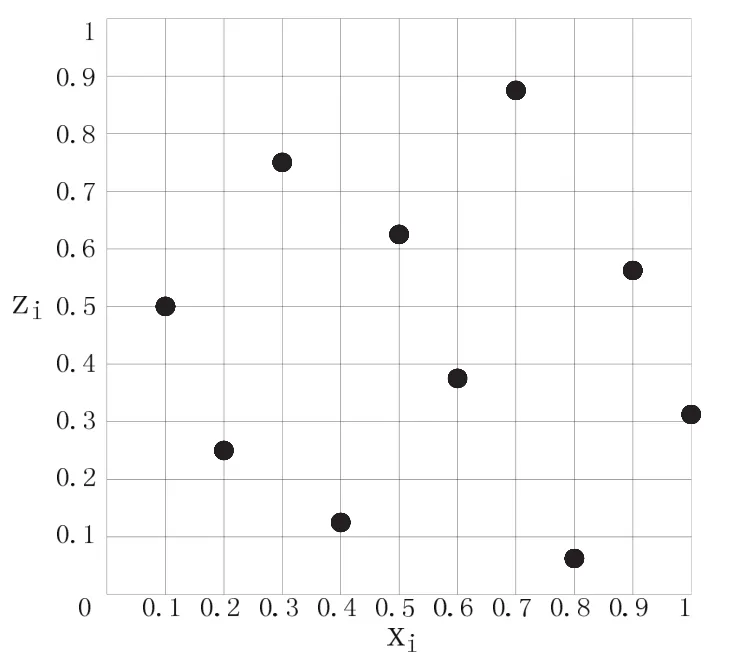
圖5 Hammersley測量點分布

將圖6中測量點的二維分布轉化為齒面上的三維分布，則可得到如圖7所示的齒面上的測量點分布圖。

3 齒面偏差計算

齒面偏差是指在端平面內，實際齒面偏離設計齒面的量，該量的計值方向是過實際加工齒面S*到設計齒面S的法線距離。對于理論設計齒面上一點K0，過其法線方向，找到與點K0對應的實際齒面S*上的點K*。計算該兩點之間偏差即為齒面加工時在K0點所形成的齒面偏差δ，即：

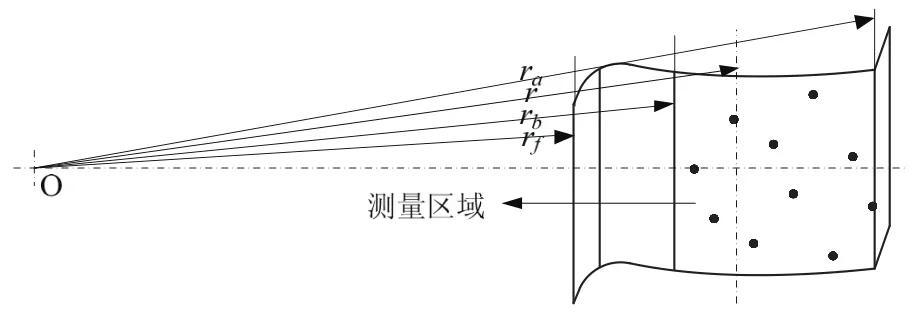
圖6 測量點分布圖

如圖7所示，K0K*是齒面偏差δ的幾何描述。

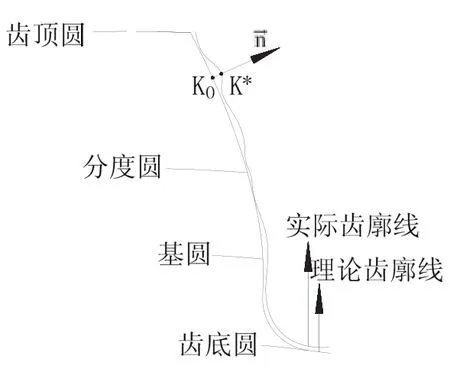
圖7 齒面偏差計算原理

4 在機測量實驗環境與結果分析

4.1 在機測量實驗環境

為了驗證測量點規劃的可行性，本文基于數控磨齒機現有結構的基礎上，增加雷尼紹測頭系統實現在機測量，搭建了齒輪在機測量試驗臺，主體主要由以下部分組成，如圖8所示。西門子SINUMERIK 828D數控系統、TK13200E系列數控轉臺、THK KR30系列三坐標滑臺裝置以及雷尼紹OMP60測頭系統。

圖8 在機測量試驗臺

在機測量的過程中，測頭球心的位置相對于待測齒輪的位置會不斷的改變，而齒輪在機測量的誤差數據處理是在待測齒輪工件坐標系中的，為了得到測頭的球心坐標變換到被測齒輪工件坐標系中，得到測頭球心相對于被測齒輪的實際位置坐標，需要建立在機測量坐標系。圖9中，待測齒輪工件坐標系的原點為O，測量坐標系的原點為Oc。

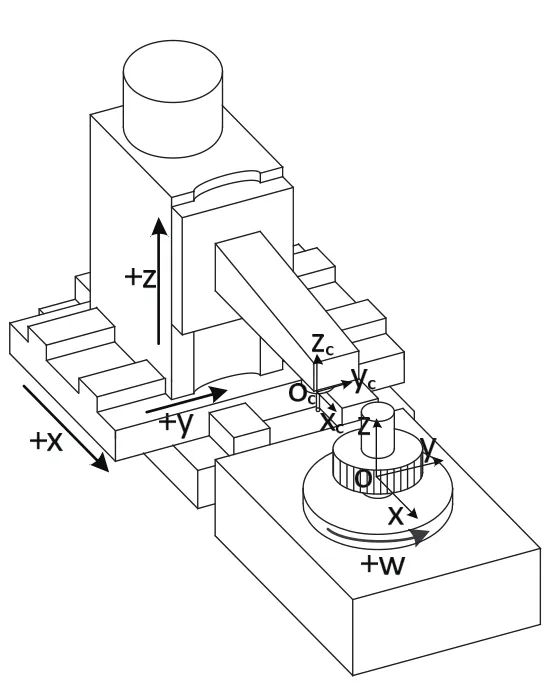
圖9 在機測量試驗臺坐標系建立

具體的測量過程如下：首先SINUMERIK828D數控系統根據接收到的測頭檢測程序，啟動雷尼紹OMP60測頭。先標定測頭，對齒輪工件校正，然后利用數控系統控制回轉工作臺慢慢旋轉，按照提出的齒面偏差測量點優化方案控制測頭進行測量，當測頭觸碰到齒輪齒面后，測頭控制器會反饋一個信號給數控系統，當數控系統接收到該信號后，將采集到的測量值和各坐標軸光柵的計數值存儲，然后進行下一個位置的測量，直到測量任務的完成。最后系統對所存儲的數據進行分析、處理，生成測量數據文件。如圖10所示為實際的齒面在機測量實驗圖。

圖10 在機測量實驗圖

4.2 結果分析

本文選定齒輪參數為模數m=4.5，齒數z=24，

分度圓直徑d=108mm，壓力角α=20°，齒頂圓直徑da=117mm，齒根圓直徑df=96.75mm，基圓半徑rb=50.74mm，齒寬b=20mm的標準齒輪作為在機測量對象。此時，對齒廓起點角度θ=0°的齒面（記為1號齒面）進行建模，此時可計算出展開角ξ∈[0°，32.877°]，根據式(4)可得：

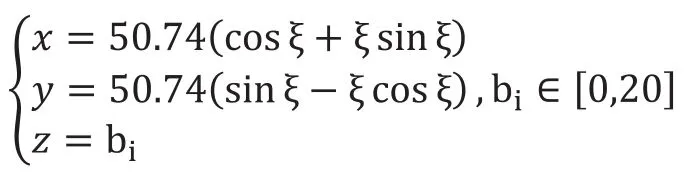
根據式(12)可得最大的法曲率為knmax≈0.12453，則法曲率半徑

根據式(16)計算出如圖12所示的實驗測量點分布。

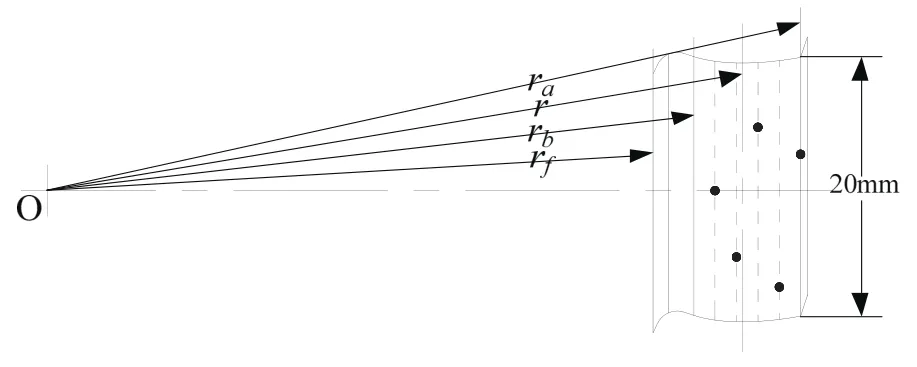
圖11 實驗測量點分布

根據給定的齒輪參數按照所提出的測量點優化方案選取測量點進行在機測量，將測得的數據根據式(17)分別計算出每個測量點處的齒面偏差δ，如表1所示。

表1 齒面偏差在機測量值

由表1測量數據可知，δmax=21.9um、δmin=14.8um。

在JD45齒輪測量儀對1號齒面進行測量，得到的最大齒面偏差為：δmax=19.8um，最小齒面偏差測δmin=15.3um，測量精度符合測量要求。

表2 隨機均勻采點的測量數據

接下來，在齒輪在機測量試驗臺上對1號齒面隨機均勻采點16個，得出的數據如表2所示。

由表2測量數據可知，δmax=20.4um、δmin=14.9um。

與傳統的測量方法以及在齒輪在機測量試驗臺上測量點隨機采點比較，本文測量點的優化方案減小了測量區域，同時壓縮了測量點數量，在保證測量精度的同時提高了測量效率，驗證了本文的在機測量方法是有效、可行的。

5 結束語

為了實現齒輪齒面偏差在機測量過程中的快速測量，本文重點研究了齒面的測量點優化。通過建立齒輪齒面的測量模型，在齒面的區域上規劃了滿足精度要求的測量點數量和分布方案。實驗結果驗證了該方法是有效的。因此，文中提出的方法可為齒輪在實際生產中齒面偏差的在機測量提供借鑒，有效地提高測量效率，節約了制造時間和成本。