雙SCARA機器人運動學及奇異性分析

申浩宇，劉艷梨，吳洪濤

（1.陜西國防工業職業技術學院 機電工程學院，西安 710300；2.南京航空航天大學 機電學院，南京 210016）

0 引言

當前，機器人技術在很多領域都得到了廣泛的應用。其中，并聯機器人系統具備著特有的高精度，高剛度，高承載力，自重負荷小等多方面優點，自問世以來，就引起了極大的關注。近些年，有關并聯機器人的研究熱潮更是被不斷地掀起[1～3]。

伴隨著研究的深入，并聯機器人的構型越來越多。在種種并聯機器人的構型中，平面五桿機構的機械結構相對簡單，并且運動學分析難度較低。在一些特定的工業場合，例如涉及到大量微小零部件的裝配作業，平面五桿機構便于控制，重復定位能力高，成本低等方面的優勢能夠被更為明顯的體現出來[4～8]。因此，以平面五桿機構為基本構型的并聯機器人的研究受到了越來越多研究人員的關注[9～11]。例如，由三菱電機公司開發的RP-AH系列“雙SCARA”機器人已經實現了產業化和商業化，由加拿大ETS學院開發的DexTAR機器人也非常適用于裝配金屬球等小零件的作業[12,13]。伴隨著技術的不斷完善和發展，該平面并聯機器人技術必然會被更為廣泛地應用在工業自動化生產領域中。

并聯機器人的奇異性分析是一個重要的研究內容，尤其在機器人的機構設計中占有非常重要的地位。當機器人處于奇異位形時，會減少或增加一個或多個自由度，機構的運動狀況會因此受到很大的影響。因此，奇異性分析在并聯機器人的研究中十分重要，可為機構設計及優化提供必要的依據。

本文在平面五桿機構的基礎上，提出了一種新型的雙SCARA機器人。針對該機器人，進行了運動學求解，得到了正向運動學的解析解, 進一步獲得了關節速度向量和末端速度向量之間的兩個雅可比矩陣。然后,在給定幾何參數的前提下，根據機器人雅可比矩陣的行列式對該平面并聯機器人進行了奇異性分析，利用關節變量得到了反映機器人奇異位形的奇異性曲面。

1 雙SCARA機器人結構

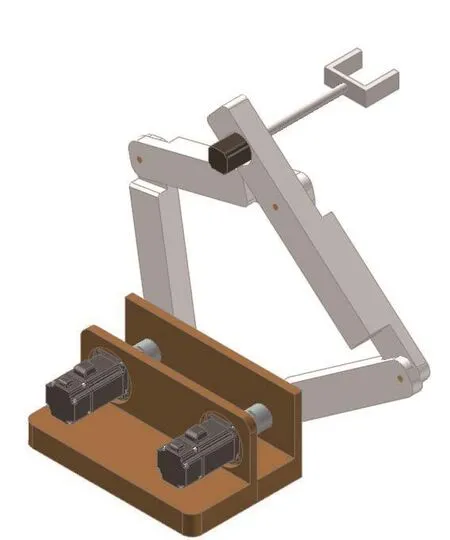
圖1 雙SCARA機器人的CAD模型

雙SCARA機器人的結構如圖1所示，由4個連桿及其支架，三個電機及末端手爪組成，連桿之間，連桿與支架之間均為旋轉副連接。該機器人有三個自由度，可以實現平面上沿著兩個坐標軸（X軸、Y軸）方向上的平動和繞著一個坐標軸（Z軸）的轉動。需要指出的是，X-Y平面內的平動是由該機器人機構中的平面五桿機構的運動來實現的，而末端抓手的轉動則是由軸3，通過安裝在連桿4上的一個電機來實現的。

2 正向運動學模型

在正向運動學問題中，即是給定機器人的關節變量，求解出機器人末端的位置和姿態。對于并聯機器人而言，通常情況下，正向運動學求解與反向運動學求解相比，難度更大。但是對于本文中提到的雙SCARA并聯機器人，由于其比較簡單的機械結構，正向運動學的求解可以通過解析的形式表達出來。

機器人的機構簡圖如圖2所示，Oi表示連桿在支架上的固定點，Li表示連桿i的長度，θi表示關節i的旋轉角度。機器人末端的位置和姿態由X=[XD，YD，α]來表示，關節變量由θ=[θ1，θ2，θ3]來表示。正向運動學求解問題，即是給定關節變量θi，求解X=[XD，YD，α]。

圖2 雙SCARA機器人的運動學簡圖

通過圖2，可以得到以下的推導內容。

機器人末端的位置D點的坐標為：

其中：

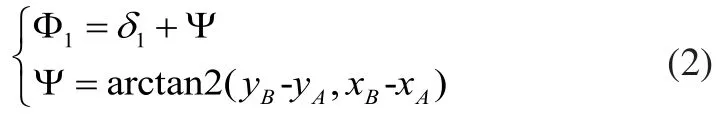
兩個關節點A和B的位置坐標可以通過關節變量θi表示為以下形式：

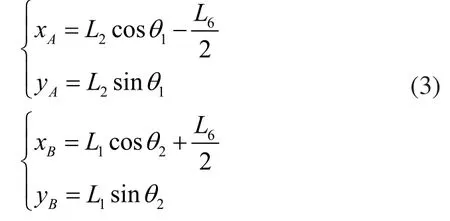
式(1)中，變量1δ由下式給定：

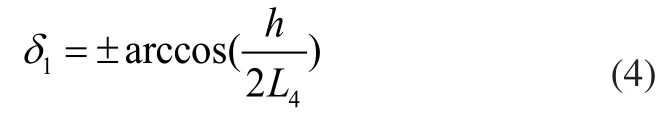
其中：

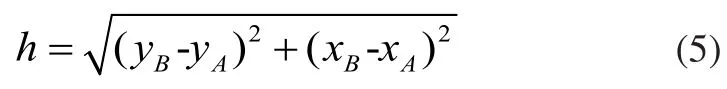
式(3)中的符號“±”表示機器人的兩種工作模式，從而該機器人擁有兩組正解，最后，機器人末端的姿態角α可以由下式給定：

此處：

式(1)和式(6)即為雙SCARA機器人的正向運動學方程。

3 基于雅克比矩陣的奇異性分析

根據Gosselin和Angeles提出的奇異性分析方法，由并聯機器人的運動學方程，該機器人的關節輸入向量和末端輸出向量之間存在著是一個非線性的運動學約束關系：

在本文案例中，上式是一個三維方程，式(8)對時間進行一階求導，即可得到輸入速度向量和輸出速度向量之間的關系：

此處，Jx和Jθ均是三維的雅克比矩陣。當矩陣Jx和Jθ的發生奇異時，機器人處于奇異位形。在對Jx和Jθ進行奇異性分析的基礎上，可以把并聯機器人的奇異位形分為三類：

第一類奇異：稱為逆運動學奇異, 顧名思義，即當det(Jθ)=0時的奇異性。此時Jθ奇異，并聯機構失去至少一個自由度。這種奇異位形發生在機構的工作空間邊界，也稱為邊界奇異。

第二類奇異：稱為正運動學奇異。即當det(Jx)=0的奇異性。此時Jx奇異，當所有的驅動關節無輸入時，并聯機構末端依然可產生微小運動。從而，并聯機構至少獲得了一個自由度。

第三類奇異：稱為綜合奇異。當Jx和Jθ行列式同時為零時的奇異性。此時，所有關節均無輸入時，末端還能產生微小運動；而當所有的關節均有輸入時，末端可以依然靜止。

4 雅克比矩陣的建立

將該雙SCARA機器人的正向運動學方程改為式(8)所示的形式：

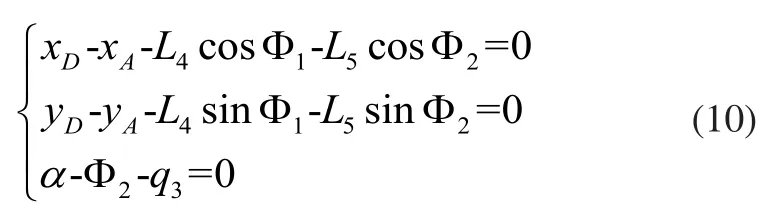
對式(10)進行一階求導，得到式(9)的形式：

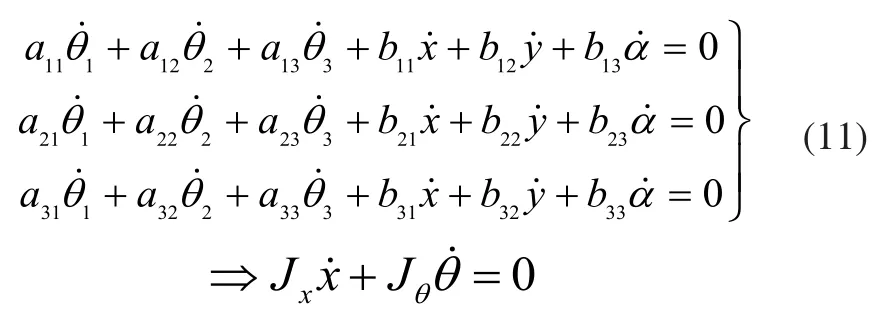
此處：

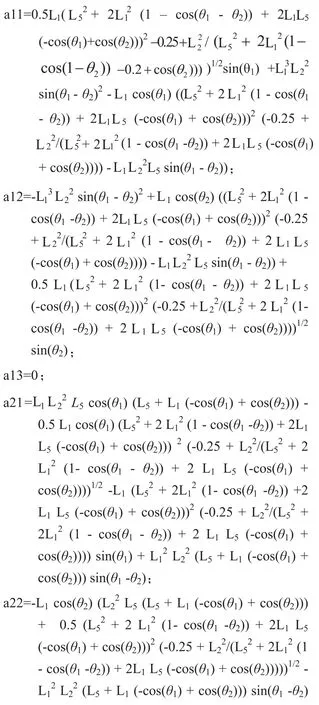
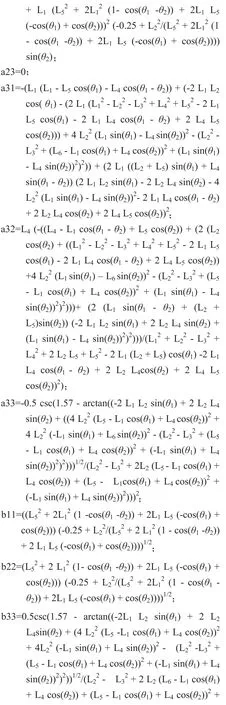
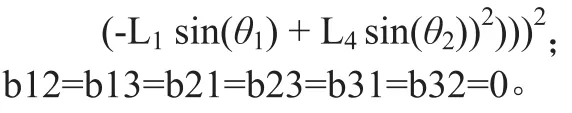
在給定機器人各個連桿的幾何參數的前提下通過雅克比矩陣Jθ和Jx行列式的值得表達式，即可得到使得雅克比矩陣行列式值為0的奇異位形曲面。

5 算例分析

取雙SCARA機器人結構參數：L1=L2=L3=L4=L5=1m，L6=1.5m。三個關節運動范圍均為：0≤θ1，θ2，θ3≤2π。在Mathematics 9.0的軟件環境下編寫了程序，對矩陣Jθ和矩陣Jx的行列式值為零的曲面進行了繪制，三個關節角使得矩陣Jθ的行列式值為零的變化曲面如圖3所示，三個關節角使得矩陣Jx的行列式值為零的變化曲面如圖4所示。

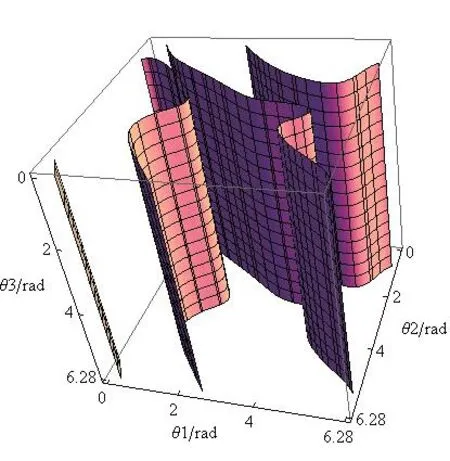
圖3 det(Jθ)為0時的三個關節角的變化曲面

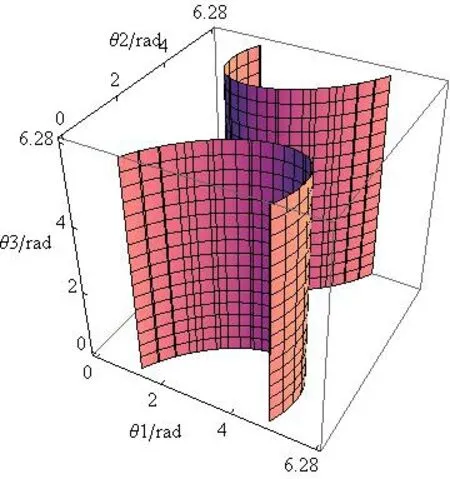
圖4 det(Jx)為0時的三個關節角的變化曲面

當關節角θ1，θ2，θ3的取值位于圖3所示曲面上時，det(Jθ)為0，雙SCARA機器人處于逆運動學奇異位形。當關節角θ1，θ2，θ3的取值位于圖3所示曲面上時，det(Jx)為0，雙SCARA機器人處于正運動學奇異位形。當三個關節角的取值位于圖3和圖4曲面的相交面上時，即det(Jθ)和det(Jx)同時為0，此時，機器人處于綜合奇異位形。

6 結論

針對提出的雙SCARA并聯機器人機構，進行了正向運動學建模及雅克比矩陣的建立。利用雅克比矩陣的行列式值，對其奇異位形進行了分類。最后，在給定結構參數的情況下，針對一個仿真案例，在Mathematic9.0中編制了奇異曲面繪制程序，繪制了該雙SCARA并聯機器人的奇異性曲面。通過該方法，可以在雙SCARA并聯機器人的設計過程中，及時對給定結構參數下的機器人奇異位形進行預測，從而為進一步實現機器人的軌跡規劃和工作空間優化提供了依據。