例談數列中的難度較大的綜合應用題
■廣東省興寧市第一中學 藍云波
數列是高考中的核心考點,在歷年的高考中都占有重要的地位。因此,如何高效學習好這部分內容變得至關重要。數列知識考點繁多,處理問題的思想方法較為靈活,問題的綜合程度較高,在高考中已經形成了很多經典問題。下面通過對高考中數列綜合應用問題的分析,可溝通數列的所有重要的知識與思想方法,同時也能體會到數列與其他重要知識點的精彩交匯,以期對同學們的學習有所幫助。
一、數列與數學文化的交匯
例1 《九章算術》“竹九節”問題:現有一根9節的竹子,自上而下各節的容積成等差數列,最上面4節的容積共3升,最下面3節的容積共4升,則第5節的容積為____升。
解析:設竹子從上到下的容積依次為a1,a2,…,a9,由題意可得a1+a2+a3+a4=3,a7+a8+a9=4。設等差數列{an}的公差為d,則有4a1+6d=3①,3a1+21d=4②。
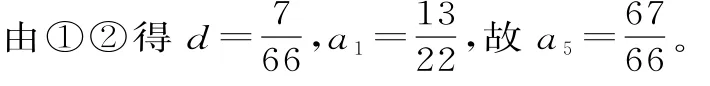
點評:此題是數學文化題,關鍵是提取其中的重要信息,可發現此題實際上是等差數列問題。
二、an與Sn的關系問題
例2 設數列an{}的前n項和為Sn,已知an>1,a2n+3an=6Sn-2(n∈N*)。

由題意知:
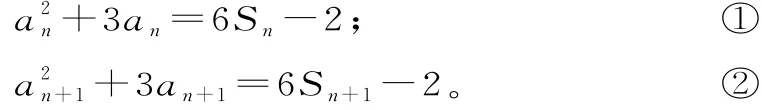
整理得(an+1+an)(an+1-an)=3(an+1+an)。因為an>1,所以an+1+an≠0,an+1-an=3。
所以數列{an}是以2為首項,以3為公差的等差數列。
因此,an=2+(n-1)×3=3n-1。
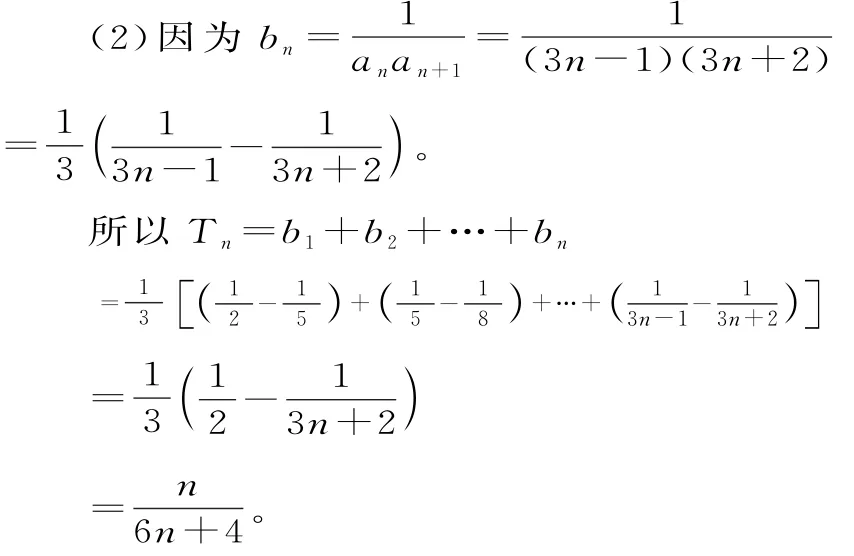
點評:對含有an與Sn的關系式的數列問題,可利用公式an=Sn-Sn-1(n≥2)實現問題的求解。
三、等差數列與等比數列的綜合問題


點評:本題綜合考查了等差數列與等比數列的基礎知識,解題的關鍵是對基本概念、公式的理解。
四、數列中的最值問題

解得6≤n≤7。
又n∈N*,所以最大項為第6項和第7項。
五、數列中的比較大小問題


當n≥3時,f(n+1)-f(n)>0,故當n≥3時,f(n)單調遞增。
因此,當n≥4時,f(n)≥f(4)=1。
而g(n)<1,所以當n≥4時,f(n)>g(n)。
經檢驗n=1,2,3時,f(n)>g(n)仍成立。
點評:比較大小是數列中的常見問題,常見的解法有:直接作差法,借助中間變量法,構造函數進而利用其單調性等方法。結合此題的特點,可借助中間變量進行比較。
六、數列中的恒成立問題

(2)若對任意的n∈N*,不等式3n2-2n-5<(2-λ)an恒成立,求實數λ的取值范圍。


點評:含有參數的恒成立問題,分離參數是常見的解題策略,本題在分離參數后,通過借助數列的單調性求出數列的最大項,從而實現問題的求解。
七、數列中的不等式證明問題
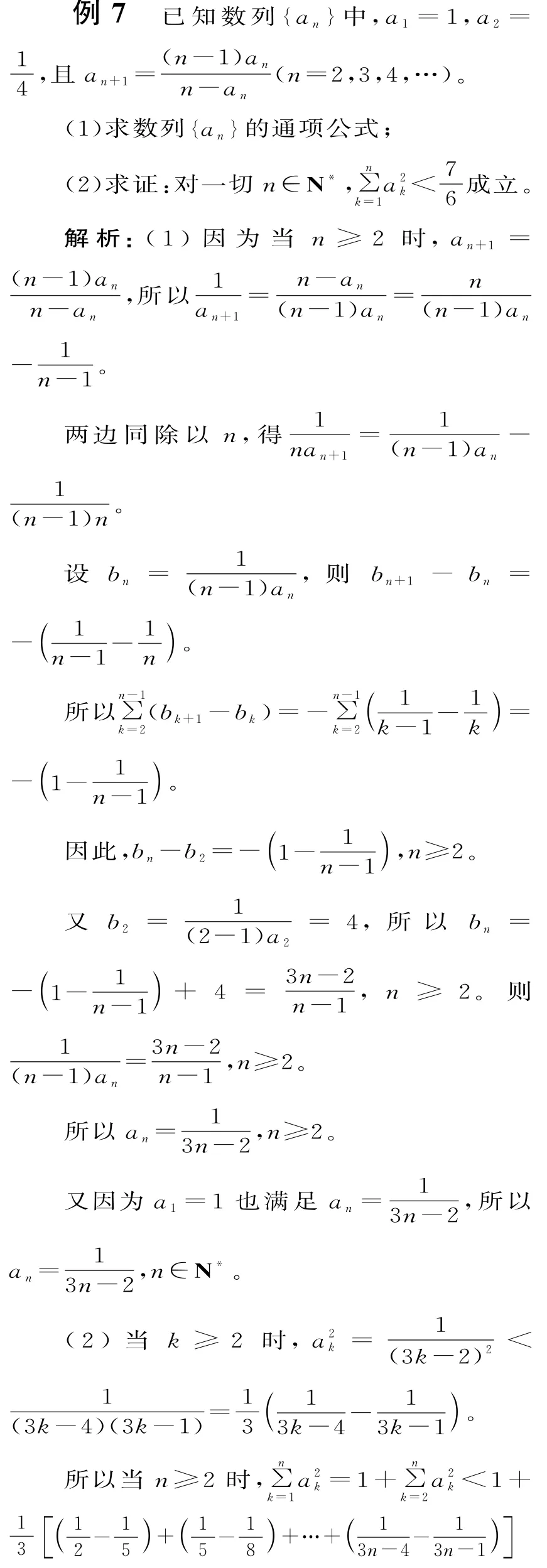
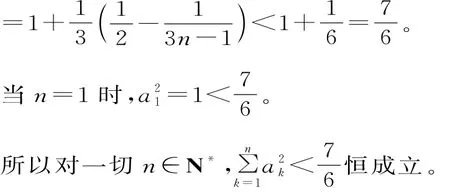
點評:本題的關鍵是通過倒數變換,然后通過拆項,再利用累加法實現問題的求解。對代數變形能力要求較高,較為隱蔽,在證明不等式的過程中使用了常見的放縮法。
八、函數背景下的數列問題

點評:這是一道極為經典的倒序求和問題,這類試題往往給出一個優美的函數,然后借助該函數蘊含的一個奇妙性質進行求和,而這個蘊含的奇妙性質,往往需要對所需求和的式子進行觀察而獲得。
九、解析幾何背景下的數列問題
例9 設C1、C2、…、Cn、…是坐標平面上的一列圓,它們的圓心都在x軸的正半軸數n,圓Cn都與圓Cn+1相互外切,以rn表示Cn的半徑,并且{rn}為遞增數列。
(1)證明:{rn}是等比數列;

而λn+1=λn+rn+rn+1=2rn+1,將λn=2rn代入,解得rn+1=3rn。
故{rn}是公比q=3的等比數列。
(2)由于r1=1,q=3,故rn=3n-1。
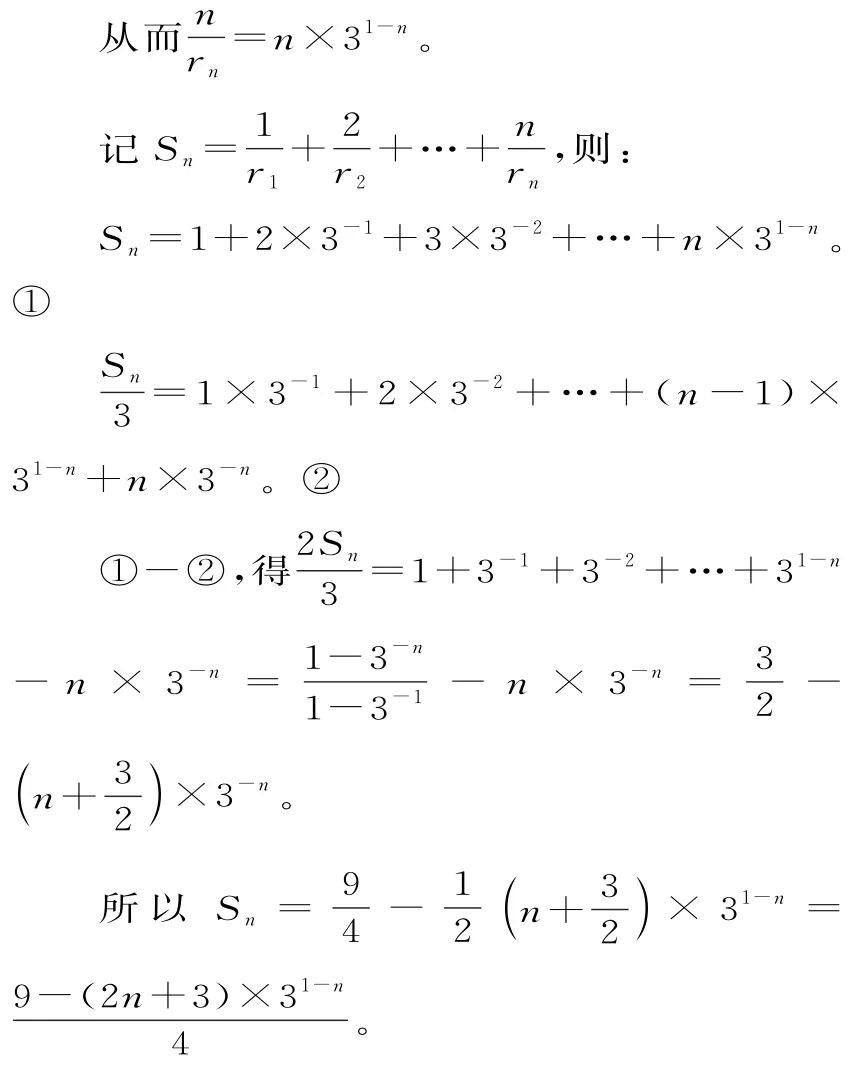
點評:本題以解析幾何為背景,通過數形結合,轉化為數列問題,第二問考查了錯位相減求和法。
十、平面向量背景下的數列問題
例10 設x軸、y軸正方向上的單位向量分別是i、j,坐標平面上點An、Bn(n∈
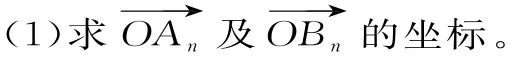
(2)若四邊形AnBnBn+1An+1的面積是an,求an(n∈N*)的表達式。
(3)對于(2)中的an,是否存在最小的自然數M,對一切n∈N*都有an<M成立?若存在,求出M;若不存在,說明理由。

因此,存在最小的自然數M=6,對一切n∈N*,都有an<M成立。
點評:本題通過向量的回路法,轉化為已知條件的向量進行表示,并通過平面向量的坐標運算解題。

