賞析數列中的創新題
■河南省潢川高級中學 謝思源
數列,作為高考的必考內容,除考查數列知識的基本應用外,同時也考查數列的創新問題,本文列舉幾例,供同學們欣賞。
一、新定義型
例1 設Sn為數列{an}的前n項和,(n∈N*)是非零常數,則稱該數列為“和等比數列”。若數列{cn}是首項為2,公差為d(d≠0)的等差數列,且數列{cn}是“和等比數列”,則d=_____

因為數列{cn}是“和等比數列”,所以為非零常數,d=4。
評注:所謂“和等比數列”,其實就是等比數列與等比數列求和的“綜合”,因此解決這類問題只需化“陌生”為“熟悉”,利用已經掌握的有關知識解決新問題。
二、圖表類型
例2 如圖1所示,將若干個點擺成三角形圖案,每條邊(包括兩個端點)有n(n>1,n∈N*)個點,相應圖案中總的點數記為=( )。
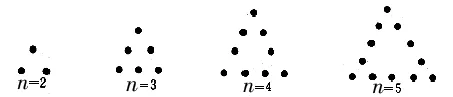
圖1


解析:由圖形可知a2=3=3×(2-1),a3=6=3×(3-1),a4=9=3×(4-1),a5=12=3×(5-1),…,an=3(n-1)。
故數列an是首項為3,公差為3的等差數列,通項為an=3(n-1)(n≥2)。

評注:本數列題以圖形的形式給出,既考查了考生的觀察能力和歸納能力,又考查了數列的基本考點:數列求和。題目的結構新穎,難度中等。
三、結論探索型
例3 若數列{an}滿足:存在正整數T,對于任意正整數n都有an+T=an成立,則稱數列{an}為周期數列,周期為T。已知數列{an}滿 足 a1=m(m>0),an+1=
①若a3=4,則m可以取3個不同的值;
②若m=2,則數列{an}是周期為3的數列;
③?T∈N*且T≥2,存在m>1,使{an}是周期為T的數列;
④?m∈Q且m≥2,使數列{an}是周期數列。
其中所有真命題的序號是____。
解析:對于①,根據條件,當m>2時,有a2=m-1>1,a3=m-2,于是m-2=4,有m=6滿足條件;當m∈(1,2]時,有a2=m-

對于②,逐個推導可得:a1=2,a2={an}是周期為3的周期數列。故②正確。
對于③,要想使得{an}是周期為T的周期數列,并且m>1,故只需使得a=,則TaT+1=m。而m>1,可使得aT=m-(T-1),即m-(T-1)=, 于是m2-(T-1)m-1=0,關于m的方程兩根之積為-1,必為異號兩根,而兩根之和為T-1≥1,故其正根m必定大于1,滿足條件,故③正確。
對于④,仿照③可知,當T=1時,m=1不滿足條件。
當T∈N*且T≥2時,若m為整數,則必定在若干項以后出現an=1,從這項以后成為常數數列,不合題意,故m為非整數,且舍負,要使得m∈Q,則 T2-2T+5必為有理數(且為整數)。令其為n,且T-1+n不是偶數,否則m為整數,即T+n是偶數,所以T與n同奇或同偶。由T2-2T+5=n2知,T與n不能同為偶數。當T為奇數時,T2是奇數,等式左邊是偶數,這與n2為奇數矛盾。
綜上,④錯誤。
所以正確答案為:①②③。
評注:本題給出周期數列的定義,又以遞推關系的形式給出了數列{an},要求大家從這兩個“已知”出發,探究給出的四個結論的真假性,試題具有較高的難度,從一定程度上考查了同學們的探究能力。
四、知識綜合型
例4 已知點A(1,0),B(0,1)和互不相同的點P1,P2,P3,…,Pn,…滿足(n∈N*),其中{an}、{bn}分別為等差數列、等比數列,O為坐標原點,若P1是線段AB的中點,則:
(1)求a1,b1的值。
(2)點P1,P2,P3,…,Pn,…能否在同一條直線上?請證明你的結論。

(an-an-1)(bn+1-bn)-(an+1-an)·(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?bn+1-bn=bn-bn-1?q=1,這與q≠1矛盾,所以當d≠0且q≠1時,P1,P2,P3,…,Pn,…不可能在同一條直線上。
評注:本題將等差數列、等比數列、平面向量和解析幾何交匯在一起,注意題中“平面向量”只是問題的“載體”,而“數列”才是問題的“落腳點”。

