隆低重心 提升素養
——談數列學習與問題求解

■浙江省杭州市余杭區教育局教研室 曹鳳山（特級教師）

數列是高中數學的主干知識,又是學習高等數學的基礎,高考對這部分內容每年都會重點考查,通常采取“一大一小”的模式,重在考查數列的概念、兩個基本數列、通性通法和重要的數學思想方法,有些問題與函數、不等式、解析幾何、三角函數等綜合,在知識交匯點上命制試題。由于數列內容上的獨特性,我們在解題與學習時要注意相應的方法。

一、關注基本量

例1 （2014年浙江高考數學試題）已知等差數列{an}的公差d＞0。設{an}的前n項和為Sn,a1=1,S2·S3=36。

（1）求d及Sn;

（2）求m,k（m,k∈N*）的值,使得am+am+1+am+2+…+am+k=65。

分析：本題以等差數列為背景,給出兩個獨立的條件,第一問求公差與前n項和,可以根據相應的公式求解,第二問,給出和求起始項與項數,一個方程兩個未知數,一般情況下不能求解,但是注意到m,k∈N*的條件,可以分析破解。

解：（1）由題意知（2a1+d）（3a1+3d）=36。

將a1=1代入上式解得d=2或d=-5。

因為d＞0,所以d=2。

從而an=2n-1,Sn=n2（n∈N*）。

（2）由（1）得am+am+1+am+2+…+am+k=（2m+k-1）（k+1）。

所以（2m+k-1）（k+1）=65。

由m,k∈N*知2m+k-1≥k+1＞1。

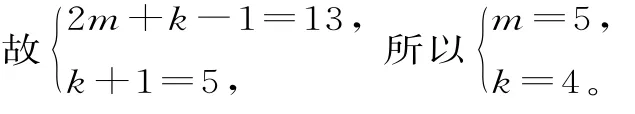
歸納：在一個（一類）數學問題中,可能涉及許多量,但其中有幾個量是獨立取值的,其他量則是這些量的函數,當我們選定任意一組這樣的量作基本量,那么問題就歸結為研究各基本量之間的關系。這種著眼于基本量解決問題的方法叫基本量法。在等差、等比數列中,已知五個元素a1,an,n,d（q）,Sn中的任意三個,便可求出其余兩個,即“知三求二”。其中確定基本量（a1,d（q））是典型方法,一個數列一旦能確定這兩個量,那么其他問題也就迎刃而解。

（2）在公比為正數的等比數列an中,已知a1+a2+…+an=2,an+1+an+2+…+a3n=12,則a3n+1+a3n+2+…+a6n的值是 。

分析：（1）本題以等差數列為背景,給出一個等式,基本量不能確定,需要改變角度,比如整體求解,利用數列的性質等。根據基本公式,等差數列單個項與前n項和沒有直接關系,兩項和才能建立聯系,可以考慮通過等差中項去轉化;另一個角度,問題并不是要求出項、求出和,而是已知和的比求項的比,兩者之間應該有量的關系,可以考慮整體求解。

歸納：利用方程求解基本量時,有時可能會出現未知數個數多于方程個數的情況,或者雖可求解但運算相當煩瑣,這時可以考慮用整體思想解決。整體思想即求與已知量（或可求量）的整體有關的量,表現為整體求解、整體代換、整體運算等多種形式。整體運算往往是數列某種性質的表現,對于數列的一些性質,能夠理解、運用最好,不能記憶、運用的也沒有問題,只要注意基本量和整體運算即可。

二、落實基本方法

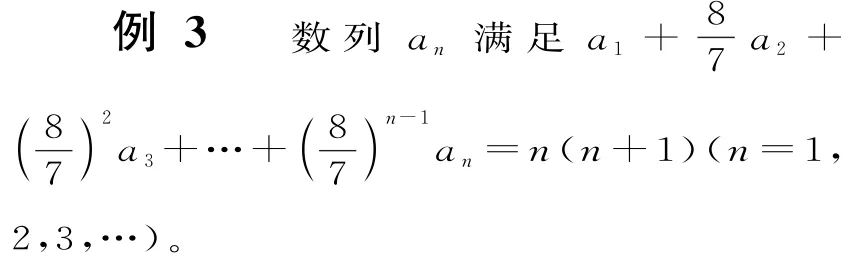
（1）求數列an的通項公式;

顯然,當n≤7時,an+1≥an?a1≤a2≤…≤a7≤a8;當n≥7時,an+1≤an?an+1≤an≤…≤a8≤a7。數列an先增后減,當n=7,

歸納：通項往往是數列問題的核心,求解通項的方法靈活多樣,如利用基本公式、整體求解、遞推、累加（積）、利用an與Sn的關系等。

數列與函數、方程、不等式等的綜合問題一般與函數的性質、方程的解等相聯系,數列作為特殊函數主要在于其定義域的限制,既要考慮處理函數性質的一般方法,也要考慮其“個性”,比如其單調性、最值問題等。

例4 （2018年浙江高考數學試題）已知等比數列{an}的公比q＞1,且a3+a4+a5=28,a4+2是a3,a5的等差中項。數列{bn}滿足b1=1,數列{（bn+1-bn）an}的前n項和為2n2+n。

（Ⅰ）求q的值;

（Ⅱ）求數列{bn}的通項公式。

分析：（Ⅰ）給出等比數列與兩個獨立的條件,運用等比數列的通項公式和等差數列中項性質,解方程可得公比q。

（Ⅱ）設cn=（bn+1-bn）an=（bn+1-bn）·2n-1,運用數列的遞推式可得cn=4n-1,再由數列的恒等式求得bn=b1+（b2-b1）+（b3-b2）+ … +（bn-bn-1）,運用錯位相減法,可得所求數列的通項公式。

解：（Ⅰ）等比數列{an}的公比q＞1,且a3+a4+a5=28,a4+2是a3,a5的等差中項,可得2a4+4=a3+a5=28-a4,解得a=8,由+8+8q=28,可得q=24,則q的值為2。

（Ⅱ）設cn=（bn+1-bn）an=（bn+1-bn）·2n-1,可得n=1時,c1=2+1=3。

n≥2時,可得cn=2n2+n-2（n-1）2-（n-1）=4n-1,上式對n=1也成立。

故（bn+1-bn）an=4n-1。

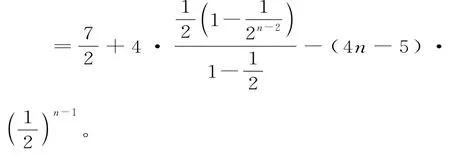
歸納：數列求和是數列的核心知識點之一。求和的方法非常靈活,如利用等差、等比數列的求和公式、分組求和、錯位求和、裂項抵消求和等。以上這些基本方法都有相對明確的使用條件和相對固定的步驟,我們要理解其使用條件,熟悉其步驟。

當然,通性通法也不是一成不變的,也要與時俱進,比如以上錯位相減求和就可以轉如反掌,而如何裂項呢?只需用待定系數法,大家不妨一試。

例5 正項數列{an}的前n項和Sn滿足:-（n2+n-1）Sn-（n2+n）=0。

（1）求數列{an}的通項公式an。

分析：本題（1）先求出Sn,由Sn求an是要求,考慮利用裂項求和。

解：（1）由S2n-（n2+n-1）Sn-（n2+n）=0,得[Sn-（n2+n）]（Sn+1）=0。由于{an}是正項數列,所以Sn＞0,Sn=n2+n。于是a1=S1=2,n≥2時,an=Sn-Sn-1=n2+n-（n-1）2-（n-1）=2n。綜上,數列{an}的通項an=2n。

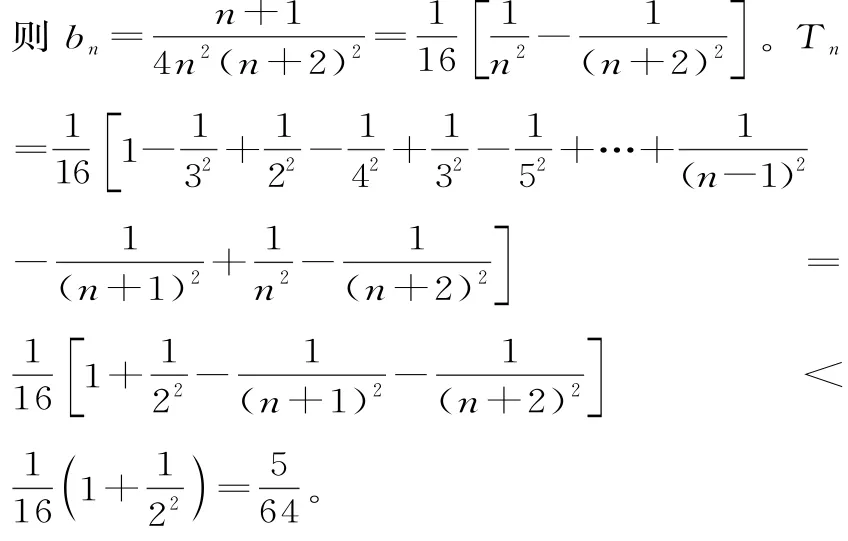
歸納：所謂裂項求和,就是把一個數列的一項分成兩項之差,裂項之后有些是可以互相抵消的,從而求出數列前n項和。可以裂不為0的常數）。裂項時一定要看清哪些項是可以抵消的,哪些項要保留。一般前、后保留的項數是一樣多的,一般會出現相鄰項前后抵消,也可能隔項抵消,這是由相鄰兩個分母的情況來確定的。常見的裂項有現成的模式,不常見的裂項可以先猜后驗,即把分母裂開然后確定分子的情況。

三、領悟基本思想

解得m≥3或m≤-4,所以m的最小值為3。

歸納：在解數列題過程中,函數與方程思想、轉化與化歸思想、分類討論思想等使用頻率都很高,一些有難度的試題往往是在數學思想方法指引下,利用相應的知識方法去求解的。

例7 設數列{an}的前n項和為Sn,對任意的正整數n,都有an=5Sn+1成立,記

（Ⅰ）求數列{an}與數列{bn}的通項公式。

（Ⅱ）設數列{bn}的前n項和為Rn,是否存在正整數k,使得Rk≥4k成立?若存在,找出一個正整數k;若不存在,請說明理由。

（Ⅲ）記cn=b2n-b2n-1（n∈N*）,設數列{cn}的前n項和為Tn,求證:對任意正整數n都有

分析：（Ⅰ）的求解是常用方法,而（Ⅱ）、（Ⅲ）的求解必須具體問題具體分析。由（Ⅱ）的設問,結論不確定,問題主要集中在三個方面:前n項和為Rn,結論形式（存在、不存在）,解題方向方法的選擇。如果直接著手探求,可能要花費大量時間。所以,對探索性問題結論的預判很重要。是否存在呢?先試試16,…,以上“試驗”沒有一次可以佐證存在性,那么解題的方向肯定定位在“證明不存在”。而且,在具體的探求過程中可以發現,每項都可以分解出一個4,后面一項正、負號交替出現,從而為求Rn帶來啟示,特例探求不僅能直接解決一些問題,還可以盡快發現解決復雜問題的方法途徑。由于不可能對數列{bn}求和,需要變形,而符號規律的出現提示,可以兩項復合為一項,適當放縮后,或許就可以得到我們試驗的結論。從而完成由特殊到一般的探索之旅。

有了（Ⅱ）的分析基礎和經驗,（Ⅲ）的證明可以類比,首先確定cn,然后適度合理放縮求和,只定“域”而不是求“值”。

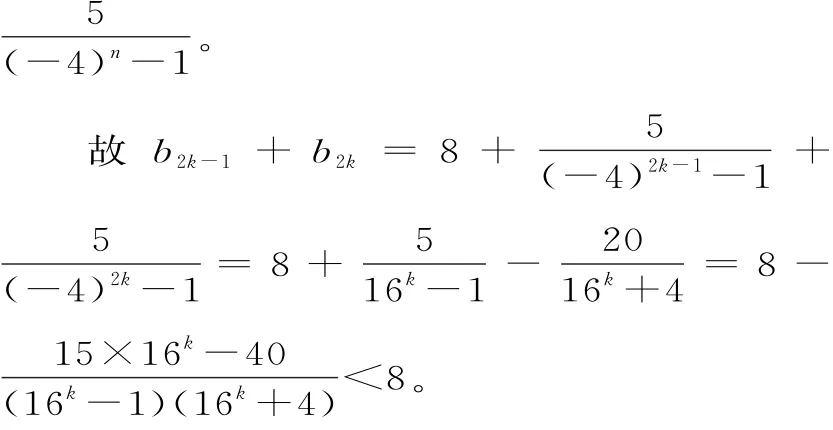
當n為偶數時,設n=2m（m∈N*）,故Rn=（b1+b2）+（b3+b4）+…+（b2m-1+b2m）＜8m=4n。

當n為奇數時,設n=2m-1（m∈N*）,故Rn=（b1+b2）+（b3+b4）+…+（b2m-3+b2m-2）+b2m-1＜8（m-1）+4=8m-4=4n。

所以對于一切的正整數n,都有Rn＜4n。

故不存在正整數k,使得Rk≥4k成立。

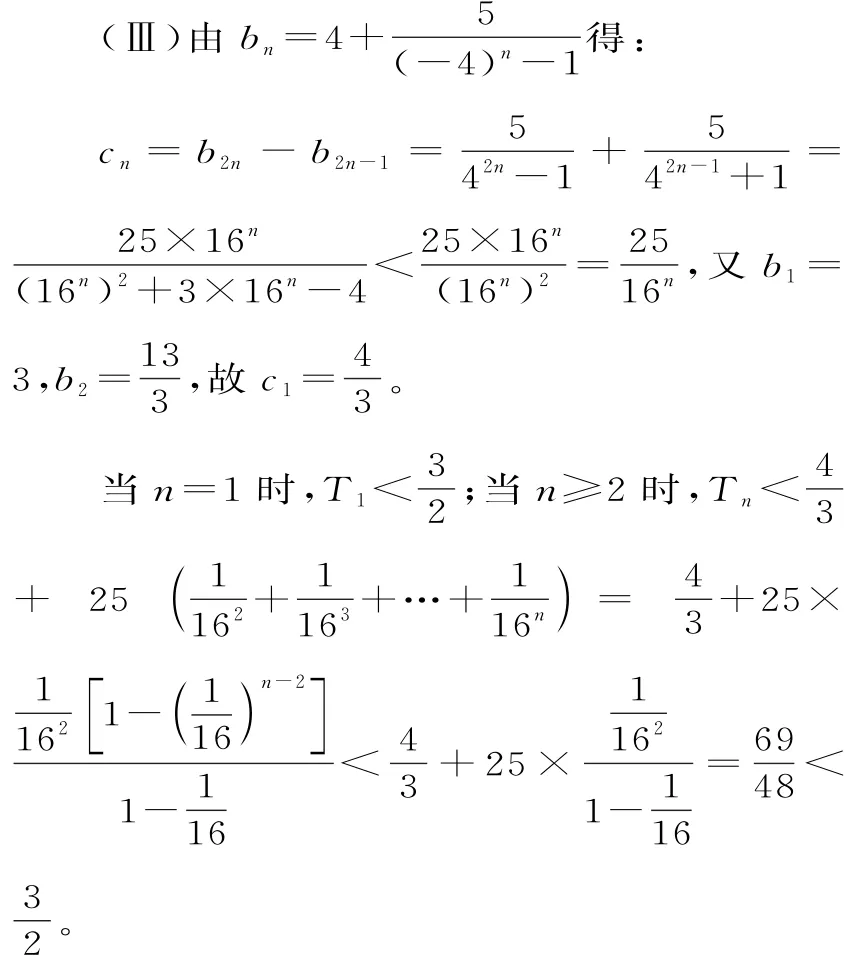
歸納：數列不等式證明問題一般難度較大,主要體現在知識綜合、思維要求高、代數變形較靈活上。比如,常用的數列放縮變形形式有舍掉（或加進）一些項、在分式中放大或縮小分子（分母）、利用基本不等式、根據函數性質、合并后再放縮、固定一部分項（一般是前面的項）放縮另外的項等,突出考查同學們的數學思維能力、分析問題與解決問題的能力。