從一道線性規劃題的錯解說起

廣東省深圳市紅嶺教育集團高中部 馬 鋒

一、題目呈現

二、錯解過程

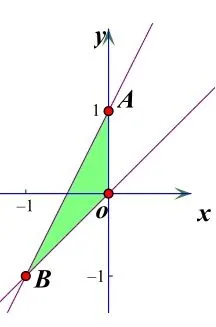
1.由題意畫出可行域，如右圖陰影所示。

2.將邊界端點A（0，1）、B（-1，-1）的坐標代入m。

3.由于邊界AB是虛線，結果應為開區間。

三、分析原因

四、解法剖析

解法一：分類討論思想、轉化思想

1.當x+y=0時，m=0。

（1）當xy=0時，m=1；

點評：此解法是純粹的代數方法，主要是分類討論思想，將目標函數恒等變形為關于斜率的“對勾”函數模型，結合反比例函數性質，最終解決問題。顯然，此方法過程比較煩瑣，運算量比較大，思維細節比較多，出錯的風險自然很大，具有可操作性，但不易算對。

解法二：數形結合思想、轉化思想、分類討論思想

設直線l：x+y=0，過M作l的垂線，記垂足為N，連接OM，記OM的ON夾角為，則

1.當x+y=0時，m=0。

點評：這種解法主要是受到平面內兩個距離公式（即兩點間的距離公式和點到直線的距離公式）的啟發，把目標函數恒等變形，轉化為直角三角形中一個內角的正弦函數來處理。當然，里面也涉及了分類討論思想，但相比解法一顯然要簡潔很多，主要是少了一層討論，運算量明顯減少，出錯風險自然降低不少。

解法三：極坐標，坐標轉化思想

點評：受目標函數形式的啟發，結合極坐標直角坐標互化公式，直接轉化為三角函數的值域問題，妙哉妙哉！此解法巧妙地回避了冗長的分類討論，解法出其不意，運算量非常小，出錯風險極低。

解法四：平面向量轉化思想

點評：受目標函數分子和分母的啟發，結合平面向量的數量積坐標運算，結合恒等變形處理，最終轉化為向量的夾角問題，妙哉妙哉！此解法同樣回避了冗長的分類討論，解法新穎獨特，運算量極低，想出錯都很難！

五、反思小結

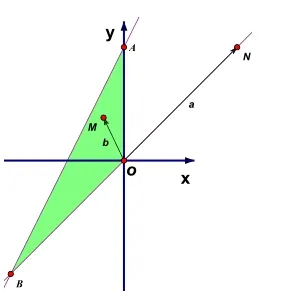
我們再來分析題目本身，求m的范圍其實就是求m的兩個最值，而本題最值的最優解其實有無窮多個，除端點A，B外，只要是可行域內邊界直線x=0（最大值點）和y=x（最小值點）上的點都可以！因此本題采用代入法只會弄巧成拙。進一步思考：約束條件中第三條直線為什么沒取等號呢？實際上，如果此處取了等號，這道題將毫無命題價值，沒有任何檢測意義，學生即便是投機代入，也可以得到最終的結果，這樣將無法揭示學生的思維過程，根本沒有診斷作用，對于教學來說，可以說是一道“費題”！可以料想，第三條邊界直線設置成虛線其實是命題人故意設計的一個“陷阱”，由此我們不難看出命題人的良苦用心，為了暴露代入法的弊端，苦心設計一道這樣的題目，已達到最終拯救“迷途”學生的目的，這個“套”下得真好，讓我們為用心走心的命題人點贊喝彩！這也啟示我們一線的教師，在命題選題時一定要有的放矢，題目務必有針對性和診斷性，以便更好地服務于教學工作。