蒙華鐵路陽城隧道土砂分界地層分界面位置對圍巖穩定性影響探究

王志杰，李瑞堯，徐海巖，唐 力，徐君祥，周 平

(西南交通大學交通隧道工程教育部重點實驗室,四川 成都 610031)

0 引言

蒙華鐵路是我國北煤南運的國家戰略運輸新通道，是國家綜合交通運輸系統的重要組成部分。陽城隧道作為蒙華鐵路關鍵性控制工程之一，地質條件極為復雜，穿越地層包括全風化紅砂巖地層、土砂分界地層和土砂互層地層。隧道在施工階段出現了初期支護開裂變形、掌子面坍塌和涌水涌砂等情況。

國內外學者采用理論分析、數值模擬、現場試驗和室內試驗等方法對軟弱地層隧道圍巖穩定性進行研究。關寶樹[1]針對日本、美國和歐洲等國的隧道開挖方法及隧道開挖工法選擇的基本條件進行了歸納，包括施工條件、圍巖條件、工期和環境條件、隧道斷面面積及埋深等；李國良[2]依托鄭西、寶蘭高鐵，對大斷面黃土隧道臺階法開挖的適用性進行試驗研究，得到采用臺階法一定程度上可加快施工進度的結論；楊建民[3]以鄭西鐵路大斷面黃土隧道為依托，對多種開挖工法進行分析，提出非特殊情況下高速鐵路大斷面黃土隧道宜采用三臺階七步法開挖；張德華等[4]以蘭新鐵路大梁山隧道為工程背景，采用數值模擬、現場試驗等方法對三臺階七步開挖法施工的高地應力隧道支護結構受力進行研究；朱望瑜[5]結合太中銀鐵路土石分界地層隧道施工，通過數值模擬分析了臺階法開挖不同臺階參數對隧道穩定性的影響；楊斌等[6]以互層圍巖為研究對象，將近水平軟硬互層圍巖等效為橫觀各向同性巖層，建立平面應變有限元模型對支護結構受力進行分析，得到了開挖后拱頂及仰拱向內側彎曲的結論；李奎[7]對隧道穿越水平層狀圍巖的壓力拱進行了研究，通過數值模擬探究了雙層圍巖隧道的塑性區分布；黃彬[8]針對隧道穿越黃土土石分界地層大斷面隧道進行了施工技術方面的研究，得到爆破施工的技術要點等。

三臺階七步開挖法在偏壓、高地應力及軟巖地層等不同地層中均有研究[9]，但是在互層圍巖及分界地層中的研究并不全面，尚需要補充。雖已有學者對互層圍巖施工方法進行了研究，包括施工工法對圍巖穩定性的影響、支護參數的設計等[10-15]，但針對分界面的影響尚未有系統研究。本文從分界面入手，通過調整土砂分界地層相對層厚，研究三臺階七步開挖法施工的土砂分界地層隧道圍巖變形、塑性區擴展以及支護結構受力對圍巖穩定性的影響。

1 工程概況

陽城隧道位于蒙華鐵路浩勒報吉至三門峽段，地理位置處于陜西省榆林市靖邊縣附近，起訖里程為DK242+041～DK249+134，全長7 093 m，最大埋深約207 m，設計時速120 km。陽城隧道為單洞雙線隧道，開挖斷面在100 m2以上，屬大斷面隧道。

隧道地層巖性主要為第四系上更新統風積(Q3eol)砂質新黃土及黏質新黃土、第四系中更新統沖洪積(Q2al+pl)中砂、白堊系下統洛河組(K1l)砂巖。其中，土砂分界地層下部為全風化砂，上部為砂質新黃土局部夾塊石，掌子面素描圖及現場圖如圖1所示。

(a) 掌子面素描圖1 (b) 掌子面現場圖1 (c) 掌子面素描圖2 (d) 掌子面現場圖2

圖1掌子面素描圖及現場圖
Fig.1 Sketches of tunnel face and site photos

2 初期支護開裂變形

2017年10月15日01：00時，陽城隧道大里程段在臺階平整過程中發現中臺階左側拱腳處局部發生涌水涌砂。為保證施工安全，立即對初期支護進行支撐加固，約04：00，DK245+270左側邊墻位置處初期支護開裂，并有發展趨勢，后期對變形段進行反壓回填、壓密注漿和逐榀換拱等措施，變形得以控制。變形段為土砂分界地層，右側為強風化砂巖夾塊石、左側為土層夾砂層，圍巖由Ⅴ級調整為Ⅵ級，采用三臺階七步開挖法進行施工，開挖過程中邊墻及掌子面無法自穩，發生涌水涌砂現象，且掌子面發生溜塌及核心土后移；初期支護沉降及收斂較大，控制難度大。涌水、涌砂及圍巖變形相關圖片如圖2所示。

(a) 涌水涌砂 (b) 溜塌 (c) 初期支護開裂變形

圖2涌水、涌砂及圍巖變形相關圖片
Fig.2 Photos of water gushing,sand gushing and surrounding rock deformation

通過分析土砂分界地層圍巖變形機制，除了地層圍巖強度分布不均、砂巖遇水易崩解坍塌等造成大變形的主觀因素，對土砂分界地層圍巖的認識不足也使得隧道在設計施工中出現問題。基于此，本文采用現場試驗、室內試驗及數值試驗等研究方式對土砂分界地層圍巖穩定性進行探究，重點探討地層種類及其厚度變化對圍巖變形、圍巖塑性區及支護結構受力的影響。

3 室內基本物理性能試驗

本次研究的土砂分界地層為上土下砂地層，砂層為全風化砂巖夾塊石，土層為砂質新黃土夾薄砂層。對天然黃土及全風化砂巖進行風干并測定含水率，進行篩分試驗及顆粒密度試驗；同時選取原狀黃土和全風化砂巖進行固結試驗、直剪試驗和三軸試驗，測得其壓縮模量、黏聚力及內摩擦角。土砂分界地層基本物理力學試驗如圖3所示，基本物理參數如表1所示。

(a) 黃土風干 (b) 篩分試驗 (c) 顆粒密度試驗 (d) 三軸試驗 (e) 固結試驗 (f) 直剪試驗

圖3土砂分界地層基本物理力學試驗
Fig.3 Basic physic-mechanical test for soil-sand strata

表1 土砂分界地層基本物理參數Table 1 Basic physic-mechanical parameters of soil-sand strata

4 數值試驗

4.1 建立模型

將隧道穿越的圍巖稱為主層圍巖，隧道拱頂至地表之間的圍巖稱為上覆地層，隧道仰拱拱底以下的圍巖稱為下伏地層，如圖4所示。本次計算將土砂分界地層簡化成上部為砂質黃土、下部為全風化紅砂巖的分界地層。假定水平土砂分界地層土層與砂層黏結牢固且不產生滑移，即土層間的變形滿足連續性。

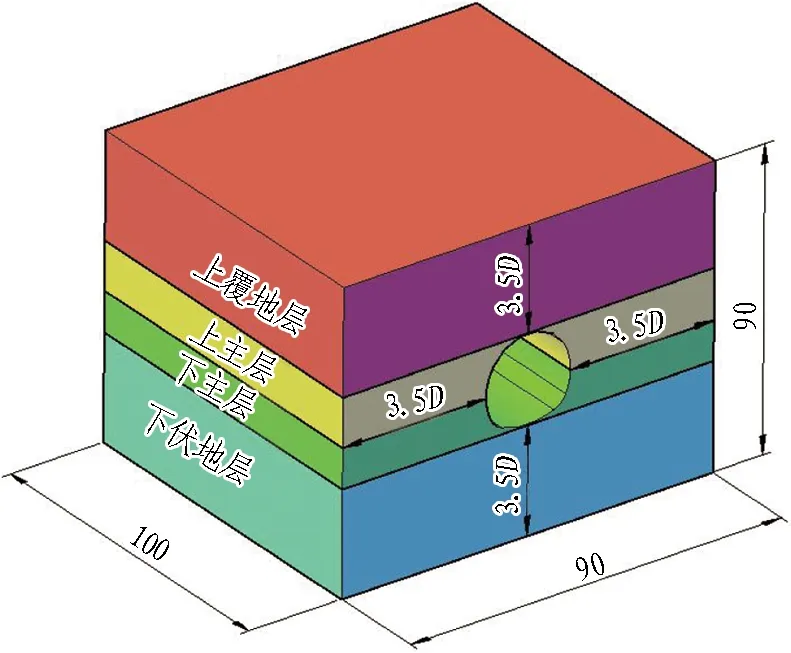
圖4 計算模型示意(單位：m)Fig.4 Calculation model (unit: m)

采用有限差分軟件FLAC3D進行數值模擬，土層采用彈塑性有限元模型，應用Mohr-Coulomb屈服準則，支護結構采用Elastic模型。模型尺寸如圖4所示，計算參數見表2。為充分模擬現場初期的施工情況，隧道開挖方法采用與現場一致的三臺階七步法，開挖后立即支護，施工工序及參數見圖5。

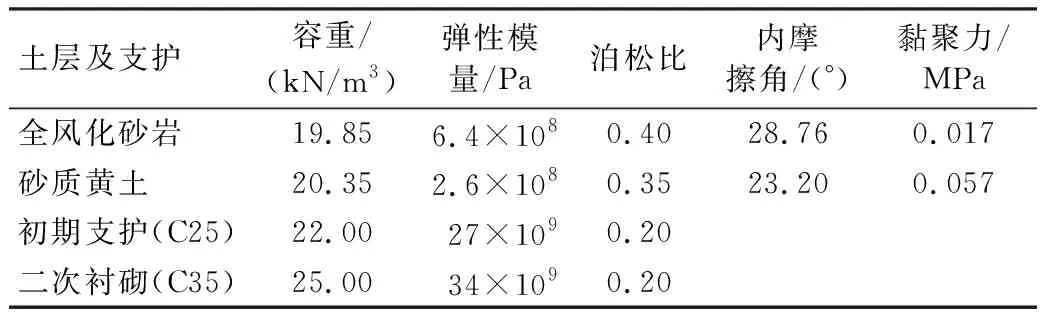
表2 計算參數Table 2 Calculation parameters

圖5 隧道三臺階七步開挖法示意(單位：cm)Fig.5 Sketch of three-bench seven-step excavation method for tunnel (unit: cm)

4.1.1 不同組合地質條件下的受力和變形

主要以水平雙主層地層為對象進行詳細分析，地層分類及其示意圖分別見表3和圖6。

表3 土砂分界地層類別Table 3 Classification of soil-sand strata

注：括號內比例為主層占掌子面厚度的百分比，如1∶3模型為掌子面處25%黃土+75%紅砂巖。

(a) 1∶0/0∶1模型 (b) 1∶3模型 (c) 1∶1模型 (d) 3∶1模型

圖6土砂分界地層類別示意
Fig.6 Sketches of classification of soil-sand strata

隧道貫通后斷面主應力分布如圖7所示。由圖可知，隧道貫通后不同地層分類下主應力分布范圍有著很大的區別，由于三臺階七步法開挖的左右側存在時間上的差異性，模型中左側為先開挖部分，應力集中區域均在左側位置，同時可以明顯看出分界地層應力集中區域較大，且1∶3模型和3∶1模型產生了明顯的“下垂”型的分布情況。

(a) 1∶1模型 (b) 3∶1模型

(c) 1∶3模型 (d) 1∶0/0∶1模型

圖7隧道貫通后某斷面應力云圖
Fig.7 Stress nephograms of a section after tunnel breakthrough

4.1.2 測點布置

圍巖監測點主要包含拱頂、拱肩、拱腰、拱底、各分層面與各臺階底部；初期支護應力監測點包含拱頂、拱腰、拱底、各臺階處和各分層面。監測點布置如圖8所示。

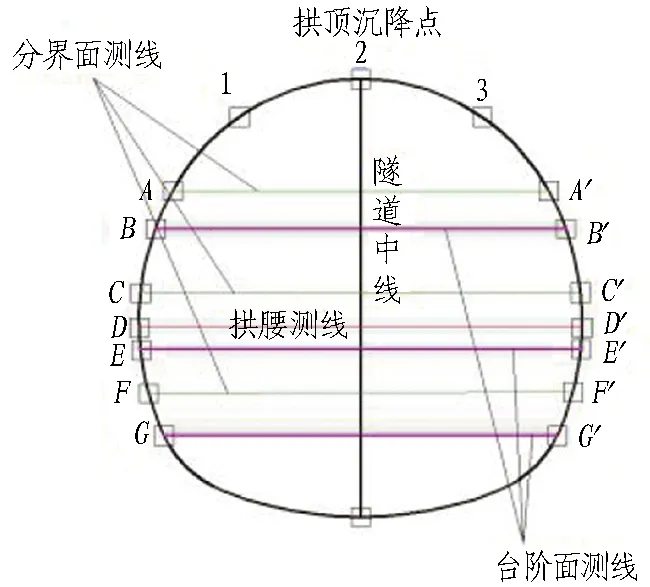
(a)圍巖變形監測點

(b)初期支護應力監測點

4.2 1∶0-1∶1-0∶1模型圍巖穩定性探究

如圖8所示，對圍巖變形及初期支護應力進行監測，以探究圍巖的穩定性。首先對1∶0、0∶1及1∶1模型進行分析，對比砂質新黃土、全風化砂巖及二者1∶1土砂分界地層圍巖穩定性，以探究不同類型地層圍巖穩定性差異。

4.2.1 圍巖變形分析

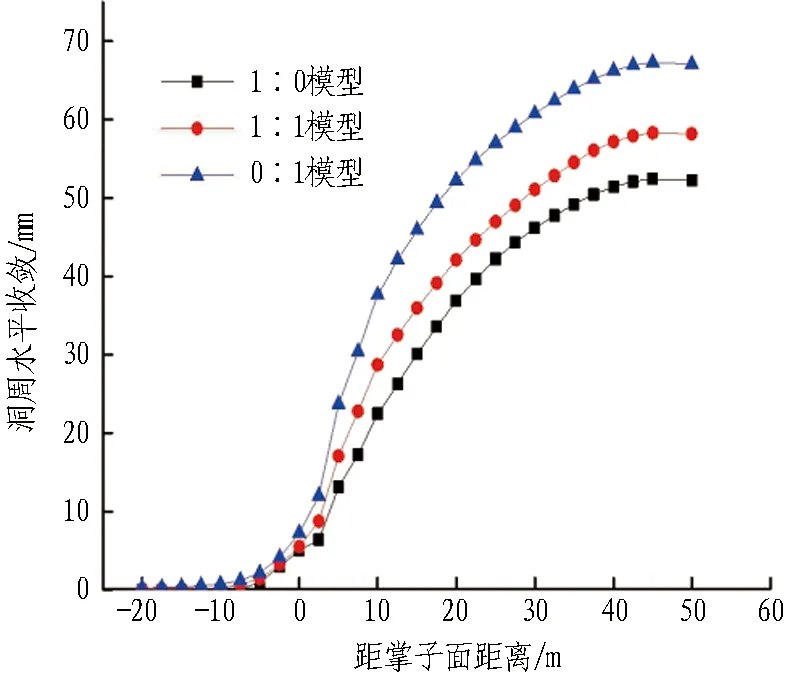
1∶0-1∶1-0∶1模型土砂分界圍巖變形時程曲線如圖9所示。由圖可知：1)上臺階弧形導坑開挖后，監測斷面收斂增長迅速，隨著進一步開挖，拱頂沉降發展，上臺階初期支護完成后變形減緩，仰拱封閉后，凈空收斂基本達到穩定。 2)對比3個模型的圍巖變形，洞周收斂和拱頂沉降：0∶1模型>1∶1模型>1∶0模型。 3)隨著隧道的開挖，3種模型沉降趨于穩定的時間并不一致，明顯觀察到由于土層改變而產生“穩定滯后”，這一現象主要表現在拱頂沉降上，洞周收斂則沒有明顯的滯后情況，1∶0模型在核心土開挖前已趨于穩定，0∶1模型在仰拱封閉成環后趨于穩定，而1∶1模型正好處于上述2個模型中間、在核心土開挖完成后趨于穩定。

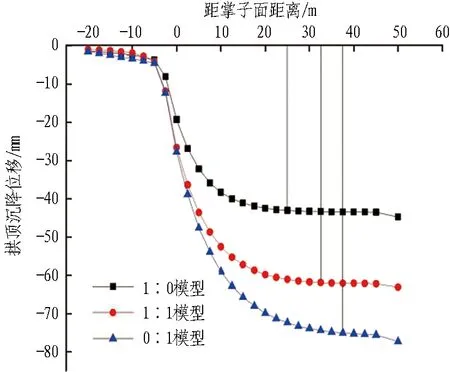
(a)拱頂沉降時程曲線

(b)拱腰收斂時程曲線

本研究中土的黏聚力優于砂，但其彈性模量和內摩擦角均劣于砂。土的變形主要由較小的彈性模量來影響，而砂由于黏聚力較小，造成的塑性流動對收斂值造成了較大的影響。綜合考慮，在變形性質方面，砂是劣于土的。圍巖各臺階變形時程曲線及40 m斷面處圍巖變形最終收斂值分別見圖10和表4。

圖10 1∶0-1∶1-0∶1模型土砂分界圍巖各臺階變形時程曲線Fig.10 Time-history curves of bench deformation of surrounding rock in 1∶0-1∶1-0∶1 model of soil-sand strata

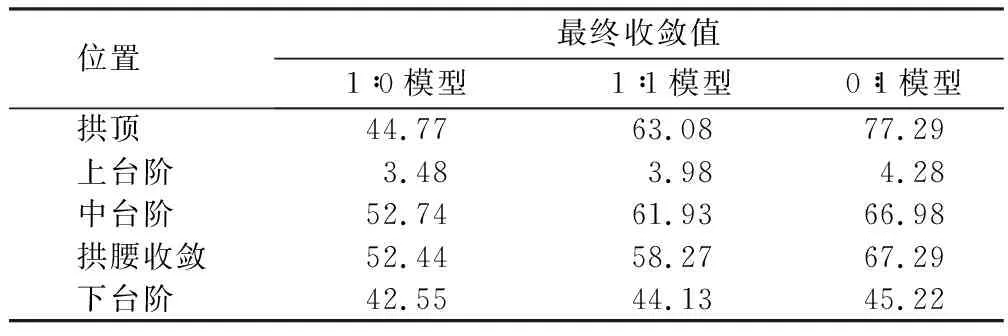
表4 1∶0-1∶1-0∶1模型40 m斷面處圍巖變形最終收斂值Table 4 Final convergences of surrounding rock deformation at 40 m cross-section in 1∶0-1∶1-0∶1 model mm

由圖10可得：1)上、中、下3個臺階處，上臺階的收斂最小，下臺階次之，中臺階最大；2)上、中、下臺階處的收斂，1∶0模型小于0∶1模型，在變形性質方面，全土地層優于全砂地層；3)1∶1模型，各個臺階處的收斂值均處于全土和全砂之間，相比于全土地層，各收斂值更接近全砂地層。

全土地層水平收斂大于拱頂沉降，應著重對邊墻處進行加固；其他地層除拱頂處需要監測并加固外，在拱腰處也應進行加固處理。

表5所示為施工各階段變形占總變形量的百分比。由表可以得到，上、中臺階的開挖對拱頂沉降影響較大，中、下臺階、核心土開挖對水平收斂影響較大。

表5 1∶0-1∶1-0∶1模型各施工階段變形占總變形量的百分比Table 5 Proportions of deformation of every construction phases in 1∶0-1∶1-0∶1 model in total deformation

4.2.2 圍巖塑性區分析

表6所示為三臺階七步法各工序下隧道圍巖塑性區變化。由表可知：1)1∶0模型(全土地層)，上臺階開挖后，掌子面范圍內邊墻位置出現剪切塑性區；隨著中臺階左側土體開挖(見表6中第2步)，拱腳和拱底處出現了剪切塑性區，核心土出現了拉伸塑性區；隨著開挖，拱肩處出現了剪切塑性區，拱腳處的塑性區逐漸向邊墻處擴展，最終拱腳和拱底處產生的塑性區深度約為6 m。2)0∶1模型(全砂地層)，開挖前拱部處出現剪切塑性區；隨著開挖進行，兩側拱腳處出現剪切塑性區，向邊墻處擴展，最終塑性區深度最大處為邊墻位置，為4 m。3)1∶1模型(土砂分界地層)，塑性區的發展由拱肩和拱腳處逐漸向邊墻處延伸。4)單一地層中，全砂地層的塑性區發展較早，但是全土地層的發展較快；不同于單一地層模型，1∶1模型在第3、4步中，分界面處圍巖先出現塑性區，且1∶1模型的最終塑性區分布與0∶1模型更為接近，與前述變形分析中“1∶1模型位移值與0∶1模型更為接近”的結論相同。

表6 三臺階七步法各工序下隧道圍巖塑性區變化Table 6 Variations of surrounding rock plastic zone under different construction sequences of three-bench seven-step method

注：0表示開挖到掌子面前方；1表示開挖上部弧形導坑；2表示開挖中臺階左側；3表示開挖中臺階右側；4表示開挖下臺階左側；5表示開挖下臺階右側；6表示開挖核心土；7表示開挖仰拱。同表9。

4.2.3 支護結構應力分析

隧道支護結構受力直接影響隧道施工安全，初期支護應力曲線如圖11所示。

由圖11可知，土砂分界地層支護結構產生的最大主應力(不論是拉應力還是壓應力)均較小，主應力差隨著土層向砂層的轉化(1∶0-1∶1-0∶1)逐漸減小，且在拱頂處受較大的拉力。前文對比分析了1∶1土砂分界地層與單一地層圍巖穩定性，下文將在所得結果基礎上改變土層與砂層相對厚度比，對土砂分界地層圍巖穩定性進行探究。

(a) 各臺階處最大主應力 (b) 各臺階處主應力差 (c) 拱頂處主應力

圖11土砂分界支護結構應力曲線
Fig.11 Stress curves of supporting structure in soil-sand strata

4.3 1∶3-1∶1-3∶1模型圍巖穩定性探究

在1∶1模型的基礎上，設置1∶3模型和3∶1模型，探究土砂分界地層土層與砂層相對厚度對圍巖穩定性的影響，分析其圍巖變形、塑性區擴展及支護結構受力變化。

4.3.1 圍巖變形分析

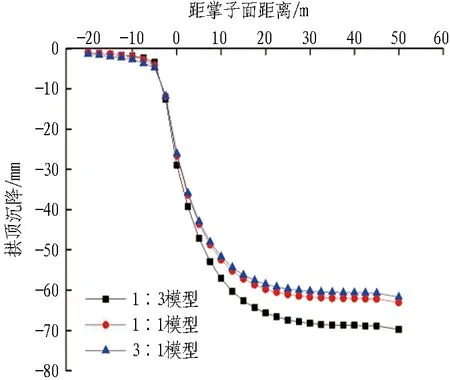
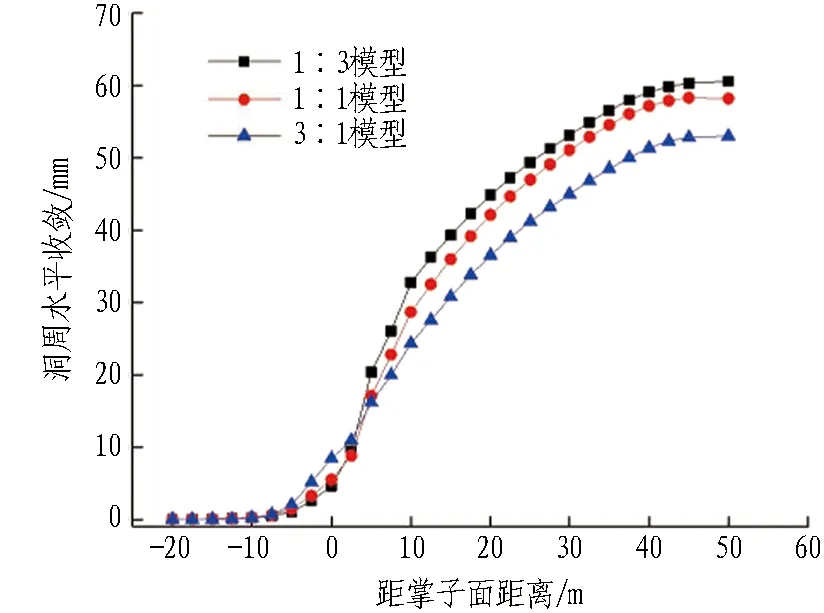
1∶3-1∶1-3∶1模型土砂分界圍巖變形時程曲線如圖12所示。由圖可知：1)拱頂沉降的趨勢與前述結果一致，但是不同相對厚度比的土砂分界地層，沉降趨于穩定的時間并不一致，1∶1模型和1∶3模型在核心土開挖前趨于穩定，而3∶1模型沉降趨于穩定在35 m左右，即核心土開挖后。 2)拱頂沉降與洞周收斂位移值為1∶3模型>1∶1模型>3∶1模型。 3)軟硬互層圍巖的性質取決于較軟弱圍巖。如前所述，在黏聚力上砂劣于土，1∶1模型洞周收斂與0∶1模型接近；在彈性模量上土劣于砂，1∶1模型拱頂沉降與1∶0模型更為接近。3∶1模型由于掌子面土占的比例更大、土對拱頂沉降影響較大，其拱頂沉降與1∶1模型較為接近；而1∶3模型由于掌子面砂占的比例更大、砂對水平收斂影響較大，其洞周收斂與1∶1模型更為接近。土砂分界地層圍巖各臺階變形時程曲線及40 m斷面處圍巖變形最終收斂值分別如圖13和表7所示。

(a) 拱頂沉降時程曲線

(b) 拱腰收斂時程曲線

圖13 1∶3-1∶1-3∶1模型土砂分界圍巖各臺階變形時程曲線Fig.13 Time-history curves of bench deformation of surrounding rock in 1∶3-1∶1-3∶1 model of soil-sand strata

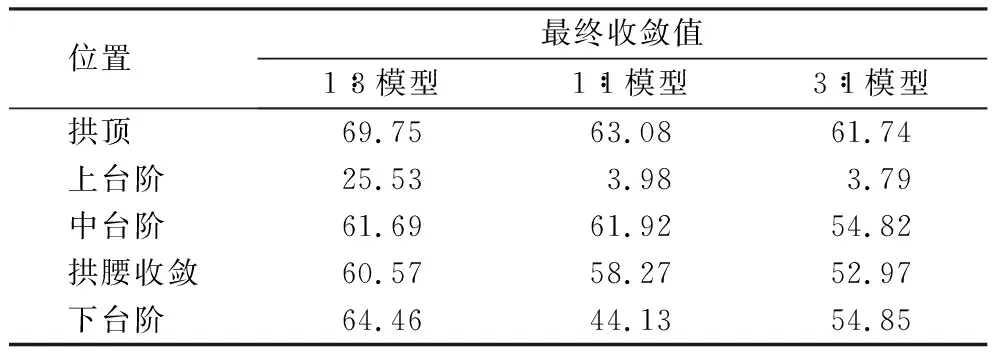
表7 1∶3-1∶1-3∶1模型40 m斷面處圍巖變形最終收斂值Table 7 Final convergences of surrounding rock deformation at 40 m cross-section in 1∶3-1∶1-3∶1 model mm

圖13中，1∶3、1∶1、3∶1模型土砂分界面分別位于上臺階、中臺階及下臺階處。分析圖13和表7可得：1)1∶3模型上、中、下臺階的洞周收斂均大于其他2個模型，且下臺階處位移明顯大于中臺階處。 2)1∶0、1∶1及0∶1模型洞周收斂為：中臺階>下臺階>上臺階，而1∶3模型和3∶1模型洞周收斂位移為：下臺階處>中臺階處>上臺階處。 3)上臺階水平收斂，1∶3模型>1∶1模型>3∶1模型；中臺階水平收斂，1∶3模型>1∶1模型>3∶1模型；下臺階水平收斂，1∶3模型>3∶1模型>1∶1模型。 4)3∶1模型，由于分界面出現在下臺階，出現了變形突變的情況；1∶3模型，由于分界面的存在，上臺階處水平收斂明顯大于另外兩者。同樣在中臺階處，1∶1模型的水平收斂也較另外兩者大。 5)隨著分界面下移，即掌子面土比例逐漸增大，除去分界面所處位置的突變情況，其余2個模型均因分界面下移使得各項凈空收斂在減小。 6)隨著分界面上移(3∶1-1∶1-1∶3)，洞周收斂與拱頂沉降之間的差值逐漸縮小。

由以上分析得出：分界面位置處變形均較突出，故需要在分界面位置處進行加固處理；分界面位置對拱頂沉降與洞周收斂間的相互關系有一定影響。

表8所示為各施工階段變形占總變形量的百分比。由表可以得到，拱頂沉降大都集中在上、中臺階開挖，中臺階開挖對洞周收斂的影響最大。從1∶3-1∶1-3∶1模型，分界面逐漸下移，上、中臺階開挖造成的水平收斂速率逐漸減小，下臺階和核心土開挖造成的收斂速率逐漸增大，仰拱封閉前洞周收斂和拱頂沉降均達到了98%以上。隧道開挖過程中分界地層分界面位置對收斂速率有一定影響，接近土層分界面位置的收斂速率較大，但并不改變中臺階開挖對洞周收斂影響最大的結論。

4.3.2 圍巖塑性區分析

表9所示為三臺階七步法不同施工工序下隧道圍巖塑性區變化。由表可得：1)1∶3模型在上臺階開挖后，核心土上部出現拉伸塑性區、下部僅有剪切塑性區；中臺階左側開挖，拱腳處出現塑性區，中臺階開挖完成后迅速在分界面下側形成較長范圍塑性區，拱腳處塑性區也加速擴展；核心土開挖前，分界面下側塑性區已從深度2 m擴展到4 m；隧道貫通后，從拱腳到分界面處產生深度超過4 m的塑性區，范圍與拱底相當。2)3∶1模型在第3步時，在左邊墻、右拱腳及右拱肩處出現塑性區，第4步中(開挖下臺階左側時)分界面上部邊墻處、下部拱腳處塑性區迅速擴展，最終在拱底到兩側拱肩間形成深度2 m以上的塑性區。3)相比于1∶1模型，1∶3模型和3∶1模型在分界面附近邊墻處塑性區的發展較早且迅速，1∶3模型邊墻塑性區在第2—4步中發展迅速，3∶1模型邊墻塑性區在第3—4步中發展迅速，而1∶1模型邊墻塑性區在第4—5步中發展迅速。4)3個分界地層模型中，1∶3模型塑性區深度最大且發展最快。

表8 1∶3-1∶1-3∶1模型各施工階段變形占總變形量的百分比Table 8 Proportions of deformation of every construction phase in 1∶3-1∶1-3∶1 model in total deformation

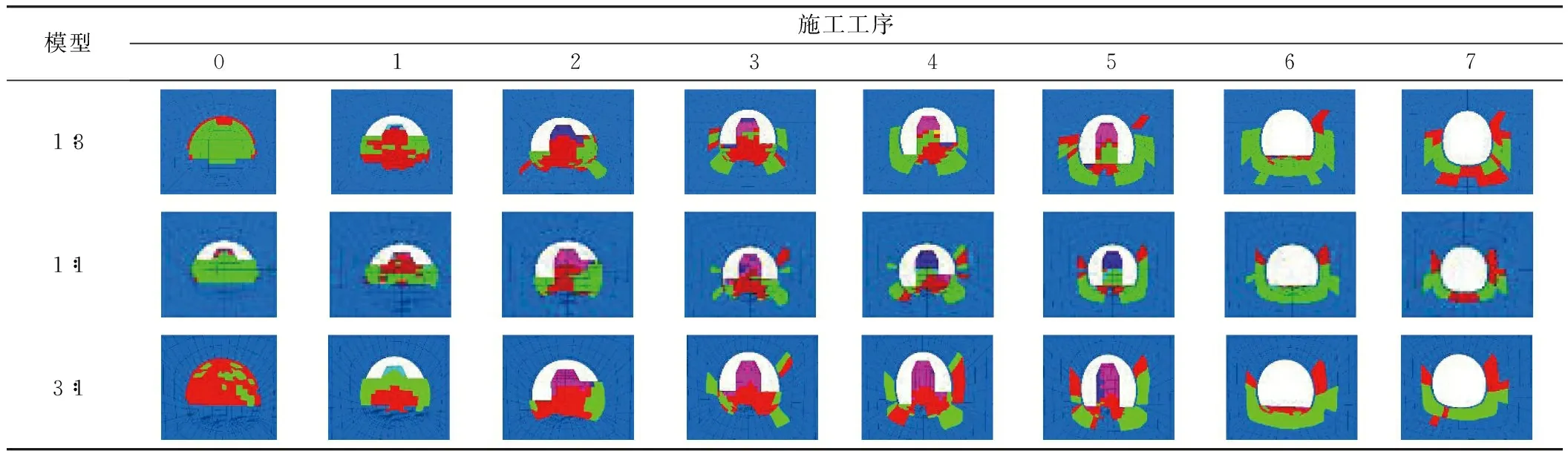
表9 1∶3-1∶1-3∶1模型各工序下隧道圍巖塑性區變化Table 9 Variations of surrounding rock plastic zone under different construction sequences in 1∶3-1∶1-3∶1 model

4.3.3 支護結構應力分析

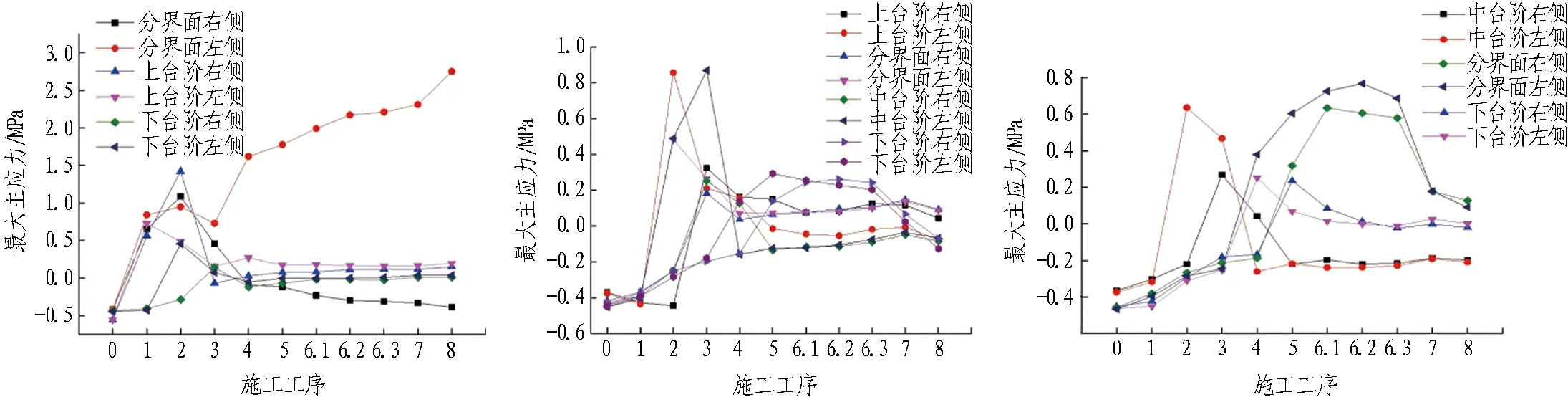
隨著土砂分界面的下移，中臺階、下臺階處初期支護最小主應力不斷減小，上臺階處最小主應力不斷增大。支護結構最大主應力隨施工工序變化曲線見圖14。

(a) 1∶3模型 (b) 1∶1模型 (c) 3∶1模型

圖14支護結構最大主應力隨施工工序變化曲線
Fig.14 Variation curves of maximum principal stresses of supporting structure with construction procedures

由圖14可得：1)3個模型均在分界面處會產生拉應力。2)觀察圖(a)會發現，在分界面處左側(先開挖側)產生了持續增長的拉應力，而在右側則產生了很大的壓應力，且分界面所在位置產生的拉應力遠大于上臺階、拱腰處；圖(c)中，分界面所在位置支護結構產生的拉應力也超過了其附近中臺階和拱腳處的值。3)觀察三者的最大主應力變化趨勢，1∶1模型中的上臺階和下臺階分別在第2、3步和第5、6.1步達到峰值，平均值分別為0.6 MPa和0.25 MPa；1∶3模型中的上臺階在第1、2步工序時達到峰值，平均值為1 MPa；3∶1模型中的下臺階最大主應力峰值出現在第4、5步，平均值為0.7 MPa左右，分界面的存在影響到了應力發展。

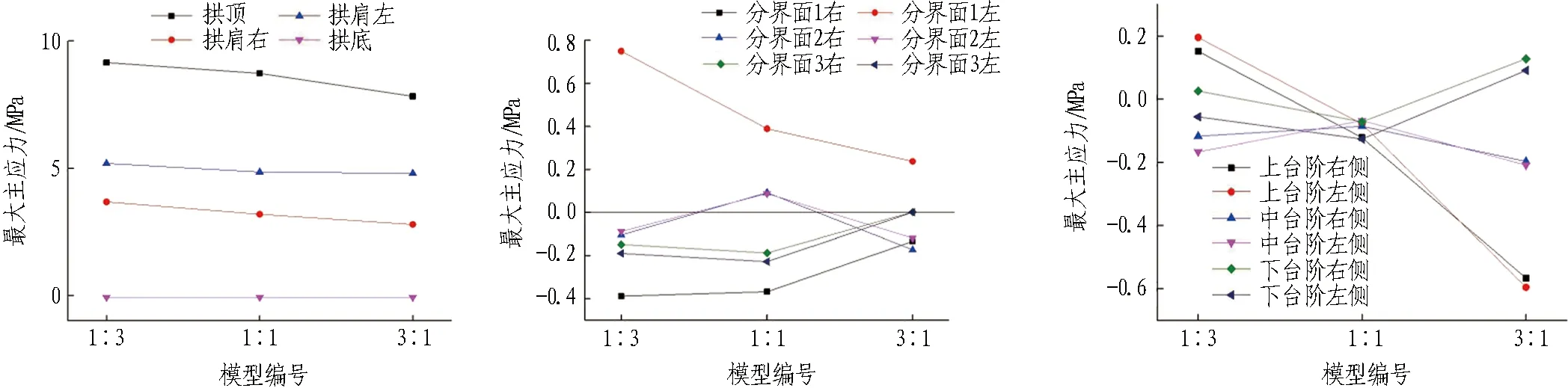
支護結構最大主應力如圖15所示。由圖可知：1)1∶3-1∶1-3∶1模型，拱頂、拱肩、拱底處的最大主應力呈現減小的趨勢。2)相比較其他模型而言，分界處及其所在臺階處的支護結構最大主應力較大。

綜上，由于分界面的存在，對分界面處及所在臺階位置的初期支護結構的應力產生了較大的影響，在施工過程中需要對分界面位置進行重點監測。

(a) 拱頂、拱底最大主應力 (b) 分界面處最大主應力 (c) 臺階處最大主應力

圖15支護結構最大主應力
Fig.15 Maximum principal stresses of supporting structure

5 現場監控量測試驗

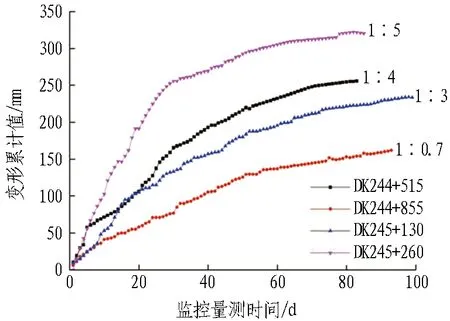
選取陽城隧道1#斜井正洞小里程方向，監控量測斷面為DK244+855、DK244+515、DK245+130和DK245+260。DK244+855斷面上層為砂質新黃土，約占掌子面的60%；下層為富水全風化紅砂巖，約占40%。DK244+515斷面，掌子面上部分布有少量的砂質黃土，約占25%；下部為全風化砂巖夾塊石。DK245+130斷面，掌子面上部為土夾薄砂層，占20%；下部為全風化紅砂巖。DK245+260斷面，掌子面上部為砂質老黃土，占16%；下部為全風化砂巖夾少量塊石。現場沉降監控量測如圖16和表10所示。

(a) 拱頂沉降時態曲線

(b) 拱腰收斂時態曲線

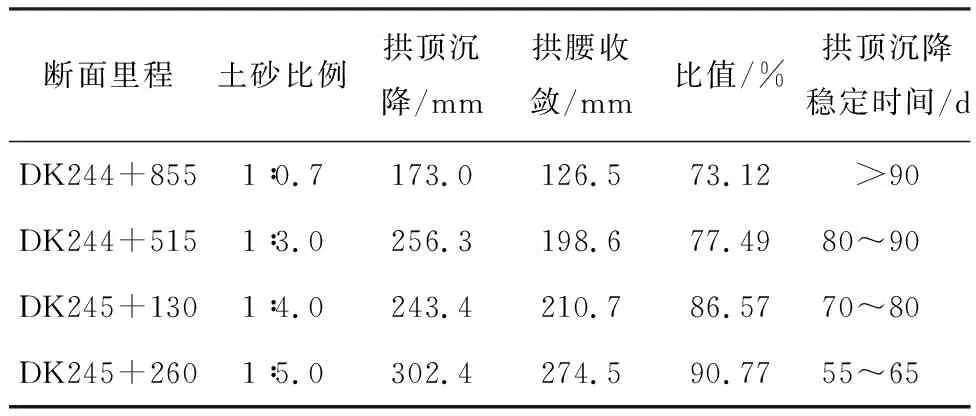
表10 各斷面沉降收斂值Table 10 Final convergences of every cross-section

注：比值=拱腰收斂/拱頂沉降×100%。

由表10可知，監控量測結果與數值模擬結果規律相同，即隨著分界面的下移(即土占的比例的增多)，初期支護的變形在減小，且隨著分界面的上移，拱頂沉降和水平收斂的差距在不斷減小，與數值模擬規律相類似，印證了前文中所述的“穩定滯后”現象的存在。鋼拱架鋼筋應力最大值如表11所示，隨著分界面的上移，拱底、拱頂鋼拱架內力值增大，與前述的規律相同。

表11 鋼拱架鋼筋應力最大值Table 11 Maximum stress of reinforced bars of steel frame

6 結論與討論

鐵路大斷面隧道穿越土砂分界地層，洞周圍巖變形及初期支護內力與土砂分界的土石比例有著密切的聯系，通過分析可知：

1)土砂分界地層分界面的存在對圍巖周圍的主應力分布產生了較大的影響，產生了不同程度的“下垂”狀態。當從全土層向全砂層轉變，拱頂沉降出現了“穩定滯后”的現象。分界地層相比于單一地層，在開挖分界面位置處邊墻極易出現塑性變形，產生塑性區。

2)針對分界面位置的改變，對照監控量測數據，可以看出實際工程中結構收斂與數值模擬規律相同。即隨著全風化砂占的比例的增大，拱頂沉降和洞周收斂都在變大，且部分水平收斂與拱頂沉降的差值會越來越小，甚至是超過拱頂沉降值。

3)開挖模擬中，相比于其他地層條件下相同位置，分界面所處的位置處會產生較大的水平收斂，且分界面處會極易產生拉應力。分界面的存在對于支護結構的應力發展產生了較大的影響，主要體現在到達峰值的時機。

4)當分界面出現在掌子面上部時，支護結構會產生極大應力和較大的變形，圍巖會產生極大的塑性變形，且邊墻部位的塑性區發展迅速。

5)三臺階七步法開挖過程中，拱頂沉降發展主要集中在上、中臺階開挖階段，而水平收斂發展主要在中臺階開挖階段；分界面的下移會導致上、中臺階開挖造成的水平收斂速率減小，使下臺階開挖造成的水平收斂速率增大；由于開挖順序的影響，左側和右側應力分布會產生較大的差異。施工過程中可根據左右側土體的差異來調整左右開挖順序。

6)本文僅針對分界地層下的層厚比進行了研究，僅對分界地層圍巖穩定性進行了定性分析，關于定量分析還需要今后進一步研究。