基于貝葉斯網(wǎng)絡的MEC隨機任務遷移算法

薛 寧 霍 如 劉 江

1 北京工業(yè)大學北京未來網(wǎng)絡科技高精尖創(chuàng)新中心 北京 100124

2 北京郵電大學網(wǎng)絡與交換技術國家重點實驗室 北京 100876

引言

近年來，移動互聯(lián)網(wǎng)和物聯(lián)網(wǎng)兩大網(wǎng)絡得到了快速發(fā)展，對網(wǎng)絡的時延、可靠性提出了更高的要求，而移動邊緣計算(Mobile-edge Computing，MEC)由于其靠近用戶的特性，可以為用戶提供更低時延、更可靠的網(wǎng)絡體驗[1]。在移動邊緣計算的場景下，用戶和服務器的距離很近，數(shù)據(jù)的傳輸速率會很快，在處理任務時既可以利用服務器強大的計算能力又可以節(jié)省移動設備的資源消耗。因此，移動設備更傾向于向MEC服務器遷移任務從而提高任務的執(zhí)行性能，降低任務在移動設備上的開銷。這種變化使得移動設備計算任務的遷移算法變得十分重要。

學術界在任務遷移方面有一定的研究成果，文獻[2]將一個應用劃分為一組有數(shù)據(jù)依賴關系的子任務，通過將子任務間共同需要的數(shù)據(jù)在移動端和服務器各存一份的方式來減少傳輸能耗。但是，在真實環(huán)境中是無法預知子任務間共同需要的數(shù)據(jù)的。文獻[3-5]則提出對多個隨機任務的調(diào)度遷移策略進行優(yōu)化，利用MDP理論、Lyapunov優(yōu)化算法以最小化移動設備能耗和執(zhí)行時延為目標來決策調(diào)度策略。然而在真實場景中部分任務需要和移動設備進行交互而必須在本地執(zhí)行，并且子任務之間是存在關聯(lián)性的，使得調(diào)度策略無法達到能耗和時延最小化的目標。所以本文首先將應用轉換為包含多個子任務的有向圖，從而表征應用本身子任務間的內(nèi)在聯(lián)系，在此基礎上提出了一種基于貝葉斯網(wǎng)的隨機任務遷移算法，利用子任務之間的依賴關系預估每一個子任務執(zhí)行兩種遷移決策所產(chǎn)生的能耗，并得出每個子任務執(zhí)行兩種遷移決策的先驗概率，最后根據(jù)先驗概率以移動設備能耗最小化為優(yōu)化目標生成一組調(diào)度策略。

1 系統(tǒng)模型

本文考慮的MEC系統(tǒng)模型如圖1所示，包含一個移動設備和一個MEC服務器。移動設備是由遷移決策單元、本地處理單元和傳輸單元組成，移動設備通過傳輸單元將一些計算密集型的計算任務遷移到MEC服務器上執(zhí)行，以解決移動終端計算能力有限的問題。MEC服務器是一個部署在無線接入點處并安裝了小型數(shù)據(jù)中心的虛擬機設備，可以為移動設備提供強大的IT服務[6]。

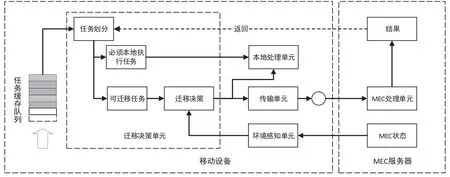
圖1 單用戶MEC系統(tǒng)場景圖

1.1 任務模型

圖2所展示的是一個應用的細粒度任務劃分圖，本文將應用劃分為多個獨立執(zhí)行的子任務，并用一個有向圖來表示[2]。圖2中的節(jié)點表示分割出來的子任務，圖2中的邊表示任務之間的傳輸數(shù)據(jù)，例如：表示任務執(zhí)行完成后，會傳輸?shù)臄?shù)據(jù)給任務而任務只有在接受到任務執(zhí)行完后傳輸過來的數(shù)據(jù)，才能開始執(zhí)行。圖2中的子任務可以分成兩類：一類是必須本地執(zhí)行的任務，如圖中的實心任務0、5表示為另一類為可遷移任務，如圖中的空心任務1、2、3、4，表示為

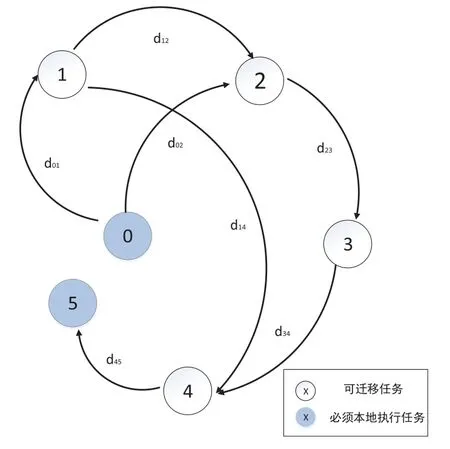
圖2 細粒度任務劃分圖

1.2 計算模型

由于執(zhí)行任務的能耗與任務在移動設備執(zhí)行還是被遷移到MEC服務器執(zhí)行有關，所以本文定義表示任務執(zhí)行位置：

由于執(zhí)行任務的能耗與該任務的前置任務的執(zhí)行位置有關，當此任務及其前置任務都在同一位置執(zhí)行時，兩個任務之間的數(shù)據(jù)傳輸消耗可以忽略不計。所以本文定義表示一個任務的前置任務的執(zhí)行位置和該任務的執(zhí)行位置：

假設移動設備配備單核CPU和一個數(shù)據(jù)傳輸單元，執(zhí)行任務時CPU的頻率為其功率為空閑時CPU的功率為數(shù)據(jù)傳輸單元發(fā)送功率為發(fā)送速率為接收功率為接收速率為MEC服務器執(zhí)行任務時CPU的頻率為為任務的計算量，單位為(CPU cycles)。表示任務執(zhí)行完成后，會傳輸?shù)臄?shù)據(jù)給任務，單位為(bites)。

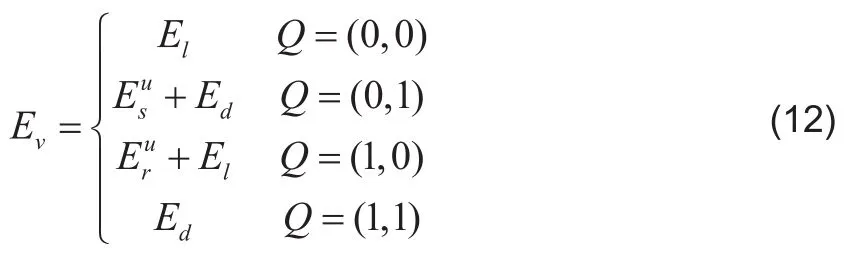
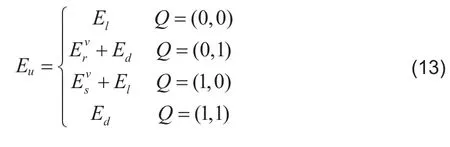
本文通過優(yōu)化任務調(diào)度的遷移策略來最小化執(zhí)行能耗，從而節(jié)約移動設備的能耗。

2 隨機任務遷移算法

本節(jié)提出一種基于貝葉斯網(wǎng)絡的任務遷移算法，根據(jù)子任務之間的依賴關系構造貝葉斯網(wǎng)，并求出最小化能耗的遷移策略。

2.1 貝葉斯網(wǎng)絡

貝葉斯網(wǎng)絡結合了圖論、概率論以及機器學習等理論和技術，是以有向無環(huán)圖的形式建模。用節(jié)點表示系統(tǒng)中的變量，用有向邊表示變量間的依賴關系。

貝葉斯網(wǎng)絡可以通過圖形化的方式對變量間的定量依賴關系進行描述，在聯(lián)合概率分布中給各個變量均賦予一個特定值于是利用貝葉斯網(wǎng)絡中的各個節(jié)點所對應的條件概率分布表，將所需的其他概率信息計算出來[8]。表示概率，則有：

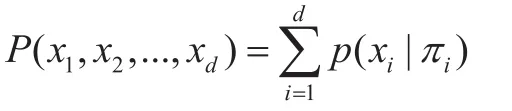
貝葉斯網(wǎng)絡中節(jié)點之間的依賴關系由條件概率函數(shù)決定。每一個沒有父節(jié)點的節(jié)點都有一個先驗概率分布。這些節(jié)點都具有各自的邊緣概率表，該邊緣概率表顯示相應節(jié)點獨立的概率分布。邊緣概率表中的概率數(shù)值表示了相應節(jié)點處于各個狀態(tài)的概率。每一個邊緣概率表中所有概率數(shù)值的和都為1。

每個具有父節(jié)點的節(jié)點都有相應的條件概率函數(shù)，該條件概率函數(shù)表示父節(jié)點和子節(jié)點之間的條件概率關系。兩個節(jié)點之間的條件概率關系由條件概率表表示。條件概率表為子節(jié)點變量在給定父節(jié)點變量情況下的概率情況。

當貝葉斯網(wǎng)絡建立后，通過一定的計算，可以獲得貝葉斯網(wǎng)絡內(nèi)變量之間的依賴關系以及變量的概率分布。由此，依據(jù)貝葉斯網(wǎng)絡中節(jié)點間的依賴關系以及變量的條件概率表，可以獲得聯(lián)合概率分布。此外，使用貝葉斯推理，可以利用已知的變量，通過貝葉斯網(wǎng)絡中節(jié)點間的連接，計算出其它未知變量的信息[8]。

2.2 基于貝葉斯網(wǎng)絡的遷移算法

根據(jù)應用的任務劃分圖構造一個貝葉斯網(wǎng)，每個子任務作為貝葉斯網(wǎng)的一個節(jié)點，根據(jù)子任務間的依賴關系構造貝葉斯網(wǎng)中各個節(jié)點之間的依賴關系。在貝葉斯網(wǎng)中可將不可遷移任務對可遷移任務的調(diào)度決策的影響轉換為依賴前置任務的本地執(zhí)行概率和依賴后置任務的本地執(zhí)行概率，即當某個子任務屬于不可遷移子任務，在對該子任務的前置子任務和后置子任務(均屬于可遷移子任務)做調(diào)度時，考慮后置任務的執(zhí)行位置是更有利于得出最優(yōu)調(diào)度策略的。

當任務v有前置任務u時，任務v和任務u的條件概率表分別如表1和表2所示。

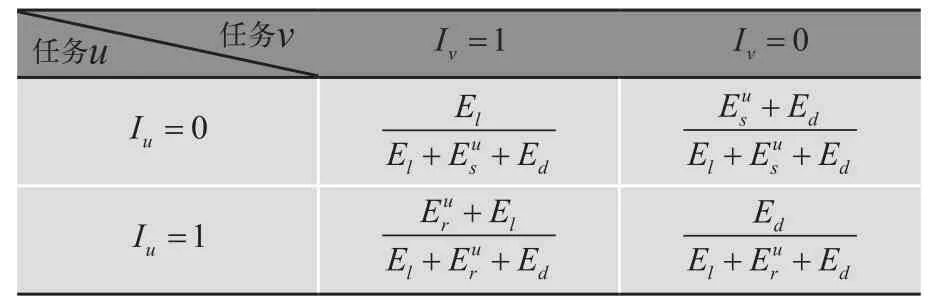
表1 任務的條件概率表

表2 任務的條件概率表

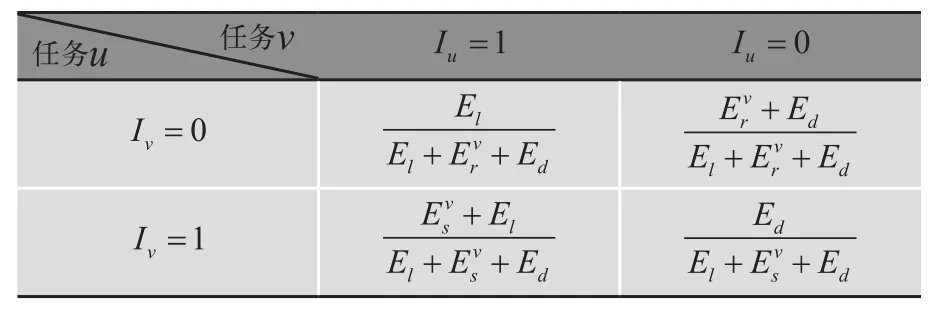
表2 任務的條件概率表

根據(jù)構造的貝葉斯網(wǎng)絡的依賴關系可以得出貝葉斯網(wǎng)的聯(lián)合概率：

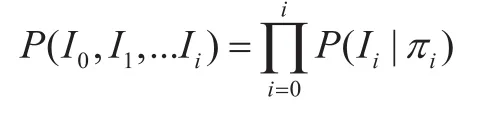
由于有的任務被設定為必須在本地移動設備上執(zhí)行的任務，所以圖2中的任務0、5可以表示為其他任務則利用聯(lián)合概率計算出每個任務在本地移動設備執(zhí)行的概率，以任務1為例，其依賴前置任務時在本地執(zhí)行的概率為：

利用動態(tài)規(guī)劃對上式進行化解得：

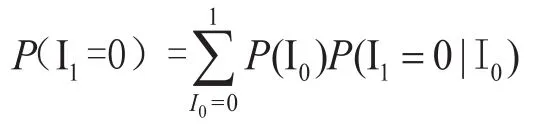
任務1依賴后置任務時在本地執(zhí)行的概率：

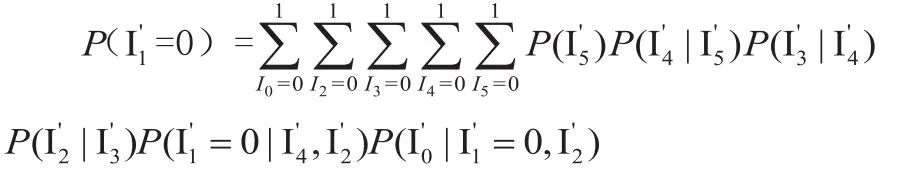
利用動態(tài)規(guī)劃對上式進行化解得：

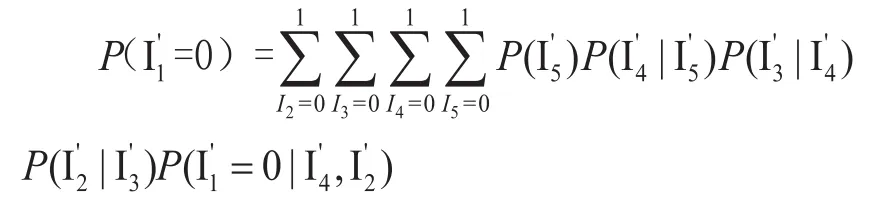
當獲得任務v在本地移動設備執(zhí)行的前置和后置概率后，若本地移動設備執(zhí)行的前置和后置概率之和大于MEC服務器執(zhí)行的前置和后置概率之和，則任務v在本地移動設備執(zhí)行，否則，則任務v遷移到MEC服務器執(zhí)行，計算式如下：

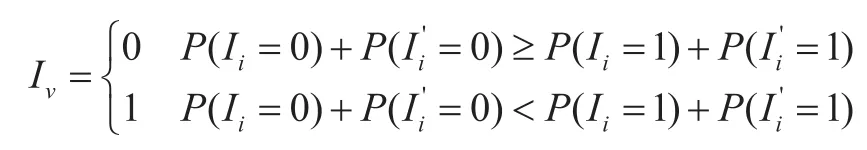
至此，可獲得一組次優(yōu)的遷移策略，然后對這組次優(yōu)遷移策略執(zhí)行一種弱窮舉算法，該弱窮舉算法認為每一個位置的狀態(tài)與其他位置的狀態(tài)是不相干的，在進行窮舉時，每次只改變某一個位置的狀態(tài)，并且在下一次窮舉時，上一次改變的狀態(tài)要恢復原樣。弱窮舉算法是為了解決原算法陷入局部最優(yōu)解的問題，通過改變每一個位置的狀態(tài)來跳出局部最優(yōu)解，并且弱窮舉算法具有低復雜度的特點，使得算法的能耗并沒有大幅增加。在本算法中執(zhí)行弱窮舉算法即依次在這組次優(yōu)遷移策略中選擇一個位置(該位置必須為可遷移任務所在位置)，將其替換為相反的遷移策略，再計算其總能耗，最后在所得的結果中選擇能耗最小的遷移策略為最終遷移策略。

根據(jù)上述的方法，對可遷移子任務逐個計算在本地移動設備執(zhí)行的概率，并依據(jù)前置依賴和后置概率決定任務的執(zhí)行位置，再通過弱窮舉算法得出一組最小化能耗的最優(yōu)遷移策略。在計算最優(yōu)遷移策略時，需要遍歷整個任務拓撲圖，其時間復雜度為而通過窮舉法遍歷整個解空間來找到最優(yōu)解，由于所有解的數(shù)量為個，故窮舉法的時間復雜度為貝葉斯遷移算法的時間復雜度是常數(shù)級別的，而窮舉法的時間復雜度卻是指數(shù)級的。由此得出，貝葉斯遷移算法的時間復雜度遠小于窮舉法，極大地減小了計算量。

3 仿真結果

在本節(jié)中，對提出的算法在python環(huán)境中進行了編碼實現(xiàn)并且通過仿真實驗對其性能進行了評估。仿真場景是：一個移動設備，一個搭載MEC服務器的基站，它們之間通過無線網(wǎng)絡連接。移動設備和MEC服務器參數(shù)如表3所示。

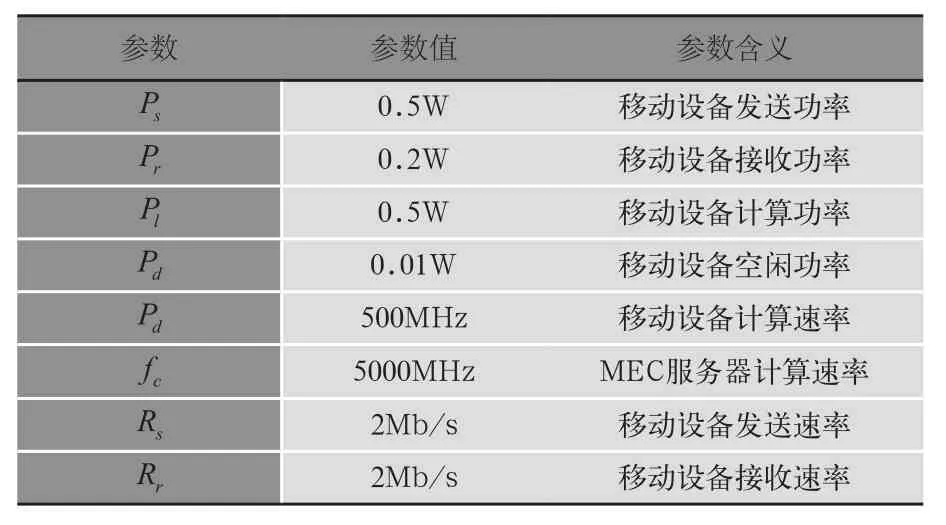
表3 移動設備和MEC服務器參數(shù)

為驗證算法的有效性，引入3種基本的任務調(diào)度算法作為對比，包括隨機任務隨機遷移算法、MEC服務器遷移算法和移動設備本地執(zhí)行算法[6]。與此同時，為驗證算法魯棒性，仿真中構建了10種不同的應用，這些應用的子任務數(shù)和子任務間的依賴關系均不相同，子任務構造如表4所示，并且任務子模塊數(shù)據(jù)大小和任務的負載量服從均勻分布，即根據(jù)應用的子任務劃分圖，將每個子任務作為貝葉斯網(wǎng)中的一個節(jié)點，按照子任務間的依賴關系構造貝葉斯網(wǎng)中節(jié)點間的依賴關系。

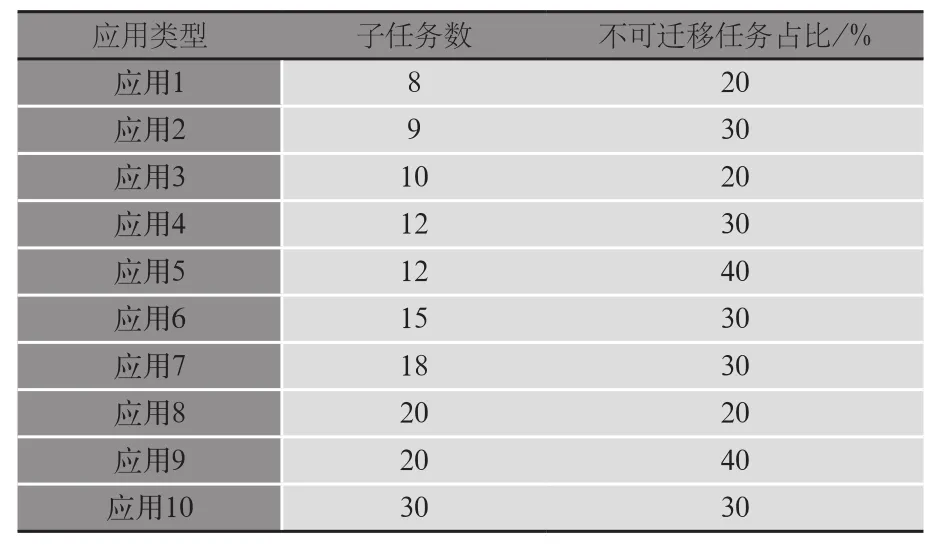
表4 應用子任務構造表

圖3展示了1000個任務在不同任務遷移策略下的能耗，從圖4中可以看到隨著任務數(shù)的增加，移動設備的能耗值呈線性增長，但是可以看到使用不同的遷移策略對能耗值的增加幅度的影響不同[10]。全部本地遷移策略由于其所有任務都在本地執(zhí)行，所以它的總能耗值是最高的。全部服務器遷移策略由于其所有可遷移任務都在服務器執(zhí)行，移動設備的能耗只有傳輸能耗，所以它的總能耗值小于全部本地遷移策略的總能耗值。隨機遷移策略由于其遷移決策是隨機的，對能耗產(chǎn)生的影響時好時壞，所以它的總能耗值介于全部本地遷移策略的能耗值和全部服務器遷移策略的能耗值之間。貝葉斯遷移策略所得出的遷移策略近似于最優(yōu)解，所以它的總能耗值是最小的。

圖4展示了1000個任務在貝葉斯遷移策略和窮舉策略下的能耗，從圖4中可以觀察到在不同任務數(shù)下，貝葉斯遷移策略和窮舉策略的能耗值是幾乎重疊的。這說明了貝葉斯遷移策略雖然沒有遍歷整個解空間，但是最終得到的最優(yōu)解和窮舉策略得到的最優(yōu)解基本一致，這也證明了貝葉斯遷移策略在降低時間復雜度的同時對能耗的優(yōu)化效果沒有損失。

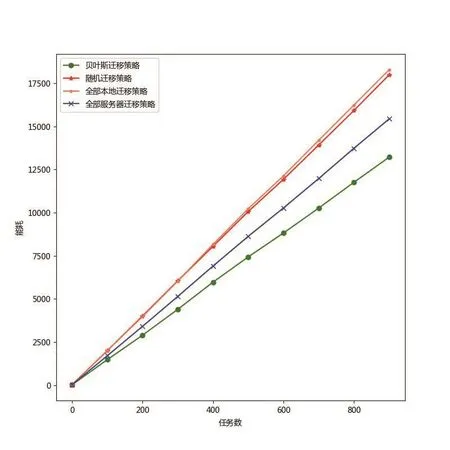
圖3 不同任務遷移策略能耗圖

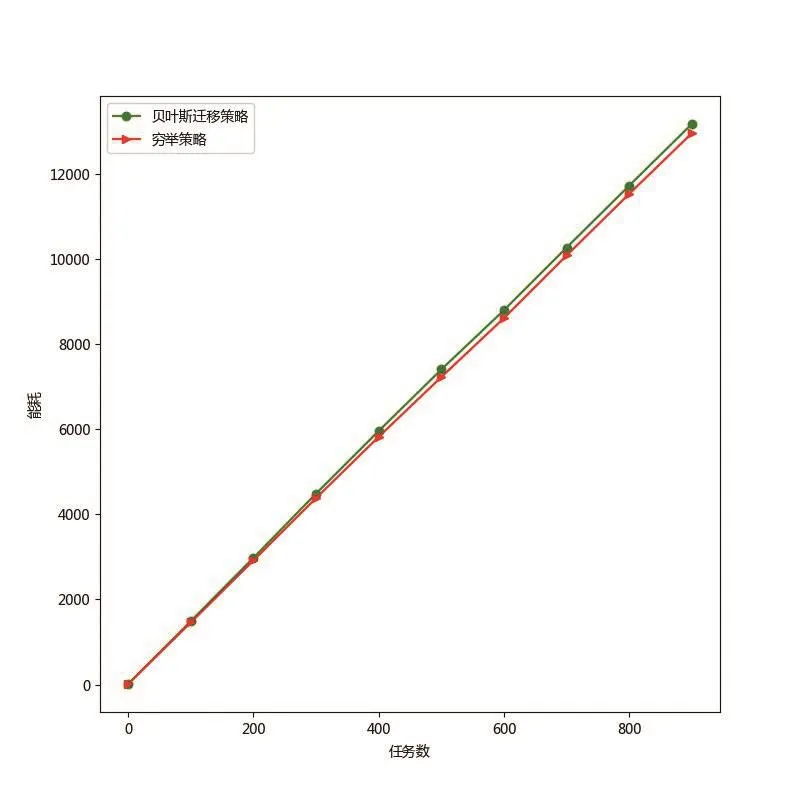
圖4 貝葉斯遷移策略和窮舉策略能耗圖

4 結語

本文提出了在單用戶MEC系統(tǒng)中基于貝葉斯網(wǎng)絡的隨機任務遷移算法，通過將應用轉換為包含多個子任務的有向圖，利用貝葉斯網(wǎng)絡中對子節(jié)點的概率計算方法來計算當前子任務遷移決策的先驗概率，然后根據(jù)概率以移動設備能耗最小化為優(yōu)化目標生成一組調(diào)度策略，最后利用弱窮舉算法對生成的調(diào)度策略進行調(diào)整來得出最佳的調(diào)度策略。該算法在一個隨機任務到達時能夠以常數(shù)級別的時間復雜度找到該任務的近似最優(yōu)解，提高了優(yōu)化效率。仿真結果表明，該算法對大量任務的遷移決策是非常有效的，使能耗得到了大幅度的減少。未來的研究工作主要包括加入對多任務能耗的優(yōu)化、對移動設備無線信道傳輸功率的控制等。