多區域大規模迭代計算框架應用研究

王曉斌 盧福軍 殷 穎 閆 萌 馬忠義

1 中國聯合網絡通信有限公司山西省分公司 太原 030006

2 山西建筑工程(集團)總公司 太原 030012

3 東北大學軟件學院 沈陽 110169

前言

在數學中，迭代函數是可重復與自身復合的函數，反復地運用同一函數計算，前一次計算得到的結果被用做下一次計算的輸入，這個過程叫做迭代。在計算機科學中，迭代是程序中對一組指令(或一定步驟)的重復，它通常描述一種特定形式的具有可變狀態的重復。迭代算法是用計算機解決問題的一種基本方法。它利用計算機運算速度快、適合做重復性操作的特點，讓計算機對一組指令(或一定步驟)進行重復執行，在每次執行這組指令(或這些步驟)時，都從變量的原值推出它的一個新值。即使是看上去很簡單的算法，在經過迭代之后也可能產生復雜的行為，衍生出困難問題的求解方法[1]。

隨著數據挖掘、機器學習等相關領域的發展，越來越多的迭代計算應用到諸如社會網絡分析、高性能計算、推薦系統、搜索引擎、模式識別等領域中[2]。例如：網頁排名算法PageRank算法根據網頁之間的鏈接關系進行迭代并收斂至最終結果，其迭代本質即從任意迭代初始點開始，根據迭代函數進行反復迭代更新；K-means算法反復迭代更新數據聚類中心點，根據最終收斂的不動點結果來判定數據單元的聚類所屬關系；協同過濾(Collaborative Filtering)算法，通常作用在用戶與購買商品關系的二維圖上，通過交叉運行以用戶為核心的和以商品為核心的兩個迭代計算過程，最終收斂的兩個向量表示購買習慣相似的用戶群和功能相似的商品群，利用相似用戶群中其他用戶的商品喜好信息來進行個性化推薦。

“海量”是大數據的一個主要特點。大數據是數據量龐大且分布廣泛的數據，當我們談及大數據時，很難假設數據是集中存儲的，也很難認為數據是靜態存儲的。眾所周知，大數據分析算法期望作用在全集數據而非局部數據之上，而“全集”又是相對的。因此迭代分析算法既會在各局部數據上執行，得到相對局部的分析結果；又會在匯總的全集數據上運行，產生相對整體的分析結果。我們對這種迭代稱為多區域大規模多級迭代計算，簡稱多區域迭代。多區域迭代計算原理如圖1所示，這是本文的研究重點。我們從文獻[2]中得到了大量的啟發，類似的工作包括Pramod等人提出了Incoop[3]框架，以及文獻[4]中，提出的針對PageRank算法的增量式迭代分析計算。

1 系統架構

在大數據環境背景下，基于Hadoop MapReduce[5]的HaLoop框架[6]是現階段相對成熟的分布式迭代計算框架，它采用MapReduce的編程模型使得其可以充分利用廉價的分布式服務器集群得到強大的迭代分析能力，并對Hadoop框架進行適應迭代分析算法的改進，從而支持大數據下大部分迭代分析算法的運行。近些年，由于計算機硬件的快速發展，UC Berkeley AMP Lab提出了Spark框架[7]。Spark框架與HaLoop框架不同，它完全作用于內存計算，而無需從HDFS上讀寫迭代數據，迭代的分析速度更快、更便捷，因此Spark框架能更好地適用于機器學習和數據挖掘等計算機科學領域中的迭代分析算法。綜上所述，多區域大規模迭代計算將選擇Spark計算框架作為計算平臺，通過對Spark框架的擴展實現大數據環境下的多區域迭代計算。

將迭代計算模型運用于山西聯通大數據業務分析領域，其系統架構如圖2所示。例如山西聯通組織機構可以根據地理位置劃分為太原分公司、大同分公司、呂梁分公司、臨汾分公司等11個地市分公司，每個行政地市都有對應的通信業務分析機構，對區內自身的通信數據進行分析操作，獲得區域內可靠的通信結果；而對于山西聯通省公司而言，也對應存在一個省級分析機構，用于全省數據的分析，即將各個地市的移動通信進行匯總，并在匯總后的全集數據上進行數據分析得到某市整體的分析結果。

在圖2中，藍色虛框標記的是區域(地市)分析機構的集群架構，包括各個地市自身的Spark&Yarn分析計算集群和存儲數據的分布式文件系統，紅色虛框標記的是省級分析機構的集群架構，主要由計算集群Spark&Yarn框架組成。各個地市基于內部的Spark&Yarn分析計算集群，在區內自身的數據上進行分析得到對應的區內分析結果，服務于區內個性化的政策和未來科學合理地決策，而當省級機構需要對全市數據進行分析時，各個地市的機構可以將自身區內的數據以及區內分析結果反饋給省級機構，省級機構可以基于省級的Spark&Yarn分析計算集群，直接在區內分析結果的基礎上進行迭代計算，快速地得到全省的分析結果。其中，各個區內(地市)的分析計算集群Spark&Yarn的架構如圖3所示。

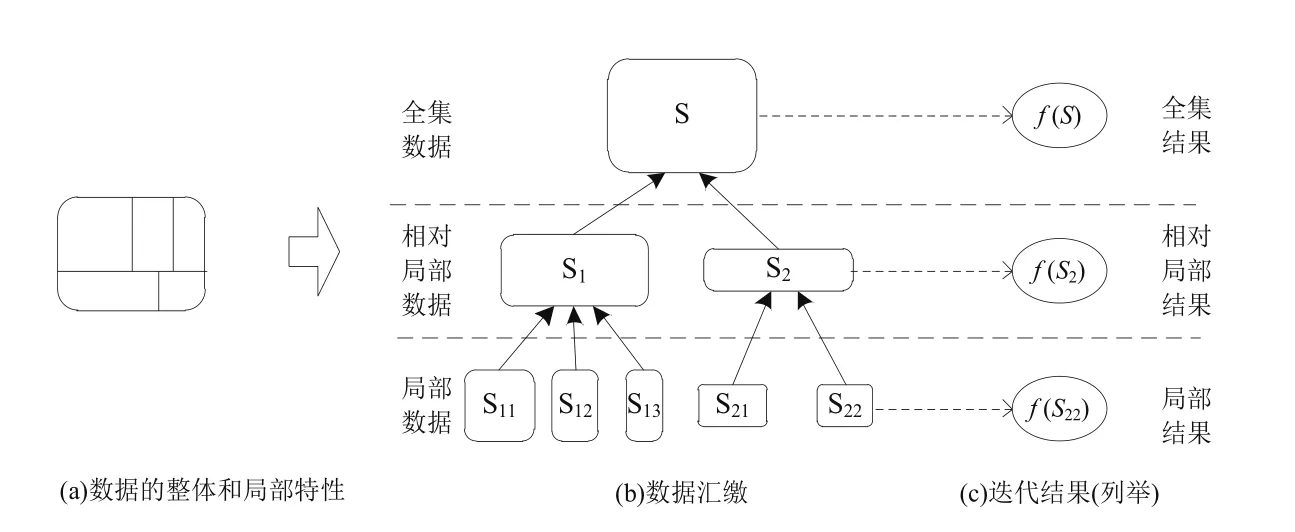
圖1 多區域迭代計算原理

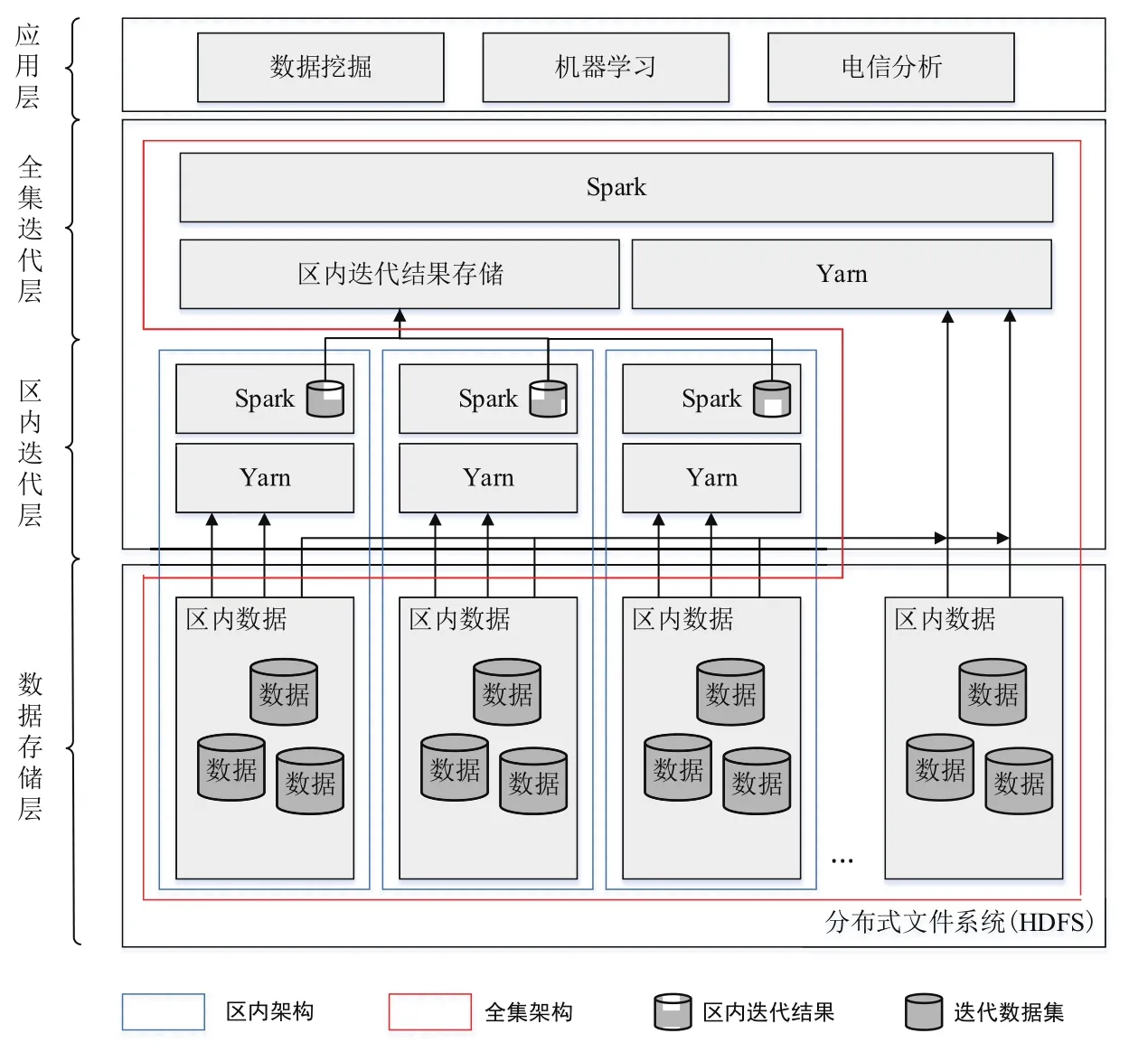
圖2 多區域大規模迭代計算系統架構圖

多區域大規模迭代計算框架的運行主要步驟為：Client提交迭代計算的應用，主節點構建迭代的運行環境并啟動Driver，Driver向主節點或者資源管理器申請迭代計算所需的資源，并通過SparkContext將迭代計算應用轉化為RDD Graph，再通過DAGScheduler將RDD Graph分解為Stage的有向無環圖，將TaskSet發送給TaskScheduler，最終由TaskScheduler發送Task給對應的Executor執行迭代任務。在迭代計算任務執行的過程中，Yarn中的Resource Manager負責迭代計算資源的分配和調度，其中Container是迭代計算資源分配和調度的基本單位，封裝了內存、CPU、網絡、磁盤等計算節點中重要的機器資源。

2 迭代算子

基于上節對多區域大規模迭代計算系統架構的介紹，我們可將框架主要分為以下幾個模塊：RDD(Resilient Distributed Datasets)算子模塊、迭代調度模塊、迭代計算模塊。其中最重要的為RDD算子模塊，是實現區域迭代的核心。

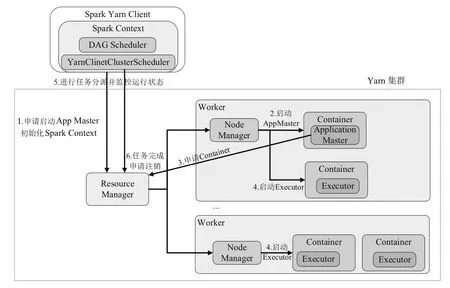
圖3 多區域大規模迭代計算框架Yarn模式的架構圖

RDD彈性分布式數據集，是迭代計算系統中的數據抽象，提供了一種高度受限的共享內存模型，即RDD是只讀的，分區記錄的集合。每個RDD數據集合都有以下屬性。①RDD之間的依賴關系：RDD在進行變換過程中，會由一個舊RDD變換為一個新RDD，兩個新舊RDD數據集之間存在類似流水線一樣的前后依賴關系，通過RDD之間前后的依賴關系，我們可以在某些分區數據丟失時進行恢復性計算，得到正確的迭代結果；②分片Partition：分片是RDD數據集的基本組成單元，針對每個RDD數據集而言，每個分片都會被指定一個迭代計算任務進行處理，并決定了迭代計算的并行粒度。于此同時，RDD還具有一個分片函數，用于對RDD數據集進行分片，包括基于哈希的分片函數HashPartitioner和基于范圍的分片函數RangePartitioner；③列表：用于存儲RDD數據集中每個分片的有限位置，在HDFS文件系統中，該列表存儲的是RDD數據集中每個分片所在塊的位置。通過該表對RDD數據集中各個分片位置的存儲，我們可以實現“移動數據不如移動計算”的思想，在迭代計算任務調度過程中，盡可能地將計算任務分配給將進行迭代計算所需資源所在的位置。

同時，RDD只能基于穩定物理存儲，并通過在其中的數據集合對其它已有的RDD執行確定性變換操作來創建。當RDD數據集創建完畢后，可以在RDD數據集上進行兩種數據操作，分別是①轉換Transformation：在現有RDD數據集的基礎上創建一個新的RDD數據集；②動作Action：在RDD數據集執行完迭代計算后，將迭代結果返回給Driver組件。

表1和表2分別列舉了迭代計算系統RDD算子模塊中重要的轉換操作和動作操作，其中partition(Dataset)、merge(otherDataset)、loss(lossDataset)為多區域大規模迭代計算系統新增的3個RDD算子轉換操作，分別用于多區域迭代計算過程中的數據分區、合并區內迭代計算結果、區內迭代計算結果的誤差。其中，多區域迭代計算的編程模型如下所示。

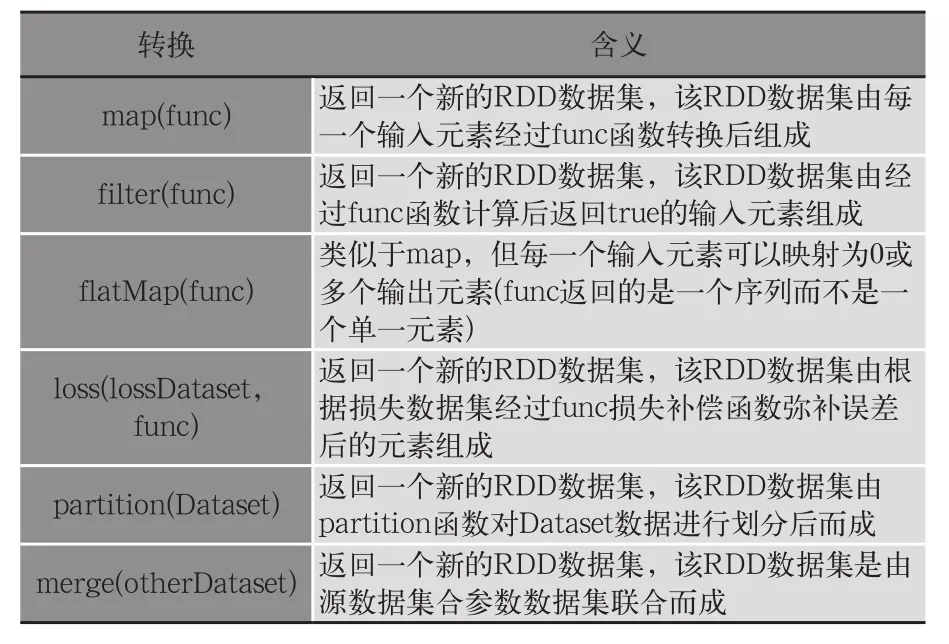
表1 RDD數據集的轉換操作表

表2 RDD數據集的動作操作表

3 實驗驗證

為了保證實驗結果的正確性和真實性，我們使用真實的物理計算機作為分布式集群進行實驗，其中包括1臺Master控制節點和12臺Slave計算節點。K-Means算法的測試數據集我們采用山西聯通真實的數據集。設多區域迭代計算模型中的迭代數據量為D，其中包含全集數據量以及區內數據量，同時區內數據量隨著全集數據量的增長而增長；區內迭代數據的分區記為P。K-means測試數據的相關信息如表3所示。

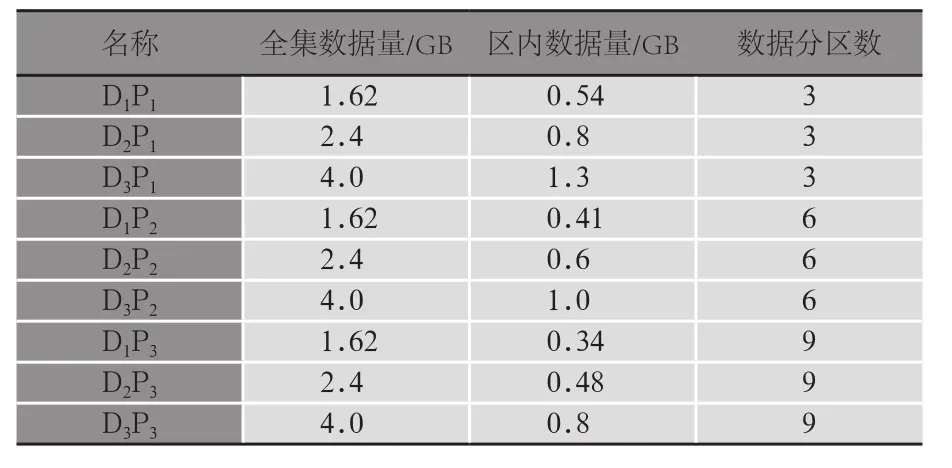
表3 K-Means測試數據集

全部實驗結果如表4所示，其中分別測量了多區域迭代與Spark迭代的迭代時長，并通過計算優化比例得出了多區域迭代的優化效果，優化比例的計算公式如下。

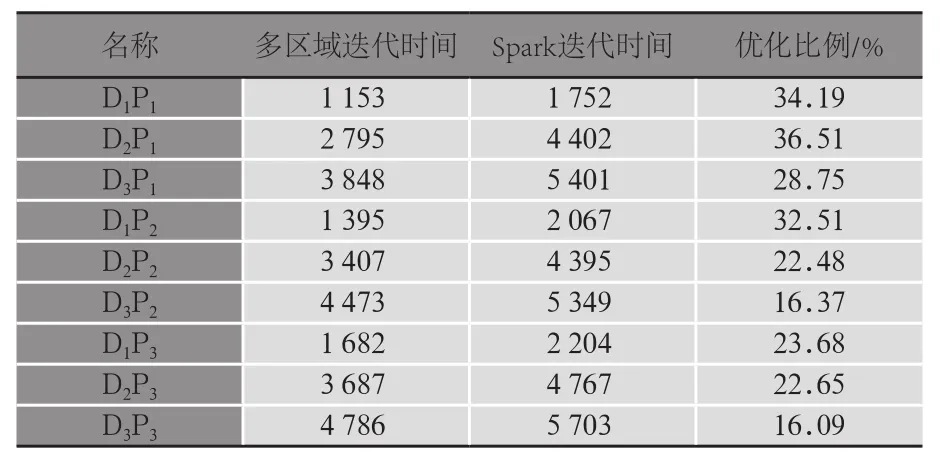
表4 實驗結果

圖4分別從不同數據量和不同分區數的角度展示了部分實驗結果。由于K-Means算法的迭代計算輪數對初始點的選擇非常敏感，為保證實驗結果的正確性，我們對每一組測試用例都運行了5次K-Means算法從而求取平均值進行分析比較。由圖4可知以下結論：①在各種條件下，多區域迭代計算框架的性能較傳統的Spark都有明顯的優化。優化比例最低也在15%至20%之間。②對于多區域迭代框架和Spark，數據量對于性能的影響大于分區數目的影響，其中數據量越大，或者分區數目越多，迭代性能越差。③我們設計的多區域迭代計算框架在給定用例下較Spark有性能優勢。

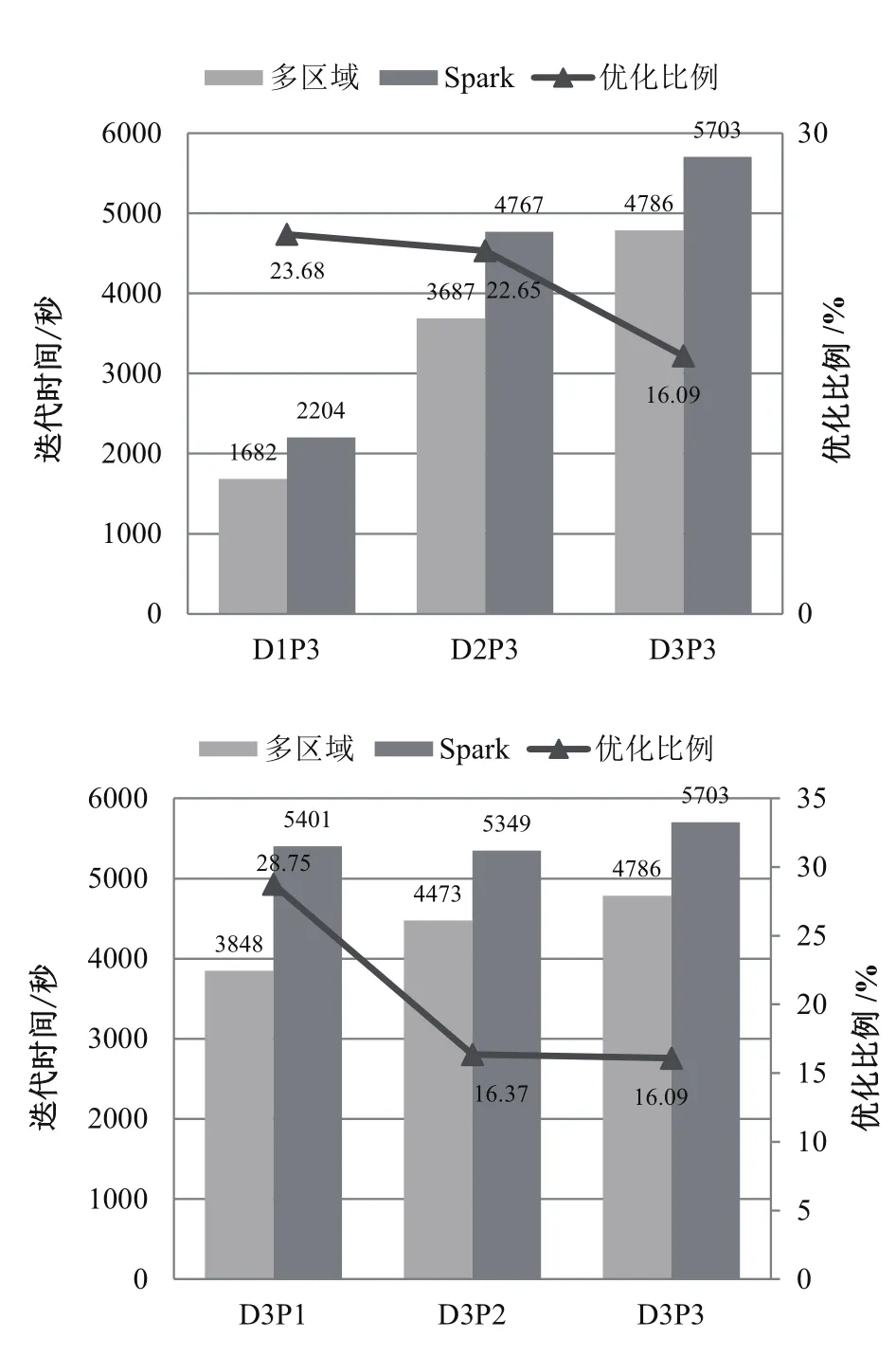
圖4 多區域迭代計算框架與Spark的性能對比

4 結論與展望

多區域大規模多級迭代計算的研究來源于中國聯通山西省分公司的具體數據匯集方式和分析需求，該研究成功提高了多地市數據分析和省級數據分析的效率，減少了省級數據分析的時間，減少了數據傳輸時延，有著確切的實際應用效果。然而，本研究仍處于初級階段，還有許多問題需要解決。首先，多區域迭代計算模型并非適用于所有的迭代算法，而且模型角度也不具有足夠的抽象性。其次，多區域迭代較全集迭代是有精度損失的，從實驗和實際證明該損失對于部分適用的迭代算法可以忽略不計，同時對損失的量化評估，還需要進一步研究。