單目視覺行人身體多部件距離融合估計算法

程 凡, 毛 琳, 楊大偉

(大連民族大學 機電工程學院，遼寧 大連 116605)

隨著智能汽車的快速發展，各種汽車輔助駕駛系統應運而生[1-2]，車前行人距離作為行人安全判斷的重要標準之一而受到廣泛關注。現今的距離估計系統大部分難以推廣，距離獲取速度較低，開發一種簡單易行的距離估計算法已經成為了刻不容緩的課題。

目前，應用于智能交通領域的行人距離估計方法通常采用微波測距、超聲波測距、激光測距、紅外測距和計算機視覺等。文獻[3]利用IR-UWB微波雷達系統進行測距，通過發射信號與回波信號的時間差對距離進行估計，但該算法耗時較長，算法穩定性較低；文獻[4]對原有超聲波測距算法進行了改進，提升超聲波頻率，擴大采樣范圍，并通過提升算法復雜度降低了對硬件的需求，但由于超聲波的傳播速度較慢，無法保證算法的實時性；文獻[5]使用激光測距系統與集光定位系統兩部分共同完成距離估計，系統距離估計結果精準，但對環境與使用設備要求高，難以廣泛推廣；文獻[6]中通過設置多個紅外發射接收器對距離進行估計，展現出了良好的實用性，造價低，反應速度快，但僅可應用于小范圍。機器視覺測距主要分為單目視覺測距與雙目視覺測距兩種方式。文獻[7]通過分析攝像頭內部參數并將參數分解為兩個線性方程組，以數學的方式對距離進行估計，降低了算法復雜度；文獻[8]將雙目立體視覺與紅外測距相融合，通過紅外測距法彌補了雙目立體視覺在距離估計范圍方面的不足。

本文提出一種基于單目視覺的行人身體多部件距離融合估計算法(M2DEA)，對圖像中的信息進行提取[9]，在僅以單目攝像頭作為圖像獲取設備的前提下，利用行人身體特征進行距離估計。本算法分別通過圖像中車前行人腳部件及頭部件像素高度估計距離，利用腳部件半水波形等距線及頭部件高度插值距離估計算法，融合兩種身體部件距離估計結果，避免了在復雜街道環境中行人身體部分被遮擋而無法實現距離估計的情況[10]，增強了算法的穩定性。

1 M2DEA算法

M2DEA算法以單目攝像頭作為圖像采集設備，利用不同身體部件特征進行車前行人距離估計，邏輯圖如圖1。圖像輸入后首先通過兩點法校正，建立圖像坐標系與世界坐標系的聯系，之后將校正后圖像作為輸入獲取行人的腳、頭部件，通過在線距離估計與離線模型標定兩部分，以線性最小方差為準則進行融合得到估計結果。

圖1 M2DEA算法邏輯圖

1.1 兩點法校正

攝像頭在固定時由于環境等因素難以保證角度水平，造成了世界坐標系與圖像坐標系轉換的偏差，通過兩點法對圖像進行校準。

在攝像頭位置固定后，垂直于地面且經過相機鏡頭光軸所在直線建立XOY平面，取一垂直于OY的直線L1L2；在L1L2上任取兩點D1、D2，D1、D2兩點應在攝像頭可視范圍內。標定場景示意圖如圖2。D1D2在實際場景中處于水平，故校準后兩點在圖像中仍應處于水平線上，通過角度偏轉、圖像平移兩步實現D1D2在圖像中的水平關系。

圖2 標定場景示意圖

采用兩點法對攝像頭獲取的圖像進行校準，建立了實際場景與圖像之間的聯系，通過對場景中對應點的標記實現世界坐標系與圖像坐標系的轉換，保證了后續算法對圖像深度信息挖掘的準確性。

1.2 半水波形等距線距離估計算法

半水波形等距線距離估計算法主要利用車前行人腳部像素位置作為特征對距離進行估計。根據多次實驗結果可以得出，行人腳部件位置與距離之間滿足一定的對應關系，且與攝像頭距離相同但位置不同的行人腳部像素位置呈水波形分布，故而提出半水波形等距線距離估計算法。經多場景仿真測試，車前行人腳部件像素坐標由相機擺放位置與行人距離共同決定，在道路平緩情況下，不受其他環境因素影響。故當相機擺放位置固定時，車前行人腳部件像素坐標將對應唯一距離，通過線下生成二者對應關系完成離線模型標定過程，在線完成實時距離估計。

半水波形等距線距離估計算法主要分為離線模型標定與在線距離估計兩部分。通過在實際場景中采集圖片，獲取行人腳部像素坐標與距離的對應關系完成離線模型標定過程。在離線模型標定過程中，需通過校正使得圖像坐標系符合世界坐標系準則。建立半水波形等距線模型，完成離線模型標定過程。在線距離估計中，通過能量濾波算法獲取待測圖像中行人腳部像素坐標，作為半水波形等距線距離估計法的輸入得到估計距離。

在離線模型標定過程中，以ri(i=1,2,3, ...,n)為等距線半徑得到采集點，采集點數量為n(n∈Z+)。采集工作在圖像左側完成，等距線關于x=0.5·lx對稱，lx為圖像寬度，右側采集點通過左側點映射獲取。通過曲線擬合建立ri條等距線。擬合曲線如圖3。

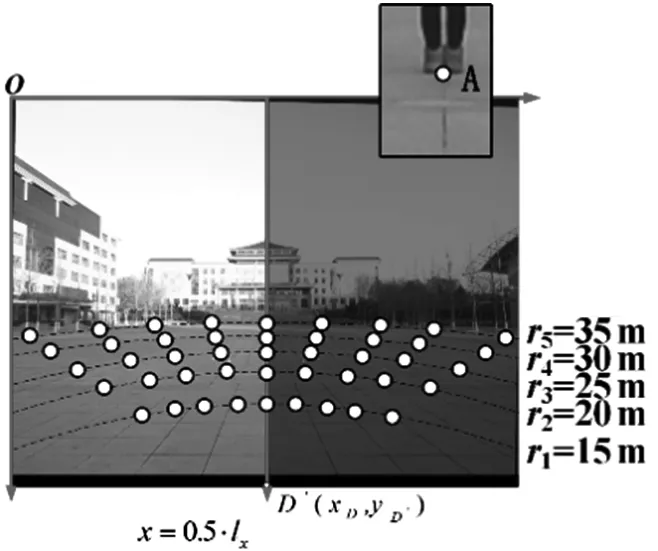
圖3 半水波形等距線模型

曲線擬合方法采用最小二乘法，等距線方程為

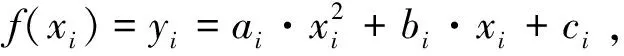
i=1,2,3, ...,n。

(1)

式中：ai，bi和ci為曲線擬合系數；xi和yi為圖像。像素坐標系坐標位置。同時，存在一條過原點O和A點的一次直線函數：

yi=k·xi,i=1,2,3, ...,n。

(2)

將公式(1)和(2)聯立方程組，求出直線OA與全部等距線在第I象限的交點坐標：

(3)

(4)

行人腳部部件A點到原點O的像素距離點集為

(5)

對所得距離點集P中各元素應用公式(6)插值，得出相對應的一組行人目標距離測量值d的對應關系。

1.3 頭部件高度插值距離估計算法

頭部件高度插值距離估計算法依靠頭部作為剛性部件的高度特征不變性對距離進行估計。算法主要分為離線模型標定與在線距離估計兩部分。通過實驗圖像獲取頭部像素高度與距離之間的對應關系，提出剛性部件尺寸-距離插值法，完成離線模型標定過程。在線距離估計中，通過超像素分割算法對圖像進行處理，獲得頭部像素高度后，經剛性部件尺寸-距離插值法獲取距離估計結果。頭部像素高度與距離對應關系如圖4，橫軸為頭部的像素高度，縱軸為行人目標與攝像頭之間的相對距離。

圖4 頭部件像素高度與相對距離關系

頭部像素高度與相對距離之間存在對應關系，故對距離的獲取主要依賴于行人頭部高度。在街道場景中，由于背景過于復雜，行人頭部高度難以獲取，為解決該問題，本文采用超像素分割算法[11]來完成目標行人頭部與背景的區分。首先通過DPM模型[12]檢測行人并劃分出頭部區域，超像素算法僅針對頭部區域內圖像進行處理，在去除頭部冗余像素的同時避免了實時性低的問題。頭部件高度獲取示意圖如圖5。

圖5 頭部件高度獲取示意圖

以O為端點任取一條射線OZ，并在該射線取n個標定點，令行人目標站在標定點上，對n個行人目標通過超像素算法對頭部高度hn進行計算，利用Lagrange插值求取頭部高度-距離的關系。設n個頭部高度插值節點為p，相對應的一組行人目標距離的地標點測量值d，頭部高度和距離的對應關系即為求一個插值多項式H，滿足

(6)

1.4 多部件融合算法

本文并行處理相對獨立的頭部件與腳部件進行距離估計，兩種算法互相校驗保證了算法的可靠性。同時，在人車混行的復雜環境中，身體部分部件極易被遮擋，通過不同身體部件進行距離估計，降低了算法失效的可能性。算法通過線性最小方差融合準則進行，只需計算加權系數，減小了計算負擔。

融合算法具體實施步驟如下：

(1)獲取距離估計結果。利用半水波形等距線距離估計算法及頭部件高度插值距離估計算法分別對同一位置上的行人進行距離估計，獲取兩組等精度距離估計值。

(2)獲取標準差。利用等精度數據判斷兩種方法的穩定程度，得出具體的標準差。由于單次測量精度相同，故其標準差均為σ。

(3)獲取權重。為保證算法穩定性，融合權重系數主要以標準差為依據進行判斷。給定基于頭部與腳部的測距算法所占權重分別為p1、p2，則各組算術平均值的標準差為

(7)

(4)獲取融合距離估計值。通過融合算法得出距離估計值D，頭部部件距離DH，腳部部件距離DF。

D=p1DH+p2DF。

(8)

2 仿真分析

仿真實驗在Matlab R2014a和Windows 7操作系統下進行。圖像以單目攝像頭作為圖像采集設備，鏡頭中心與地面距離為1.4 m，符合大多數車輛車載攝像頭高度，仿真在目標行人距離攝像頭5～35 m范圍內完成。仿真在非遮擋條件與半遮擋條件兩種情況下進行，當身體部件被半遮擋時，可通過未被遮擋單一部件進行距離估計。

2.1 非遮擋條件下仿真

累積誤差曲線如圖6，橫坐標為測量距離，縱坐標為累積誤差。融合后累積誤差低于單一算法的累積誤差值，該融合算法在距離估計準確程度上優于單一算法。

表1 身體多部件融合距離估計算法仿真結果

圖6 累積誤差曲線

仿真場景1、2在街道中進行拍攝的結果如圖7。令五名目標行人分別采取在路邊玩手機、面向攝像頭行走、橫穿斑馬線及橫穿車前的姿態。仿真場景2中令四名目標行人采取面向車輛行走、從障礙物后走出、橫穿車輛前及背離車輛行走的姿態。

2.2 半遮擋條件下仿真

在半遮擋情況下，采集路障后與行車路中間兩個場景對單一行人進行距離估計。在第一個場景中，行人腳部被路障遮擋，在第二個場景中，行人頭部被障礙物遮擋。仿真結果表明，本文提出算法在行人身體被部分遮擋的情況下，仍能輸出目標行人與攝像頭之間的有效距離，確保本算法在智能汽車及行人危險預判等方面的應用。

(a)仿真場景1 (b)仿真場景2

圖8 身體部件遮擋后距離估計

3 結 論

針對人車混行復雜環境中，自主汽車輔助駕駛系統對車前行人距離估計的問題，提出了單目視覺的行人身體多部件距離融合估計算法。依據行人身體特征進行距離估計，分別通過腳、頭部件構建半水波形等距線距離估計模型及剛性部件尺寸-距離插值模型。經仿真驗證，本算法距離估計結果在35 m距離估計范圍中，誤差在1 m以內。同時，在行人身體被半遮擋的情況下能夠對行人進行有效的距離估計，在35 m范圍內，可將誤差控制在2 m以內。本算法能夠為行人危險判斷提供有效的數據支撐，在智能汽車、無人車等研究領域中具有較強的應用價值。