基于信號配時的公交優先策略觸發概率模型
黃海南,李曉峰,連培昆,榮 建
(1.北京工業大學 城市交通學院,北京 100022; 2.福建農林大學 交通與土木工程學院,福州 350002;3.亞利桑那大學 土木工程與工程力學系,亞利桑那州 圖森 85719, 美國)(*通信作者電子郵箱hhnan021@foxmail.com)
0 引言
公共交通服務水平受限于公交車輛頻繁晚點運行、交叉口等待時間過長、高峰時段運力不足等關鍵問題,限制了公共交通的健康發展[1]。為了提高車輛準點率,很多城市在交叉口采用公交優先控制方法,減少公交車輛通過交叉口的等待時間,保證車輛運行效率[2-4]。
目前研究多集中在信號優先控制優化模型和算法,對信號機的優化控制邏輯和參數優化設置等方面的細化研究相對較少。文獻[5]中建立了基于被動優先的公交信號周期優化模型;文獻[6]中結合被動優先和主動優先策略進行干線協調控制;文獻[7]中提出無條件優先策略能使公交車輛行程時間縮短25%,但增加了公交車輛發車頻率較低的相交道路的車輛延誤;文獻[8]中基于邏輯規則的控制方法研究,增加公交信號優先控制策略的多樣性;文獻[9-11]中分別對主動優先控制邏輯作了相應改進;文獻[12]中研究了基于提前檢測器和到達時間窗的公交優先控制算法;文獻[13]中提出一種基于再勵學習思想以及智能體的有條件公交信號實時優先控制算法;文獻[14]中研究了鋸齒形公交專用道的預信號與主信號協調及延誤計算方法;文獻[15]在此基礎上研究了公交預信號控制與設計的結合問題。
現有信號機的公交優先控制邏輯無法響應公交車輛的累積到達數,控制參數的敏感性較低,針對這些問題,本文以西門子2070信號機為載體,在分析信號機公交優先觸發原理的基礎上,建立了公交優先策略觸發概率模型;利用公交優先硬件在環仿真識別,設計了多個對比的公交優先信號配時方案,運用觸發概率模型進行計算與分析,為公交優先控制參數與控制邏輯的優化提供理論支持。
1 信號機觸發原理
目前城市道路信號機以西門子信號機和海信信號機為主,相對于海信信號機單一的公交優先策略(紅燈早斷策略),西門子信號機的優先策略由優先相位的綠燈延長策略和非優先相位的紅燈早斷策略組成。為了同時測試兩種優先策略的觸發概率,測試設備選取了西門子2070信號機。由于不同類型信號機公交優先策略觸發機理并沒有差別,因此本文提出的觸發概率模型適用于使用相同公交優先策略的各類信號機。西門子2070信號機公交信號優先配時方案如圖1所示。
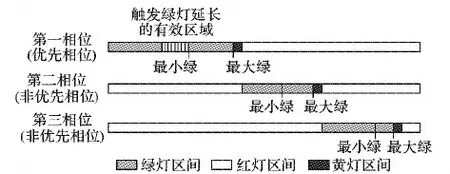
圖1 西門子2070信號機的公交信號優先配時示意圖Fig. 1 Schematic diagram of TSP signal timing on Siemens 2070 signal controller
信號機公交優先策略的觸發有三個關鍵的控制參數:1)最大呼叫時間Max_call,即公交信號優先呼叫保持激活狀態并有效的時間;2)延長時間Extend,即每個公交信號優先驅動(呼叫持續)從驅動終止點開始延長的時間;3)持續時間Duration,即公交信號優先要求的、在返回到正常的交通信號燈操作之前的時間。控制參數將影響不同相位綠燈時間,為協調交叉口各方向通行權,在控制系統中會設置最小綠燈時間Min_green保障該相位基本通行權利,同時設置最大綠燈時間Max_green限制該相位最長綠燈長度(見圖2)。
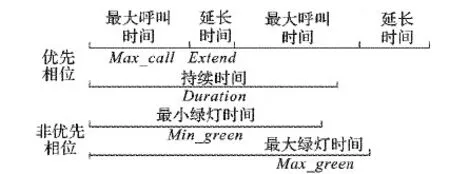
圖2 西門子2070信號機的公交信號優先配時參數簡圖Fig. 2 Parameter schematic diagram of TSP signal timing on Siemens 2070 signal controller
對于優先相位,如果沒有執行綠燈延長策略,最終綠燈時間為該相位的最小綠燈時間。只有在“觸發綠燈延長的有效區域”接收到公交優先申請,信號機才會執行延長一個Duration時長,最終綠燈時間才會大于其最小綠燈時間,即觸發綠燈延長策略。而在Extend范圍內接收到公交優先申請,優先相位并不會延長一個Duration時長。
對于非優先相位,如果沒有執行紅燈早斷策略,最終綠燈時間為該相位的最大綠燈時間。只要有任何一個非優先相位接收到公交優先申請,則觸發紅燈早斷策略。如果在最小綠燈時間與最大綠燈時間之間接收到公交優先申請,則該相位即刻結束,即該相位的最終綠燈時間為該相位的當前已運行時間。
2 優先策略觸發概率模型
2.1 綠燈延長策略的觸發概率模型
根據其觸發原理,綠燈延長策略最終表現為實際綠燈時長大于Min_stgY(優先相位的最小綠燈時間),公交車在T1、T2和T3這三種時長范圍內觸發公交信號優先均會導致綠燈延長,因此分別對這三種時長(式(1)~(3))進行概率計算(式(4)~(6))。
T1=Min_stgY-Max_Call
(1)
T2=Min_stgY-(Duration-Extend)
(2)
T3=Min_stgY-Duration
(3)

n≤Max_call(4)
P2(n)=
n≤Duration-Extend
(5)

n≤Duration
(6)
其中:n為優先相位接收到的總公交優先申請的數量;Pi(n)為不同前提條件下的綠燈延長觸發概率。
針對不同觸發前提條件,可計算相應綠燈延長策略的觸發概率(見表1)。
2.2 紅燈早斷策略的觸發概率模型
根據紅燈早斷策略觸發原理,分情景構建紅燈早斷策略的觸發概率模型。
1)情景1:總公交優先申請數量n=1。
Ai=Amberi-1+Redi-1+Max_stgi
(7)
其中:Ai為當前前提下,第i個非優先相位接收公交優先申請的作用范圍(i為當前非優先相位的編號,取值范圍為[1,k]);Amberi-1為前一相位的黃燈時間;Redi-1為前一相位的全紅時間;Max_stgi為當前非優先相位的最大綠燈時間。
第i個非優先相位紅燈早斷策略觸發概率P(i)由式(8)計算所得:
(8)
2)情景2:總公交優先申請數量n≥2且第1個非優先相位的公交優先申請數量m≥2。
第i個非優先相位接收公交優先申請的作用范圍Bi由式(9)計算所得:
Bi=Amberi-1+Redi-1+Min_stgi
(9)
其中:Min_stgi為當前非優先相位的最小綠燈時間。

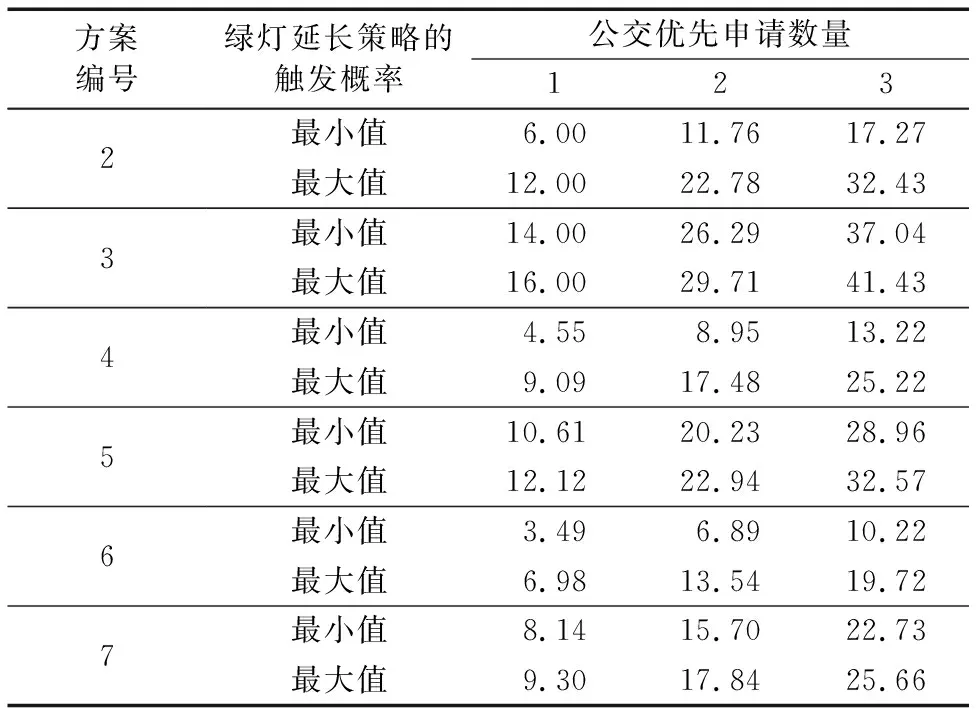
表1 綠燈延長策略的觸發概率統計表Tab. 1 Trigger probability statistics of green extension strategy
兩優先相位之間的所有非優先相位接收公交優先申請的作用范圍Dk,由式(10)計算所得:
Dk=B1+B2+…+Bk
(10)
除了第1個與第i個非優先相位外,兩優先相位之間的其他非優先相位接收公交優先申請的作用范圍Ei,由式(11)計算所得:
(11)
第i個非優先相位接收m個公交優先申請的組合數量S(i,m)由式(12)計算所得,該值的設定前提為第1個非優先相位的公交優先申請數量m≥2。
(12)
3)情景3:總公交優先申請數量n≥2且第1個非優先相位的公交優先申請數量m≥1。
除第1個非優先相位外,兩優先相位之間的其余非優先相位只能在最小綠燈時間范圍內接收公交優先申請。而對于第1個非優先相位,控制單元可在最大綠燈時間范圍內接收公交優先申請。該情景S(i,m)由式(13)計算。
(13)
4)情景4:總公交優先申請數量n≥2且第1個非優先相位的公交優先申請數量m=0。
當第1個非優先相位的m=0時,下一個非優先相位可在最大綠燈時間范圍內接收公交優先申請。如果下一非優先相位接收到公交優先申請,則其余的非優先相位只能在最小綠燈時間范圍內接收公交優先申請。以此類推,可推算前j個非優先相位均沒有接收到公交優先申請。前j個非優先相位接收公交優先申請的作用范圍Fj由式(14)計算所得。
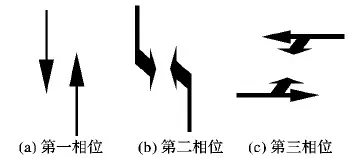
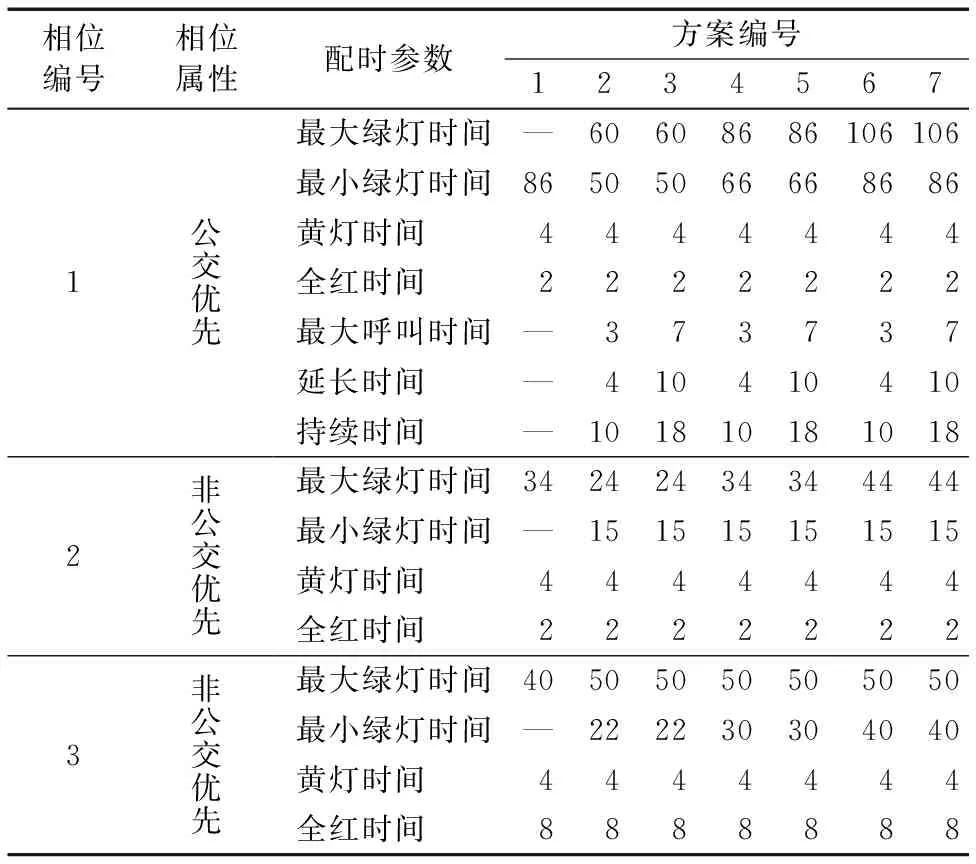
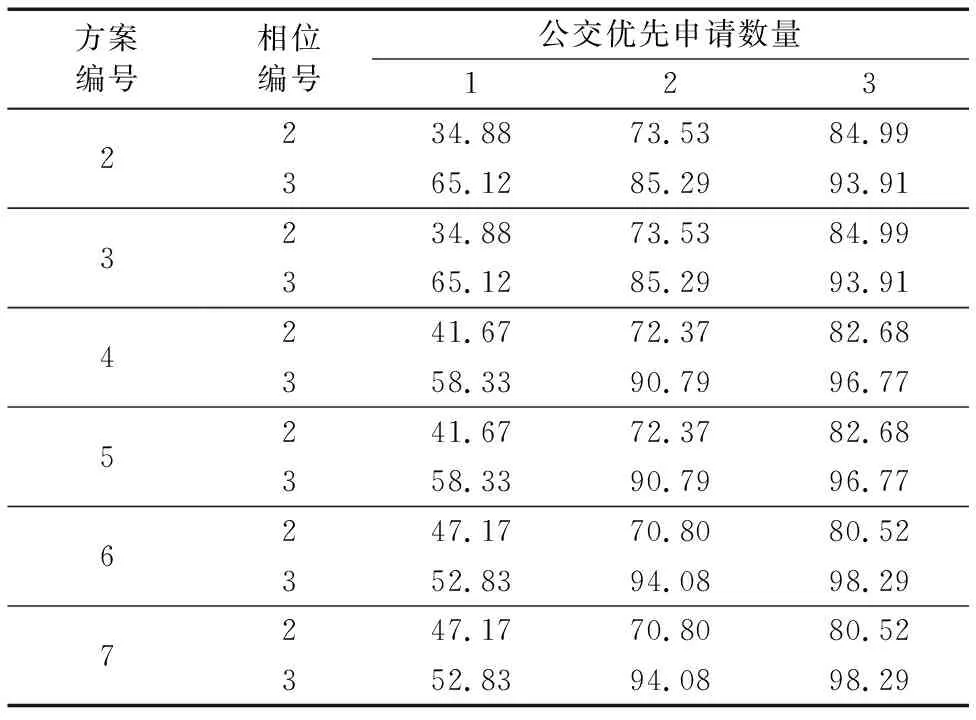
Fj=A1+A2+L+Aj;j (14) 除目標相位i外,第j+2個相位至第k個相位之間的非優先相位接收公交優先申請的作用范圍Gj由式(15)計算所得。 Gj=Bj+2+Bj+3+…+Bk-Bi;j (15) 在前j個非優先相位沒有接收到任何公交優先申請的情形下,第i個非優先相位接收m個公交優先申請的組合數量W(i,m,j)由式(16)計算所得。在第1個非優先相位沒有接收到任何公交優先申請的情況下,第i個非優先相位接收m個公交優先申請的組合數量W(i,m)由式(17)計算。 (16) W(i,m)=W(i,m,1)+W(i,m,2)+…+W(i,m,j); j (17) 綜上所述,當總公交優先申請數量n≥2時,第i個非優先相位有接收到公交優先申請的組合數量U(i,n)可由式(18)計算,則當控制單元在兩優先相位之間總共接收到n個公交優先申請時,第i個非優先相位紅燈早斷策略的觸發概率由式(19)計算。 U(i,n)=(S(i,1)+W(i,1))+(S(i,2)+ W(i,2))+…+(S(i,n)+W(i,n)) (18) P(i,n)=U(i,n)/[U(i,n)+U(i,0)];i (19) 選取北京市南苑路—久敬莊路交叉口為研究對象,其信號相位如圖3所示,第一相位為南北向直行相位,第二相位南北向左轉相位,第三相位為東西向直左相位,其中第一相位為公交優先相位,另外兩個相位為非公交優先相位。在晚高峰17:00—19:00信號配時方案的基礎上,設計7組公交優先信號配時方案(表2)并利用公交優先硬件在環仿真[16]進行觸發概率計算。其中:方案1為晚高峰時段的現場固定信號配時方案,包含3個主要參數;方案2~7為公交優先信號配時方案,相對于方案1增加了6個主要參數。為了測試不同因素對觸發概率的影響,提高方案間的對比性,設計了不同的方案參數,形成多個對比組。具體設置如下: 1)為了驗證固定信號配時參數對公交優先觸發概率的影響,設置方案2、3為短周期長度組,方案4、5為中周期長度組,方案6、7為長周期長度組。 2)為了驗證公交信號優先配時參數對公交優先觸發概率的影響,針對綠燈延長策略:方案2、4、6與方案3、5、7分別設置了相同的最大呼叫時間、延長時間及持續時間;方案2、3的最大綠燈時間與最小綠燈時間的差值為10 s;方案4~7的最大綠燈時間與最小綠燈時間的差值為20 s。針對紅燈早斷策略:方案2、3、4與6設置了非優先相位相同的最小綠燈時間;方案4與方案5,方案6與方案7分別設置了非優先相位相同的最大綠燈時間。 圖3 南苑路—久敬莊路交叉口信號相位Fig.3 Signal phase at the intersection of Nanyuan Road and Jiujingzhuang Road 表2 信號配時方案參數表sTab.2 Parameter table of signal timing plan s 3.2.1 綠燈延長策略的觸發概率分析 第一相位綠燈延長策略的觸發概率分布見表3。計算結果表明:1)最小綠燈時間越長,綠燈延長策略的最小觸發概率則越小,因而對最小綠燈時間進行優化可提高綠燈延長策略的最小觸發概率;2)最大綠燈時間越長,綠燈延長策略的最大觸發概率則越小,因而對最大綠燈時間進行優化可提高綠燈延長策略的最大觸發概率。由此可知,先進行固定信號配時方案(編號1)優化,再進行公交信號優先優化可提高綠燈延長策略的觸發概率。 最大呼叫時間的數值越大,綠燈延長策略的最小觸發概率也越大,因而對最大呼叫時間參數進行優化可提高綠燈延長策略的最小觸發概率;持續時間與延長時間的差值越大,綠燈延長策略的最大觸發概率也越大,因而對延長時間與持續時間兩個參數進行優化可提高綠燈延長策略的最大觸發概率。 因此,在公交優先控制邏輯不變的前提下,對于綠燈延長策略,可通過優化控制綠燈延長策略的優先參數來提高觸發概率,也可以通過優化固定信號配時參數讓盡可能多的公交車輛集中在優先相位的時長范圍內到達,增加公交優先申請落在優先相位的數量,從而提高綠燈延長策略的觸發概率。 3.2.2 紅燈早斷策略的觸發概率分析 紅燈早斷策略的觸發概率計算結果見表4。計算結果表明:隨著公交優先申請數量的加大,紅燈早斷策略的觸發概率也隨之增大,且該表中的數值均遠高于第一相位綠燈延長策略的最小觸發概率與最大觸發概率。對于各非優先相位,紅燈早斷策略的觸發概率均較高。如果將計算區間放大到所有的非優先相位,則所有非優先相位的總觸發概率將為100%,由此可知,通過優化控制紅燈早斷策略的優先參數來提高觸發概率的途徑效果有限。因此,優化紅燈早斷策略的觸發概率得通過優化固定信號配時參數以增加公交優先申請落在非優先相位的數量,但該做法不利于提高公交車輛的運行效率。 表3 優先相位綠燈延長策略的觸發概率計算結果 %Tab. 3 Trigger probability result of green-extension strategy for priority phase % 表4 非優先相位紅燈早斷策略的觸發概率計算結果 %Tab. 4 Trigger probability result of early-green strategy for non-priority phase % 在公交優先控制邏輯分析的基礎上,本文提出了公交優先策略觸發概率模型,并以西門子2070信號機為載體,利用公交優先硬件在環仿真進行觸發概率計算與分析,探索公交優先策略參數及控制邏輯優化方法。紅燈早斷策略的觸發概率遠高于綠燈延長策略,但需從交叉口的整體運行效率出發進行控制參數調節;綠燈延長策略控制參數敏感性較低,最佳優化方法是通過優化固定信號配時參數讓盡可能多的公交車輛集中在優先相位的時長范圍內到達,增加公交優先申請落在優先相位的數量。本文未考慮信號機接受公交申請的概率及交叉口信號配時的相位目標,后續研究可分析這些因素對觸發概率的影響。3 案例仿真分析
3.1 信號配時方案設計
3.2 結果分析
4 結語

