國際油價與中美股價的相依關系研究
——基于不同行業數據的分析
余樂安,查 銳,賀凱健,湯 鈴
(1.北京化工大學經濟管理學院,北京 100029; 2.湖南科技大學商學院,湖南 湘潭 411201; 3.北京航空航天大學經濟管理學院,北京 100191)
1 引言
石油作為能源市場中的最重要的產品,長期以來對世界各國的經濟有著深刻的影響。隨著世界經濟的發展,石油市場的金融屬性日漸凸顯,石油市場與其他金融市場之間的聯系也逐漸加強,石油市場的價格波動往往會引起其他金融市場的波動。股票市場作為一個國家經濟狀況的晴雨表,能反映一個國家經濟發展的整體狀況,揭示經濟運行中的諸多問題,股票市場的價格波動往往受到諸多因素的影響。研究石油市場的價格與股票市場的價格之間的相依關系,有利于我們掌握這兩個市場價格之間的波動情況,同時可以利用相依關系來進行風險預測和風險管理。對這兩者之間相依關系的研究將對降低投資風險,穩定金融市場以及促進經濟發展有著積極的意義。
目前的研究中部分學者從行業的角度分析了石油價格與股票價格之間的關系,從國內的情況來看,大部分學者使用的是傳統的計量模型來進行實證研究。金洪飛和金犖[1]利用國際油價與中國14個行業股票價格數據,運用雙因子多元GARCH模型進行實證分析,研究結果表明國際油價對不同的行業的有著不同的影響。李紅霞和傅強[2]采用多因素的GARCH模型分析石油價格變動對來自中國28個不同行業公司的股票價格的影響,發現不同行業的股票價格對國際油價的變動有著不同的反應。郭名媛和王娜[3]利用四種傳統的計量模型結合六個工業行業的收益和國際原油價格數據,分析原油價格和股票收益之間的關系,實證結果表明國際油價與股票收益之間存在著非線性的關系。程安和常清[4]利用不同的計量方法分析了國際油價與中國石油類企業股價之間的長期動態關系,發現二者之間的關系較為微弱。
從國外的情況來看基于行業層面對油價與股價之間的關系進行的研究也受到了較多的關注。Elyasiani等[5]利用GARCH(1,1)模型分析石油價格的變化對美國13個不同產業的影響,發現13個產業中有9個產業的股票價格與油價存在著顯著的對稱的相關關系,同時還發現使用石油的產業受石油價格波動率的影響比受石油價格本身變化的影響更大。Sadorsky[6]利用多變量GARCH模型分析油價和清潔能源公司股價之間的限定性關系以及波動率之間的溢出效應,通過比較不同GARCH模型之間的效果,發現動態限定性相依關系模型能很好地擬合數據。Arouri等[7]利用向量自回歸和GARCH模型分析國際油價和歐洲及美國不同行業股票之間的波動率溢出情況,發現國際油價與行業股票之間存在著明顯的波動率溢出效應,在歐洲波動率溢出效益是單向的,但在美國存在雙向的波動率溢出。Degiannakis等[8]利用多元時變的相關關系模型分析歐洲10個國家不同行業股票和油價之間的動態相關關系,他們發現不同行業股票價格和油價之間的相關關系是變化的,并且這種相關關系還受到不同行業特點的影響。Hamma等[9]研究了國際油價與突尼斯股票市場中不同行業股票價格之間的溢出效應,認為國際油價與不同的行業股票價格之間存在著負向關系,并且油價對股票價格只是單向的溢出效應。以上研究在一定程度上對油價和股價之間的相依關系進行了研究,但多利用的是傳統的計量方法,在刻畫油價和行業股票價格之間非線性的相依關系上有一定的缺陷,同時現有的研究方法很少將相依關系運用到風險度量上。
在上述的研究中,多數采用的是傳統的計量模型,而在最近的研究中,vine copula模型被廣泛應用于不同市場的相依關系和相依結構的分析中。Zhang Bangzheng等[10]利用vine copula模型研究10個股票市場之間的關系,通過預測VaR和ES比較了C-vine copula、D-vine copula和R-vine copula三種模型的預測效果,他們認為三種不同的Vine copula模型具有不同的相依結構,D-vine copula有更好的表現。Zhang Dalu[11]利用vine copula-GARCH模型分析了11個歐洲國家股票市場在歐洲主權債務危機期間的相依關系,結果表明,vine copula模型在預測危機方面有著較好的表現。Joe等[12]利用vine copula模型分析了金融市場中的非對稱尾部相關性,提出vine copula可以更好地解決尾部相關性問題。Righi和Ceretta[13]利用巴西股票市場數據研究了C-vine copula和D-vine copula相依結構上的不同,認為在巴西股票市場中一些行業有非對稱的尾部相關性,因此應加強對這些行業的風險管理。Beatriz和Bello[14]等提出了一種對copula魯棒性估計的方法,并將其運用到對巴西股票市場的波動率預測中,通過與其他方法的比較,認為C-vine copula模型有更好的預測精度。Czado和Min[15]利用混合貝葉斯方法,馬爾可夫鏈蒙特卡羅模擬與D-vine copula方法估計澳大利亞電力市場的相依結構。Smith[16]用五個不同的電力市場去驗證vine copula模型的預測效果,研究表明vine copula模型是估計多元相依關系的一種新的方法。楊坤等[17]利用vine copula模型和極值理論對六個原油市場的風險進行了度量,認為vine copula模型能較好的度量尾部風險。Sukcharoen和Leatham[18]利用vine copula模型對煉油廠存在的對沖風險進行了度量,發現D-vine copula可以有效的降低風險。Bensa?da[19]利用制度轉換vine copula模型分析了歐洲債務危機在不同市場間的傳遞,認為vine copula模型能很好地度量非線性相依關系。韓超和嚴太華[20]利用五種匯率間的相依關系進行研究,同時構建投資組合,發現vine copula模型能很好地度量投資組合的風險。
但是從目前的國內外研究狀況來看,現存的研究雖然有不少從行業的層面考慮國際油價和股票價格之間的關系,但首先其所用到的模型都是傳統的計量模型,缺少對相依關系有很好度量效果的vine copula模型的使用。其次,目前的研究多數只是分析油價和股價之間的相關關系,沒有將二者之間的聯系運用到風險度量之中。最后,雖然國外的學者從行業層面比較了不同國家股票價格和油價之間的相依關系,但是目前的研究很少從行業層面對中美兩國股票價格和油價之間的相依關系進行討論。因此,本文將利用vine copula模型從行業的角度對中美兩國股價和國際油價之間的相依關系進行比較,比較兩國股價和油價的相依關系在行業上的差別,并將相依關系運用到風險管理之中,用來篩選和構建投資組合,同時通過相依關系的模擬來度量投資組合的風險。
2 模型構建
本節將介紹基于行業層面進行相依關系和相依結構分析所需要的相關模型。2.1小節介紹邊緣分布建模的GARCH(1,1)模型,2.2小節介紹R-vine copula模型。
2.1 邊緣分布GARCH(1,1)模型
在進行vine copula模型建模過程中,首先需要對每一個變量進行邊緣分布的建模。我們將利用Kolmogorov Smirnov(K-S)檢驗模型擬合的效果。在GARCH模型中,利用概率積分轉換使得出的標準殘差序列轉換成服從0到1上均勻分布。由于在本章中涉及到較多的變量,因此我們采用相對統一的GARCH(1,1)模型對邊緣分布建模。這樣做的考慮是在保證對數據的擬合效果的前提下可以節省尋找不同GARCH模型的進行匹配過程。在這一章中我們將采用GARCH(1,1)模型和偏t分布以及偏廣義誤差分布進行搭配,利用偏t分布以及偏廣義誤差分布對不同變量的標準化殘差進行擬合。具體的模型形式如下:
rt=μ+εt
(1)
(2)
εt~σtet
(3)
et~i.i.dskewedstudent-t(χ,η)orskewedged(χ,η)
(4)
其中,rt為收益率,σt為條件方差,εt為殘差,et為標準化殘差。
2.2 R-vine copula模型
Copula模型最早是由Sklar[21]提出的,這是一種連接函數,該模型將變量的聯合分布函數分為兩個不同的部分,一部分是一系列的邊緣分布函數,另一部分是一個copula函數,其主要被用來分析不同變量之間的相依關系。隨著copula模型被廣泛的運用到不同市場的相依關系分析中,其在相依關系分析上的優勢逐漸顯現。對于兩變量X1和X2的一般Copula模型可以由以下的形式來表示:
F(X1,X2)=C[F(X1),F(X2)]
(5)
其中,F(X1,X2)代表著聯合分布函數,C是copula連接函數,F(X1)、F(X2)分別表示兩個變量X1和X2的邊緣分布函數。對于邊緣密度函數f(x1,x2)而言,該模型又可以被分為copula函數c[f(x1),f(x2)]與邊緣密度函數f(x1)、f(x2)的乘積,如下所示:
f(x1,x2)=c[f(x1),f(x2)]·f(x1)f(x2)
(6)
然而,隨著變量維數的增加,copula模型難以被用到高維數據的分析中,為了解決這一問題,Joe[22]提出vine copula模型來拓展copula模型的運用范圍。Vine copula 模型將多變量之間的成對的相依關系通過特定的結構組織起來,以此降低維數。常見的兩種vine copula模型是C-vine copula和D-vine copula。隨著vine copula模型的發展,近些年來,部分學者提出了R-vine copula模型。這三種不同的vine copula模型的不同之處在于相依結構的不同;在C-vine copula模型之中,有某一個變量作為根節點,其他變量與根節點聯系;在D-vine copula模型中,變量之間按照順序依次聯系,兩兩相互連接;在R-vine copula模型中存在著不止一個根節點,其他變量與這些根節點聯系。R-vine copula模型可以看成是C-vine copula和D-vine copula模型的拓展,當變量的數目較多時,可以考慮利用R-vine copula來對相依關系進行建模。R-vine copula模型的具體形式如下:
(7)
在這里,Kj表示根節點的集合,k={a,b},Dk代表的是除去a,b剩下的變量的集合。在該公式中,多變量的聯合密度函數可以由一系列的聯合密度函數和copula函數得到,這樣通過vine copula模型可以得到變量之間的相依關系。在本文中我們將利用到油價和中美股票市場不同行業的數據,變量的數量增多,使用R-vine copula模型對于估計變量之間的相依關系和相依結構更為妥當。
2.3 vine copula-GARCH模型計算VaR
在險價值VaR是用來計算在給定的期限和置信水平下資產可能遭受到的最大損失。通常情況下VaR受到兩個方面的因素影響,一個是資產的持有期限n,另一個是置信水平1-α%。在本文中,VaR都被假設為負值,可以由下面的公式計算出來:
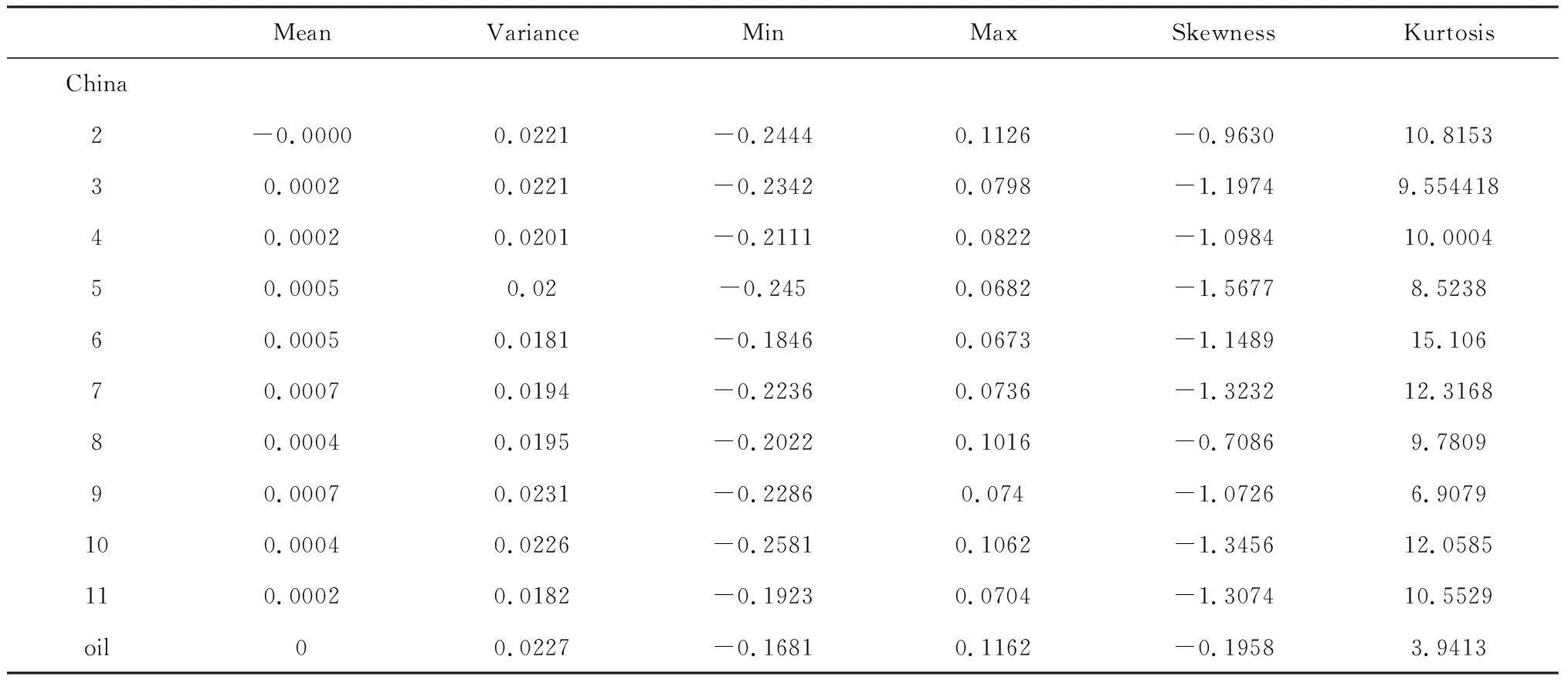
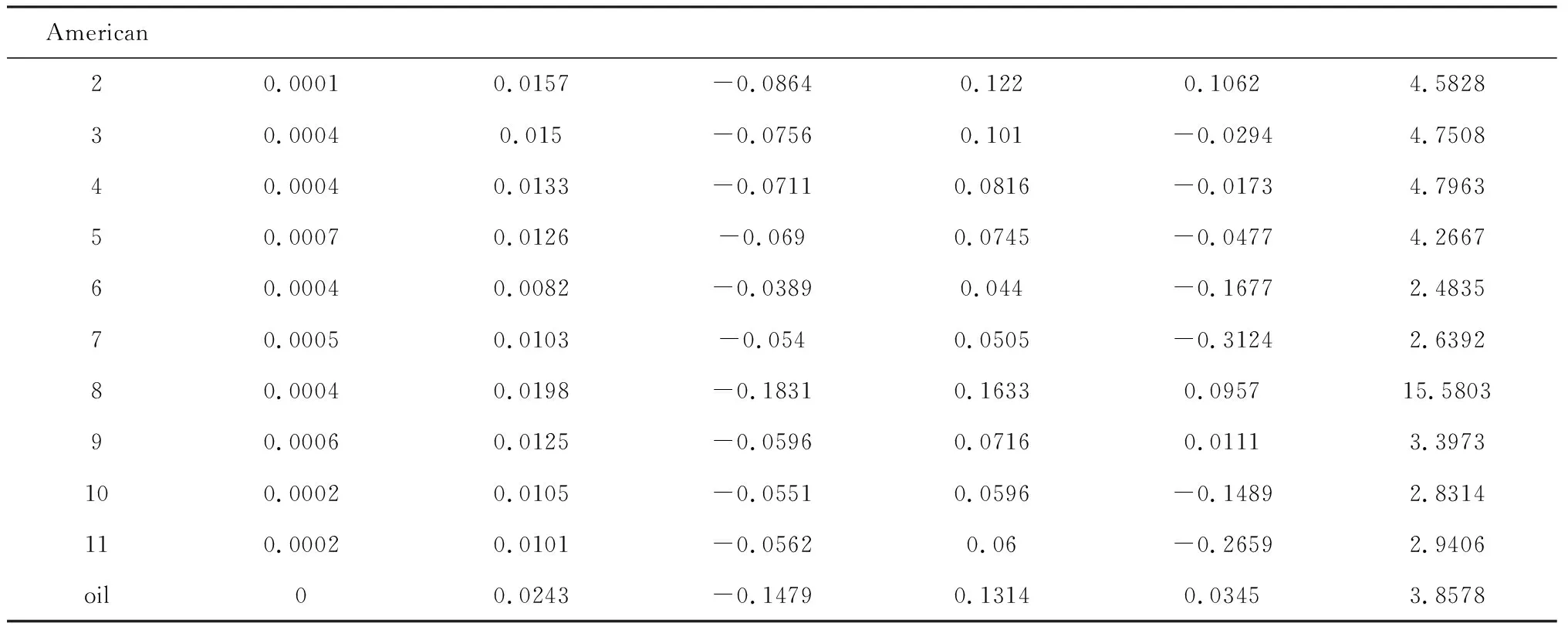
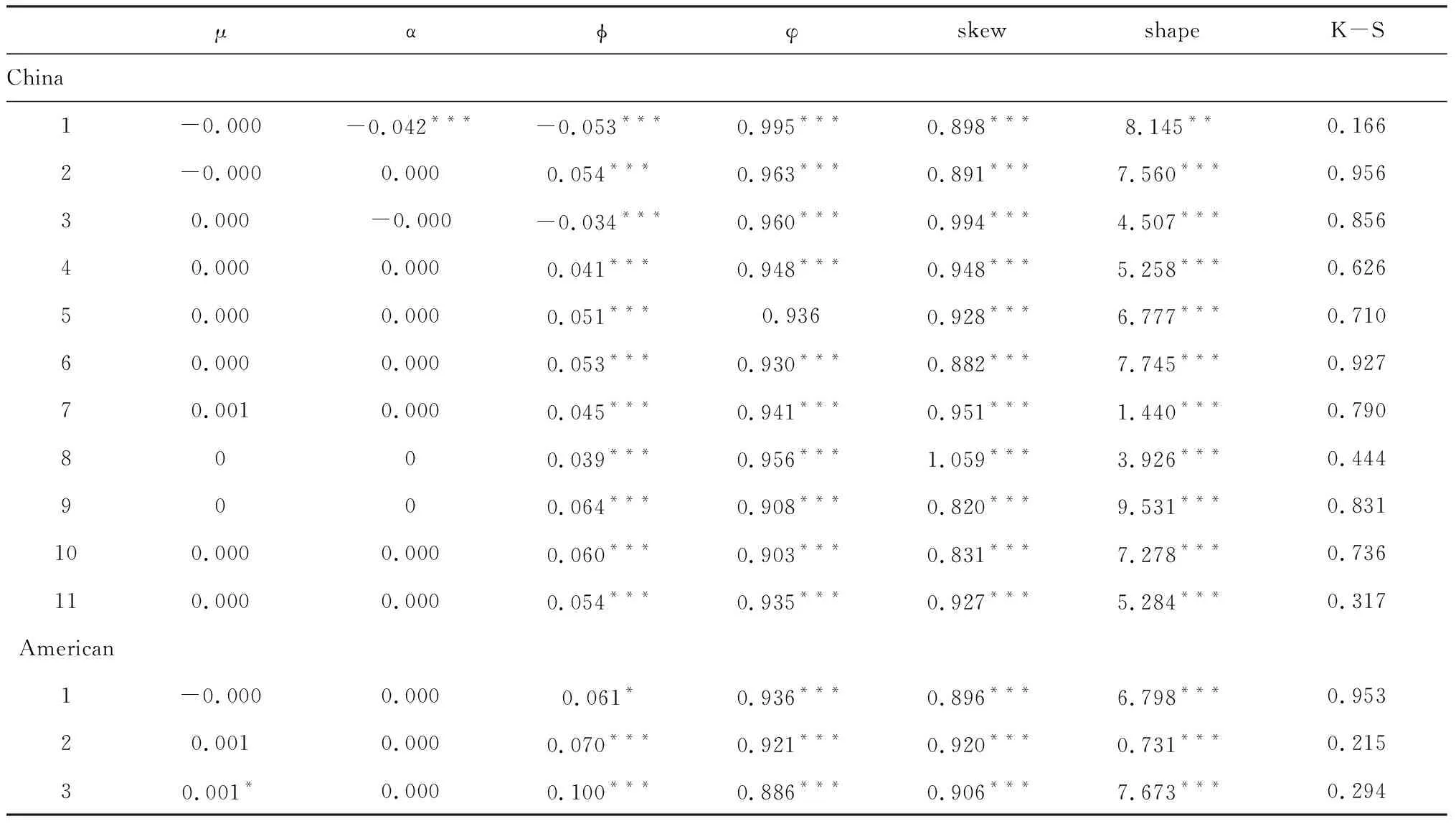
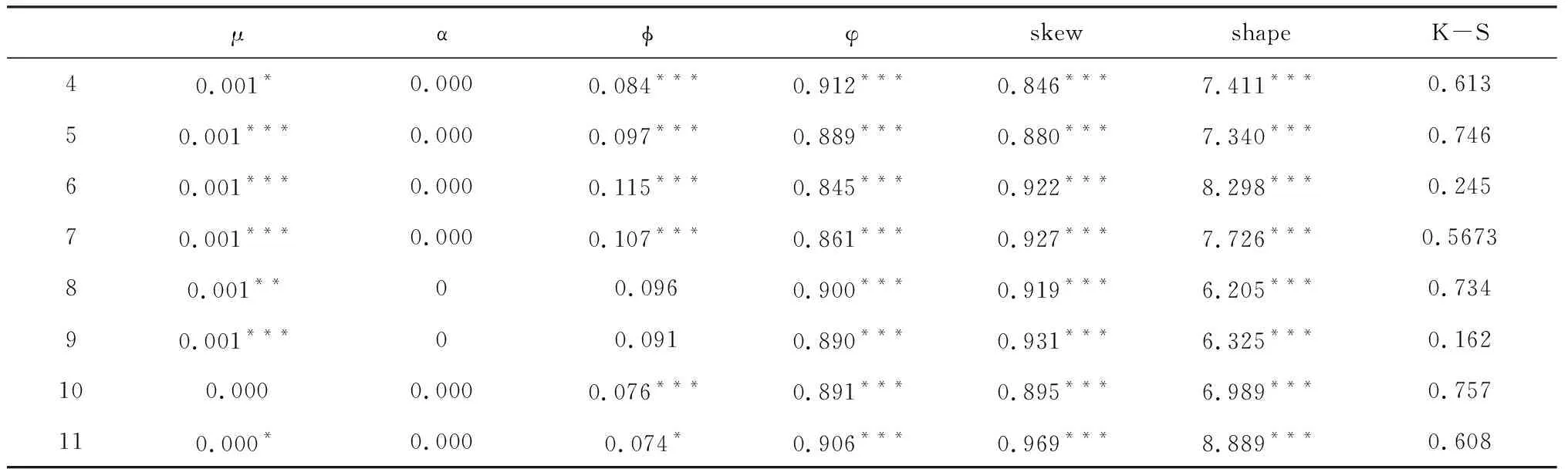
P(rn (8) 在這里rn是在持有期為n時的收益率。在本文中,投資組合由與油價相依關系最強的一個行業股票價格指數和油價構建,組合的收益率由二者的收益率等權重的加權平均得到。 傳統的計算VaR的方法主要有三種,分別是歷史模擬法、均值-方差法和蒙特卡洛模擬法 我們將利用vine copula模型以及GARCH模型來計算VaR,并將其與三種傳統方法進行比較。在vine copula-GARCH模型中,先利用GARCH模型對邊緣分布進行擬合,得出相關的參數;然后利用邊緣分布結合vine copula模型得出國際油價和中美股價之間的相依關系和相依結構;再次利用蒙特卡洛模擬計算出包含已知相依關系和相依結構的新的收益率序列,再利用新的收益率序列來計算VaR。最后,對vine copula-GARCH模型的預測效果進行回測檢驗。 vine copula-GARCH模型計算VaR的具體過程可以由以下幾個步驟來闡述: (1)GARCH模型將會被用來擬合不同的邊緣分布數據,通過這些數據得到GARCH模型的各個參數,以此獲得均值方差、條件方差方程和標準殘差序列。 (2)利用概率積分轉換,標準殘差序列將會被轉換成服從0,1均勻分布的copula數據,利用這些數據通過vine copula模型得到國際油價和中美股價之間的相依結構。 (3)模擬出下一天具有上述相同相依結構的copula數據,模擬5000次。將新的數據進行逆概率積分變換過程得到新的標準殘差數據。 (4)重復第三步n次,以此獲得未來n天的標準殘差數據,同時利用上述GARCH模型中的條件方差方程得到未來n天的條件方差。 (5)利用公式(9)計算出接下來n天的收益率,其中σi+n和φi+n分別是未來第n天的條件方差和模擬得到的標準殘差。通過這一步可以預測出未來n天的收益率數據。 ri+n=μ+σi+nφi+n (9) (6)運用等權重加權平均方法計算組合收益率,得到組合收益率,再利用公式(8)計算出VaR。 本節將利用國際油價和中美不同行業股票價格數據,分別對油價和中國行業股票以及油價和美國行業股票進行相依關系建模,得出他們之間的相依結構,最后選擇與油價相依關系最強的一個行業股票與油價構建投資組合,度量其風險,并與傳統模型進行比較。 本節將對WTI原油期貨價格數據和美國標準普爾十個行業股票價格數據以及中國上證十個行業價格數據進行分析。美國標準普爾的十個行業指數分別是能源,原材料,工業,非必需品消費,必需品消費,醫療,金融,信息技術,電信服務以及公共事業;中國上證的十個行業指數分別是能源,原材料,工業,可選消費品,主要消費品,醫藥,金融,信息技術,電信和公共事業。原油期貨數據來自于美國能源署,標準普爾十個行業指數來自于Wind數據庫,上證十個行業指數來自于國泰君安數據庫。選擇了從2009年1月9日到2016年11月15日的數據進行分析。選擇這樣一個時段的原因是該時段在金融危機之后,因此選擇在金融危機之后的這樣一個時間段來對油價與中美不同行業股價之間的相依關系進行分析,有利于分析金融危機給油價和股價帶來的影響。本文選擇了標準普爾指數而非道瓊斯指數,主要是因為標準普爾指數有對不同行業的分類,能夠獲取各個行業的指數數據,而道瓊斯指數更多的是反映股市的整體情況。 表1 描述性統計 續表1 描述性統計 表1展示了這些數據的描述性統計。在表中中國市場部分,從2到11分別對應的是能源,原材料,工業,可選消費品,主要消費品,醫藥,金融,信息技術,電信和公共事業行業指數;在美國股票市場部分從2到11分別對應的是能源,原材料,工業,非必需品消費,必需品消費,醫療,金融,信息技術,電信服務以及公共事業的股票指數。從表中的數據可以看到這些數據存在著不用程度的偏離標準分布的情況,因此我們在利用GARCH模型進行邊緣分布擬合時將采用有偏的t分布和有偏的廣義誤差分布來對殘差進行擬合。根據表2中K-S檢驗結果,其中除中國市場中的醫藥行業使用有偏的廣義誤差分布來擬合,其他行業均用t分布來擬合。 在上述的分析中我們已經強調在利用vine copula進行分析之前需要對每個變量進行邊緣分布建模。這一節我們利用統一的GARCH(1,1)模型來對油價和中美不同行業股票指數進行邊緣分布建模。建模得到的估計結果體現在表2中,表中的1表示的是油價。 表2 邊緣分布估計結果 續表2 邊緣分布估計結果 從表中可以看到,對標準化殘差進行K-S檢驗的結果在10%的置信水平下都能通過檢驗,說明擬合出來的數據可以用于vine copula模型的分析。 利用邊緣分布得到的數據對國際油價和中國上證十個行業股票指數以及國際油價和美國標準普爾十個行業指數進行相依關系的建模,得到的結果如表3所示。 表3 R-vine copula 估計結果 從R-vine copula 模型估計的結果中可以看到,國際油價和中國行業股價之間的相依關系與國際油價和美國行業股價之間的相依關系是不同的。首先,在相依關系的大小上,國際油價和中國行業股價之間的相依關系普遍較弱,即使是與油價相依關系最強的能源行業和信息技術行業,其與油價的相依關系也只有0.03和-0.03;而在美國股票市場中,能源行業與國際油價相依關系最強,達到了0.33,這與中國股票市場的情況相差巨大;導致出現這種狀況的原因在于中國國內的包括石油在內的能源價格多數是自主定價,國際市場的能源價格存在一定的脫節,使得國際油價與中國行業股指之間的相依關系較弱。其次,在與油價的相依關系中中美兩股也存在著行業之間的差別,中國與油價相依關系最強的兩個行業分別是能源和信息技術行業,而美國與油價相依關系最強的兩個行業是能源和工業;中國與油價相依關系最弱的是工業,在美國與油價相依關系最弱的是必需品消費。雖然兩個國能源行業都與油價的相依關系最強,但在相依關系的大小上存在著顯著的差異,在其他行業上,中美兩國也展現了一定的差異,將中美兩國行業對應起來,可以看到除了金融行業,美國的所有行業與油價的相依關系都要強于中國;這就說明了中美兩國在行業之間存在著一定的差異。造成這一差異的原因在意中國股票市場的開放程度不高,導致與國際市場之間的互動不夠。 在尾部的相依關系上,油價與中美兩國的行業股票之間也存在著較大的差異。在中國股票市場,行業股指與油價之間的尾部相依關系很弱,且多是非對稱的尾部相依關系,這就說明雖然在發生極端事件時,國際油價與中國行業股價的關系不強,但是會出現非對稱的風險。而在美國市場,國際油價與不同行業之間的尾部相依關系較強,且都是對稱的尾部相依關系,這就說明在發生極端事件時,美國的行業股價與油價之間的關系會較強。 通過上述分析,我們可以看到,國際油價與中美不同行業的股價之間的相依關系是不同的,總的來說,國際油價與美國行業股價之間的關系要強于國際油價與中國行業股價之間的相依關系;同時在尾部相依關系上,國際油價與美國行業股價表現出的是對稱的較強的相依關系,而國際油價與美國股價之間表現的是非對稱的較弱的相依關系。 在對國際油價與中美不同行業股價進行相依關系分析之后,我們將利用的vine copula-GARCH模型對油價和中美行業股價之間的投資組合進行風險度量。 我們選擇中美十個行業中與油價相依關系最強的行業組合成投資組合。對于美國而言,與油價相依關系最強的是能源行業,所以我們將美國能源行業的股票指數與國際油價組成投資組合;對于中國來說,雖然與國際油價相依關系最強的也是能源行業,但信息技術行業也和國際油價的相依關系在絕對值上與國際油價和能源行業的相依關系是相同的,所以我們將中國的能源行業指數和信息技術行業指數與國際油價組成投資組合。 表4和表5展示了對這兩個投資組合進行風險估計的結果以及回測檢驗結果。從風險估計的結果中我們可以看到,在對國際油價與美國能源行業的投資組合的VaR估計中,vine copula-GARCH模型展現出了較好的估計效果,在三個置信水平下都通過了回測檢驗;但在對國際油價與中國能源行業和信息技術行業的投資組合的VaR估計中,vine copula-GARCH的估計效果雖然要好于歷史模擬法和蒙特卡洛模擬法,但是估計效果要比均值-方差法,同時均值-方差法的估計效果雖然最好,但是在99%的置信水平下也沒能通過檢驗。出現這種情況的原因就在于國際油價和美國能源行業指數之間的相依關系較強,因而vine copula-GARCH模型的估計效果較好,而國際油價與中國行業指數之間的相依關系較弱,所以削弱了vine copula-GARCH模型的估計效果,相依關系的強弱會影響風險估計的結果。這一結果也提醒我們,利用相依關系較強的變量構建投資組合能提高風險估計的精度,有效地規避風險。 表4 VaR估計結果 表5 VaR回測結果 本文利用R-vine copula模型對中美不同行業股票價格指數和國際油價之間的相依關系進行建模,發現從行業的角度來看中美兩國的股價與國際油價的相依關系存在著顯著的不同,中國行業股價與國際油價之間的相依關系要弱于美國行業股價與國際油價的相依關系,雖然兩國的股票價格與國際油價相依關系最強的都是能源行業,但是相依關系的大小上存在著較大的差異,這種差異的原因在于國內能源價格與國際市場的脫節,因此應加強中國能源市場與國際能源市場之間的聯系,提高中國能源市場的價格對國際能源市場價變動的敏感度。同時通過利用相依關系的大小組成投資組合,對構成的兩組投資組合進行風險度量,風險度量的結果顯示出vine copula-GARCH對具有較強的相依關系的變量組成的投資組合能有很好的估計效果,變量之間的相依關系對投資組合的選擇以及對投資組合的風險預測至關重要。在未來的研究中可以利用相依關系來對投資組合進行選擇,以此降低投資過程中的風險。3 實證分析
3.1 數據描述
3.2 邊緣分布建模結果
3.3 R-vine copula模型結果分析
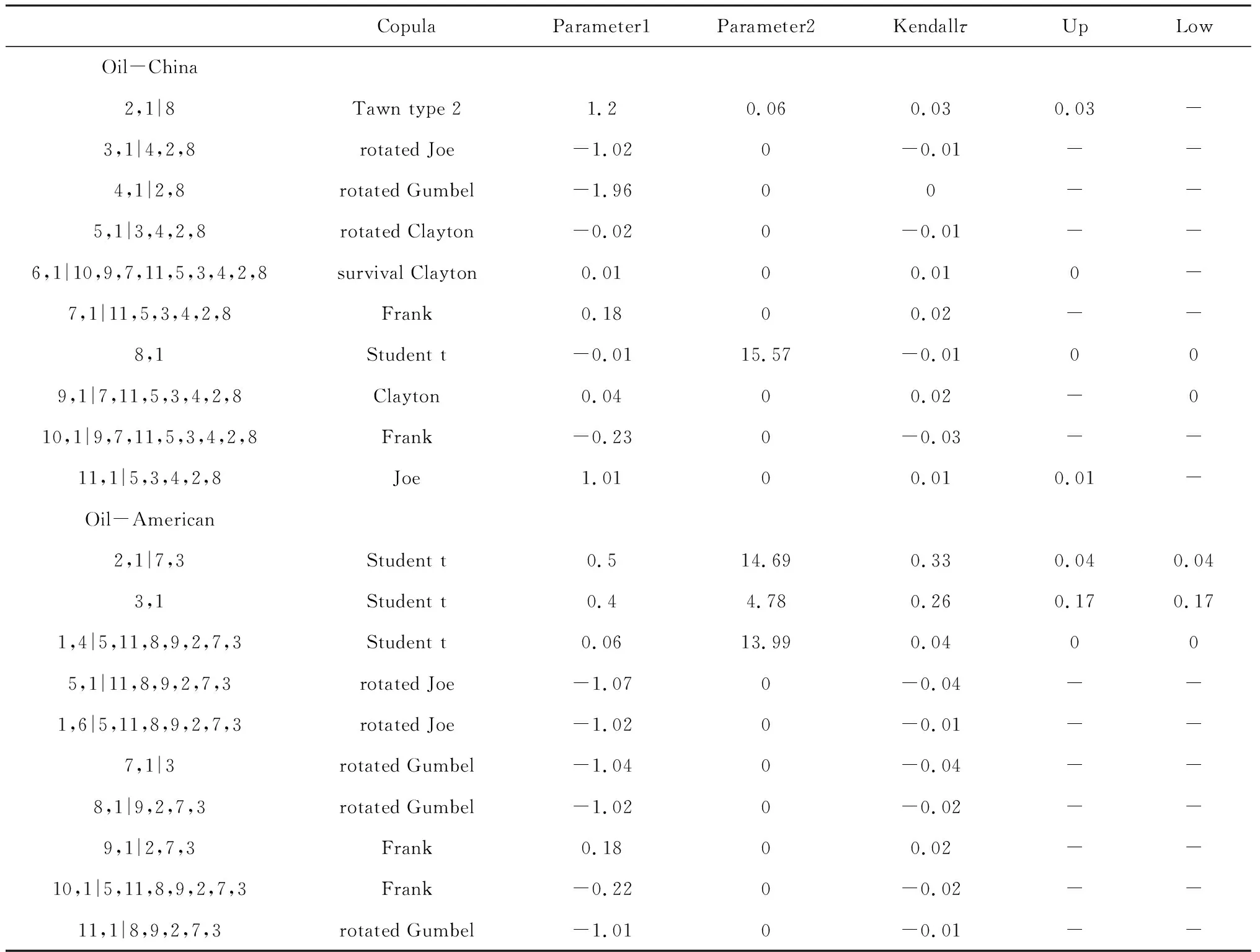
3.4 風險度量結果
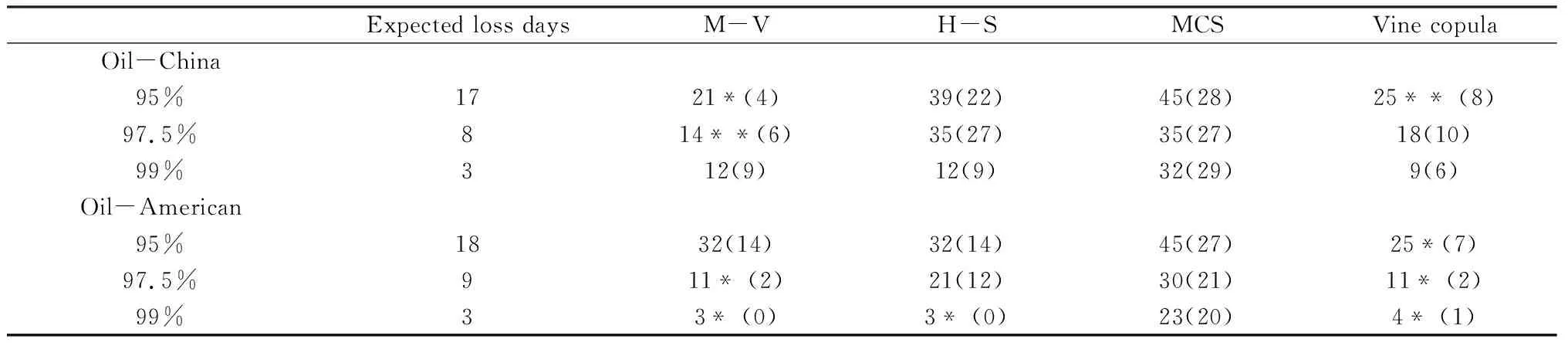
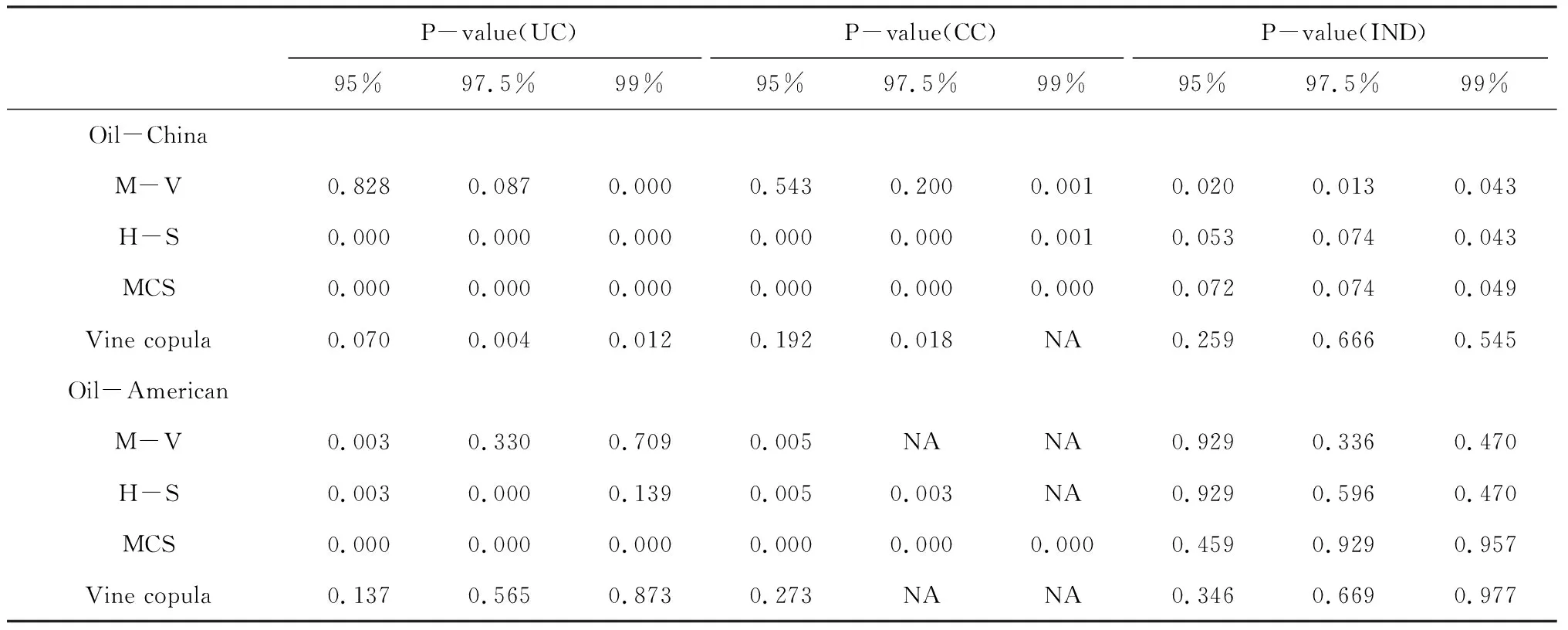
4 結語

