認識向量，親近向量

徐樹旺

向量是近代數學中重要和基本的數學概念之一，是溝通代數、幾何與三角函數的一種工具，有著極其豐富的實際背景，在數學和物理學科中具有廣泛的應用.向量內容已成為高中數學課程的“核心概念”之一.

一、向量體現了數學與物理的天然聯系

生活中的向量隨處可見：“風力3級，風向東北”、“飛機每小時向西北方向飛行900km”、“用了300kg的力向上提一物體”等，向量最初被應用于物理學，很多物理量如位移、速度、加速度、力等都是向量的原型，

如，兩接連的位移確定一個新位移——向量的加法（α十b）的原型（圖1）；力所做的功是由力與位移兩矢量（物理上矢量——既有大小、又有方向、又有作用點）唯一確定的一個數——向量的數量積（α·b）的原型（圖2）.

“向量”一詞來自力學、解析幾何中的有向線段，英國大科學家牛頓使用有向線段表示向量，將向量與力學應用結合在一起.笛卡兒坐標（x，y）形式的出現，使向量為力學應用提供了一種有效的數學工具.

二、向量代數“身份”的核心內容是運算

運算是數學學習中的一個基本內容，從小學開始，運算對象不斷擴展：從整數到分數、從正數到負數、從有理數到實數；從數到字母，再到多項式等；數運算、字母和多項式運算，這些都是數學中的基本運算.

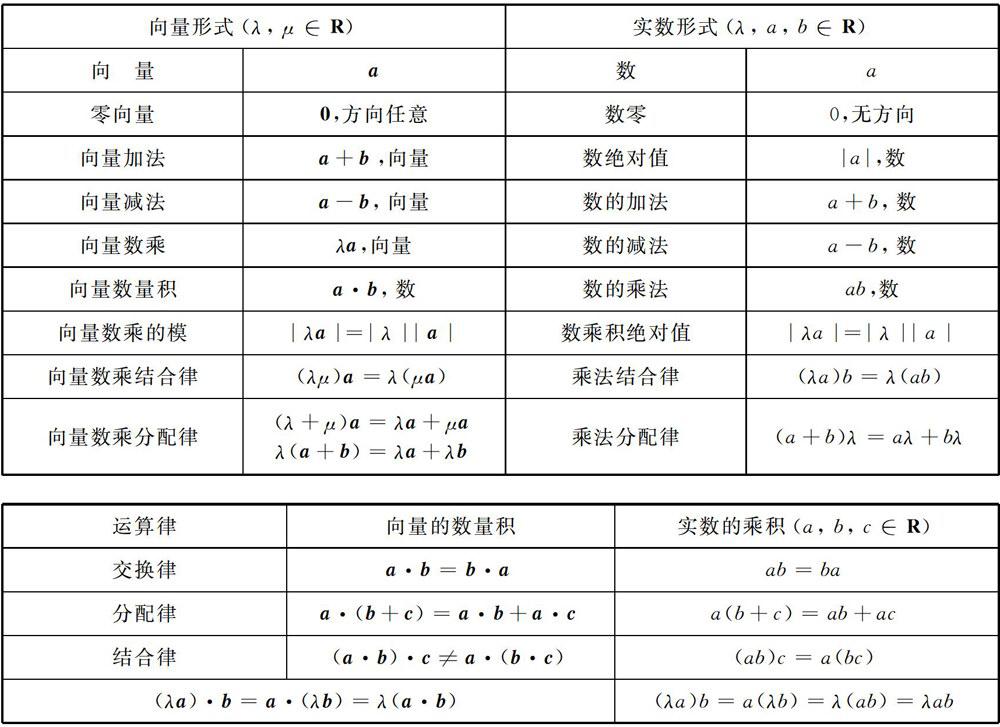
向量具有代數形式與幾何形式的“雙重身份”，既是代數的對象，又是幾何的對象.作為代數對象的向量，必有運算法則和運算律，可與實數進行類比.

實數的運算結果始終是數，α十b，α-b，λα運算結果仍是向量，而向量的數量積（點乘）運算結果不是向量了.如果說從數的運算到字母的運算是運算的一次飛躍，那么運算對象擴展到向量則是運算認識上又一次飛躍.

三、向量是解決幾何問題的重要工具

向量是既有大小、又有方向的量，是通過代數運算刻畫幾何對象及其位置關系、幾何度量問題的工具.

解法1中，建立坐標系，將幾何問題代數化（可以是三角形式），通過代數運算解決.解法2借助圖形將抽象的問題直觀地表達出來，使問題變得更直觀、簡單，求解更快速、準確.

向量是數形結合的載體，向量的坐標表示把點與數聯系了起來，既為我們用代數方法研究幾何問題提供了可能，也為我們用幾何的觀點處理某些代數問題豐富了研究的范圍和手段，這正是向量已成為中學數學課程的主角的原因所在.