Richardson迭代法的松弛策略

韓光輝, 渠剛榮

(北京交通大學(xué) 理學(xué)院, 北京 100044)

圖像重建(如電學(xué)層析成像、 計(jì)算機(jī)層析成像等)的實(shí)驗(yàn)過程可歸納為線性方程組模型

Ax=b,

重建圖像的問題即轉(zhuǎn)化為線性方程組的求解問題. 但通常情況下, 因?yàn)閷?shí)驗(yàn)誤差導(dǎo)致方程組沒有相容性, 很難找到方程組的精確解, 所以采用迭代算法尋找方程組的近似解. Richardson迭代算法[1]即為其中一種, 計(jì)算公式如下：

x(n+1)=x(n)+α(b-Ax(n)),

(1)

其中α是松弛參數(shù), 用α取值控制Richardson迭代算法的收斂性和收斂速度. 目前, 關(guān)于Richardson迭代算法的研究已有許多結(jié)果[2-12]. 文獻(xiàn)[4]考慮系數(shù)矩陣A為對(duì)稱正定的情形, 利用Tschebyscheff不等式選取松弛參數(shù)α的取值, 該取值方法依賴于矩陣A特征值的下界和上界, 需對(duì)矩陣A的所有特征值上、 下界進(jìn)行估計(jì)； 文獻(xiàn)[5]提出了松弛參數(shù)取值為α=2/(λlow+λup), 其中λlow,λup分別是對(duì)稱正定矩陣A所有特征值的下界和上界； 文獻(xiàn)[6]給出了Richardson迭代法的收斂性證明; 文獻(xiàn)[7]針對(duì)矩陣A是非對(duì)稱的情形給出了收斂性證明； 文獻(xiàn)[8]討論了復(fù)數(shù)線性系統(tǒng)下Richardson迭代法的收斂性, 將松弛參數(shù)α視為一個(gè)取值變化的參數(shù)αn, 并給出一種取值方法:

其中ψ(ω)=τω+τ0+τ1ω-1+τ2ω-2+…; 文獻(xiàn)[9-10]在對(duì)稱正定矩陣A的情形下, 對(duì)松弛參數(shù)的取值給出了更明確的結(jié)論： 當(dāng)松弛參數(shù)滿足0<α<2/λmax時(shí), Richardson迭代法收斂, 且松弛系數(shù)的最優(yōu)取值為2/(λmin+λmax), 這里λmin,λmax分別是對(duì)稱正定矩陣A的最小和最大特征值. 文獻(xiàn)[11]考慮到最小特征值不易計(jì)算, 利用矩陣A對(duì)角線上最小的元素替代最小特征值λmin, 得到了一個(gè)新的常數(shù)步長(zhǎng), 并證明了該迭代法的收斂性； 文獻(xiàn)[12]針對(duì)A為對(duì)稱正定矩陣的情形, 將Richardson迭代法與其他幾種基本迭代算法進(jìn)行對(duì)比, 得出結(jié)論： 隨著迭代矩陣譜半徑的逐漸變小, 迭代算法的收斂速度越來越快.

本文將Richardson迭代算法推廣到求解更一般的線性方程組, 如系數(shù)矩陣A是非對(duì)稱方陣的情形. 利用相似變換矩陣重新表示Richardson迭代算法的迭代過程和迭代矩陣, 根據(jù)新的迭代矩陣給出一種最優(yōu)松弛策略及一種僅依賴于最大特征值的加速收斂策略, 并證明了松弛策略的有效性.

1 預(yù)備知識(shí)

p1+p2+p3+…+pm=N.

特征值的大小順序?yàn)?<λ1<λ2<…<λm, 對(duì)應(yīng)的線性無(wú)關(guān)特征向量記作ξk,j(1≤k≤m, 1≤j≤pk), 則有

Aξk,j=λkξk,j.

根據(jù)相似對(duì)角矩陣的性質(zhì), 矩陣A相似于一個(gè)對(duì)角矩陣[13]. 記Pk=(ξk,1,ξk,2,…,ξk,pk), 則存在非奇異矩陣P=(P1,P2,…,Pm), 使得

P-1AP=Λ=diag(λ1Ip1,λ2Ip2,…,λmIpm),

(2)

這里,Ipk表示pk階單位矩陣. 矩陣A所有的線性無(wú)關(guān)特征向量ξk,j可構(gòu)成空間N的一個(gè)基. 若用x+表示方程組(1)的唯一解, 則x+可線性表示為

(3)

且

(4)

其中ck,j∈,k=1,2,…,m,j=1,2,…,pk. 此外, 迭代初始解x(0)可表示為

(5)

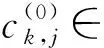
定理1對(duì)于n=1,2,…, 由Richardson迭代公式(1)得到的迭代解x(n)可表示為

x(n)-x+=(I-αA)n(x(0)-x+)=Pdiag((1-αλ1)nIp1,…,(1-αλm)nIpm)r,

(6)

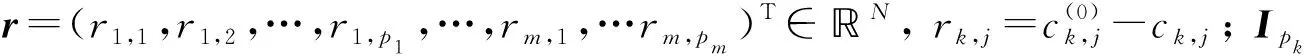
證明: 根據(jù)式(1)和式(4), 可得

x(n+1)-x+=x(n)-x++αA(x+-x(n))=(I-αA)(x(n)-x(+)),

(7)

利用遞推式(7)可得

x(n)-x+=(I-αA)n(x(0)-x+),

由式(3)和式(5), 可得

x(0)-x+=(P1,P2,…,Pm)r,

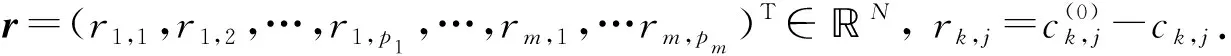
證畢.

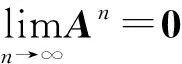
令D(α)=diag((1-αλ1)Ip1,…,(1-αλm)Ipm), 則根據(jù)定理1可得

[D(α)]n=diag((1-αλ1)nIp1,…,(1-αλm)nIpm),

x(n)-x+=P[D(α)]nr.

根據(jù)定理2可得使Richardson迭代法收斂的一個(gè)充要條件.

定理3對(duì)于由Richardson迭代法得到的逼近序列{x(n)}, 其收斂于方程組唯一解x+的充要條件是: 松弛參數(shù)α滿足不等式0<α<2/λm.

證明: 為保證收斂性成立, 需要

[D(α)]n→0,n→∞,

根據(jù)定理2, 逼近序列{x(n)}收斂于x+的充要條件是ρ(D(α))<1. 由于D(α)是一個(gè)對(duì)角矩陣, 且其對(duì)角元素為(1-αλ1),…,(1-αλm), 所以

當(dāng)α<0或α≥2/λm時(shí), 因?yàn)閨1-αλm|≥1, 所以ρ(D(α))≥1. 當(dāng)0<α<2/λm時(shí), 有|1-αλm|<1. 因?yàn)?<λ1<λ2<…<λm, 所以

0<α<2/λm<2/λk, 且|1-αλk|<1,k=1,2,…,m-1.

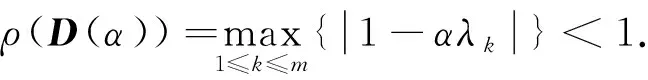
2 松弛策略

下面給出Richardson迭代法的最優(yōu)松弛參數(shù)和加速收斂策略. 定義迭代誤差為

ε(n)∶=x(n)-x+,n≥0.

根據(jù)式(6), 定義迭代矩陣為

G(α)=Pdiag((1-αλ1)Ip1,…,(1-αλm)Ipm)P-1,

則有迭代誤差表達(dá)式

ε(n+1)=G(α)ε(n),n=0,1,2,…

其中ε(0)=Pr. 迭代法收斂的一個(gè)充分條件是ρ(G(α))<1, 且譜半徑越小, 收斂速度越快. 因此, Richardson迭代算法中的最優(yōu)松弛策略是指使迭代矩陣的譜半徑達(dá)到極小值.

定理4對(duì)任意一個(gè)迭代初始解x(0), Richardson迭代算法的最優(yōu)松弛參數(shù)是

αopt=2/(λ1+λm),

其中λ1,λm分別是系數(shù)矩陣A的最小和最大特征值.

證明: 由于0<λ1<λ2<…<λm, 所以對(duì)于α>0, 有

1-αλ1>1-αλ2>…>1-αλm,

因此

ρ(G(α))=max{|1-αλ1|,|1-αλm|}.

(8)

又由于

(9)

這里k=1,m. 于是, 根據(jù)式(8)和式(9), 可得

(10)

由式(10), 可得

ρ(G(α))=max{1-αλ1,αλm-1},α>0.

(11)

函數(shù)ρ(G(α))的極小值點(diǎn)應(yīng)在直線y=1-αλ1與直線y=αλm-1的交點(diǎn)處取得, 即

1-αλ1=αλm-1.

(12)

由方程(12)解得最優(yōu)松弛參數(shù)αopt. 證畢.

定理5對(duì)于任意的α(1)∈(0,1/λm), 其關(guān)于點(diǎn)α=1/λm對(duì)稱點(diǎn)的坐標(biāo)為α(2)=2/λm-α(1), 即α(2)∈(1/λm,2/λm), 則有ρ(G(α(2)))<ρ(G(α(1))).

證明: 根據(jù)式(10)和式(11), 可得

因?yàn)?/λm<2/(λ1+λm), 所以

ρ(G(α(1)))=1-α(1)λ1, 0<α(1)<1/λm.

對(duì)于α(2)=2/λm-α(1)∈(1/λm,2/λm), 分兩種情形討論：

情形1) 當(dāng)1/λm<α(2)<2/(λ1+λm)時(shí), 有

ρ(G(α(2)))=1-α(2)λ1<1-α(1)λ1=ρ(G(α(1)))；

情形2) 當(dāng)2/(λ1+λm)<α(2)<2/λm時(shí), 因?yàn)棣?2)=2/λm-α(1), 所以有

ρ(G(α(2)))=α(2)λm-1=1-α(1)λm<1-α(1)λ1=ρ(G(α(1))).

綜上可知結(jié)論成立. 證畢.

3 數(shù)值實(shí)驗(yàn)

例1求解線性方程組Ax=b, 其中:

x(n+1)=Qx(n)+q,

圖1為與最優(yōu)松弛系數(shù)對(duì)應(yīng)的迭代誤差對(duì)比結(jié)果, 其中α-和α+分別表示取值比αopt小和比αopt大的α. 由圖1可見, 當(dāng)松弛參數(shù)α=αopt時(shí), Richardson的收斂速度較快. 表1列出了當(dāng)松弛參數(shù)取不同數(shù)值時(shí)對(duì)應(yīng)迭代矩陣的譜半徑. 由表1可見, 當(dāng)松弛參數(shù)α=αopt時(shí), 迭代矩陣的譜半徑最小.

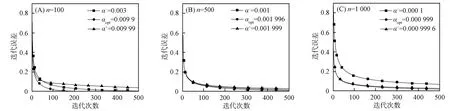
圖1 與最優(yōu)松弛系數(shù)對(duì)應(yīng)的迭代誤差對(duì)比Fig.1 Comparison with iterative error corresponding to optimal relaxation coefficient

表1 對(duì)應(yīng)最優(yōu)松弛策略的譜半徑對(duì)比

圖2為對(duì)應(yīng)定理5(加速收斂松弛策略)迭代誤差的對(duì)比結(jié)果, 其中αmid=1/λm, 另外兩個(gè)松弛參數(shù)α(1),α(2)的取值是關(guān)于αmid=1/λm對(duì)稱的. 由圖2可見, 當(dāng)松弛參數(shù)α=α(2)時(shí), Richardson迭代法的收斂速度較快. 表2列出了在松弛參數(shù)分別取α=α(1),α=αmid,α=α(2)時(shí)對(duì)應(yīng)的迭代矩陣譜半徑. 由表2可見, 對(duì)應(yīng)α=α(2)迭代矩陣的譜半徑比對(duì)應(yīng)α=α(1)迭代矩陣的譜半徑小.

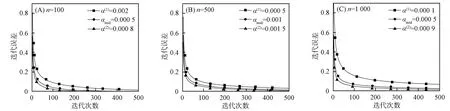
圖2 與加速收斂松弛策略對(duì)應(yīng)的迭代誤差對(duì)比Fig.2 Comparison with iterative error corresponding to accelerating convergence relaxation strategy

表2 對(duì)應(yīng)加速收斂松弛策略的譜半徑對(duì)比

綜上, 本文通過將以往在Richardson迭代法中要求系數(shù)矩陣為對(duì)稱正定矩陣的條件弱化為非對(duì)稱可逆矩陣的情形, 利用相似變換矩陣對(duì)Richardson方法的迭代過程和迭代矩陣進(jìn)行重新表示, 得到下列結(jié)論：

1) 對(duì)于由Richardson迭代法得到的逼近序列{x(n)}, 使其收斂于線性方程組唯一解的充要條件是松弛參數(shù)α滿足不等式 0<α<2/λm;

2) 利用迭代矩陣的新表達(dá)式, 基于使迭代矩陣的譜半徑達(dá)到極小值, 證明了最優(yōu)松弛參數(shù)為αopt=2/(λ1+λm)；

3) 針對(duì)用反冪法不易求出高階矩陣的最小特征值, 不易使用結(jié)論2)提出的最優(yōu)松弛參數(shù)的問題, 提出一種僅依賴于最大特征值的加速收斂策略α∈(1/λm,2/λm).