高中數學函數題多元化解題例析

丁 穎

(江蘇省常州戚墅堰實驗中學 213000)

高中數學中函數的問題包含眾多重難點，也是學生學習中反饋問題最多的知識模塊.對于面臨升學壓力的高中生而言，各種訓練題、模擬題層出不窮，盡管不提倡題海練習，但多數學生和教師依舊疲于奔命、樂此不疲.從題海中多加鍛煉提升學生應試能力，但究竟何處是岸？培養學生一題多解，進行多元化解題，可以從經典例題中尋求解題突破，培養高效解題習慣，發揮經典函數題目的資源優勢.結合幾例高中數學函數題，闡述多元化解題，突破函數解題思想禁錮.

一、多元解題的思維模式

1.發散思維

數學函數解題中多元化解題方式是以綜合角度進行思考，學生們在練習過程中，擺脫傳統例題教學中一種解題方案的狹隘認識，通過一題多解的訓練方法，為學生建立系統、全面的知識網絡，從一個任務目標出發思考多種解題可能性，提供多元化的解題方案，發散思維的應用拓展解題思路.

2.逆向思維

思維過程具有方向性，逆向思維在多元化函數解題過程中同樣扮演著重要的作用.一些函數問題從條件入手會變得復雜，嘗試從問題倒推可能會有不同的解題辦法，運用逆向思維可以擺脫正向思維的禁錮，提供更多解題方案.

3.創新思維

創新思維可以改變單一命題結論、形式，在解題思路上形成多元，從命題角度分析解決問題的可能性，從命題形式、內容、解題能力、思維方式等方面進行創新，使學生的思維更加靈活，激發解題創造力和創新能力.

二、高中數學函數多元解題例題探析

1.關于函數值域問題的多元化例題解析

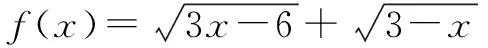
分析確定該題是無理函數的求值域或最值的問題，在高中數學函數解題中經常遇到，在各種模考卷和高考題中算常見類型.題目短小精悍，但解題方法多樣，可以涵蓋高中階段眾多數學知識，對學生知識的綜合應用能力和解題思路的鍛煉十分有益，體現學生的數學核心素養.

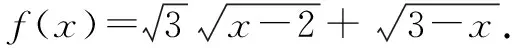
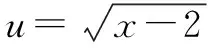
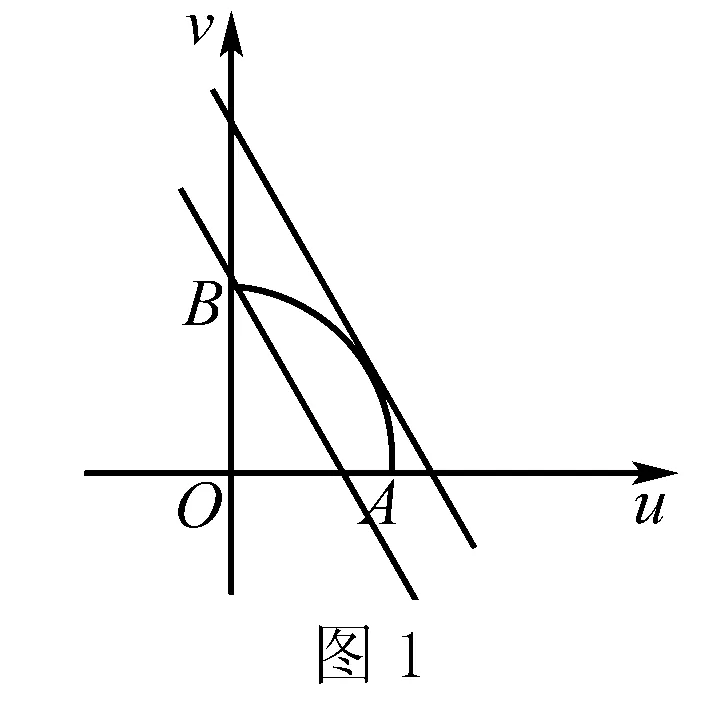
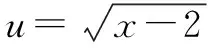
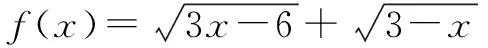
此外，該題目還可以借助一階導數以及函數的單調性求解，或者借助二階導數和函數的凹凸性求解.由于文章篇幅有限，不再一一贅述，提供上述常用且學生容易掌握的幾種解題思路，以便參考.

三、函數最值問題的多元化解題探析

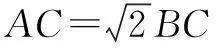
方法1 借助三角函數和函數相關知識解題.

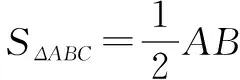
根據余弦定理可得

代入①式，

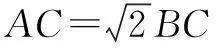
從該例題的解題方法可見，方法2具有原理一致性,在“阿波羅尼斯圓”的理論背景下解決的,所以我們主要是理解“阿波羅尼斯圓”的由來及其概念,而并非一定需要使用其相關結論來解決問題.