基于直升機艦面起降動態仿真的風限圖計算

吉洪蕾，趙輝, 陳仁良，吳文韜

1. 重慶大學 航空航天學院，重慶 400030 2. 南京航空航天大學 航空宇航學院 直升機旋翼動力學國家級重點實驗室，南京 210016 3.中國船舶工業系統工程研究院， 北京 100094

直升機艦面起降的風限圖(Wind-Over-Deck,WOD)是指某一特定機/艦組合在不同海況、晝夜環境和不同進場方向等條件下，直升機在其載艦上安全起降的最大相對風速、風向限制[1]。風限圖是保障直升機艦面起降安全的重要依據，在執行艦面起降任務之前駕駛員觀察艦船相對風向、風速是否位于風限圖內判定該任務能否完成。如果實際使用的風限圖大于真實的風向風速限制，會危及直升機艦面起降安全；反之，則會降低機/艦動態配合的任務效能。目前確定風限圖的主要手段仍然是直升機與載艦的動態配合試飛，盡管該方法能夠考慮各方面因素影響、試飛結果真實，但是耗資多、周期長、風險大、受環境條件限制[2]，迫使各軍事技術強國尋找替代方法。采用理論方法計算風限圖，不僅能夠克服機/艦動態配合試飛的諸多缺點，還能用于直升機艦面起降安全的影響因素分析，獲得廣泛關注。

孫文勝[3]采用二維定常CFD方法計算艦船尾流，較早地開展了直升機艦面起降風限圖的理論計算研究。艦面起降的危險狀況常常發生于直升機懸停在艦面起降點上方跟進艦船運動時，根據這一特點，建立了耦合艦船尾流的飛行動力學模型，提出了直升機艦面起降的最大姿態、操縱和功率約束等風限圖計算判據，通過求解直升機在起降點上方某一危險高度艦船尾流中的飛行動力學平衡方程獲得直升機狀態和駕駛員操縱量，與風限圖計算判據對比得到最大的風速風向限制，繪制風限圖，形成了直升機穩態配平的風限圖計算方法。孫傳偉等[4]進一步探索了艦面上層建筑“陡壁效應”引起的艦船尾流三維空間變化對直升機平衡的影響，指出飛行甲板上方由于機庫導致的垂向氣流及其分布對艦載直升機懸停操縱特性影響較大，而側向分量影響較小。趙唯義和王占勇[5]采用縮比艦船模型的風洞試驗數據分析了艦船尾流下洗、側沖以及渦流對直升機操穩性能的作用機理。李軍亮等[6]研究了側風對艦載直升機懸停狀態和駕駛員操縱的作用，發現小風速時側風對直升機平衡狀態的作用較小，然而大風速時容易導致尾槳操縱量超過安全操縱極限。基于大量的直升機岸基懸停試驗數據和駕駛員感受描述，Hoencamp和Pavel[7]總結了直升機艦面起降風限圖的理論計算判據。徐廣等[8-9]求解穩態艦船尾流中的直升機平衡方程，研究了UH-60A直升機在國外某航母甲板空氣流場中的平衡與著艦策略，指出駕駛員通過調整直升機航向姿態保持迎風方向進場能夠減少氣流的干擾，提升著艦的安全性。

上述風限圖的穩態配平計算方法固然能夠捕捉到起降點上方艦船尾流沿空間非均勻變化的作用，然而直升機艦面起降是一個動態過程，當直升機快速飛過隨時間和空間變化的艦船尾流場時，可能導致飛行狀態和需要的駕駛員操縱發生劇烈變化，駕駛員對快速變化的直升機狀態的應對能力也有重要影響，現有方法由于無法考慮到這些因素的作用，導致風限圖計算的準確度受到限制。雖然也有研究人員開展了艦船非定常尾流的數值模擬[10-14]和直升機艦面起降的動態仿真研究[15-22]，但由于集成艦船非定常尾流的直升機飛行動力學模型計算效率低，尚未用于風限圖的理論計算。

基于耦合艦船非定常尾流的直升機飛行動力學高效率計算模型，本文首先建立適于多軸協同操控的駕駛員模型，控制直升機飛行動力學模型完成艦面起降動態仿真，捕捉駕駛員感知、決策延誤和操控頻率限制的作用；然后發展多種艦面起降軌跡的數學描述及生成方法，以考慮不同起降方式導致艦船尾流時空變化的影響；最后將飛行動力學模型、駕駛員模型和艦面起降軌跡生成算法集成，形成全面計及艦船非定常尾流環境、直升機運動和駕駛員操控特點綜合影響的直升機艦面起降動態仿真方法，用于風限圖計算，提升風限圖計算的準確度。

1 耦合艦船非定常尾流的飛行動力學模型

耦合艦船尾流的飛行動力學模型是直升機艦面起降動態仿真和風限圖計算的基礎，難點在于隨時間和空間變化的艦船尾流與直升機飛行動力學模型的動態耦合建模。采用CFD方法計算艦面非定常流場，獲得離散數據樣本，建立艦船非定常尾流與飛行動力學模型的高效率動態耦合方法，形成耦合艦船非定常尾流的直升機飛行動力學模型。詳細的艦船尾流模擬、耦合艦船尾流的飛行動力學建模及驗證見文獻[20-21]。以UH-60直升機為例，最終得到的直升機艦面起降飛行動力學模型共21個運動自由度，具體包括機體的6個剛體運動自由度、旋翼4片槳葉的揮舞和擺振自由度、旋翼槳葉動態扭轉的1個自由度、旋翼動態入流的3個自由度、尾槳動態入流的1個自由度、機身的1個側洗和下洗自由度。簡化后的直升機飛行動力學方程組可以表示為

(1)

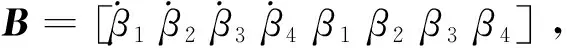
2 直升機艦面起降動態仿真方法

2.1 適用于多軸協同操控的駕駛員模型

實際的直升機艦面起降是一種復雜的多軸協同操控任務，然而艦載直升機往往具有良好的角速率穩定性和姿態操控性，即使直升機各軸響應間存在交叉耦合，駕駛員也可通過對各軸響應的補償實現解耦操控。因此，假設在艦面起降過程中駕駛員對直升機各軸響應的補償操控是獨立的，各軸操控的駕駛員模型可以單獨設計。基于上述假設，設計了適用于多軸協同操控的駕駛員模型，其結構如圖1所示，x,y,z為直升機縱向、橫向和垂向的位置坐標，vz為直升機垂向運動速度，YpΦ、YpΘ、YpΨ分別為滾轉、俯仰和偏航姿態駕駛員控制模型，Ypw為垂向速率駕駛員控制模型，Ypx、Ypy、Ypz分別為縱向、橫向和垂向位置駕駛員控制模型，Φcom、Θcom分別為滾轉和俯仰姿態駕駛員指令，vzcom為垂向速度駕駛員指令，xcom、ycom、zcom為要求駕駛員跟蹤的直升機縱向、橫向和垂向位置坐標，Ψcom為要求駕駛員跟蹤的直升機偏航角。

駕駛員的縱、橫向操控行為類似，模型分別由內環和外環兩個回路構成。其中，內環為姿態回路，主要功能是對直升機艦面起降過程的姿態角偏差進行補償。本文采用精確駕駛員模型[23-24]模擬這一過程，俯仰、滾轉姿態的駕駛員控制模型YpΘ(s)和YpΦ(s)為

(2)

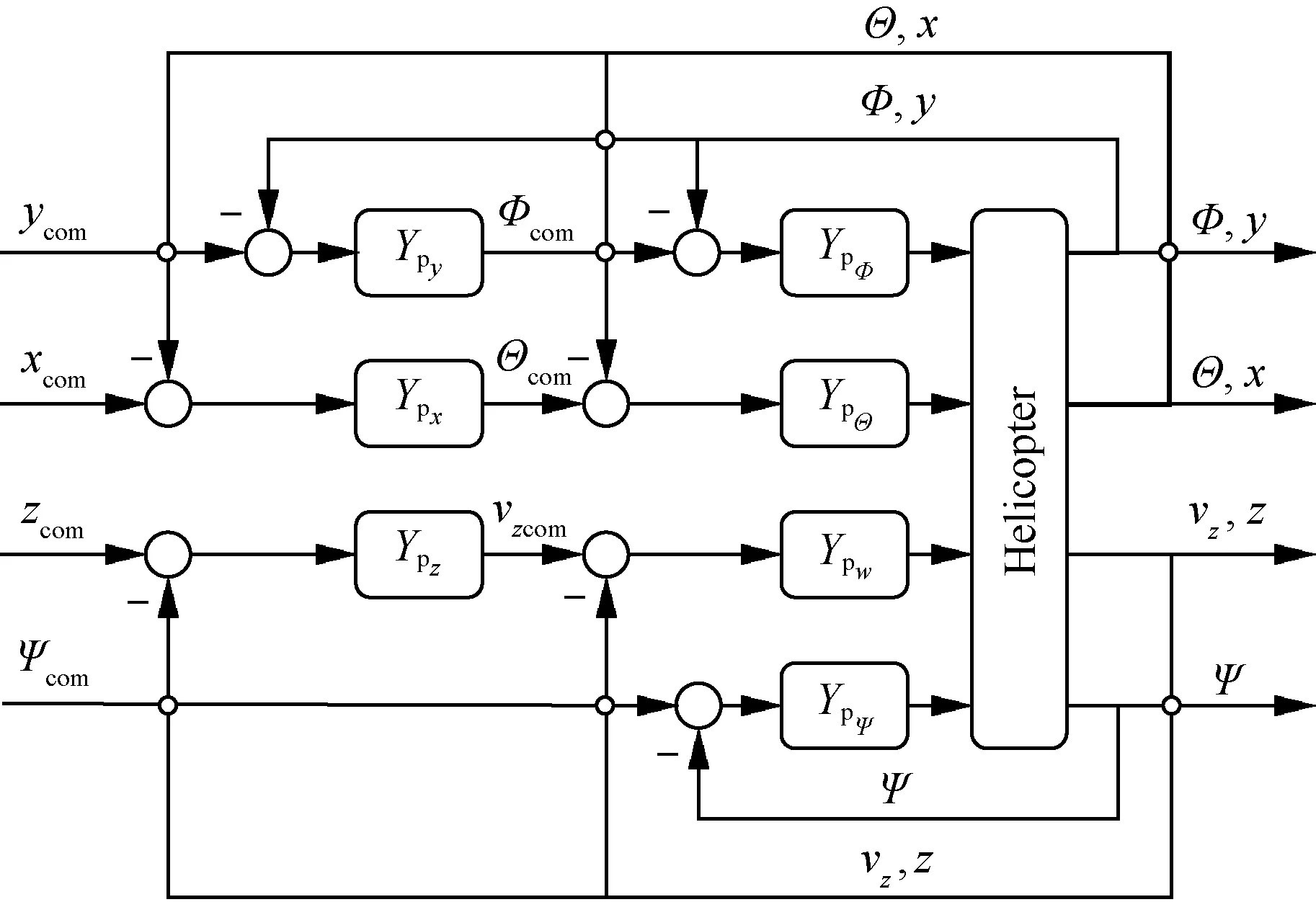
圖1 多軸協同操控的駕駛員模型Fig.1 Pilot model for multi-axis coordinated controls

式中：KpΘ和KpΦ分別為俯仰、滾轉姿態駕駛員控制模型增益，用來模擬駕駛員對控制變量誤差的應對能力。通過調整駕駛員控制模型增益KpΘ和KpΦ獲得期望的駕駛員與直升機組合系統穿越頻率ωcΘ和ωcΦ，使組合系統的幅值YpΘ/ΦYc(s)s=jω在穿越頻率處為1，即

YpΘ/ΦYcjωcΘ/Φ=1

Yc(s)為直升機飛行動力學模型；TLs+1/TDs+1為駕駛員模型的超前滯后環節，TL為超前時間常數，反映了駕駛員預測操控輸入的能力，TD為滯后時間常數，描述了駕駛員產生需要操控輸入的難易程度。根據駕駛員模型理論[23]，TL和TD的調整應使YpΘ/ΦYc(s)在穿越頻率附近具有以下形式:

式(2)中余下的兩項描述了駕駛員生理特征的限制，其中e-τs是一個延遲時間為τ的純時間延遲環節，用來模擬駕駛員決策過程導致的時間延誤，1/(TNs+1)描述了駕駛員操控的肌肉動力學特性。

外環為軌跡跟蹤控制，主要功能是跟蹤預定的飛行軌跡完成艦面起降任務。根據Hess等[25-26]的研究，縱、橫位置駕駛員控制模型YpX(s)和YpY(s)的選取應使直升機與駕駛員組合系統的縱、橫向位置響應在穿越頻率ωcX和ωcY附近具有與K/s類似的特性，本研究中YpX(s)和YpY(s)的形式為

(3)

式中：駕駛員控制模型增益系數KPX和KPY的選取應使外環位置回路穿越頻率為內環姿態回路穿越頻率的1/3[25]，即

(4)

縱、橫向內環姿態駕駛員控制模型的穿越頻率由直升機艦面起降任務的難易程度決定。預先對直升機艦面起降任務進行動態仿真，獲得起降過程中內環姿態響應的最大滾轉和俯仰角變化ΔΦmax和ΔΘmax，以及最大滾轉和俯仰角速率變化Δpmax和Δqmax，俯仰、滾轉操控的穿越頻率為[27]

(5)

對于垂向操控，以垂向速度回路為內環，駕駛員操控模型同樣采用精確駕駛員模型理論建立；垂向位置回路為外環，駕駛員模型僅由一個常數增益項構成。航向操控僅由偏航姿態駕駛員控制模型完成。垂向和航向的駕駛員操控模型設計過程與縱、橫向對應部分類似，這里不再贅述。

2.2 艦面起降軌跡的數學描述和生成

艦面起降空間狹小，起降甲板周圍存在諸多障礙物，且艦船尾部氣流環境復雜，根據起降場地和風況的不同應當因地制宜發展多種艦面起降方式，增加艦面起降的安全性。目前，國內外常用的直升機艦面起降方式包括從后向前起降、迎風起降、橫向起降、從前向后起降、艦艉起降和斜向起降6種[28]。上述6種起降方式的軌跡都可由穩定下滑、橫向平移、航向調整和起飛爬升這4個基本飛行軌跡組合而成。

1) 穩定下滑

在穩定下滑過程，駕駛員實施必要的操控使直升機從遠方到達艦船附近一點跟進艦船運動，直升機初始前飛速度降低至與艦船相同的速度，同時降低飛行高度，在下滑過程中還要保持相對恒定的下滑角。此任務可分為3個階段：初始階段，直升機在一定高度上作水平均速飛行，穩定下滑開始后，在垂向逐步過渡到以一定的加速度下降，在水平方向減速逐步達到設定的水平速度；穩定下滑階段，直升機在垂向保持恒定的加速度下滑，在水平方向保持恒定的加速度減速；終止階段，在水平和垂直方向的加速度逐漸降為零，垂向速度也逐漸降為零，直升機下降到一定高度跟進艦船運動，與艦船相對位置保持不變。

假設穩定下滑初始階段的直升機水平速度為Vg0，垂向位置為zg0，艦船航行速度為Vs，直升機和艦船的水平距離為Δxg0，設定的下滑角為γd，終止階段的直升機垂向位置為zgd，3個階段的開始時刻為t0、t1和t2，結束時刻為t1、t2和t3，每個階段所用時間為Δt1、 Δt2和Δt3，3個階段所用總時間為Δtf。沿慣性坐標系x軸的水平加速度的數學描述為

ax(t)=

(6)

沿慣性坐標系z軸的垂向加速度數學描述為

(7)

假設Δt1=Δt3=ctΔtf,ct為穩定下滑初始階段時間Δt1和終止階段時間Δt3所占穩定下滑總時間Δtf的比例系數，式(7)和式(8)均為參數ax2、az1、az2、ct和Δtf的函數，通過穩定下滑階段的下滑角約束、終止階段的水平和垂直方向速度和位置約束可求解上述參數，對加速度時間歷程積分得到直升機穩定下滑的速度和位移時間歷程。

2) 橫向平移

橫向平移開始前直升機位于艦船甲板起降點側方與艦船相對位置保持不變。橫向平移加速階段，直升機逐漸加速，直至達到設定的側向平移速度；然后是均速階段，保持設定的側向平移速度，直至接近艦面起降點上方；最后是減速階段，逐步將側向平移速度降為零，使直升機最終位于起降點上方跟進艦船運動。

假設直升機橫向平移加速、勻速和減速階段的開始時刻為t0、t1和t2，結束時刻為t1、t2和t3，3個階段所用時間為Δt1、 Δt2和Δt3。橫向平移加速度的數學描述為

ay(t)=

(8)

假設3個階段所用時間相同，即Δt1=Δt2=Δt3=Δtf/3，式(8)僅為ay2和Δtf的函數，給定最大橫向平移加速度ay2和橫向移動距離Δy，可以解得上述參數，對加速度時間歷程積分可得直升機橫向平移的速度和位移時間歷程。

3) 航向調整

當直升機位于艦面起降點上方時往往需要調整航向姿態，以適應直升機起飛或者降落時的風向限制。航向調整的偏航角加速度的數學描述為

α(t)=

(9)

假設Δt1=Δt3=Δt2/2=Δtf/4，給定航向調整的偏航角變化ΔΨ和最大偏航角加速度αΨ，可以解得Δtf，代入式(9)，積分可得偏航角速率和角度時間歷程。

4) 起飛爬升

典型的直升機艦面起飛爬升包括3個階段：初始階段，駕駛員操控直升機在垂向加速達到要求的爬升率，水平方向加速達到要求的水平加速度；穩定爬升階段，直升機保持恒定的爬升率和水平加速度飛行；終止階段，將爬升率和水平加速度降為零，直升機在指定高度穩定平飛。

假設直升機起飛爬升3個階段的開始時刻為t0、t1和t2，結束時刻為t1、t2和t3，所用時間為Δt1、 Δt2和Δt3。沿慣性坐標系x軸的加速度的數學描述為

ax(t)=

(10)

沿慣性坐標系z軸的加速度的數學描述為

az(t)=

(11)

假設Δt1=Δt3=ctΔtf，式(10)和式(11)均為參數ax2、az2、ct和Δtf的函數。給定允許的最大爬升加速度az2，通過起飛爬升終止階段的水平速度、垂向速度和高度約束可以解得上述參數，對加速度時間歷程積分可得直升機起飛爬升的速度和位移時間歷程。

2.3 直升機艦面起降的數值仿真方法

將駕駛員模型和艦面起降軌跡生成算法與耦合艦船非定常尾流的飛行動力學模型集成，構成圖2的直升機艦面起降數值仿真流程。其中，耦合艦船非定常尾流的直升機飛行動力學模型能夠反映艦船非定常尾流和直升機運動的作用，駕駛員模型能夠模擬駕駛員感知、決策延誤和操控頻率限制的作用，而采用多種艦面起降方式仿真可以研究飛行軌跡導致艦船尾流時空變化對直升機艦面起降安全的影響。本文采用一種變步長、變階數的Adams方法[29]對式(1)的直升機飛行動力學方程組積分模擬直升機的操縱響應，并采用雙線性變換方法將駕駛員模型與飛行動力學模型耦合求解，實現直升機艦面起降動態仿真，輸出直升機運動狀態和駕駛員操縱量，用于風限圖計算。

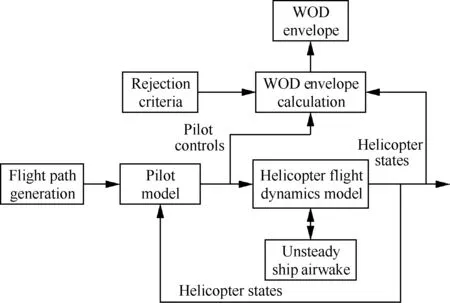
圖2 直升機艦面起降數值仿真流程Fig.2 Numerical simulation procedure of helicopter shipboard flight

3 直升機艦面起降風限圖計算方法

3.1 風限圖計算判據

直升機艦面起降安全的影響因素眾多，涉及艦船尾流環境、直升機運動、駕駛員操控和選擇的起降方式三方面。風限圖是針對特定的機/艦組合制定的，不同型號直升機的運動特性有差異，而不同型號艦船由于幾何外形和尺寸的差異，艦船尾流的時空分布也不同。因此，不同機/艦組合的動態配合特性不同，風限圖也不同。本文以UH-60直升機和LHA兩棲登陸艦組合為例計算風限圖，其中，UH-60直升機的飛行動力學建模見文獻[20-21]，LHA兩棲登陸艦模型如圖3所示，OSHiSHjSHKSH為艦船坐標系，具體的流場計算及驗證見文獻[20-22]。針對UH-60直升機的特點和相關規定[30]，選定如下約束條件作為該機/艦組合風限圖的計算判據。

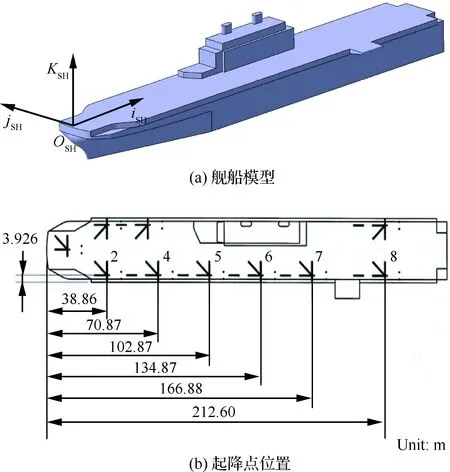
圖3 艦船模型及起降點位置Fig.3 Ship model and locations of its landing spots

判據1在任何方向的風速超過22.5 m/s、尾槳正側風大于17.5 m/s時禁止直升機艦面起降。

判據2直升機總距桿、縱/橫向操縱桿和尾槳腳蹬操縱余量均不小于10%。

判據3在艦船附近飛行時，直升機滾轉角不大于8°，俯仰角后倒不超過7°、前傾不超過4°。

判據4發動機可用功率余量不小于10%。

3.2 風限圖計算方法

根據3.1節建立的風限圖計算判據，首先采用穩態配平方法計算風限圖，然后采用直升機艦面起飛和降落的動態仿真進一步縮小風限圖范圍，提升風限圖計算的準確度。以穩態配平方法的風限圖計算結果為基礎，基于動態仿真的風限圖計算流程如圖4所示，具體過程如下：

步驟1從風向角θw=-90°、風速Uinf=Umθw開始，執行直升機艦面起飛和降落的動態仿真，將駕駛員操縱量和直升機運動狀態與風限圖計算判據對比，判斷是否超出。其中，θw為風向角，左舷為負，右舷為正；Umθw為穩態配平確定的風向角為θw的直升機懸停風速限制。如果是，將風速Uinf減小2.5 m/s，重新執行直升機艦面起降動態仿真；如果否，進入下一步。

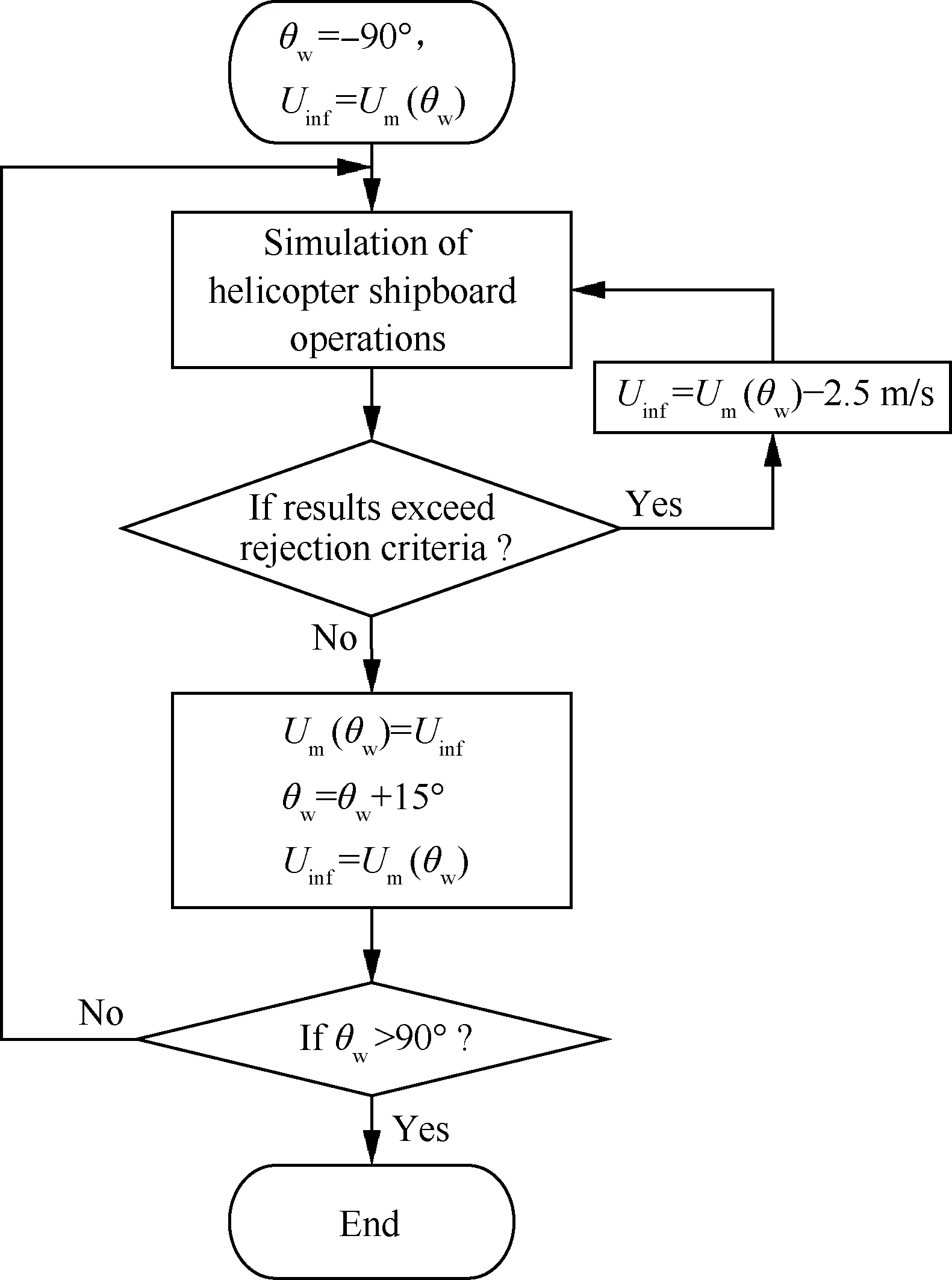
圖4 基于直升機艦面起降動態仿真的風限圖計算流程Fig.4 WOD envelope calculation procedure based on dynamic simulation of helicopter shipboard operations

步驟2在風向角θw的最大風速限制為Umθw=Uinf。將風向角θw增加15°，Uinf重新設為Umθw，進入下一步。

步驟3判斷風向角θw是否大于90°。如果是，終止計算；如果否，進入步驟1繼續計算。

4 計算結果與分析

首先采用斜向方式執行直升機艦面起飛和降落的動態仿真，并確定風限圖。斜向起飛和降落的軌跡由穩定下滑、航向調整和起飛爬升3個基本飛行軌跡組合而成，如圖5所示。圖6為直升機從艦面起降點上方斜向起飛的地速時間歷程，其中，地速坐標系的x和z軸與圖3(a)中艦船坐標系的x和z軸方向相反，兩個坐標系的y軸指向相同。

圖7～圖9為UH-60直升機在不同風況艦船尾流中斜向起飛的駕駛員操縱桿量、直升機姿態角和需用功率Preq時間歷程。圖7中，δlat為橫向操縱桿量，向右壓桿為正；δlon為縱向操縱桿量，向后拉桿為正；δcol為總距操縱桿量，總距增大桿量為正；δped為尾槳腳蹬操縱量，右踩為正。直升機起飛的起點位于艦面起降點8上方5 m，總重為8 500 kg。動態仿真的初始狀態由直升機在艦船尾流中的配平計算獲得。從圖中可以看出，艦船尾流對直升機艦面起飛操縱量、姿態和需用功率的影響非常大，風況變化使直升機在艦面起降過程中經歷不同的艦船尾流速度時空變化，導致直升機飛行狀態和需要的駕駛員操縱補償變化劇烈。雖然在圖中所有風況艦船尾流環境中直升機保持懸停的飛行狀態和駕駛員操縱量都位于風限圖判據內，但當風向角為左舷和右舷45°風況時，直升機艦面起降的腳蹬操縱和滾轉角分別超出了風限圖計算判據，表明在此風況下直升機雖然能夠安全地在起降點8上方懸停，但是以斜向方式起飛過程中受到艦船尾流時空間變化的強烈干擾，無法安全地完成起飛任務。

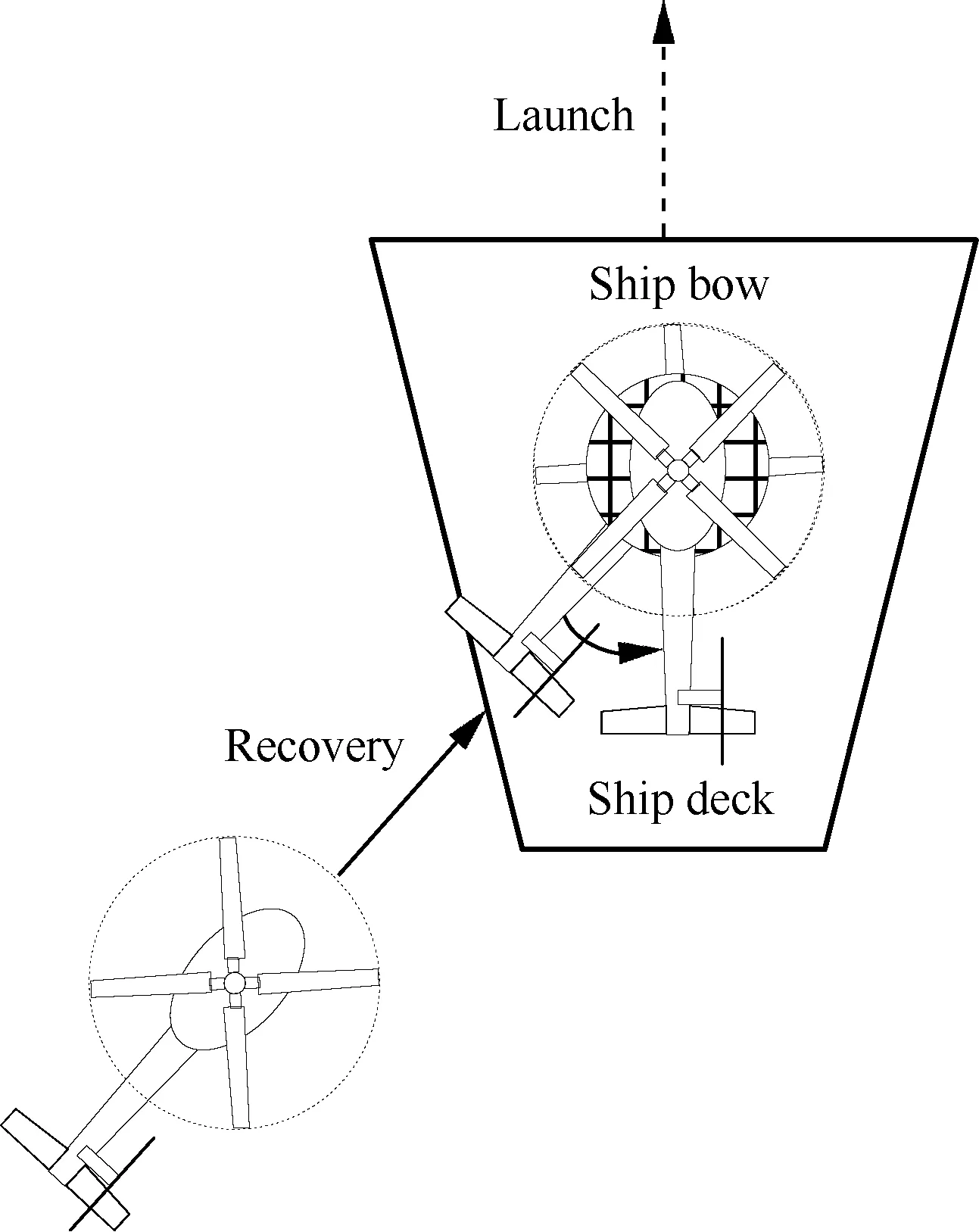
圖5 斜向起降方式示意圖Fig.5 Diagram of oblique procedure

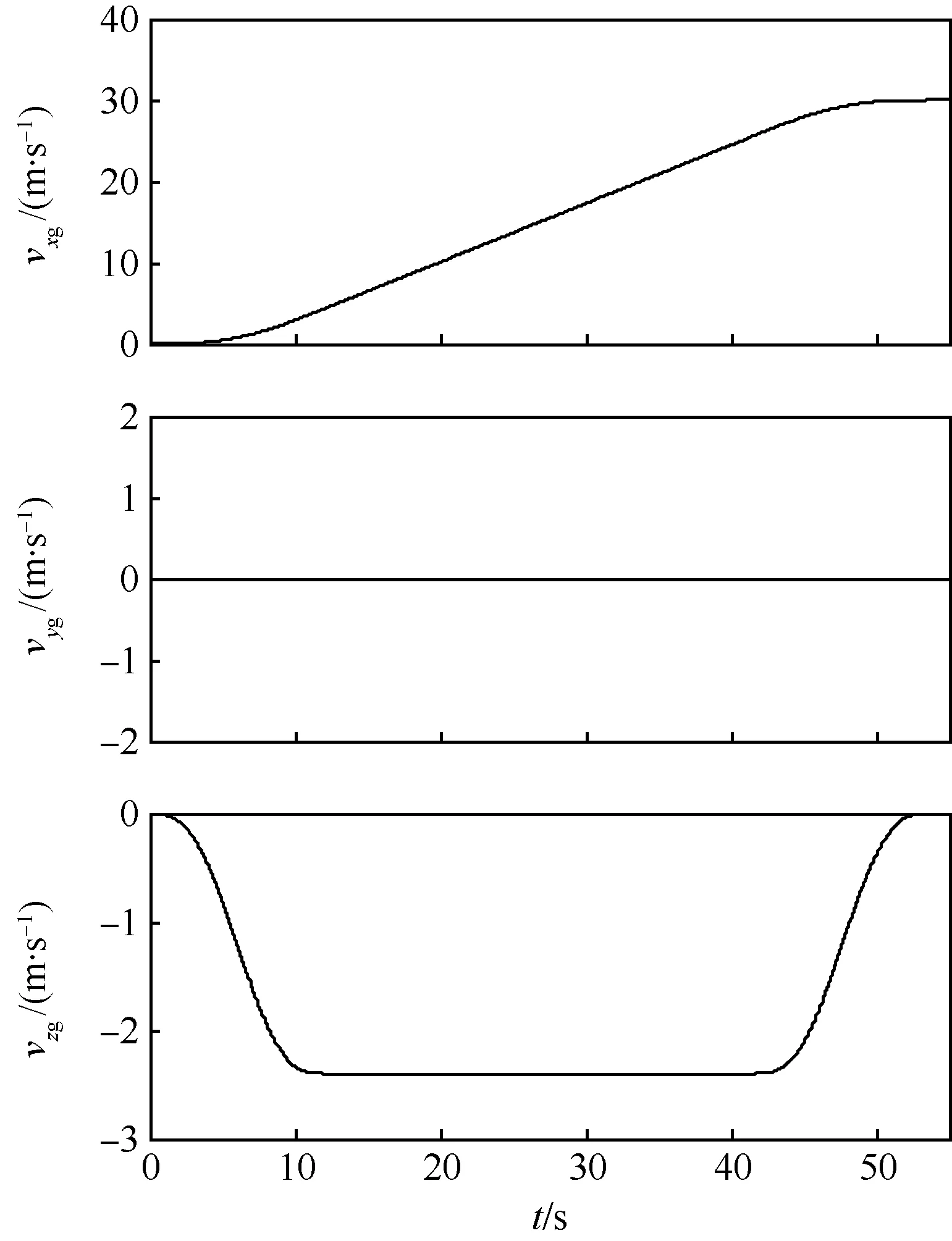
圖6 斜向起飛地速時間歷程Fig.6 Time history of ground velocities of oblique takeoff

圖7 斜向起飛駕駛員操縱時間歷程Fig.7 Time history of pilot controls of oblique takeoff

除了艦面起飛過程，還分析了直升機以斜向方式在艦面降落的動態響應，得到相似的結論，即：雖然在某些風況下直升機能夠安全地在艦面起降點上方保持懸停，但在降落過程中受到艦船尾流時空變化的強烈干擾，導致無法安全地完成降落任務。與起飛過程相比，在降落過程中當直升機逐漸接近艦船時，受到艦船尾流非定常時空變化的干擾更加強烈，導致直升機飛行狀態和需要的駕駛員操縱變化更劇烈，對直升機艦面起降的飛行安全和風限圖計算準確度的影響也更大。因此，風限圖的理論計算應同時考慮直升機艦面起飛和降落過程中艦船尾流時空變化的干擾。

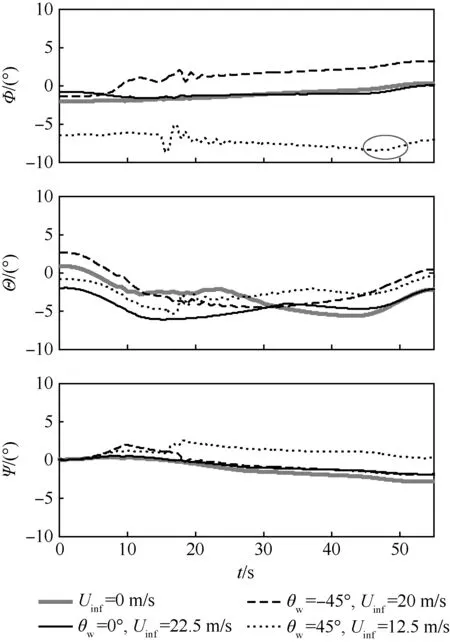
圖8 斜向起飛姿態角時間歷程Fig.8 Time history of attitudes of oblique takeoff

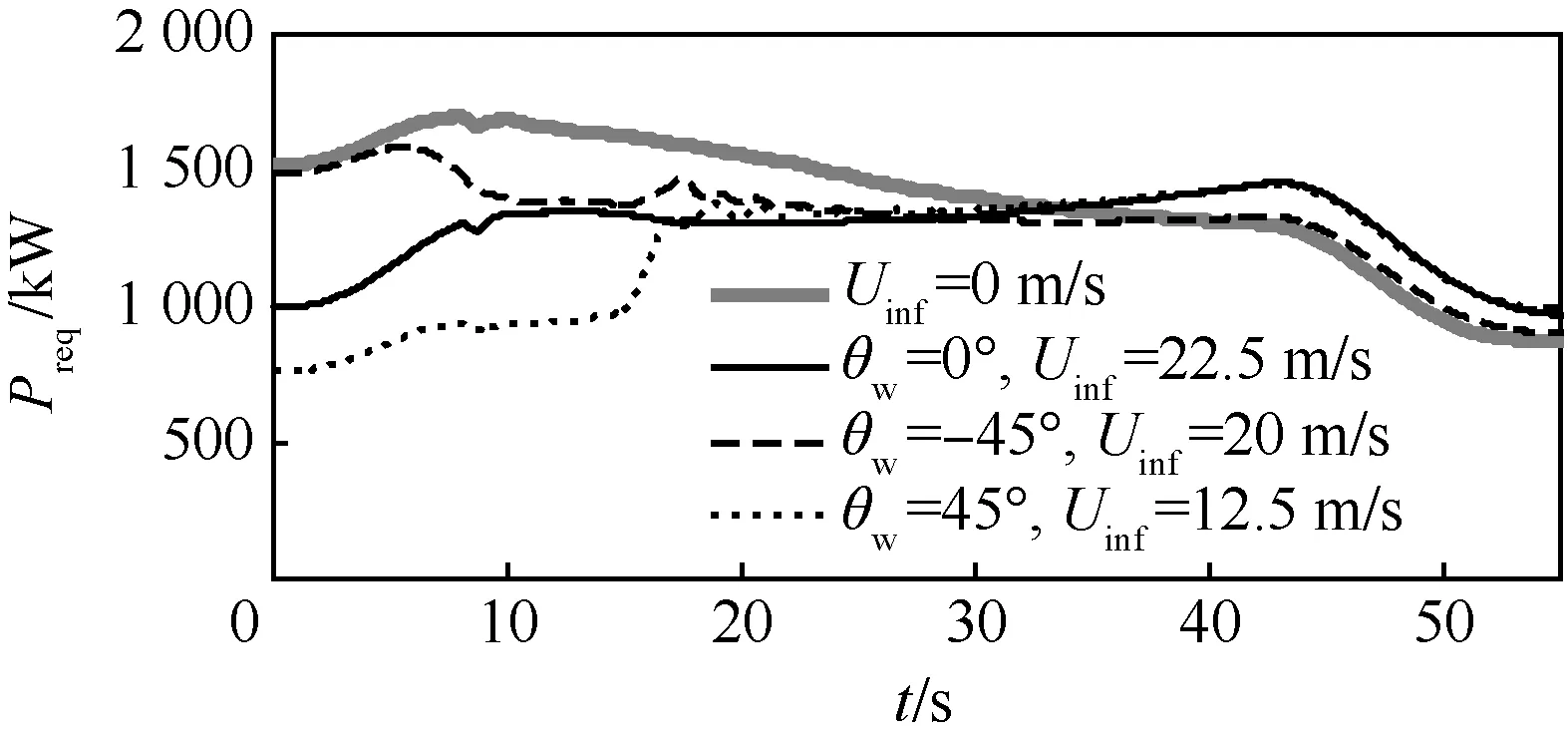
圖9 斜向起飛需用功率時間歷程Fig.9 Time history of required power of oblique takeoff

圖10為采用不同方法計算UH-60直升機在LHA艦起降點5、6和8上方艦面起降的風限圖，圖中極徑坐標為艦船前方來流風速Uinf，極角坐標為艦船前方來流風向角θw。穩態配平方法取自文獻[2]，并采用斜向起降方式執行直升機艦面起飛和降落的動態仿真，計入起飛和降落過程中艦船尾流的干擾計算風限圖。艦面起降過程中影響直升機飛行安全的因素也標于圖中，“Col.”表示總距操縱限制，“Ped.”表示腳蹬操縱限制，“Roll”表示滾轉角限制。兩種方法均采用本文提出的判據進行風限圖計算。起降點5、6和8的位置見圖3(b)。其中，起降點5位于艦面島型建筑左前方，起降點6位于島型建筑左側中間位置，起降點8位于島型建筑左后方。

從圖10中可以看出，總距、腳蹬操縱量和滾轉角是限制UH-60直升機在LHA艦安全起降的重要因素。由于艦面上層建筑的作用，不同起降點上方艦船尾流的空間分布存在差異，導致在起降點上方懸停和動態起降的直升機飛行狀態和駕駛員操縱量不同，直升機在3個起降點的風限圖也不同。穩態配平方法和動態仿真方法都能捕捉不同起降點上方艦船尾流的空間分布特征對風限圖理論計算的影響。

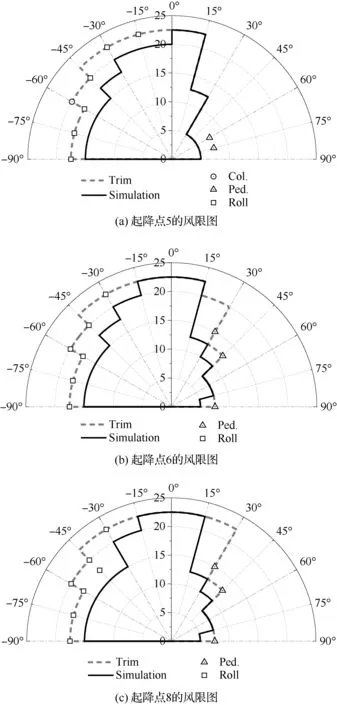
圖10 不同方法計算的直升機風限圖Fig.10 Predicted WOD envelopes of helicopter by different methods

與穩態配平方法計算的風限圖相比，采用艦面起降動態仿真方法計算的風限圖范圍更小。這是因為穩態配平方法只能考慮起降點上方艦船尾流的空間非均勻變化對直升機懸停的作用，而直升機艦面起降動態仿真方法不僅能考慮起降點上方艦船尾流的作用，還能捕捉直升機艦面起飛和降落機動過程中經歷的艦船尾流時空變化對直升機飛行狀態和駕駛員操控的影響。從上文分析可知，某些風況下直升機在艦面起降過程中受到艦船尾流的干擾遠大于在起降點上方懸停時受到的作用。因此，直升機艦面起降動態仿真方法顯著提升了現有風限圖計算方法的準確度。

為分析不同起降方式對直升機艦面起降風向、風速的限制，除了斜向方式，本文還采用從后向前方式進行直升機艦面起降動態仿真，得到直升機在起降點8上方艦面起降的風限圖，如圖11所示。圖中，“Power”代表直升機艦面起降過程的需用功率限制，作為對比，斜向起降的風限圖也繪于圖中。與斜向起降的風限圖相比，對于UH-60直升機和LHA艦船組合，從總體上看，采用從后向前起降方式能夠擴大直升機艦面起降的風速限制。這是因為從后向前起降將危險的直升機降落終點和起飛起點移至艦船側方，有效避開了起降點上方劇烈的艦船尾流時空變化對直升機飛行狀態和駕駛員操控的影響。然而，當艦面來流的風向角為右舷30°時，采用從后向前方式執行艦面起降任務容易導致直升機發動機的可用功率不足，這是因為當風向角為右舷30°風況時，直升機從后向前方式艦面起降的起點和終點恰巧位于島型建筑的下洗氣流內。因此，采用不同起降方式完成艦面起降使直升機經歷不同的艦船尾流時空變化，各有利弊。對于UH-60直升機和LHA艦組合，與斜向方式相比，采用從后向前方式執行直升機艦面起降的風速限制范圍更大，能夠提升機/艦動態配合的任務效能。采用從后向前方式進行直升機艦面起降動態仿真時，直升機總重為8 500 kg，從后向前起飛和降落的軌跡由穩定下滑、橫向平移和爬升飛行3個基本飛行軌跡組合而成，如圖12所示。

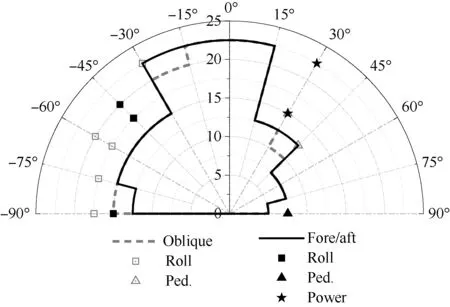
圖11 直升機以不同起降方式在起降點8的風限圖Fig.11 Predicted WOD envelopes of helicopter in landing spot 8 with different procedures

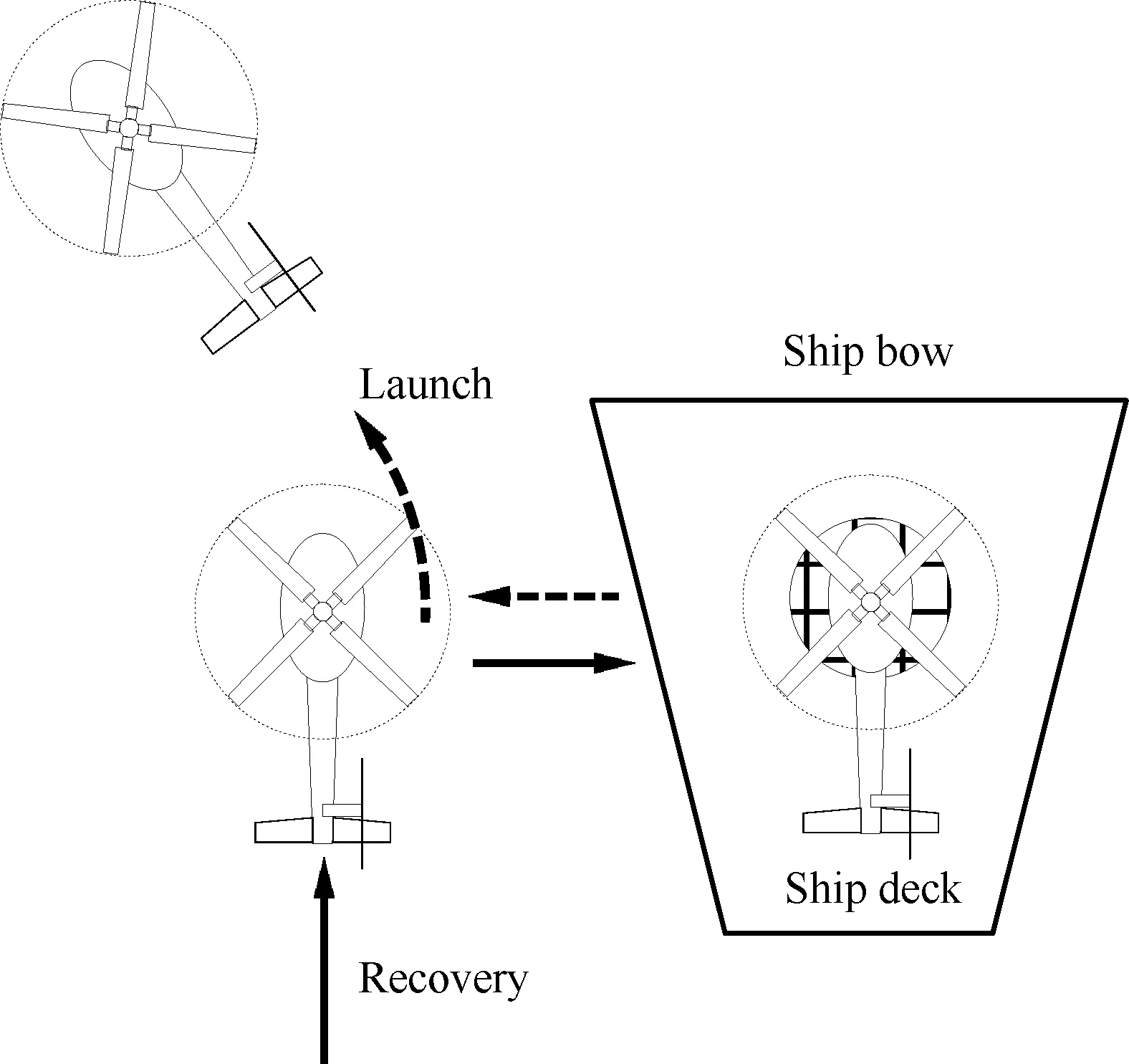
圖12 從后向前起降方式示意圖Fig.12 Diagram of fore/aft procedure

5 結 論

本文基于耦合艦船非定常尾流的飛行動力學模型，發展了適于多軸協同操控的駕駛員模型，建立了艦面起降軌跡的數學描述與生成方法，最終形成了直升機艦面起降的動態仿真方法。在此基礎上，建立了基于直升機艦面起降動態仿真的風限圖計算方法。

1) 常用直升機艦面起降方式的軌跡可由穩定下滑、橫向平移、航向調整和起飛爬升這4種基本飛行軌跡組合而成。本文的艦面起降軌跡數學描述與生成方法能夠給出光滑的飛行軌跡。建立的多軸協同操控駕駛員模型能夠控制飛行動力學模型跟蹤生成的飛行軌跡實現直升機艦面起降動態仿真。

2) 某些風況下直升機在艦面起降過程中受到艦船尾流的干擾遠大于在起降點上方保持平衡時受到的作用。基于直升機艦面起降動態仿真的風限圖計算方法不僅能考慮起降點上方艦船尾流沿空間非線性變化對直升機平衡狀態的作用，還能捕捉到不同起降方式導致艦船尾流時空變化對直升機飛行狀態和駕駛員操控的干擾，顯著提升了風限圖計算的準確度。

3) 采用不同起降方式在不同艦面起降點執行起飛和降落任務使直升機經歷不同的艦船尾流時空變化，直升機艦面起降的風向、風速限制也不同。對于UH-60直升機和LHA艦組合，與斜向起降方式相比，從后向前方式使直升機避開在起降點上方時空變化劇烈的艦船尾流中執行起飛和降落任務，風速限制范圍更大，能夠提升直升機艦面起降的任務效能。