循環加載下復合推進劑的能量耗散

童心，陳雄，許進升,，杜紅英，周長省

1. 南京理工大學 機械工程學院，南京 210094 2. 晉西工業集團有限責任公司 技術中心，太原 030027

以固體火箭發動機為動力的空空導彈在完整的壽命期內一般導彈要經歷運輸、貯存、掛載飛行、機動飛行和自主飛行等階段，會遇到溫度、濕度、振動、鹽霧和霉菌等一系列自然和誘發環境。其中，掛載飛行階段是空空導彈掛載在戰斗機上執行任務的主要階段，導彈彈體的振動頻率可高達幾千赫茲[1]。固體推進劑作為典型的黏彈性材料[2]，其循環應力-應變行為表現出明顯的滯后性，在循環載荷作用下機械能會由于滯后效應以熱能的形式耗散，但由于材料極低的導熱系數[3]，使得熱能無法在短時間內擴散到外界環境，因此材料內部和表面溫度有明顯的升高[4]。固體推進劑是溫度敏感材料[5]，溫度的急劇升高會極大地削弱其動態力學性能，進而影響發動機的內彈道性能。對經受振動的高填充比發動機而言，還會發生另一個問題：在振動期間，伴隨能量耗散引起的溫度升高會引起藥柱的膨脹，甚至充滿藥柱的自由容積。如果不具備足夠的自由容積，就有可能引起推進劑與推進劑、推進劑與殼體的接觸，這種接觸可能引起發動機局部溫度的上升，導致因推進劑力學性能降低而引起的結構破壞[6]。此外，由于固體火箭發動機在制造、貯存、運輸過程中受到溫度、振動等環境因素的影響，在推進劑內部易于形成微小裂紋、微孔洞等損傷，能量耗散會加快損傷的演化過程。因此，研究循環加載下復合推進劑的能量耗散具有十分重要的理論和工程意義。

圍繞固體火箭發動機在循環載荷下的響應，邢耀國等[7]通過實際觀測和數值仿真研究了艦載導彈上固體火箭發動機的疲勞壽命及其影響因素；關于固體火箭發動機受環境因素的影響，高艷賓等[8]分析了NEPE(高能硝酸酯增塑聚醚)推進劑在不同載荷水平下的疲勞損傷，并構建非線性損傷模型獲取了疲勞損傷的演化規律。然而，目前研究主要集中在循環力學性能和疲勞損傷方面，針對固體推進劑疲勞生熱的宏觀觀測及溫升預測報道較少[9]。實際上，材料的疲勞過程是一個復雜的能量耗散過程，包括彈性應變能[10]、塑性應變能[11]、黏彈性遲滯能[12]、熱耗散[13]、儲能[14]、聲發射、電磁等。對于復合固體推進劑而言，非彈性應變能(塑性應變能、遲滯能等)的很大部分以熱的形式耗散于環境中，引起材料自身溫度升高[15-16]。以往關于推進劑疲勞的研究通常假定推進劑變形時的溫度場與環境一致，這與循環載荷下推進劑變形伴隨著溫度升高的現象不符。

為深入研究復合推進劑在使用壽命中遭遇的能量耗散和滯后溫升問題，進行了應變控制模式下的疲勞實驗以獲取循環應力-應變特性；同時為獲取材料變形中的溫度場，借助非接觸式測溫裝置采集了推進劑試件疲勞變形時表面的實時溫度，分析了影響溫升的兩個重要因素。隨后建立物理模型和溫度場方程得到了導熱微分方程組，并利用有限元仿真對不同加載條件下推進劑的滯后溫升進行了預測。

1 實驗

1.1 材料和試件

研究對象為HTPB(Hydroxyl-Terminated PolyButadiene)三組元復合推進劑，各組元的質量分數為：鋁粉(Al)17%，高氯酸銨(AP)70%，粘合劑HTPB橡膠及其他組分13%。HTPB推進劑的密度、比熱容和導熱系數等參數見表1。

表1 HTPB推進劑的參數Table 1 Parameters of HTPB propellant

1.2 實驗裝置與方法

初次實驗時發現，HTPB推進劑較軟，難以直接固定在實驗設備的夾具上。為了改善夾持問題，消除不穩定加載或避免標距不精確，自行設計了與夾具適配的金屬夾頭(由45鋼制成)。夾頭和推進劑試件由兩液混合硬化膠粘接固定，根據圖1所示制備試件。在測試前，試樣放在保溫箱內保溫24小時以消除推進劑內部的殘余應力。

疲勞實驗在動態熱機械分析儀(Dynamic Mechanical Analyser，DMA，型號為美國BOSE公司的ELF3200)上進行。DMA主要由動磁式直線電機、溫控箱、力傳感器、位移傳感器、數據采集系統等組成。該系統能實現精確的位移和力控制，其靈敏度分別為0.01 mm和0.01 N。DMA的工作頻率范圍為1×10-5～2×102Hz。利用FLIR-A615型紅外熱像儀對HTPB推進劑試件表面溫度進行實時監測，紅外熱像儀的響應光譜范圍為7.5～14 μm，空間分辨率達到640 pixel×480 pixel。熱成像的采集頻率為25 Hz，熱分辨率在25 ℃時小于0.025 ℃，一般為0.02 ℃。實驗裝置如圖2所示。

參考GB/T 26077—2010《金屬材料疲勞軸向應變控制方法》，疲勞實驗采用了應變控制模式，對試件加載對稱正弦應變ε=εasin2πft，其中頻率f為1、10、50、100 Hz；實驗應變幅值εa=εmax-εmin/2為0.01、0.03、0.05，εmax為加載最大應變，εmin為加載最小應變；t為時間。實驗前，所有試件標距表面都需噴涂上一層黑色亞光漆，以避免發射光的干擾，提高試件表面熱輻射率。實驗中采集了標距內的最高溫度，下文出現的溫度均指試件標距內的最高溫度。

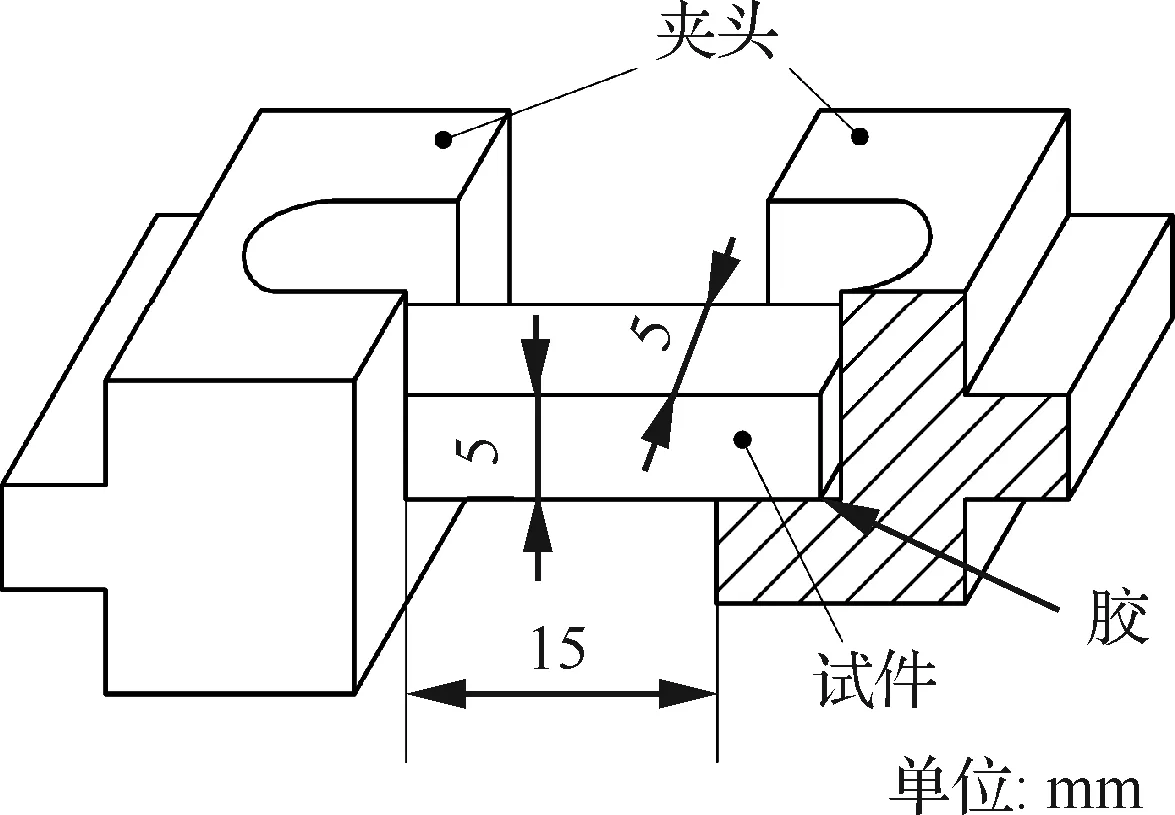
圖1 HTPB推進劑試件的裝夾Fig.1 Clamping of HTPB propellant specimen

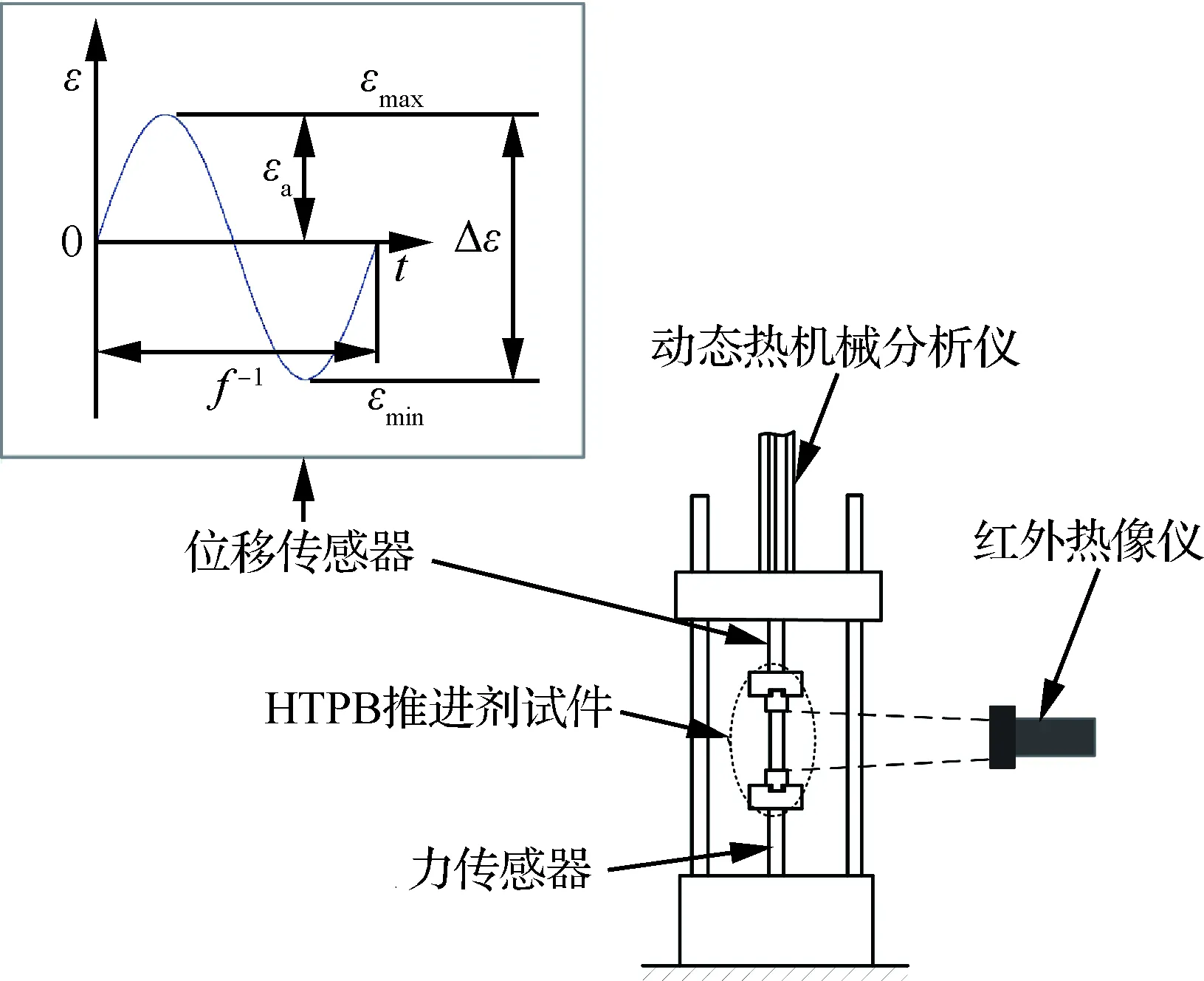
圖2 DMA與紅外熱像儀示意圖Fig.2 Schematic of DMA and infrared camera

2 循環應力軟化

圖3是HTPB推進劑在應變控制下的循環應力-應變關系(圖中N為疲勞次數)，可知循環應力-應變形成了滯回圈。在復合推進劑疲勞過程中，材料經歷了一個初始的“適應”階段后，應力幅達到一定穩定飽和值，在這種飽和狀態下出現穩定的滯后曲線。在疲勞“適應”過程中，材料內部微觀結構不斷發生變化，直到代表飽和狀態的穩定狀態出現為止。此后在材料的其余疲勞壽命周期，每周的滯回曲線基本保持不變。

值得注意的是，與金屬相比，聚合物在疲勞過程中只會發生循環軟化[17]，聚合物的成分、分子結構、溫度和應變速率在大范圍內變化也只能改變它的循環軟化程度。

文獻[18]指出，可利用“動態模量”來表征復合推進劑疲勞過程中應力軟化的程度。圖4給出了50 Hz、3種應變幅值下的動態模量，在疲勞次數達到10 000時，材料開始進入穩態狀態，動態模量變化幅度逐漸減小，對應著疲勞初始階段的應力降；動態模量最終趨于穩定值，意味著材料進入損傷穩定發展的狀態，機械能與熱能、儲能間的轉化達到了平衡。

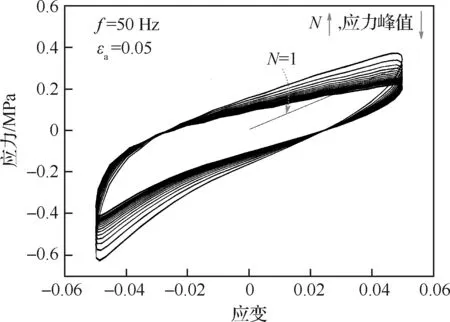
圖3 不同疲勞次數時的滯回圈Fig.3 Hysteresis loops at different fatigue cycles

圖4 動態模量隨疲勞次數的變化Fig.4 Variation of dynamic moduli with fatigue cycles

3 疲勞中的能量耗散與產熱

復合推進劑的疲勞是循環拉伸-回縮的過程。從分子機理看，受拉伸階段外力對推進劑體系做的功，一方面改變分子鏈段的構象，另一方面克服分子鏈段間的摩擦力；在回縮階段體系對外做功，一方面使構象改變重新卷曲，另一方面仍需克服鏈段間的摩擦力[19]。這樣在拉伸-回縮的循環中，分子鏈的構象完全恢復，不損耗功，所損耗的功全用于克服內摩擦力，轉化為熱。內摩擦力越大，滯后現象越嚴重，消耗的功(內耗)也越大。

3.1 滯彈性耗散

對于存在黏性的滯彈性[20]材料來說，若加載應變為ε(t)=ε0sinωt，其中ε0為應變幅值，ω為角頻率，則應力響應為

σ=σ0sin(ωt+δ)

(1)

式中：σ0為應力幅值；δ為滯后角(損耗角)，δ的正切值tanδ稱為損耗因子(或阻尼損耗系數)，用來表征材料的阻尼特性。ε(t)還可以寫為復數形式:ε*=ε0eiω t，則相應的應力響應為

σ*=σ0ei(ω t+δ)

(2)

復模量E*E*=E1+iE2為

(3)

E*的實數部分，即存儲模量E1表征材料存儲彈性變形能量的能力，其表達式為

E1=(σ0/ε0)cosδ

(4)

E*的虛數部分為損耗模量E2，體現材料黏性大小，表征材料耗散變形能量的能力，其表達式為

E2=(σ0/ε0)sinδ

(5)

復合推進劑屬于黏彈性材料，由于滯后阻尼效應，其應變落后于應力，表現出強烈的滯彈性，導致疲勞中的應力-應變關系形成滯回線。每一滯回圈耗散的機械能D0(即滯回曲線圍成的面積)為

(6)

式中：E*為動態模量。

表2給出了損耗角隨應變幅值和頻率的變化，其中損耗角均為滯回圈穩定時的測量值，當動態模量維持穩定時，損耗角也維持不變。從表中還可以發現，損耗角不隨應變幅值增加而變化，意味著推進劑的阻尼損耗僅對頻率敏感，隨著頻率的增大而增大。

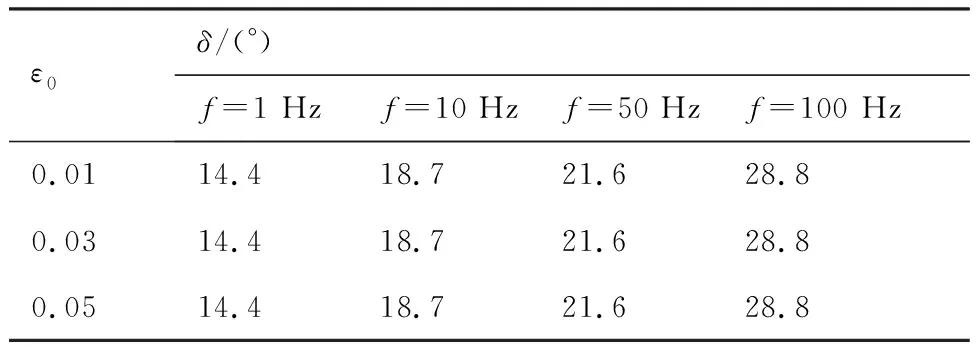
表2 損耗角隨應變幅值和頻率的變化

3.2 能量耗散密度與穩態溫升

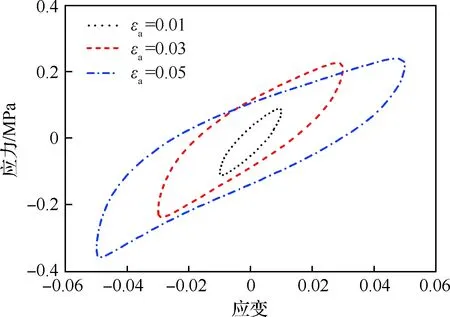
圖5 不同應變幅值下的滯回圈(f=10 Hz)Fig.5 Hysteresis loops at different strain amplitudes (f=10 Hz)

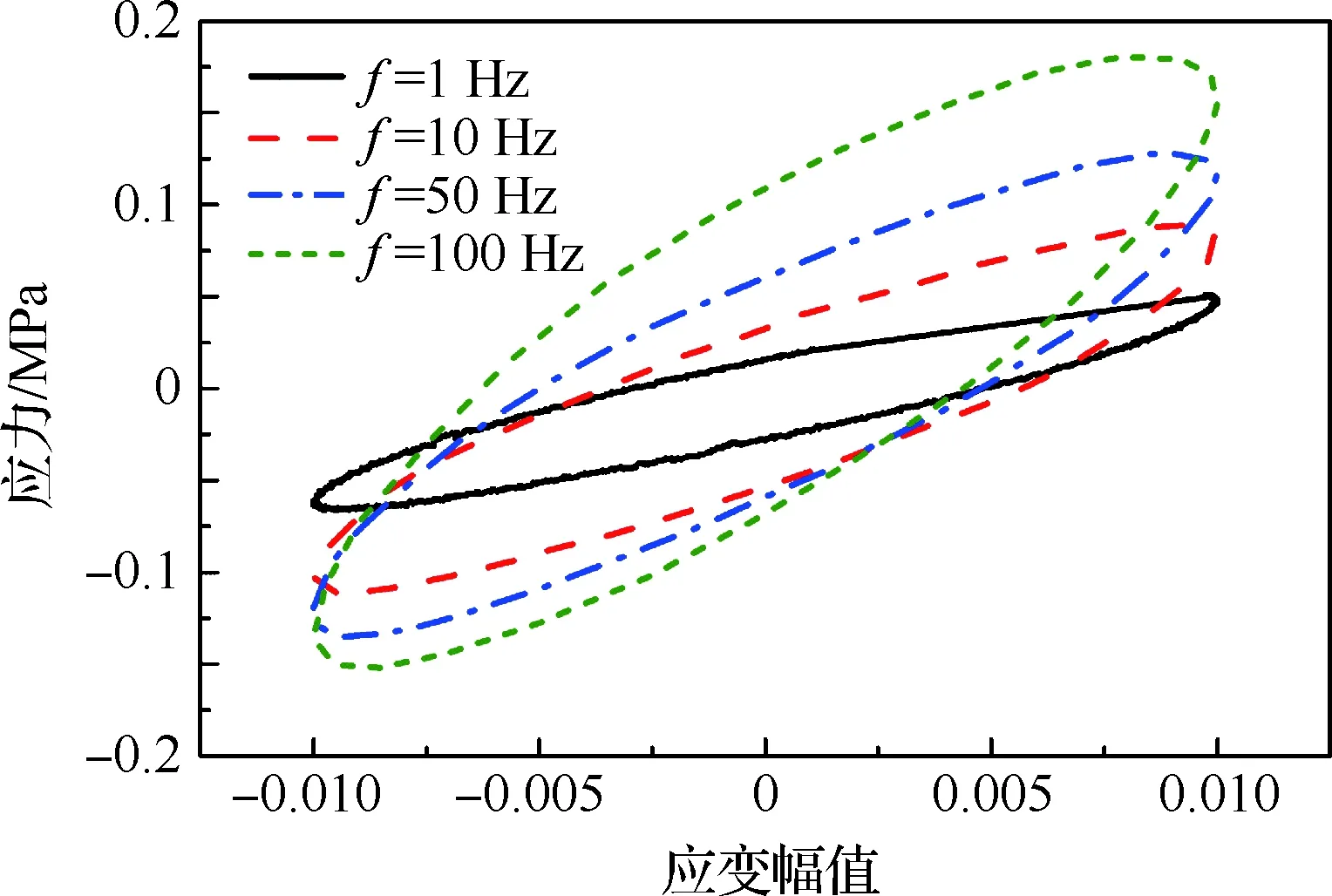
圖6 不同頻率下的滯回圈(εa=0.01)Fig.6 Hysteresis loops at different frequencies (εa=0.01)

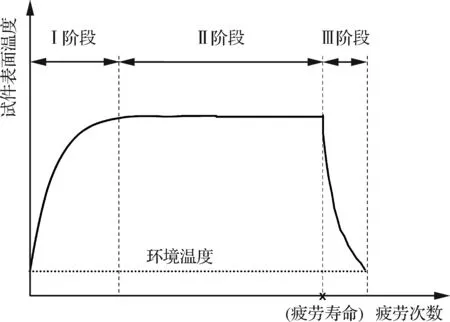
圖7 典型溫度變化曲線Fig.7 Typical curve of temperature variation

圖7給出了HTPB推進劑試件在疲勞加載過程中的典型溫度變化曲線，根據其變化趨勢可以分為3個階段。Ⅰ階段為初始溫升階段：疲勞實驗開始，隨著循環次數的增加，推進劑釋放大量的熱量，實驗開始時試件和環境的溫差較小，對流過程中熱量損失也比較少，試件表面產熱速率大于試件和環境的熱交換率。因此，試件表面溫度快速升高。Ⅱ階段為持續時間最長的溫度穩定階段：隨著疲勞次數的增加，試件表面溫度與環境溫度通過與空氣對流、輻射而平衡下來，當循環載荷下試件釋放的熱量等于散失的熱量時，試件表面產熱速率與試件和環境的熱量交換速率達到平衡，溫度變化達到相對穩定的狀態，僅在小范圍內波動。Ⅲ階段為溫度逐漸降低階段：當試件開始出現裂紋時，達到使用壽命的終點，試件內部不再存在穩定的內熱源，由于試件與環境的對流換熱及與夾具間的熱傳導，試件表面溫度逐漸下降，最終冷卻至環境溫度。

根據熱力學第一定律，并假定推進劑疲勞過程中內部不存儲能量[21](機械能100%轉化為熱能)，則有：

(7)

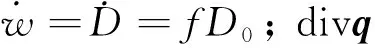
(8)

式中：ΔTS為穩態溫升；NS為溫度達到穩態時的疲勞次數。式(8)為與外界絕熱條件下推進劑能量耗散與穩態溫升的關系。由于D0反映了滯回圈的面積，所以溫升與頻率、應變幅值呈正相關關系。

3.3 溫升的影響因素

材料在循環載荷下自身溫度的升高與內熱源的分布與強度、材料的熱物性參數(導熱系數、比熱容等)以及熱交換環境(對流、輻射)等相關，其中起決定作用的是變形引起的內熱源產熱量，影響最大的因素是載荷頻率與應變幅值[22]。圖8給出了不同頻率和應變幅值下Ⅱ階段的穩態溫升值，可知增大加載頻率和應變幅值的同時，試件的穩態溫升也隨之增加。擬合可得穩態溫升值ΔTS與應變幅值εa和頻率f之間的關系為

ΔTS=-0.913+12.166εaf

(9)

即ΔTS∝εaf，相關系數R2=0.99。在圖9中，將預測結果與文獻[4]在f=100 Hz、εa∈[0.01, 0.05]下的實驗值進行對比，驗證了式(9)的正確性。

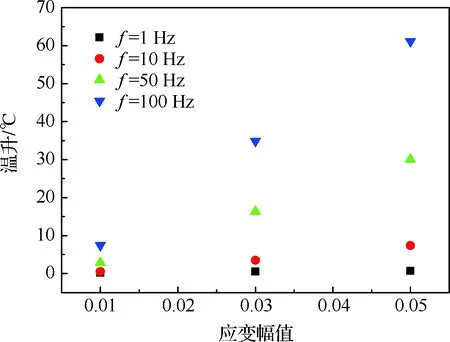
圖8 不同頻率下的穩態溫升Fig.8 Stable temperature rise at different frequencies

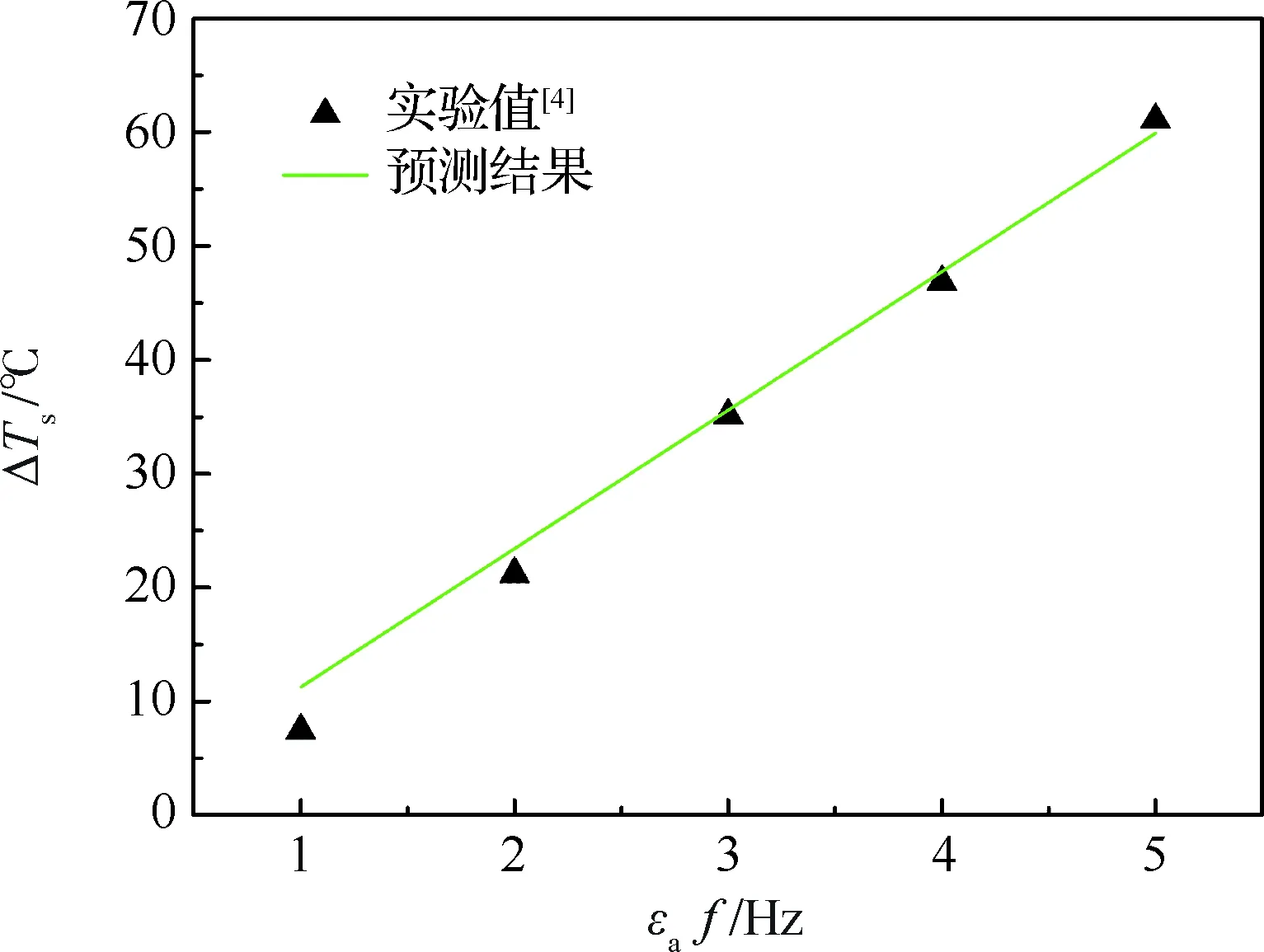
圖9 預測溫升與實驗值的對比Fig.9 Comparison of predicted and experimental temperature rise

4 滯后溫升的計算

4.1 溫度場函數

圖10為長方體試件的示意圖，兩端面邊長均為2a，試件高度為b。試件上下兩端面與剛性平板連接，假設連接面無摩擦，且剛性平板絕熱。由于黏彈性滯后效應引起了材料產熱，相當于在材料內部形成了內熱源，將HTPB推進劑視為各向同性材料，則上述兩端絕熱的矩形體的溫度場控制方程為

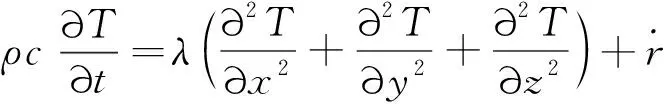
(10)

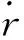
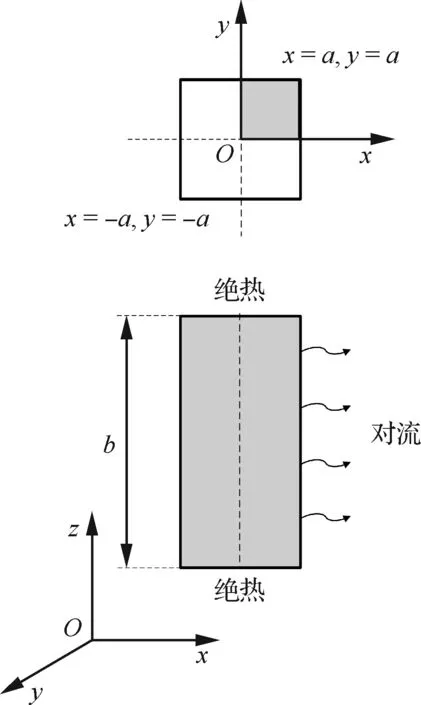
圖10 計算模型示意圖Fig.10 Schematic of calculated model

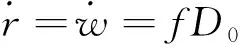
(11)

考慮第3類邊界條件和試件的對稱性，得到三維、非穩態、常物性、有內熱源的導熱微分方程:

(12)

式中：h為復合推進劑與空氣的對流換熱系數；T∞為環境溫度; 0≤x≤a, 0≤y≤a, 0≤z≤b。

4.2 計算結果分析

數值仿真軟件COMSOL Multiphysics通過求解偏微分方程組(多物理場)來實現真實物理現象的仿真[23]，在多物理場耦合計算方面具有很大的優勢和可靠性。由于直接求解式(12)較為困難，因此利用COMSOL Multiphysics進行了仿真計算。

根據實驗建立一個三維長方體模型，試件的材料屬性見表1，邊界條件如圖10所示，計算區域為界面為5 mm×5 mm、高度為15 mm的長方體，上下邊界絕熱，4個側面與外部空氣為自然對流，環境溫度為23 ℃。網格設置為物理場控制網格，單元尺寸為常規尺寸。

圖11為t=83 s試件的溫度云圖，其中內熱源強度為1×106W/m3(對應的加載參數為f=100 Hz，εa=0.05)。從圖中可發現，長方體的中心區域與外圍存在顯著的溫度梯度，而高度方向(z軸)的溫度梯度很小。由于空氣的持續冷卻作用，外側面溫度偏低。

圖12(a)為圖11中z=7.5 mm截面的放大圖，可進一步觀察到，隨著區域的增大，內部熱流逐漸向外部作用，等溫線的形狀接近試件的上側面輪廓。同樣地，在圖12(b)可明確x或y方向上熱源由內向外擴散。

為了與實驗環節所得的試件表面溫升進行比較，提取了仿真結果中的溫度數據(仿真時設定內熱源的大小與實驗中的穩態內熱源強度一致，對應加載的不同應變幅值和頻率)，對比結果如圖13所示，圖中實線為仿真結果，空心符號為實驗結果。實驗值與仿真結果誤差較小，可預測不同加載條件下的試件表面溫度演化情況。同樣，仿真結果也揭示出內熱源恒定的假設對計算結果的影響較小，因此假設較為合理，可以極大地提高計算效率。

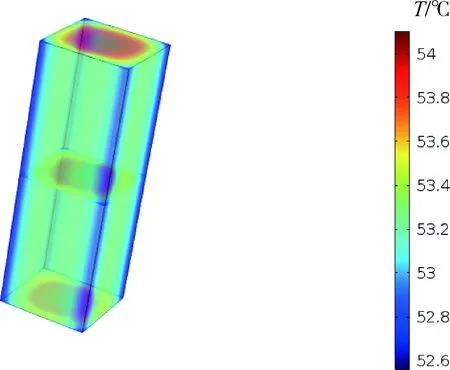
圖11 t=83 s時試件的溫度云圖Fig.11 Temperature nephogram of specimen at t=83 s

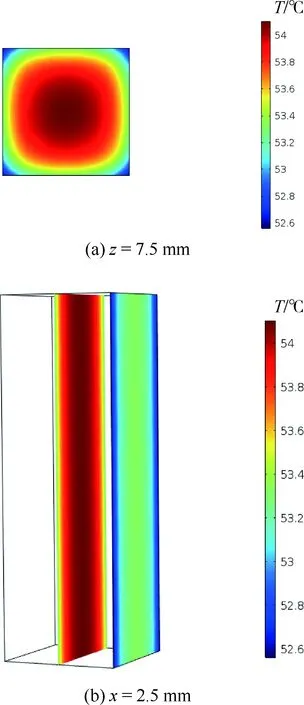
圖12 不同截面處的溫度云圖Fig.12 Temperature nephogram of different cross- sections

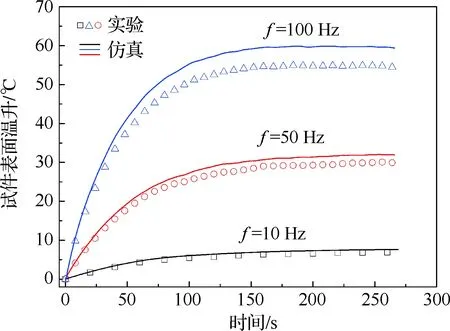
圖13 試件表面溫升仿真與實驗結果對比(εa=0.5)Fig.13 Comparison of surface temperature rise of specimen between simulated and experimental results (εa=0.5)

5 結 論

針對復合推進劑在循環載荷下的能量耗散及其滯后溫升問題，進行了實驗和理論分析，得到以下結論：

1) 應變控制模式下，復合推進劑疲勞中的能量耗散主要受加載頻率和應變幅值影響，能量耗散導致的試件表面溫升最高可達61 ℃(加載條件為εa=0.05,f=100 Hz)。

2) 復合推進劑受循環載荷時，推進劑表面穩態溫升值ΔTS與加載的應變幅值εa、頻率f的乘積εaf呈正比關系，即：ΔTS∝εaf。

3) 通過對三維模型的有限元仿真，假定內熱源恒定，得到了滯后溫升的計算結果，與實驗值較為吻合，可預測不同加載條件下的溫升值。