用于薄片試樣彈塑性應力-應變分析的半解析方法

劉勤，蔡力勛，陳輝

西南交通大學 力學與工程學院，成都 610031

在航空、核電、微機械等關鍵工程領域中，結構零部件經受溫度、壓力等單向或循環載荷作用，材料的單調與循環力學性能對于材料與結構的安全評價具有重要意義[1-2]。新材料研制、結構小型化會因材料尺寸限制，采用傳統大尺寸試樣的試驗方法難以滿足材料性能測試的需求[3-4]。開展以毫米厚度薄片小試樣獲取材料的力學性能測試方法創新研究有重要意義。

通過小試樣獲取材料的力學性能已有不少研究。對于傳統構型的小試樣常用單軸拉伸試驗獲取材料性能，其中Liu等[5]研究尺寸效應對焊接材料的影響，完成了不同厚度的等直片狀試樣單軸拉伸試驗，并用數字圖像相關(Digital Image Correlation,DIC)技術測量獲取載荷與局部應變關系；Gussev[6]和Liu[7]等考慮到輻照裝置的體積制約和樣品放射性的嚴格限制，設計了厚度為0.2 mm、長度為2 mm的“狗骨型”試樣，獲取核反應堆材料的單調應力-應變關系。而對于非常規構型小試樣，常省去試樣夾持段，通過壓縮或者壓入的方式加載，其中Nemat-Alla[8]、Reddy和Reid[9]為研究圓管材料的軸向或環向的力學性能，分別采用軸壓或側壓管試樣的方法獲取材料兩個方向應力-應變關系；為得到在役核電材料力學性能，Manahan等[10]提出了小沖桿的試驗方法平壓小圓片試樣；Cheng[11]通過剛性壓頭壓入被測材料實現了材料單軸本構關系的獲取。但這些壓力加載的方法通常依賴于有限元回歸，難于能給出較為簡單的解析描述。循環應力幅-應變幅曲線是表示循環變形下材料變形抗力的重要特性，定義為循環變形達到穩定狀態時，連接各應變幅下應力-應變滯回曲線頂端的曲線。傳統試驗方案采用標準試樣[12]在多級應變幅下的軸向等幅對稱循環試驗獲取。為研究鋁薄膜和銅薄膜的疲勞性能，Read[13-14]等設計完成了“啞鈴”狀薄片試樣的拉-拉疲勞試驗，該試驗方案能較好地測試在受拉的柔性構件力學性能，但并不能通過該試樣獲取材料對稱低循環應力-應變關系。Melander等[15-17]設計了厚度為1.4 mm、長寬比小于2的等直板試樣完成軸向應變控制的拉壓循環試驗，試驗的應變幅限制在0.25%內以避免失穩，因而未獲得較大應變范圍的循環應力-應變關系。既為了防止薄板試樣失穩又保證足夠的應變幅范圍，Martin[18]和Wisner等[19]采用圓弧漏斗試樣開展對稱循環試驗，分別利用厚度方向與寬度方向的應變進行循環控制，以漏斗最小橫截面的平均彈性應變幅與修正的等效塑性應變幅之和作為軸向應變幅，并以該截面的平均應力作為軸向應力幅，建立材料的循環應力幅-應變幅關系。賈琦等[20-21]針對具有循環Masing效應的特定材料，提出了取等直圓棒試樣最大應變幅穩定階段應力-應變滯回環上升段作為材料的循環本構關系，但未給出通過漏斗薄片試樣來獲取材料的循環本構關系的方法。尹濤等[22-23]完成了毫米厚的漏斗薄片試樣的低周疲勞試驗設計，通過建立能量分離函數原創地提出了預測循環應力幅-應變幅關系的半解析方程，該方法所采用的方程較為復雜，局限于具有幾何相似性的漏斗薄片試樣。

本文作者[24-27]提出了Chen-Cai能量等效方法，給出了該方法的理論推導，并根據錐壓和圓環側壓以及沖壓試驗獲取材料應力-應變關系。本文基于Chen-Cai能量等效方法，針對圓弧漏斗薄片試樣和圓環薄片試樣，提出獲取材料應力-應變關系的載荷-位移統一模型，通過單軸拉伸試驗和變幅循環試驗獲得材料應力-應變關系與循環應力-應變關系。

1 載荷-位移關系統一模型

假定試樣材料連續、均勻、各向同性、等向強化，采用Ramberg-Osgood冪律模型描述單調加載下的材料應力-應變關系，即

(1)

式中：ε、εe和εp分別為總應變、彈性應變和塑性應變；σ為應力；E為彈性模量；K為應力強度系數；n為應變硬化指數。

對于符合Ramberg-Osgood律的材料，漏斗薄片試樣和圓環薄片試樣的測量位移h可近似表達為彈性位移he與塑性位移hp之和[27],即

h=he+hp

(2)

總應變能可表達為

U=Ue+Up

(3)

式中：Ue為應變能彈性分量;Up為應變能塑性分量。

1.1 彈性應變能模型

在線彈性條件下，漏斗和圓環薄片試樣末端在軸向載荷P作用下產生彈性位移量為he，由量綱相似原理，可以假設變形域內的彈性應變能與軸向位移的平方成正比[28]，則彈性應變能可表為

(4)

式中：k0為彈性系數。假設包含主要變形的規則幾何區域為變形域，用Ω表示，如圖1所示。選取Ω中能代表形狀變化的幾何參量為特征長度，用h*表示，本文中h*選為圓弧漏斗試樣的缺口半徑及圓環薄片試樣外半徑R；變形域的特征體積用V*表示，V*=h*A*；A*表示特征面積，對漏斗試樣A*=(2w-πR)t，w為工作段寬度，t為試樣厚度;對圓環薄片試樣，A*=π(R2-r2)t/R，r為試樣內半徑。如圖1所示的漏斗和圓環薄片試樣工作段幾何構形，加載線的A端為固定端，B端采用位移加載。

在準靜態下，載荷做功不考慮熱耗散，則

(5)

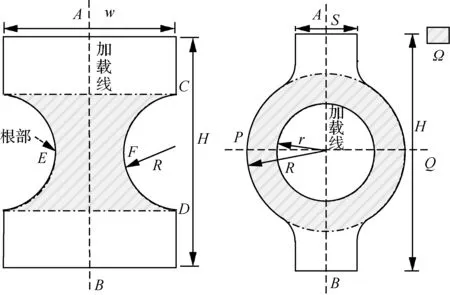
圖1 漏斗薄片試樣與圓環薄片試樣工作段構形圖Fig.1 Configuration of working sections of sheet-funnel specimen and sheet-ring spcimen

式中：We為載荷P作用下所做的彈性功。對式(5)求導

(6)

結合式(4)和式(6)，可得彈性條件下載荷-位移關系為

(7)

式中：彈性系數k0為與試樣構形幾何尺寸相關的函數，試樣構形用幾何因子λ表示，且λ=w/R。經過基于有限元方法的簡單分析可知，彈性系數與幾何因子滿足拋物律關系,即

k0=a1λ2+a2λ+a3

(8)

其中：a1、a2、a3為待定常數。

1.2 塑性應變能模型

假設材料本構關系符合Ramberg-Osgood關系式(1)中的塑性分量式，即εp=(σ/K)n。變形域內任一點坐標可以用(x,y,z)表示，那么該點所在材料代表性單元(Representative Volume Element, RVE)的應變能密度記為u(x,y,z)，則Ω域的塑性應變能可表示為

(9)

式中：up為試樣的塑性應變能密度。根據Chen-Cai能量等效方法[24]，能量中心的點(xm,ym,zm)處RVE的塑性應變能密度upm可表示為

(10)

則式(9)所示的Ω域內的塑性應變能Up可簡單表示為

(11)

若以體積系數k1表示Ω域體積V與特征體積V*的比值，即

(12)

并假定等效塑性應變εp-eq與無量綱塑性位移hp/h*符合線性關系

(13)

式中：k2為塑性應變系數，將式(12)和式(13)代入式(11)，塑性應變能Up與無量綱塑性位移hp/h*滿足以下關系

(14)

假設Wp為載荷P作用下的塑性功，在不考慮加載熱損失的情況下

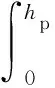
(15)

由式(14)和式(15)及V*=h*A*，可得P與hp之間的關系式為

(16)

進一步簡化為

(17)

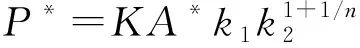
(18)

式中：b1、b2、b3、c1、c2、c3為待定常數。

1.3 載荷-位移統一模型

結合式(2)、式(7)和式(19)，整理可得漏斗和圓環薄片試樣的載荷-位移統一模型

(19)

式中：k與材料常數(K，n)、彈性模量E和幾何因子λ有關;P*與彈性幾何因子λ、漏斗和圓環薄片試樣半徑R和材料常數K有關。漏斗薄片試樣幾何因子λ=w/R，且λ∈(2.75，4)；對于圓環薄片試樣，λ=r/R，且λ∈(0.48，0.72)，并定義圓環薄片試樣拉伸連接段工作帶寬度為S，S=4(R-r)，過渡圓弧半徑rt=r/4。

由于試樣的厚度方向尺寸遠小于長度、寬度方向，基本符合平面應力假設，有限元計算采用帶厚度的Plane183平面應力單元進行計算，單元最小尺寸為1 μm，共2 500個單元。將該模型上端固定，下端采用位移加載，加載位移為0.1 mm。

鑒于模型的無量綱特性，設定彈性模量為E=200 GPa，采用有限元平面應力模型進行簡單的純彈性計算，即根據式(7)可確定彈性系數k0。如取he為漏斗薄片試樣的加載線上彈性位移，則k0隨λ的變化規律如圖2(a)所示，可得a1、a2、a3分別為0、-0.009 74、0.092 6。為了測量方便，如Wisner等[19]，也常選取漏斗試樣橫向位移計算，系數k0與泊松比υ有關，所以k0/υ與λ的變化規律如圖2(b)所示，從而確定了參數a1、a2、a3的取值分別為-0.002 06υ、0.001 15υ、0.012 2υ。

擬定強度系數K=1 000 MPa，硬化指數n=5，采用純塑性計算確定體積系數k1和塑性應變系數k2，同樣選取漏斗試樣加載線位移可得式(18)中b1、b2、b3及c1、c2、c3的值，如圖3所示。

事實上，如圖1所示的加載線(A-B)位移對載荷引起的非線性敏感性弱，根據實際試驗測量條件，往往采用跨漏斗圓弧兩側(C-D)位移和漏斗腰部橫向(E-F)位移作為測量目標。對于圓環薄片試樣的加載線(A-B)位移和圓環橫向(P-Q)位移，根據有限元計算確定系數k0、k1、k2，所以兩種試樣的系數參數如表1所示。

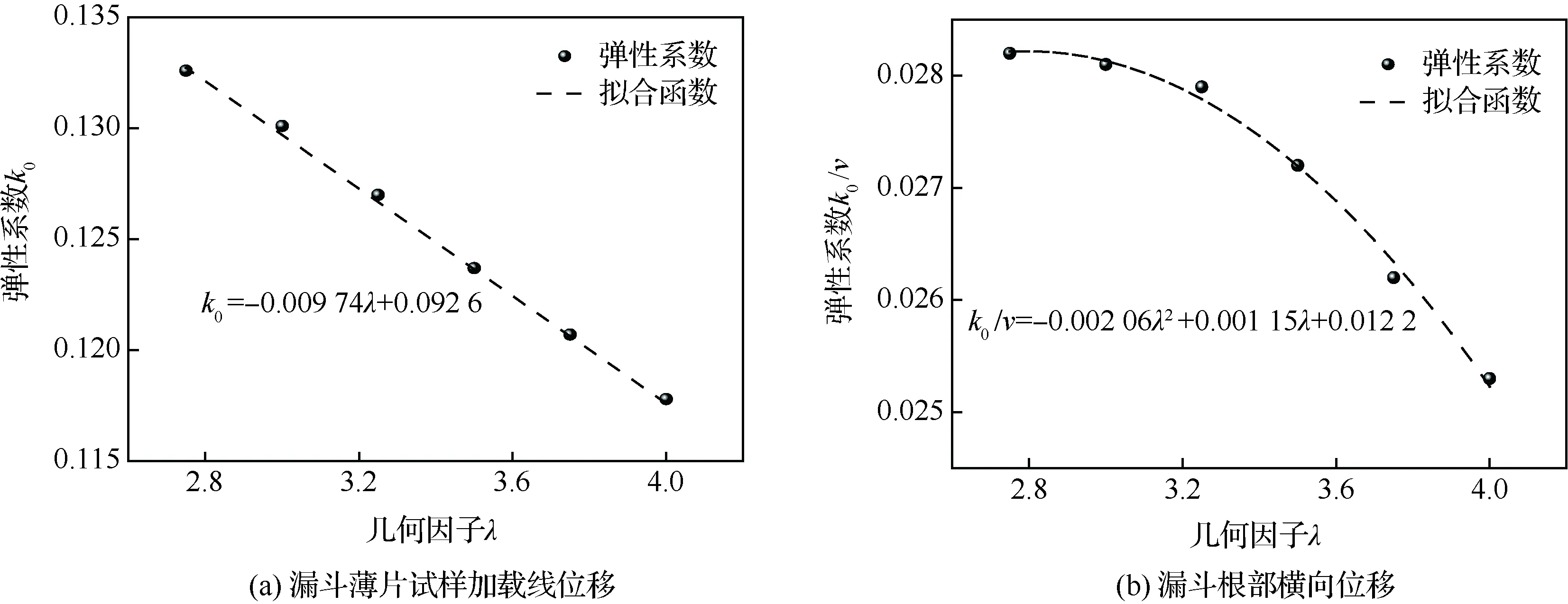
圖2 彈性系數k0、k0/υ與幾何因子λ的關系曲線Fig.2 Relation between elastic coefficient k0, k0/υ and geometric factor λ

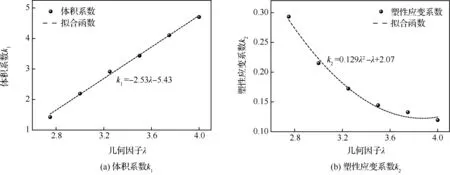
圖3 系數k1、k2與幾何因子λ的關系曲線Fig.3 Relation curves of coefficient k1, k2and geometric factor λ

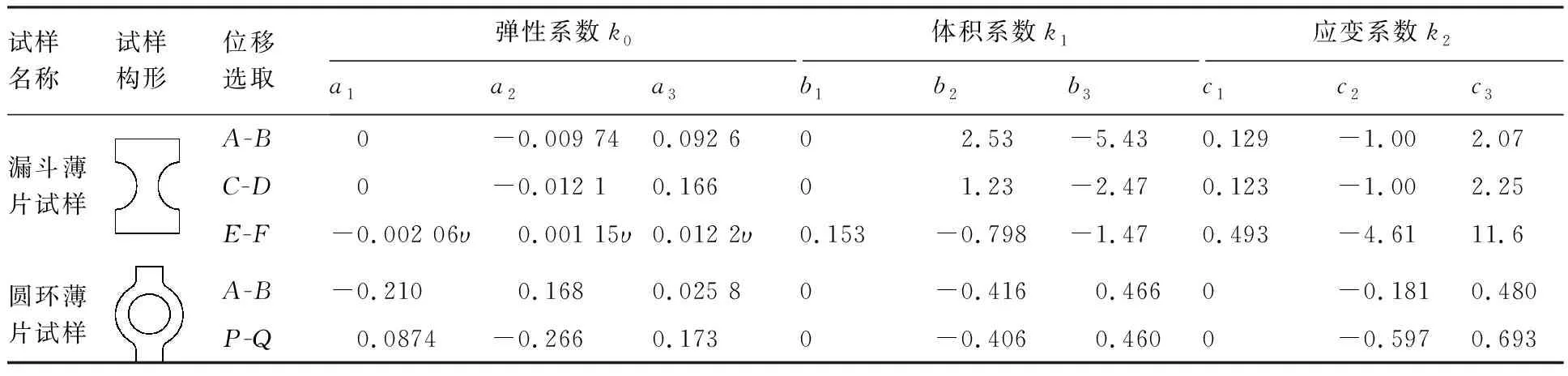
表1 統一模型參數Table 1 Parameters of unified model

2 有限元驗證

根據式(19)統一模型，定義應力-應變關系預測載荷-位移響應為正向預測，已知載荷-位移關系求材料應力-應變關系為反向預測。

2.1 正向預測驗證

由于工程測試中，跨漏斗兩側位移比較方便測量，本文先取漏斗薄片試樣的跨漏斗兩側位移進行驗證。任選取一組試樣的幾何形狀和材料屬性進行有限元計算，如取試樣缺口半徑R=2 mm、彈性模量E為150～220 GPa、材料強度系數K為100～3000 MPa、塑性硬化指數n為2～20。簡單計算可以得到對應的載荷-位移關系，稱之為FEA(Finite Element Analysis)載荷-位移關系；通過統一模型也可預測出對應的載荷-位移關系，稱為模型預測載荷-位移關系，經無量綱處理后的FEA載荷-位移關系曲線與模型預測載荷-位移關系曲線如圖4所示，圖4(a)～圖4(d)分別表示變化不同參數的預測結果。

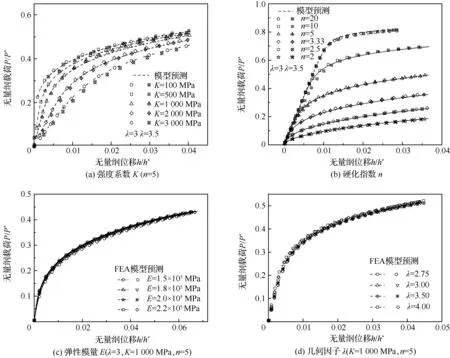
圖4 漏斗薄片試樣的P/P*-h/h*模型曲線與FEA計算曲線的對比Fig.4 Comparison of P/P*-h/h* model and FEA calculation curves of sheet-funnel specimen

經正向驗證，模型預測的漏斗薄片試樣P/P*-h/h*曲線與FEA計算曲線的結果基本一致。其中圖4(a)對比了兩種試樣、同彈性模量、同硬化指數的前提下，改變強化系數的結果，強化系數越大，無量綱載荷越大；圖4(b)為僅改變硬化指數，硬化指數越大，無量綱載荷越大；圖4(c)僅變化彈性模量，分散性較小，彈性模量對P/P*-h/h*曲線的走勢影響較小；在同一材料參數下，改變幾何因子，如圖4(d)所示，不同λ的P/P*-h/h*曲線吻合良好，表明模型預測曲線只與材料屬性有關。所以在選取漏斗薄片試樣的其他位移驗證時，主要考慮材料塑性屬性對曲線的影響，假定E=200 GPa、λ=3，驗證當K=500、1 000 MPa時，不同硬化指數n對漏斗薄片試樣加載線位移和漏斗根部橫向塑性位移的P/P*-hp/h*曲線影響，如圖5所示。

圖5對比了薄片試樣加載線位移和漏斗根部橫向下的強度系數與同硬化指數對P/P*-hp/h*曲線影響。同硬化指數、不同強化系數的FEA計算曲線均能重合于同一條模型預測曲線；硬化指數越大，曲線走勢越高。同時圖5(b)顯示，當選取漏斗根部橫向位移時的預測結果并不敏感，且硬化指數較大時，預測結果偏差很大，所以硬化強度低的材料不適于測量漏斗試樣橫向位移進行試驗。

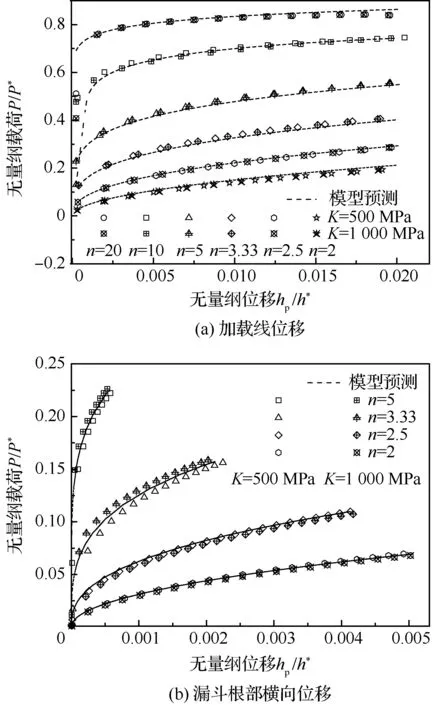
圖5 漏斗薄片試樣的P/P*-hp/h*模型曲線與FEA計算曲線的對比Fig.5 Comparison of P/P*-hp/h*model and FEA calculation curve of sheet funnel-specimen

根據漏斗試樣驗證結果，只需計算材料的不同硬化指數n對圓環薄片試樣模型預測與FEA計算的P/P*-hp/h*曲線的影響，如圖6所示，即完成統一模型正向驗證。

經有限元計算的正向預測結果表明：統一模型理論預測對漏斗薄片試樣與圓環薄片試樣的不同位置位移均適用，且在同一選取的位移尺度下的P/P*-h/h*曲線只與材料屬性有關。

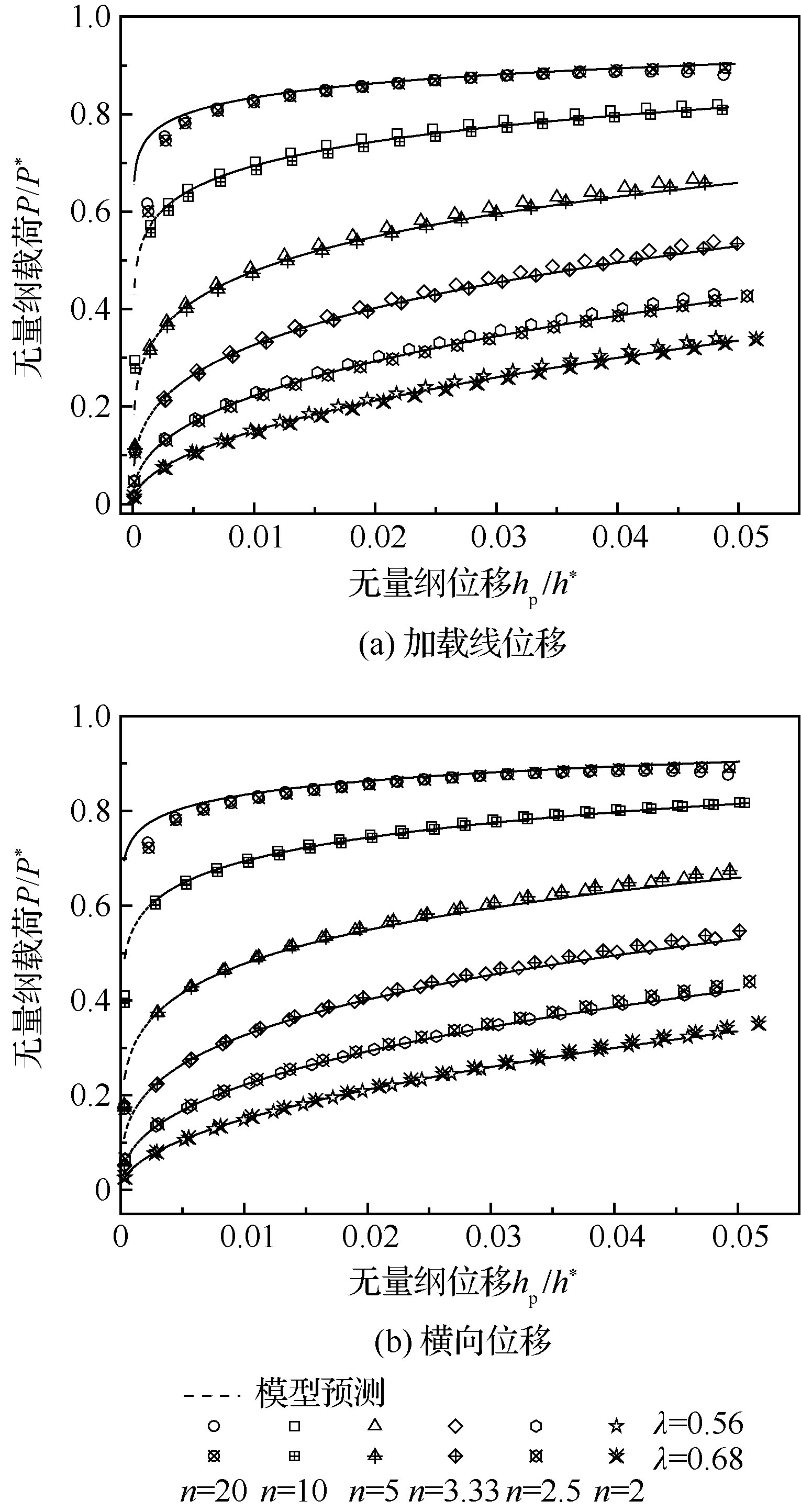
圖6 圓環薄片試樣模型預測與FEA計算的P/P*-hp/h*曲線對比Fig.6 Comparison of P/P*-hp/h* curves between model prediction and FEA calculation of sheet-ring specimen

2.2 反向預測驗證

選取合適的Ramberg-Osgood模型參數(E，K,n)組合，經簡單有限元計算獲取載荷P與漏斗兩側位移hf的關系。對P-h關系曲線的線性段用函數P=ηhe擬合，η表示直線段斜率，由式(7)得到該材料的彈性模量E。根據hp=h-he可得到P-hp曲線，用函數P=P*(hp)m擬合P-hp曲線，可由式(17)得到該材料的塑性參量強度系數K、硬化指數n，應力-應變關系參數為

(20)

根據式(20)所得的參數代入式(1)，由載荷-位移關系反向預測應力-應變關系。選取跨漏斗薄片試樣兩側的位移，針對不同材料屬性、不同幾何因子完成理論模型預測。輸入彈塑性應力-應變關系，經有限元計算得到載荷-位移關系，通過該載荷-位移關系經模型反向預測的應力-應變關系，并將其與輸入FEA的應力-應變曲線進行比較，如圖7所示，圖7(a)～圖7(d)表示不同參數對比結果。

經過反向預測比較，統一模型的預測應力-應變曲線與FEA計算輸入曲線基本一致。圖7(a)和圖7(b)分別對比了不同強度系數K和硬化指數n的模型預測應力-應變關系曲線，與FEA輸入應力-應變曲線對比結果，K越大曲線趨勢越高，n越大曲線越高，且曲線后半段越平；不同彈性模量的曲線分散性小，如圖7(c)所示，彈性模量E對模型預測應力-應變關系的影響較小；圖7(d)顯示同一材料屬性、不同幾何構型反向預測的應力-應變曲線，均能重合與同一FEA應力-應變曲線，反向預測結果與幾何因子無關。

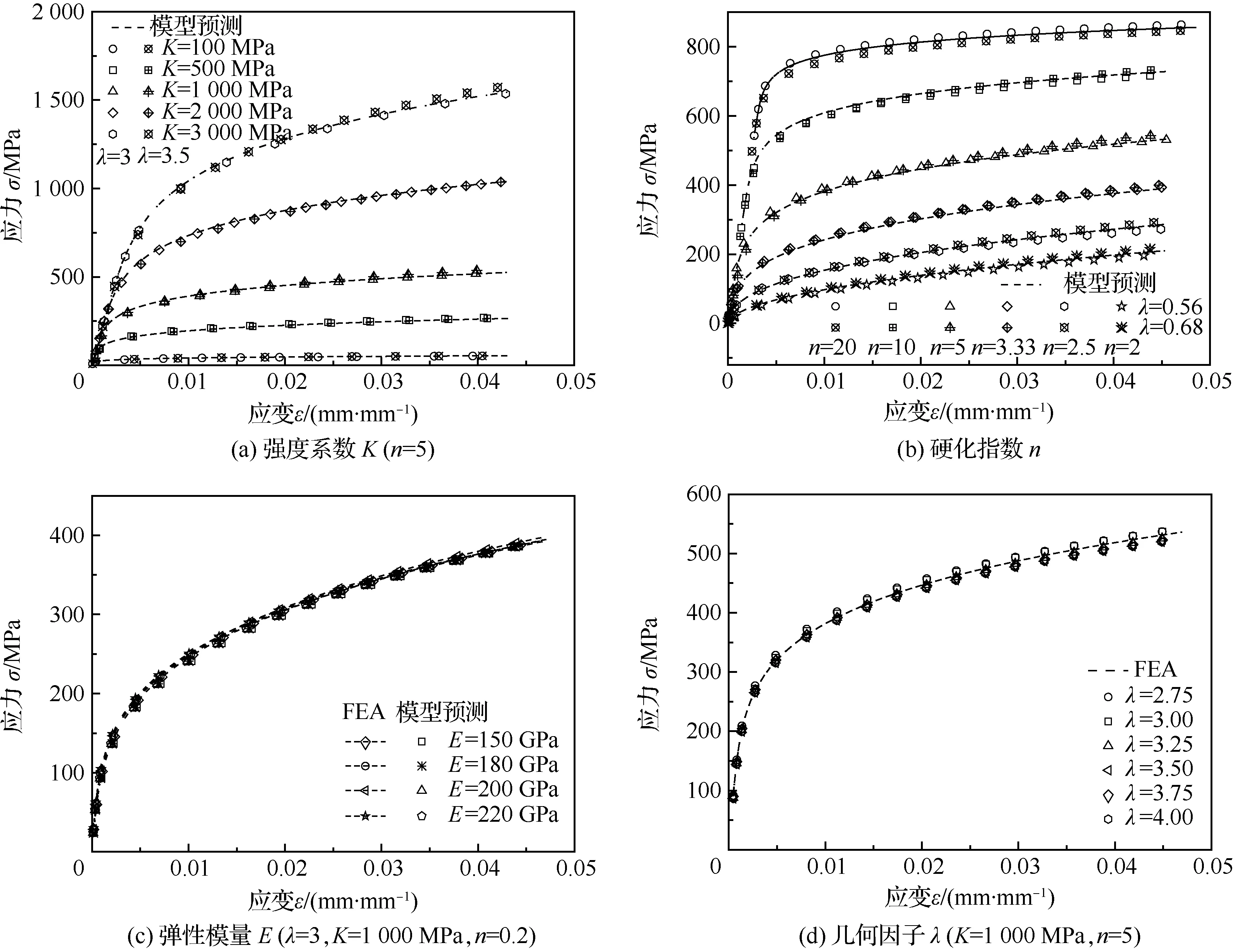
圖7 漏斗薄片試樣模型預測σ-ε曲線與FEA計算輸入曲線對比Fig.7 Comparison of σ-ε model and FEA calculation curves of sheet-funnel specimen

為對比不同試樣構形與不同位移選取的應力-應變關系預測結果，其中包括漏斗薄片試樣的跨漏斗兩側軸向位移、加載線位移與薄片圓環的加載線位移、圓環橫向位移。對相同材料屬性完成對上述的不同位移的預測，如圖8所示，是選取彈性模量E=200 GPa、強度系數K=1 000 MPa與硬化指數n=5時的預測結果。

采用不同試樣構形及位移反向預測的應力-應變曲線與FEA應力-應變曲線基本一致，所以采用漏斗薄片試樣的跨漏斗兩側軸向位移、加載線位移與薄片圓環的加載線位移、圓環橫向位移均能準確預測材料的應力-應變關系。

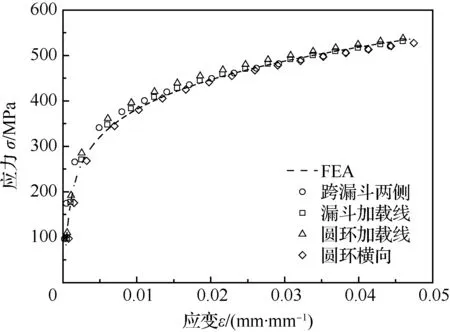
圖8 不同的試樣構形模型預測σ-ε曲線與FEA計算輸入曲線對比(K=1 000 MPa)Fig.8 Comparison of predictions of σ-ε and FEA calculation input curves by different configurations (K=1 000 MPa)

3 試驗與結果

3.1 試驗條件

GH4169是一種新型高溫合金材料，對應進口材料美國牌號為Inconel 718，主要成分: Ni 50%～55%、Cr 17%～21%、Nb 5%～5.5%、Mo 2.8%～3.3%、Ti 0.75%～1.15%、Co ≤1%、Mn ≤0.35%、Si ≤0.35%、 Cu ≤0.3%。由于其強度高、耐高溫、并有較好延性，且具有良好的高溫強度、加工硬化性及焊接性，在航空工程飛機葉片及核電工程密封環等關鍵領域中應用廣泛。

設計漏斗薄片試樣與圓環薄片試樣如圖9所示，試樣尺寸為元幣大小，設計長度H=24 mm、總寬度L=10 mm、厚度t=0.5 mm，兩端夾持，中間為工作段，其寬度w=3.6 mm、圓弧漏斗半徑R=1.2 mm，而圓環薄片試樣外徑R=2.5 mm、內徑r=1.7 mm、工作段寬度S=3.2 mm、過渡圓弧半徑rt=1 mm。

圖9 薄片試樣構形圖Fig.9 Shape diagram of thin slice specimen

薄片試樣的對稱循環試驗是采用Care IBTC-300原位雙向拉壓疲勞試驗機完成的，設備的載荷量程1 kN；利用632.29F-30 引伸計實現了軸向應變測控，其標距為5 mm，測量范圍-10%～30%，試樣及引伸計裝置如圖10所示。單軸拉伸速率為0.001 mm·s-1，變幅循環試驗采用控制應變幅自低到高分級加載，每500微應變為一級，每級應變幅下分別循環100周，加載波形為三角波，加載速率為0.002 mm·mm-1·s-1。

采用直徑為4 mm的等直圓棒試樣作為比對試樣，單軸拉伸試樣等直段為32 mm，疲勞試樣等直段長8 mm。采用美國MTS 809電液伺服材料試驗機，載荷量程為250 kN,控制系統為TestStarⅡ，應用軟件為MTS790.10/SX，引伸計采用MTS 632.29F-30(標距為5 mm，測量范圍-10%～30%)實現軸向應變控制。

圖10 圓環薄片試樣試驗裝置圖Fig.10 Test device for sheet-ring specimen

3.2 材料應力-應變獲取

完成單軸拉伸試驗，分別測量跨漏斗試樣兩側位移和圓環試樣外的加載線位移，并獲取兩種試樣的載荷-位移曲線如圖11所示。

根據以上兩種試樣的載荷-位移曲線，經反向預測可以獲取應力-應變曲線，與比對試樣比較結果如圖12所示。

比較圖12，經漏斗薄片試樣與圓環薄片試樣預測的單軸應力-應變關系與對比試樣試驗結果基本重合。根據圖12可以得到，材料彈性模量E=204 GPa，采用Ramberg-Osgood本構模型描述得到強度系數K=1 540 MPa、硬化指數n=18.1。

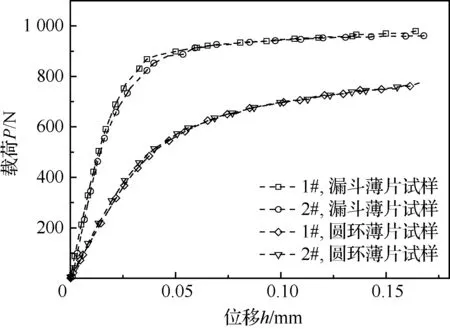
圖11 漏斗薄片試樣和圓環薄片試樣載荷-位移曲線Fig.11 Load-displacement curves of sheet-funnel specimen and sheet-ring specimen

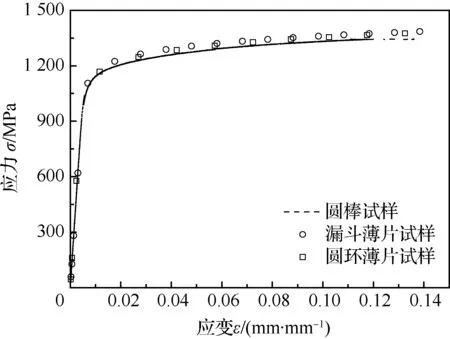
圖12 單軸拉伸應力-應變關系曲線Fig.12 Stress-strain relation curve of uniaxial tension

3.3 循環應力-應變關系預測

完成了漏斗薄片試樣與圓環薄片試樣及對比試樣的增幅循環試驗，取每級循環中間次數的穩定載荷-位移曲線為載荷-位移滯回環曲線，連接各級滯回曲線尖點為循環載荷-位移曲線，漏斗薄片試樣與圓環薄片試樣的循環載荷-位移曲線如圖13所示。

獲取等直試樣的循環應力-應變滯回曲線,定義最大應變回環的上升段為循環應力-應變特征曲線,如圖14所示。

根據圖14顯示，特征曲線基本過應力-應變滯回曲線尖點，該材料大致符合Masing效應。漏斗薄片試樣與圓環薄片試樣的循環載荷-位移曲線，并與對比試樣的循環應力-應變曲線和單軸應力-應變曲線比對如圖15所示。

比較圖15的循環應力-應變曲線，反向預測漏斗薄片試樣與圓環薄片試樣的循環應力-應變曲線與比對試樣的循環應力-應變曲線基本重合，說明在循環載荷下的應力-應變關系是唯一的，與幾何構型無關。材料在循環載荷下的彈性模量E=197 GPa、 強度系數K=1 505 MPa、 硬化指數n=15.2。單軸拉伸應力-應變曲線明顯高于循環應力-應變曲線，GH4169在常溫條件下表現循環軟化特征，而硬化程度稍有增強。

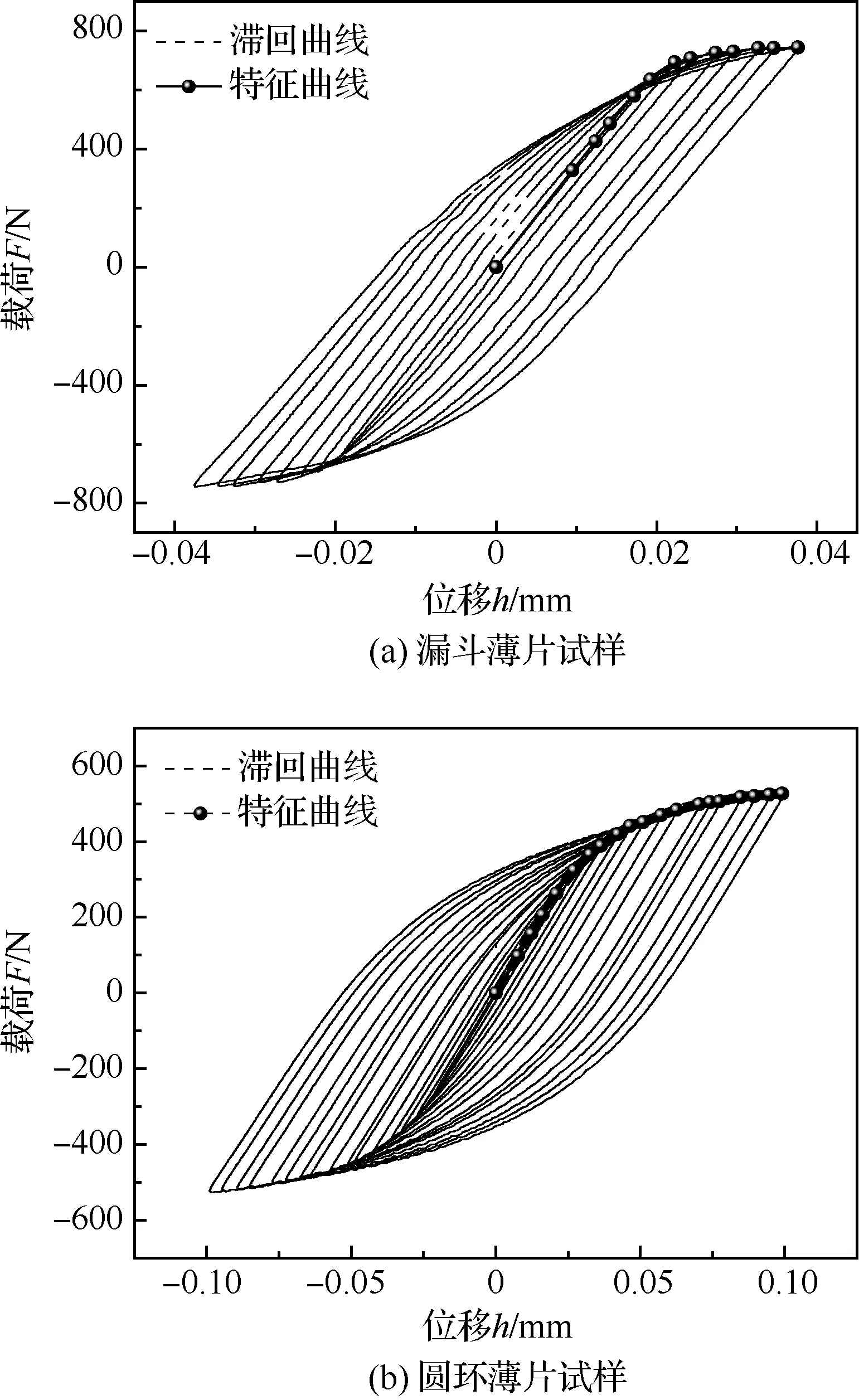
圖13 漏斗薄片試樣與圓環薄片試樣的循環載荷-位移曲線Fig.13 Cyclic load-displacement curves of sheet-funnel specimen and sheet-ring specimen

圖14 對比試樣應力-應變滯回環曲線Fig.14 Curres of stress-strain hysteresis loops of contrast specimens

圖15 循環應力-應變關系和單軸應力-應變關系曲線Fig.15 Relation curves of cyclic stress-strain and uniaxial stress-strain relation

4 結 論

1) 提出了基于漏斗薄片試樣和圓環薄片試樣獲得單調應力-應變關系和符合Masing律材料的循環應力幅、循環應變幅關系的統一模型。

2) 在幾何因子λ∈(2.75，4)范圍內，經有限元正、反向驗證表明，對漏斗薄片試樣不同位移的統一模型均有良好普適性；該模型對λ∈(0.48，0.72)的圓環薄片試樣同樣適用。

3) 經漏斗薄片試樣和圓環薄片試樣獲取的應力-應變關系曲線和循環應力-應變曲線，均與等直試樣在單調載荷下獲取的應力-應變關系和循環加載下的循環應力-應變曲線基本保持一致。

4) 材料循環應力-應變曲線的獲取是完成材料疲勞壽命預測和抗疲勞設計的關鍵，本文統一半解析模型可為實現以毫米級薄片試樣預測低周疲勞壽命提供新方法。