飛行器體系優化設計問題

周健，龔春林，粟華，張孝南，李波，谷良賢

1. 西北工業大學 航天學院 陜西省空天飛行器設計重點實驗室，西安 710072 2. 中國兵器工業第203研究所，西安 710065 3. 洛陽光電設備研究所，洛陽 471023 4. 四川航天系統工程研究所，成都 610100

未來作戰環境復雜易變，戰爭也逐漸轉變為體系之間的對抗，單一武器縱然有卓越的性能，也不再能夠良好地完成作戰任務，武器裝備體系化發展是一個重要的趨勢。武器裝備設計必須要配合體系(SOS)作戰應用環境，不能一味地追求武器性能最優(Measure of Performance，MOP)，而是追求整個武器裝備體系的效能最優(Measure of Effectiveness, MOE)[1]。在設計活動中，除依據設計需求研制武器裝備外，還需考慮其性能指標對體系的影響及其在體系環境中的協同配合。

上述挑戰使得傳統的導彈、飛機等飛行器設計問題變為耦合飛行器設計與體系結構設計的體系優化設計問題。面向體系環境的飛行器設計已得到了較多研究[2-5]。然而，更廣義的體系問題除包含其組成成員的設計外，還包含體系結構的構建，一些學者開始同時考慮體系與飛行器的耦合優化設計問題。Crossley等[6]以假定的航空運輸網絡為研究對象，研究了航線配置與飛機設計耦合問題；Kim和Hidalgo[7]對航空運輸網絡展開研究，并著重考慮了多階段決策問題；Mane等[8]以航空運輸網絡為例，驗證了求解方法對復雜度更高的耦合設計問題的通用性，并進一步考慮了按需航空運營耦合設計問題中的不確定性影響[9-10]；Marwaha和Kokkolaras[11]進一步拓展了航空運輸體系問題規模，除飛機設計與航線配置外，還考慮了運輸網絡的設計；Frommer[12]以搜索任務(Search and Find)與敵方防空火力壓制任務為應用案例，研究了固定翼飛機與變體飛機及其組成機隊的設計和多目標優化問題；Jansen和Perez[13]研究了面向不同市場應用的客機族與航線耦合設計問題；Govindaraju等[14]以減少燃油消耗為目標，考慮了不確定條件下飛機與航線的耦合設計問題；Taylor[15]提出了面向運輸系統的耦合設計方法，并以航空運輸系統和空間運輸系統為例，驗證了方法在提升運輸系統能力方面的有效性；吳煒琦和張育林[16]研究了由偵察衛星、導航衛星和通信衛星組成的天基信息支持系統并獲得了最優衛星與星座設計方案。以上研究表明考慮體系設計和飛行器設計的耦合優化設計能夠進一步提升體系效能。

由于體系結構的復雜性，其求解相比于傳統優化問題也有所不同。Biltgen[3]將體系架構劃分為體系—系統—分系統3層，使得飛行器體系設計問題成為多層次優化問題；Sobieszczanski-sobieski[17]將兩層BLISS-2000[18]嵌套，提出了面向體系優化的三層集成系統綜合(Tri-Level Integrated System Synthesis, TLISS)策略，以適應多層的體系優化問題，但由于計算復雜并沒有具體案例驗證；Kim等[19]提出的多層次(Analytical Target Cascading, ATC)策略為求解體系問題提供可行性，但忽略了優化問題的建模過程；Ayyalasomayajula等[20]基于ATC的思想，提出了一種對體系問題的建模思路，側重于研究成員間的耦合關系及體系演化影響，但對優化過程鮮有提及；Liu等[21]提出了面向體系的飛行器概念設計流程，給出了各步驟中可供借鑒的關鍵技術，但并沒有給出此類問題的通用數學定義，缺乏典型應用案例。上述研究從不同的角度嘗試解決體系設計問題，但并沒有給出其通用的數學定義和建模求解流程，不具備普適性。

本文依據體系工程(SOSE)原理，以導彈類飛行器為研究對象，提出了一類耦合飛行器設計和體系結構設計的飛行器體系優化設計問題，定義了此問題的相關概念和通用數學模型，構建了相應的建模與優化求解流程，并將其應用到巡飛/精打協同武器系統的優化設計。

1 飛行器體系優化設計概念

飛行器和體系結構的優化設計作為獨立學科已開展較多研究[22-23]。對于飛行器優化設計而言，在體系結構假設不變的條件下，依據設計需求開展，由此產生的優化設計問題如式(1)所示。

(1)

式中：xsos和ysos表示輸入的體系結構設計結果，如體系結構設計參數、飛行器設計需求等；xsubsys和ysubsys表示輸入的子系統設計結果，如氣動設計升阻力系數、飛行器質量等；ysys表示其他飛行器系統的影響，代表系統成員間的交互；xsys表示飛行器設計變量；OBJsys為系統層設計目標；gsys和hsys為飛行器設計的不等式和等式約束，優化目標為提升飛行器性能；Fsys為黑箱函數，用于評估飛行器性能，如氣動模型、彈道模型等。

對于體系結構優化設計而言，依據確定的飛行器性能指標與體系需求，對現有飛行器、在研飛行器與待研飛行器進行合理配置和有效集成，最終形成最優體系結構，其優化問題如式(2)所示。

(2)

式中：xsys和ysys表示輸入的飛行器設計結果，如飛行器航程、成本、飛行速度等性能參數；xsos表示體系(結構)設計變量，表征體系組成及其交互關系；OBJsos為體系層設計目標；gsos和hsos為體系設計的不等式和等式約束；優化問題以體系效能最優為目標。體系結構優化設計只考慮體系的頂層設計問題，而不關心單個系統的設計和實現[23]。

實際上，根據體系工程原理[24]和體系工程過程[25]，飛行器設計和體系結構設計實際上存在相互耦合關系。解決飛行器設計的系統工程過程嵌套于解決體系結構設計的體系工程過程中，這種嵌套關系實際上決定了飛行器體系優化設計問題應該是一個飛行器設計與體系結構設計相互迭代的緊耦合問題。

飛行器為作戰體系的重要組成部分，但其設計過程通常獨立于體系結構設計之外。以自身性能最優為目的的傳統飛行器設計是無法保證其參與體系效能最優的[22]。因此，必須采用緊耦合方式，開展面向體系效能最優的飛行器/體系結構耦合優化設計。

將飛行器體系優化設計定義如下：面向體系運行任務環境，利用優化方法，在滿足各類約束的條件下，通過飛行器與體系的耦合設計，最終實現體系效能的最大化。

相比于傳統的飛行器設計，飛行器體系優化設計有如下特點：

1) 飛行器體系優化設計以體系運行需求為中心開展[21]。這增加了設計分析與需求之間的直接聯系，一方面依據需求評估體系效能，另一方面效能評估的結果用于驗證與改善需求。

2) 以往基于人工迭代的方式通常追求一個可行解即可，而飛行器體系優化設計強調通過優化手段實現設計協調過程自動化，使最終設計方案盡可能是全局最優解，進一步改善設計結果。

3) 體系設計與飛行器設計相互嵌套，包含由于原先二者相互獨立優化所忽略的耦合，實現了它們的耦合優化設計。

4) 優化設計追求的目標不再是單一飛行器性能最優，而是通過組成系統相互協調達到體系效能最優，即實現整體大于部分之和。

5) 表現出相較于傳統飛行器設計更為復雜、明顯的多學科耦合特性，不僅體現在飛行器內部各分系統之間，還體現在成員系統之間，它們彼此組網通訊、協同工作，才能完成體系任務。

6) 設計對象不再僅是飛行器自身，還需要與需求方協調飛行器性能指標與應用方案，飛行器設計者的角色從性能指標實現者轉變為提供者，產生的性能指標能夠指導飛行器創新設計。

7) 主要定義在體系與飛行器概念設計階段，通過兩概念設計過程的循環迭代，產生較優的概念設計方案作為初步設計的輸入。文獻[5, 21]就是著重考慮在體系背景下的飛行器概念設計問題。

因此，飛行器體系優化設計相比于傳統的飛行器設計和體系結構優化設計在建模和求解等環節都存在較大區別。在第2節和第3節中將給出詳細的建模方法和求解流程。

2 飛行器體系優化設計模型

2.1 優化模型

根據體系工程原理，飛行器體系優化設計問題的數學模型可以定義為飛行器優化設計問題(式(1))和體系優化設計問題(式(2))的結合，即

(3)

式中：各層級的設計變量xsos、xsys和xsubsys共同構成了優化問題的設計變量；x，ysos、ysys和ysubsys為各層級系統的狀態變量，由函數F(包含Fsos、Fsys和Fsubsys)計算，優化問題的不等式約束g(由gsos、gsys和gsubsys組成)、等式約束h(由hsos、hsys和hsubsys組成)和計算目標函數OBJsos均屬于特殊的函數F。從數學定義上看，該優化問題中各層級設計變量緊密耦合，體現了耦合設計的本質，其作為整體由單獨優化器統一處理。

2.2 體系架構

體系具有明顯的層次性，其中的成員是由比它低一層次的成員及其交互關系構成，而這個成員本身又是比它高一層次成員的組成要素[26]。因此，體系是在具有“樹”型結構的層次型系統的基礎上增加了同層子系統之間的耦合關系(不包含隸屬于不同系統的子系統之間的耦合)而構成。根據飛行器類對象特點，飛行器體系可分解為包含體系、系統和子系統的3層級架構，如圖1所示。

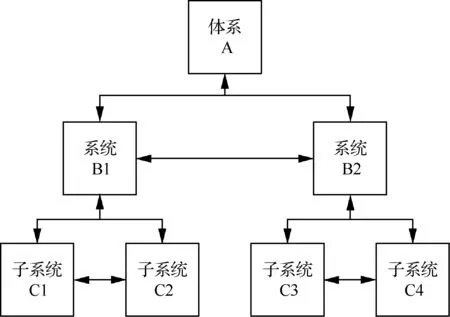
圖1 體系架構Fig.1 SOS architecture

對于體系架構建模來說，主要根據體系能力需求確定體系組成，并梳理成員的輸入輸出變量及其之間的交互關系，從而為學科建模與優化求解作準備。其中成員間的交互關系通過耦合變量的形式體現，包括同層級耦合變量和跨層級耦合變量。各成員包含的設計變量、常量、狀態變量和成員間的耦合變量共同構成該成員的輸入輸出變量。按照成員所屬體系層級的不同，其輸入輸出的組成也有所不同。對體系層、系統層和子系統層3級成員的輸入輸出分別定義如下：

1) 體系層

位于體系層的成員代表最頂層成員，沒有來自上層成員的輸入，輸出的狀態變量除包含其特有的體系優化目標外，還包含所有成員均具有的用于約束條件的狀態變量gsos、hsos和用于觀察迭代進程的觀測狀態變量ysos。從該層成員輸入的xsos狀態變量ysos傳遞給下層成員，同時接受來自下層成員的設計反饋xsys、ysys。由于最頂層成員通常只有一個，所以沒有同層級的耦合變量。因此，最頂層成員的輸入輸出變量如圖2所示。

2) 系統層

系統層的成員代表中間層成員，同時有上層成員和下層成員的輸入輸出變量。由于中間層成員和最底層成員不止有一個，所以它們的輸入輸

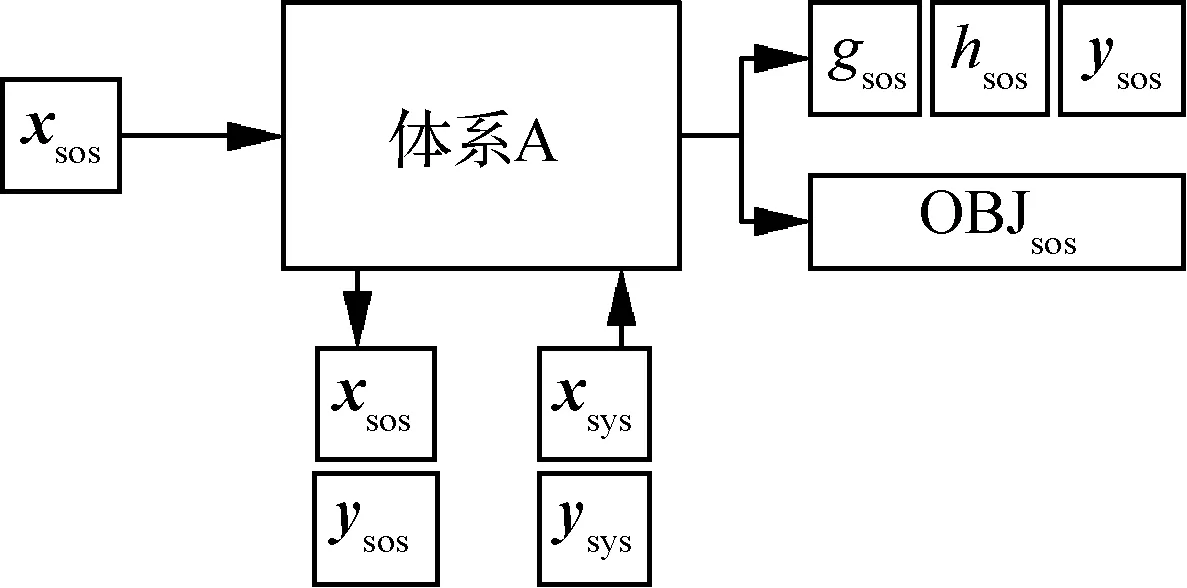
圖2 體系層成員的輸入輸出變量Fig.2 Input and output variables of SOS level members

出中還包含同層級的耦合關系，中間層的輸入輸出變量如圖3所示。

3) 子系統層

子系統層成員代表最底層的成員，最底層成員與中間層成員區別在于其沒有下層成員的輸入輸出，其輸入輸出變量如圖4所示。

在上述各層定義中，對輸入輸出變量的梳理實質上是將優化問題式(3)中緊耦合的設計變量x、耦合變量y、約束g和h按照所屬成員劃分為*sos、*sys、*subsys(*代表4個具體變量之一)，是抽象問題的具體化，為學科建模提供明晰的輸入。

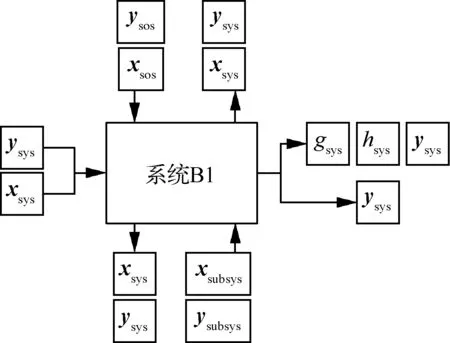
圖3 系統層成員的輸入輸出變量 Fig.3 Input and output variables of system levelmembers

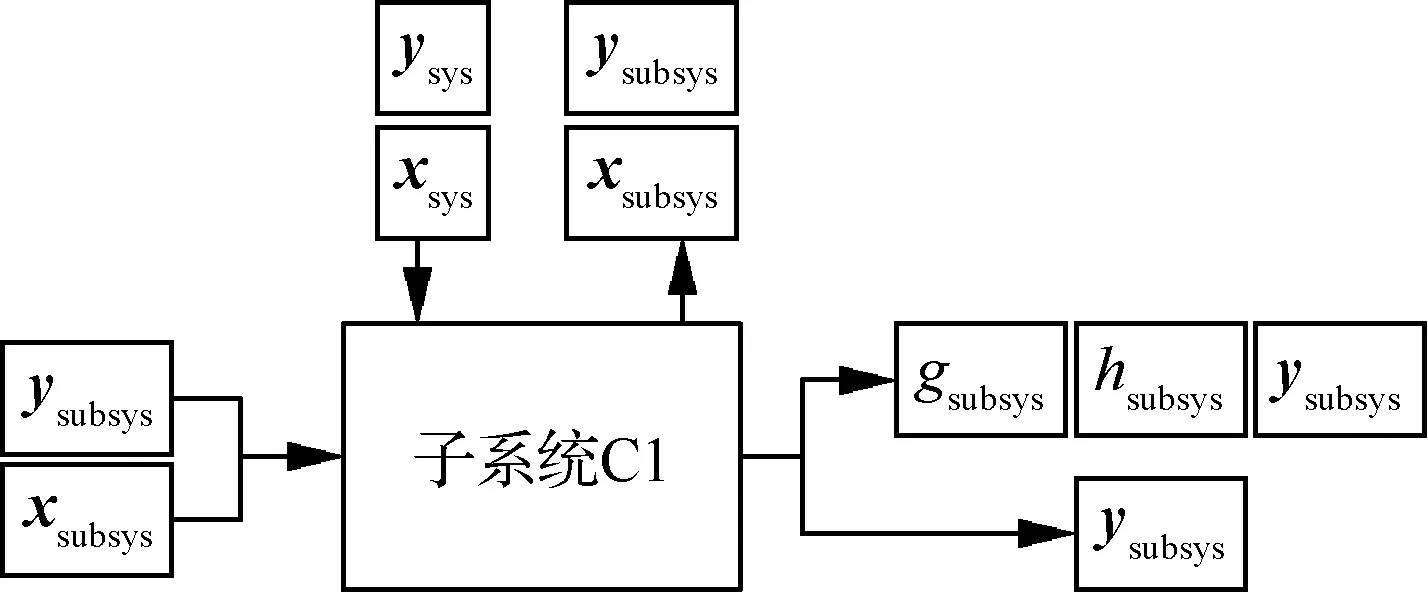
圖4 子系統層成員的輸入輸出變量Fig.4 Input and output variables of subsystem level members

3 飛行器體系優化設計求解

3.1 求解流程

飛行器體系優化設計問題的求解流程可分為問題定義、體系架構建模、學科建模、優化求解4個步驟，如圖5所示。各步驟的工作如下所述。

1) 問題定義：依據體系設計需求，構建與優化問題相關的體系運行環境，并確定式(3)表示的優化問題三要素(目標OBJsos、約束g和h、設計變量x)，即定性地對優化問題進行描述。

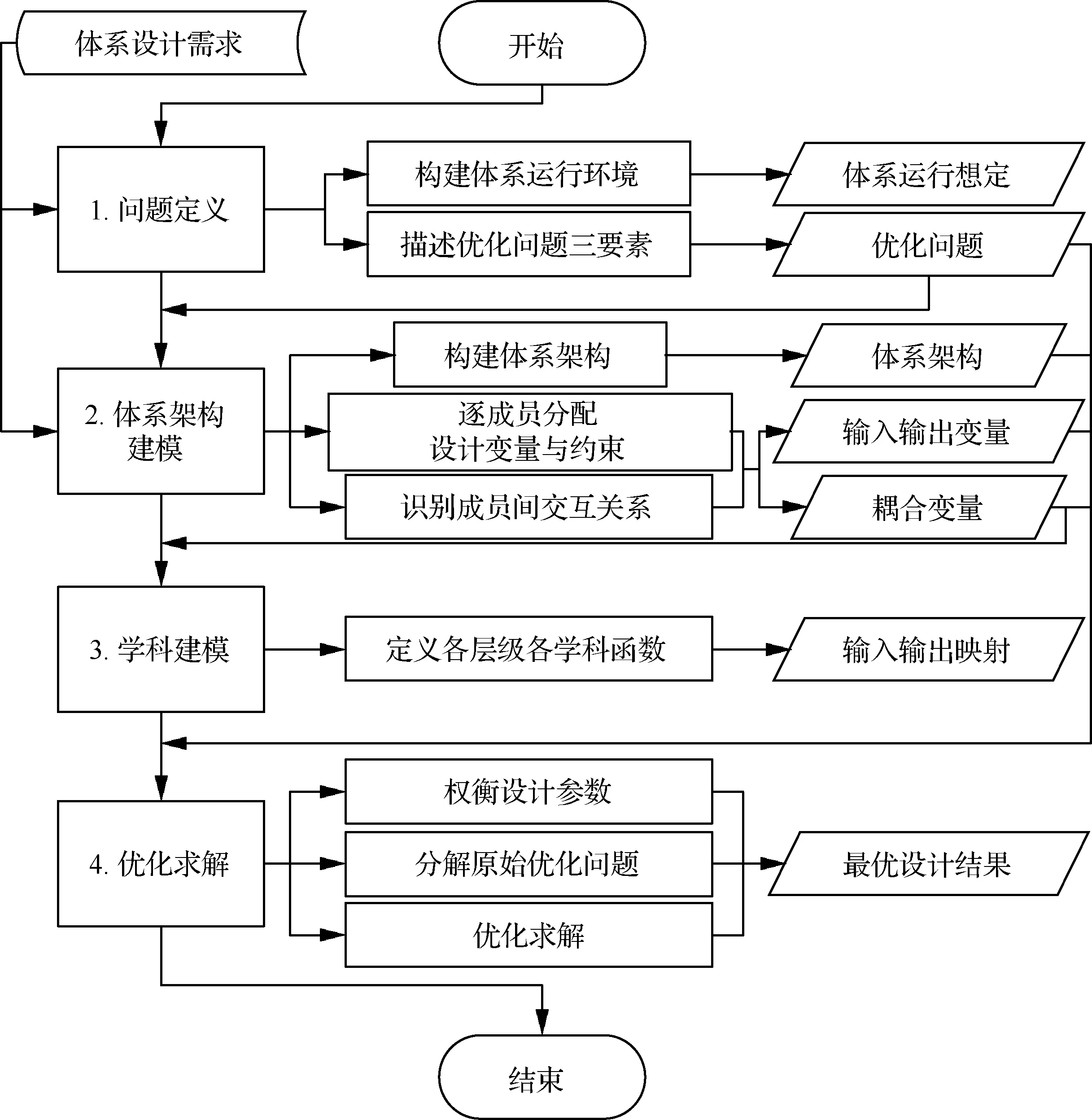
圖5 飛行器體系優化設計建模求解流程Fig.5 Modeling and solving process for flight vehicle SOS optimization design

2) 體系架構建模：依據第2節中體系架構建模的相關內容形成如圖1所示的體系架構，進而確定每個組成成員的輸入輸出變量及其之間的交互關系，為學科建模和求解提供輸入。

3) 學科建模：建立優化求解的模型體系，各成員對應的學科模型作為黑箱函數參與優化問題求解過程。一般來說，一個成員有且只有一個與之對應的學科模型，如發動機對應推進學科模型，但其可以包含多個函數F。反映體系問題設計目標的OBJsos屬于特殊的Fsos。飛行器作為體系中的系統級成員，函數Fsys的定義是飛行器設計過程的體現。

3.2 求解方法

多學科設計優化(MDO)技術作為一種有效求解復雜系統工程問題的手段，在飛行器等包含復雜耦合特征的系統優化中得到了大量成功應用[17, 19, 27]。飛行器體系是一個典型包含復雜耦合關系的層次系統，對其進行非層次化處理后，可以采用MDO技術來優化求解。這里采用拓展設計結構矩陣(XDSM)[28]來表示上述非層次MDO問題，如圖6所示。非層次化處理過程如下所述。

圖1中具有層級特性的體系成員與圖6中對角線上學科模型之間的對應過程即飛行器體系的非層次處理過程。圖1中成員數量與圖6中學科數量相同；各層級成員整體上按照體系層級由低到高、在XDSM中由左上角到右下角有序排列；當屬于同一系統的子系統排列完成后，緊接著排列此系統成員，如子系統成員C2右下角緊跟系統成員B1、系統成員B2右下角緊跟體系成員A。

這使得原先在體系架構中具有層級所屬關系的學科模型，當運用MDO求解時是等效的，對于上述非層次體系優化設計問題，可以采用任意MDO求解策略進行優化求解。

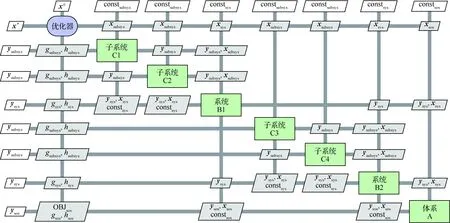
圖6 優化問題求解過程Fig.6 Solving process of optimization problem

4 巡飛/精打協同武器系統優化應用

本節以包括兩型導彈設計問題與作戰規劃問題的巡飛/精打協同武器系統作戰體系為例，構建其體系設計優化問題并對其進行求解，并將其和先飛行器設計后體系設計的串行解耦設計作對比分析。

4.1 巡飛/精打協同武器系統

巡飛/精打協同武器系統作戰以導彈編隊協同作戰為背景，包含巡飛打擊導彈(Loitering Attack Missile, LAM)和精確打擊導彈(Precision Attack Missile, PAM)兩型導彈，執行“偵查-打擊”一體化作戰任務。其中LAM執行偵查任務，為PAM提供戰場態勢信息，PAM在LAM的指引下完成對目標的打擊任務。

在體系指標不變情況下，僅從單個導彈系統最優的角度來設計系統時，PAM可以表示為滿足射程要求下質量最小，而LAM則可表示為滿足航程要求下質量最小，各導彈系統滿足最優設計后再到體系下評估其作戰效能。實際上導彈質量最小并不意味著體系作戰效能最佳，LAM巡航速度以及PAM的打擊精度等對作戰效能產生很大影響，但上述指標在單個導彈系統設計時更多是作為約束考慮。因此，需要同時進行體系設計和導彈設計，協調最佳的指標參數，以最大化體系效能。

4.2 問題定義

1) 體系作戰

以某一典型的巡飛/精打協同武器系統作戰場景開展研究，如圖7所示,圖中:2at與2bt為坦克目標在地面上近似為長方形投影的長和寬。由于體系下的指標體系較為復雜，其中作戰成本和任務時間是較為重要的評價指標，對整個作戰效能影響較大，且兩者互為約束，更能夠體現體系下的權衡特性，因此選擇其作為體系效能指標，即

min OBJsos=ωCCtotal+ωtttotal

(4)

式中：ωC和ωt分別為作戰成本Ctotal和任務時間ttotal的權重系數。

作戰流程分為2個階段。第1階段LAM對給定區域進行搜索，確定目標位置；第2階段PAM根據LAM提供的目標信息進行打擊，與此同時LAM在空中保持飛行，等待PAM攻擊目標后進行毀傷評估。體系作戰層約束包括：LAM設計飛行時間tLAM需大于作戰任務時間ttotal；為保證PAM順利打擊目標，其設計射程Rd需大于目標距離Rm；為保證LAM順利完成目標區域搜索，其設計搜索面積Asd需大于目標所在區域面積Asm。

2) LAM導彈系統

LAM在給定設計搜索面積Asd與設計搜索速度Vsd的條件下完成導彈設計，設計變量為導彈直徑dLAM和微型渦噴發動機的工作時間td。設計過程中要滿足LAM最大搜索面積Asp大于給定設計搜索面積Asd；還應限制長度lLAM以滿足裝載要求。

3) PAM導彈系統

PAM在給定設計射程Rd的條件下完成導彈設計，其設計變量包含PAM直徑dPAM和單室雙推固體火箭發動機的兩級推力F1、F2和工作時間t1、t2。設計過程中，PAM實際最大射程Rmax要大于給定的設計射程Rd；PAM長度lPAM也需要滿足同樣的裝載條件。對于發動機來說，其兩級推力比和裝藥燃速BR均有一定限制。另外，PAM需滿足飛行條件限制，需要約束一級發動機結束末速度V1、落點速度Vend和最大飛行速度Vmax。

4) 協同作戰

為完成打擊任務，目標毀傷概率Wco應高于最低毀傷概率需求Wre。

根據以上描述，巡飛/精打協同武器系統優化問題的數學定義為

(5)

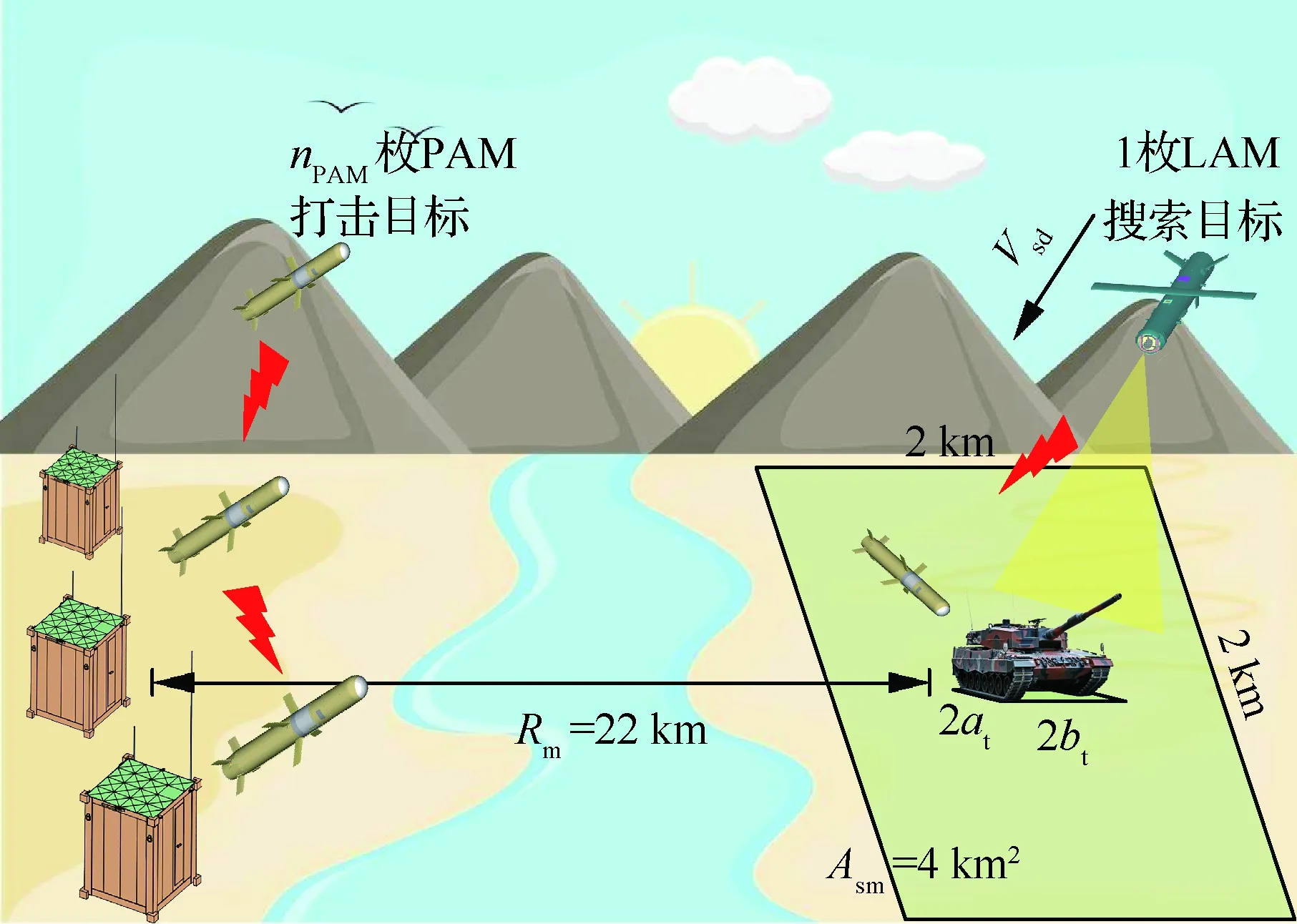
圖7 巡飛/精打協同武器系統作戰應用案例Fig.7 Combat case of LAM/PAM cooperative weapon system

式中：nPAM為PAM的數量。

4.3 體系架構建模

根據4.1節中對體系優化問題的描述，以及巡飛/精打協同武器系統具備的功能，體系架構如圖8所示。整個體系結構包含3層：第1層為體系層，指巡飛/精打協同武器系統作戰體系；第2層為系統層，包含LAM導彈、PAM導彈以及協同作戰單元；第3層為子系統層，每個導彈系統都包含推進系統、結構質量、氣動外形和制導控制4個模塊，而協同作戰包含PAM射擊效率評估和任務規劃模塊。

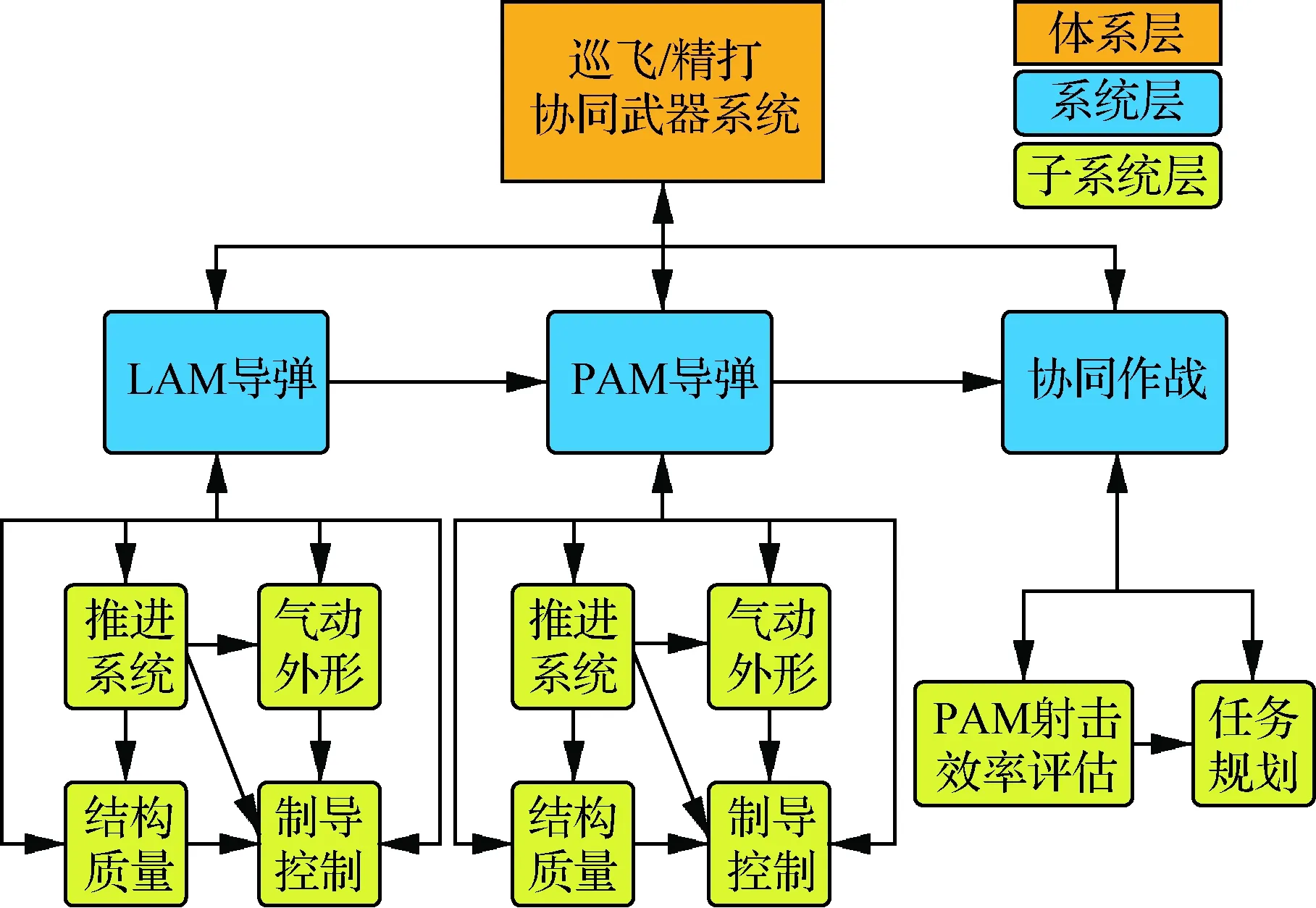
圖8 巡飛/精打協同武器系統作戰體系架構Fig.8 SOS architecture of LAM/PAM cooperative weapon system

4.4 學科建模

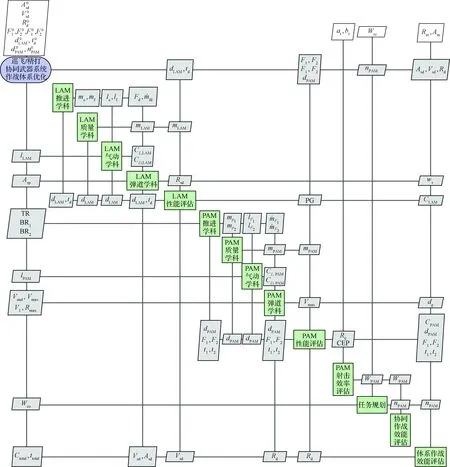
Note: CEP—Circular Error Probable圖9 巡飛/精打協同武器系統優化問題求解流程Fig.9 Solving process of optimization of LAM/PAM cooperative weapon system

4.5 求解方法

1)飛行器體系優化

對上述巡飛/精打協同武器系統作非層次化處理。采用多學科可行(MDF)求解策略，采用NSGA-II多目標遺傳算法作為頂層優化求解器。種群大小選擇為80，進化代數選擇為200代。

優化后的得到的總任務時間ttotal與總任務成本之間Ctotal的Pareto前沿如圖10所示。從圖10中可以看出優化問題兩目標之間的矛盾關系，即若追求任務成本最小，那么任務完成時間就較長，當導彈編隊打擊時敏目標時，則可能由于打擊時間過長，目標有充足時間進行規避，導致打擊失敗；若追求任務總時間最小，雖能夠盡可能保證有效打擊時敏目標，但帶來的負面影響是任務總成本的提高，當目標重要性不高時，會導致任務費效比有所提高。

處在Pareto前沿上的最優解所代表的導彈設計方案存在一定差異，在這里選擇了任務時間最小、任務成本最小和兩目標歸一化加權和最小3組具有代表性的導彈設計結果列在表1中。可以看出，在整個Pareto前沿上權衡導彈設計方案時，PAM設計變量對體系效能的影響相比于LAM更為顯著。因此，在最終方案決策時，應重點考慮PAM的設計優化。

圖10中的菱形標記為采用平均加權和作為單目標函數時，采用自適應模擬退火(ASA)算法優化后的最優結果。可以看出，和Pareto前沿上多目標優化平均加權和最小的結果相比，單目標優化結果仍落于Pareto前沿上，但并沒有完全重合，這說明兩類算法的收斂趨勢是基本一致的，但由于體系優化問題的復雜性，收斂到實際最優解具有一定難度。

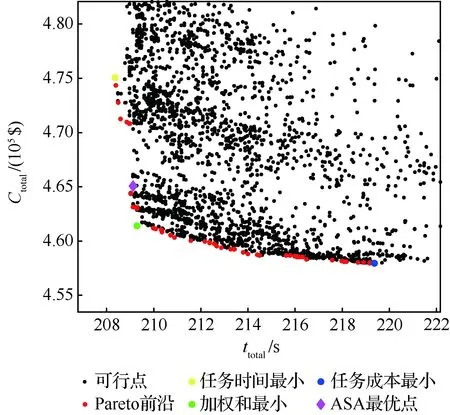
圖10 ttotal與Ctotal構成的Pareto前沿Fig.10 Pareto front of ttotal and Ctotal

2) 與傳統設計模式對比

為便于對比，在這里同樣給出按照傳統設計模式，即先對導彈進行設計再將其運用于體系作戰的思路獲得的設計結果。由于傳統設計模式串行進行，導彈設計的輸入為體系作戰想定的任務參數，即LAM為完成給定區域Asm搜索任務，按照質量最小準則設計，PAM為完成打擊距離為Rm目標的任務，同樣按照質量最小的準則設計；兩型導彈設計完成后用于體系作戰中驗證設計結果。其優化設計結果如表1所示，通過與飛行器體系優化設計結果(取兩目標歸一化加權和最小的一組結果)的對比可以看出，飛行器體系優化設計模式能夠有效地縮短任務時間、降低任務總成本，圖11和圖12更為直觀地表示了兩設計模式所得兩型導彈優化結果對比。

可以看出，耦合設計和“先設計后使用”的設計模式產生了截然不同的設計結果。“先設計后使用”的設計模式雖然能夠滿足導彈自身的設計約束，但當其用于體系作戰時，由于LAM飛行時間的限制，雖能夠完成對作戰區域的搜索，但是無法再為PAM攻擊提供指引，即沒有滿足LAM設計飛行時間tLAM需大于作戰任務時間ttotal的約束；另外，需要多達21枚PAM才能滿足毀傷概率需求，這是因為PAM和LAM僅獨立滿足自身的約束，沒有考慮共同體系作戰時的性能匹配性。

一方面是由于“先設計后使用”的思路沒有考慮體系作戰環境，即使能實現導彈自身的最優設計，但當其在作戰中實際使用時，可能會出現體系效能不佳或根本無法完成體系任務的問題；另一方面是由于按照傳統設計思路設計導彈時，沒有考慮導彈設計對體系效能的貢獻，也就是說導彈設計與體系規劃的獨立考慮引入了附加的設計目標，忽略了導彈設計參數對體系效能的直接影響，這是現階段設計模式普遍存在的問題。

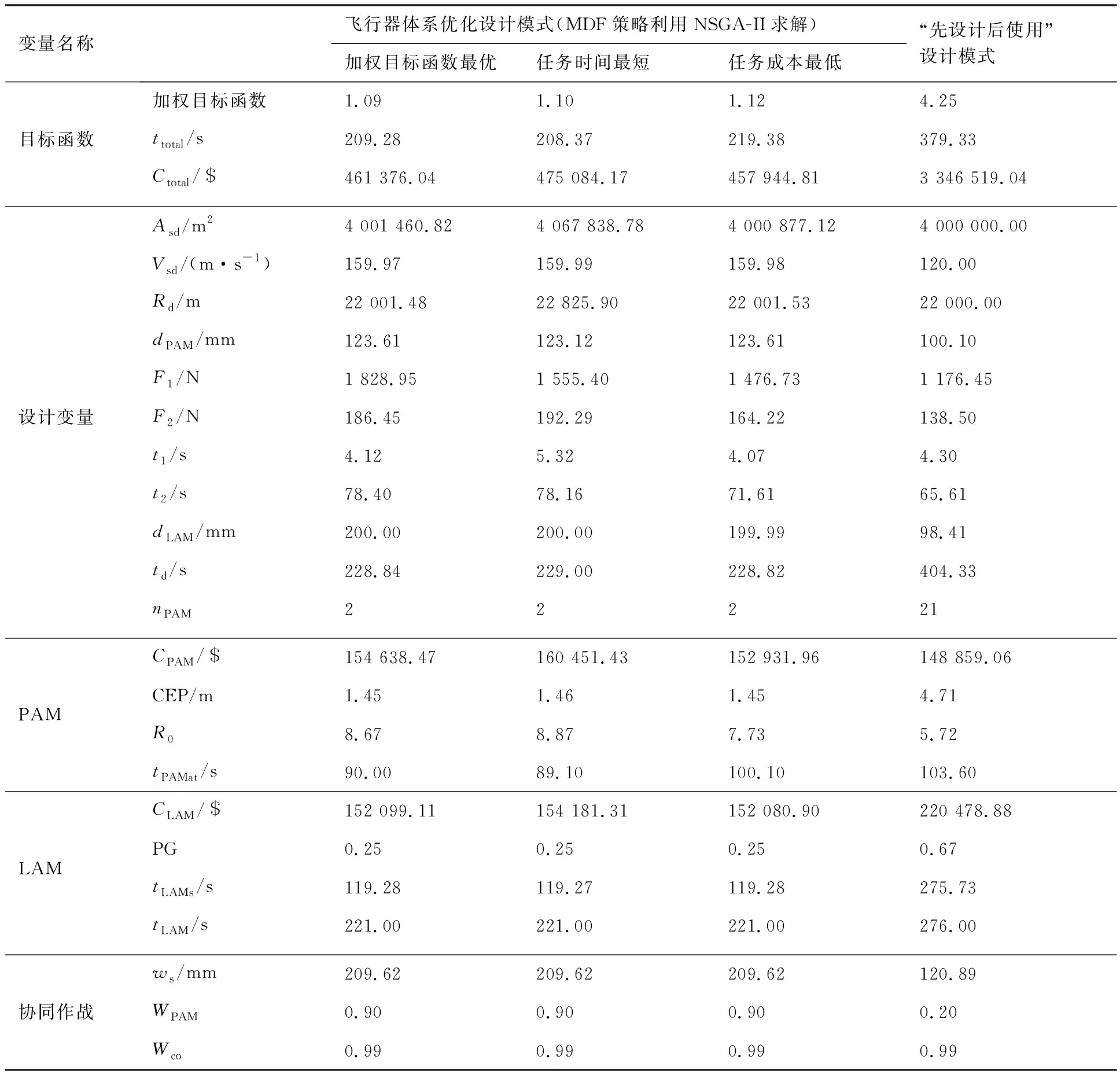
表1 巡飛/精打協同武器系統優化問題優化結果Table 1 Optimization results of LAM/PAM cooperative weapon system

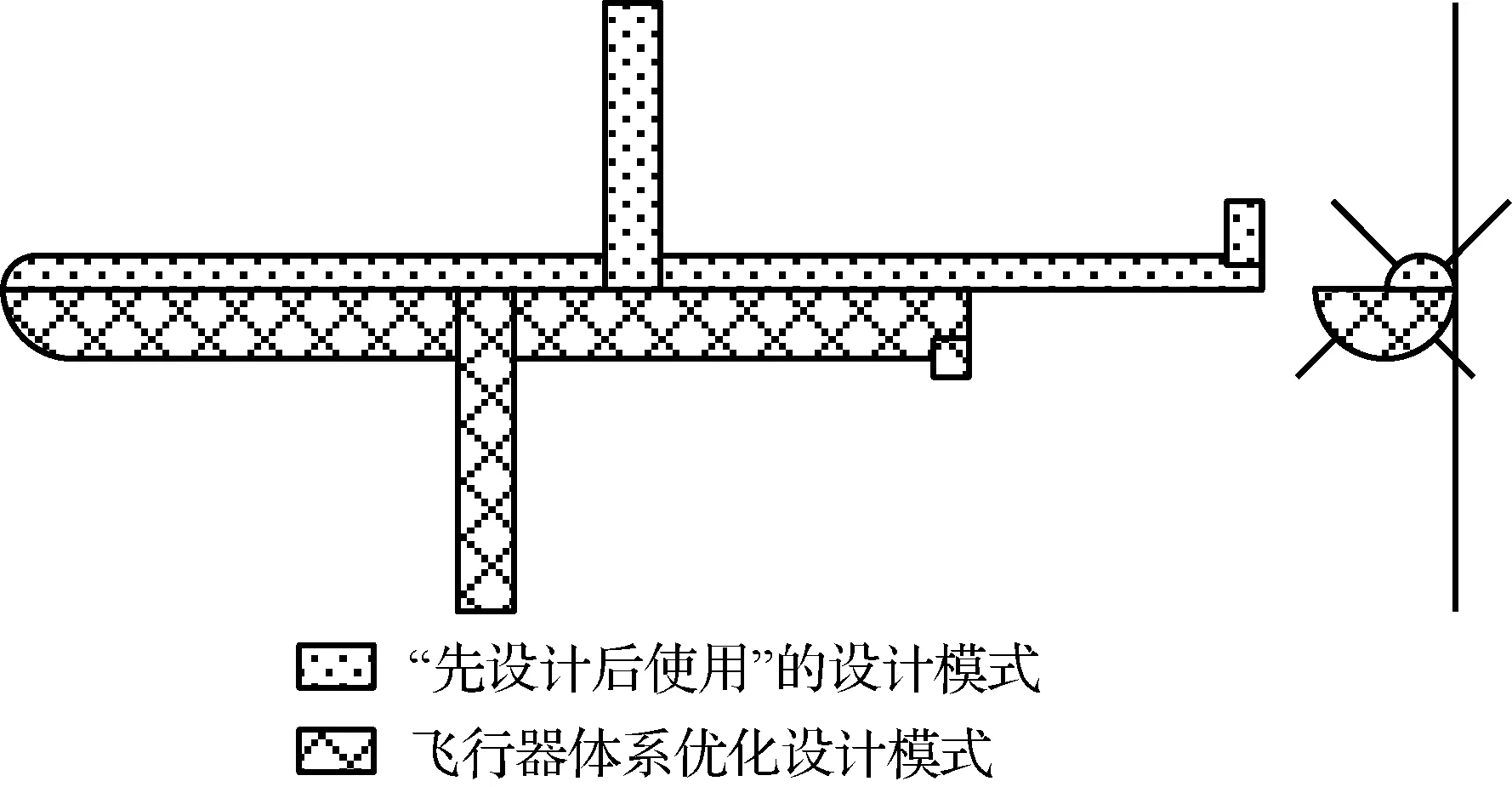
圖11 兩種設計模式對應的LAM設計結果Fig.11 LAM design results corresponding to two types of design modes

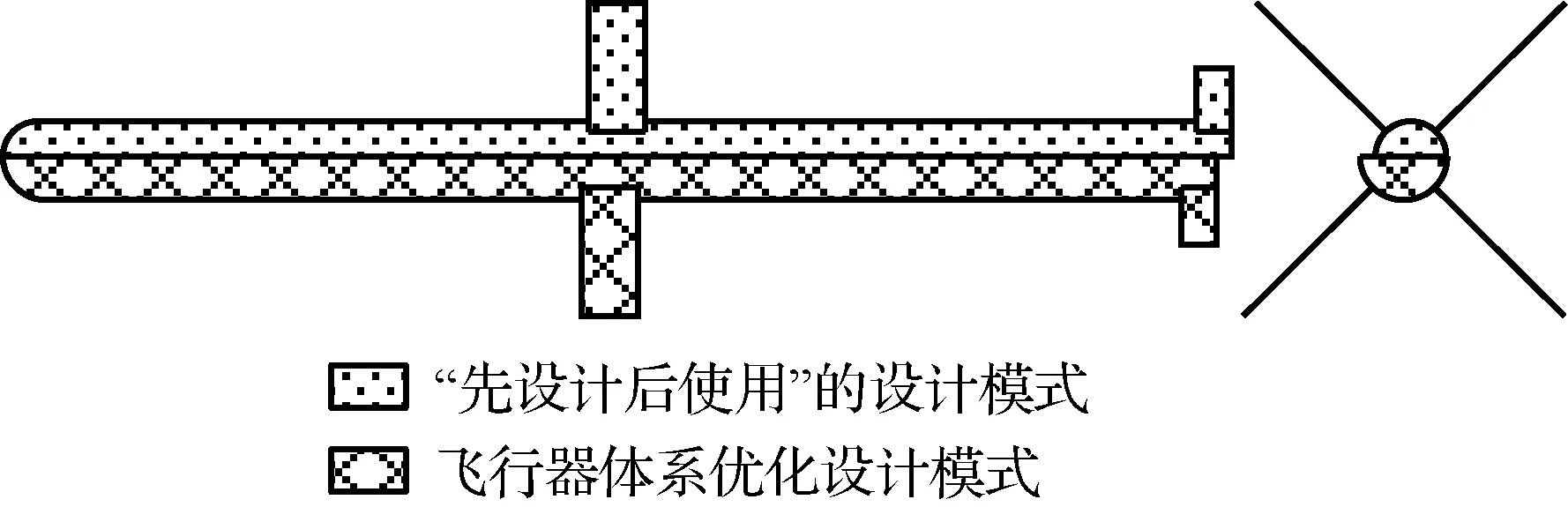
圖12 兩種設計模式對應的PAM設計結果Fig.12 PAM design results corresponding to two types of design modes

5 結 論

以巡飛/精打協同武器系統作戰為例，發展了一套面向飛行器性能和體系結構耦合設計的飛行器體系優化設計的建模與求解流程，研究表明：

1) 設計飛行器時，有必要將傳統飛行器設計模式轉變為飛行器體系優化設計模式，使設計的飛行器能夠更好地完成體系任務，體系作戰效能得到進一步提升。

2) 本文提出的方法雖以飛行器及其構成體系的設計為重點，但是此方法仍可應用于其他體系及組成系統耦合設計領域。同時，通用的優化設計問題以及通用的建模求解流程為其應用研究與關鍵技術研究提供了必要的理論基礎。

由于本文中所采用的算例的目的是驗證所提方法的可行性，因此，相較于更具有一般意義的體系設計問題來說考慮得較為簡單。在實際應用于更復雜的體系設計問題時，為了捕捉體系的涌現性，需要借助如建模與仿真的手段來評估體系效能；同時，由遺傳算法和模擬退火優化結果存在一定差異性可以看出，飛行器體系優化問題相比于普通MDO問題其復雜性更高，需進一步研究更為魯棒高效的優化算法和求解架構，以提升求解能力；另外，隨著優化問題復雜度的提升，必須要考慮體系中普遍存在的不確定性影響，還需要研究基于不確定性MDO體系問題的建模和優化求解。