基于蟻群算法的煙氣中人員疏散路徑選擇優化*

江奎東, 毛占利, 陳浩楠, 歐陽爾耀

(中國人民武裝警察部隊學院 消防工程系，河北 廊坊 065000)

0 引言

伴隨經濟的飛速發展，火災對社會的負面影響愈發凸顯，安全疏散已成為保障人員生命安全的重要手段之一。除人群的內部因素之外，火災產生的熱煙氣以及火源自身的熱輻射等外部因素，也極大地影響著疏散效率。

Predtechenshi等[1]通過分析實驗數據，得到疏散狀態對人員疏散速度的修正參數；Roytman[2]給出擁擠程度及其他影響因素對疏散過程產生的綜合效應；Bryan等[3]改進傳統啟發式選擇出口，將貝葉斯等理論納入疏散決策模型中，盡可能高保真還原疏散時的決策傾向與特征；Fruin等[4]通過研究有限空間下疏散人群的特征，得到疏散流量、人員密度、疏散寬度以及疏散速度之間的關系式；Elvezia[5]研究人流過飽和狀態對疏散的影響，提出“疏散容量”概念，得到報警時間、路徑長度、出口寬度及控制瓶頸上游流量對疏散容量的影響；Enrico等[6]研究煙氣對人群疏散行為的影響，通過研究隧道疏散中的非刺激性煙氣，得到不同消光系數下的人員行走速度；王帥等[7]通過疏散實驗的方法，得到視線受影響下疏散通道寬度對疏散能力的影響；陳慶全等[8]將環境網格化融入蟻群算法，得到給定環境條件下的最短疏散路徑的選擇算法。

總結現有研究可知，疏散的模擬還原方法包括節點博弈選擇求解最短路徑以及最短歐式距離的統計計算。為了模擬疏散環境、人員心理等因素對疏散的影響，可在以上模型中耦合1個或少量的修正函數，但當前研究中，修正函數對于疏散過程影響的研究相對靜態，多以某1影響參數對特定時刻下的疏散速度進行修正，沒有很好地結合整個動態疏散過程，致使疏散人員過度收斂于某1條路徑中，產生瓶頸效應。基于此，本文將火災中的能見度和人員密度，與蟻群算法進行耦合，考慮火災的實際情況，以最短疏散時間為目標函數，提出1種最優疏散路徑的算法模型。

1 模型介紹

1.1 模型構建

1.1.1 模型合理性分析

當前疏散模型研究主要可以分為2大方向：一是外界及人員心理對疏散的修正，主要研究修正因素與疏散速度、時間的函數關系，如人流密度對疏散速度的影響，行人對不同人流路線趨向性選擇[9-11]等，缺點是這類模型不能夠直接求出路徑解；二是基于算法的全局搜索模型，求解靜態空間內最短疏散路線，如元胞自動機搜索疏散最短路徑[12]等，但由于受模型自身限制，模型很難較好地融合多個修正參數。由此可見，目前研究中還缺少1種能實時反饋環境及人員變化的動態多參數模型。蟻群算法則是1種具有很強并行性與反饋性的算法，因此，本文將能見度和人員密度與蟻群算法進行耦合。

1.1.2 人員密度模型

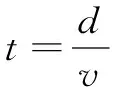
vρ=v0(εA+θB+γ)

(1)

A=1.32-0.82ln(ρ)

(2)

B=3.0-0.76ρ

(3)

式中：權重系數ε∈[0.25,0.44]，θ∈[0.014,0.088]，γ∈[0.15,0.26]，由此可以計算特定人流下的疏散速度。

由Predtechenshi與Milinskii[1]的研究得到不同疏散形式對疏散速度的修正公式。對于垂直疏散，如式(4)所示：

v=μ×vρ

(4)

對于水平疏散，如式(5)所示：

μ=σ×d

(5)

式中：當疏散過程為垂直疏散時，μ=1.21；當疏散過程為水平疏散時，σ為水平修正系數，σ∈[0.36,1.49]；d為疏散通道或門的寬度。

1.1.3 能見度模型

煙氣對人員疏散的速度同樣產生影響。火災中的懸浮物，具有很強的消光性，直接導致環境能見度大大降低，致使疏散速度變慢，疏散時間延長。能見度可表示為：

(6)

式中：C是經驗常數；M是煙氣粒子的質量濃度；Km是煙氣粒子的消光率。根據《Fire Engineering》中的數據可知，火災中一般的木材和塑料的消光率Km=7.6 m2/g，熱解過程的發煙消光率Km=4.4 m2/g。

能見度確定后，采用式(7)計算出疏散速度：

(7)

將式(1)，式(4)和式(7)耦合，得到已知人員密度在煙氣影響下的修正疏散速度公式：

(8)

1.2 蟻群算法

由意大利學者Dorigo提出的蟻群算法[13-14]屬于仿生算法的一種，由于該算法具有良好的分布式計算、正反饋催化以及高度并行性的優點，非常適用于選擇及優化路徑問題[15-16]。螞蟻會趨于選擇信息素濃度較高的路徑，蟻群會在這一正反饋的機制下逐漸集中于這條路徑，該路徑即為最優解。

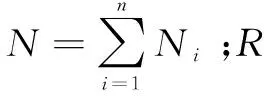
螞蟻k(k=1,2,…,m)在共計K=NCmax次的迭代過程中，除按照之前蟻群留下的信息素濃度進行概率選擇外，還要將已走過的節點更新進禁忌表tabuk(k=1,2,…,m)中。對于選擇概率，按照下式計算：

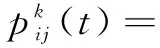
(9)

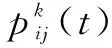
(10)

式中：dij為(i,j)路段的幾何長度，可看出，啟發函數中路段長度對螞蟻選擇的概率大小起到重要作用。

1.3 啟發函數的優化耦合

傳統蟻群算法的啟發函數，多采用距離的倒數[11]。但對于人員疏散問題，路徑間優劣的判斷往往是比較路徑間的疏散時間。因此本文算法改變傳統的啟發規則，使得環境等多個因素對行人影響得以綜合地在疏散路徑的選擇過程得以體現。在1.1中，已經給出在火災煙氣狀況下的疏散速度計算公式。而在給定的環境網格中，網格的長度dij是固定值，計算時不影響螞蟻的選擇。在此，將修正速度v代替路徑長度倒數，得到新的啟發函數：

(11)

為了加速算法收斂，同時保證螞蟻在搜索階段具有較好的遍歷性與隨機性，算法引入蒸發系數φ，使得路徑中殘留信息素會隨著時間而蒸發掉。(i,j)路徑中信息素按照式(12)更新：

(12)

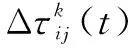
(13)

式中：Q為常量；Lk為螞蟻k在本次搜索中走過的總路程長度。在該模型下，路徑越短，信息素增量越大，同時能更快檢索到最優路徑，算法流程如圖1所示。

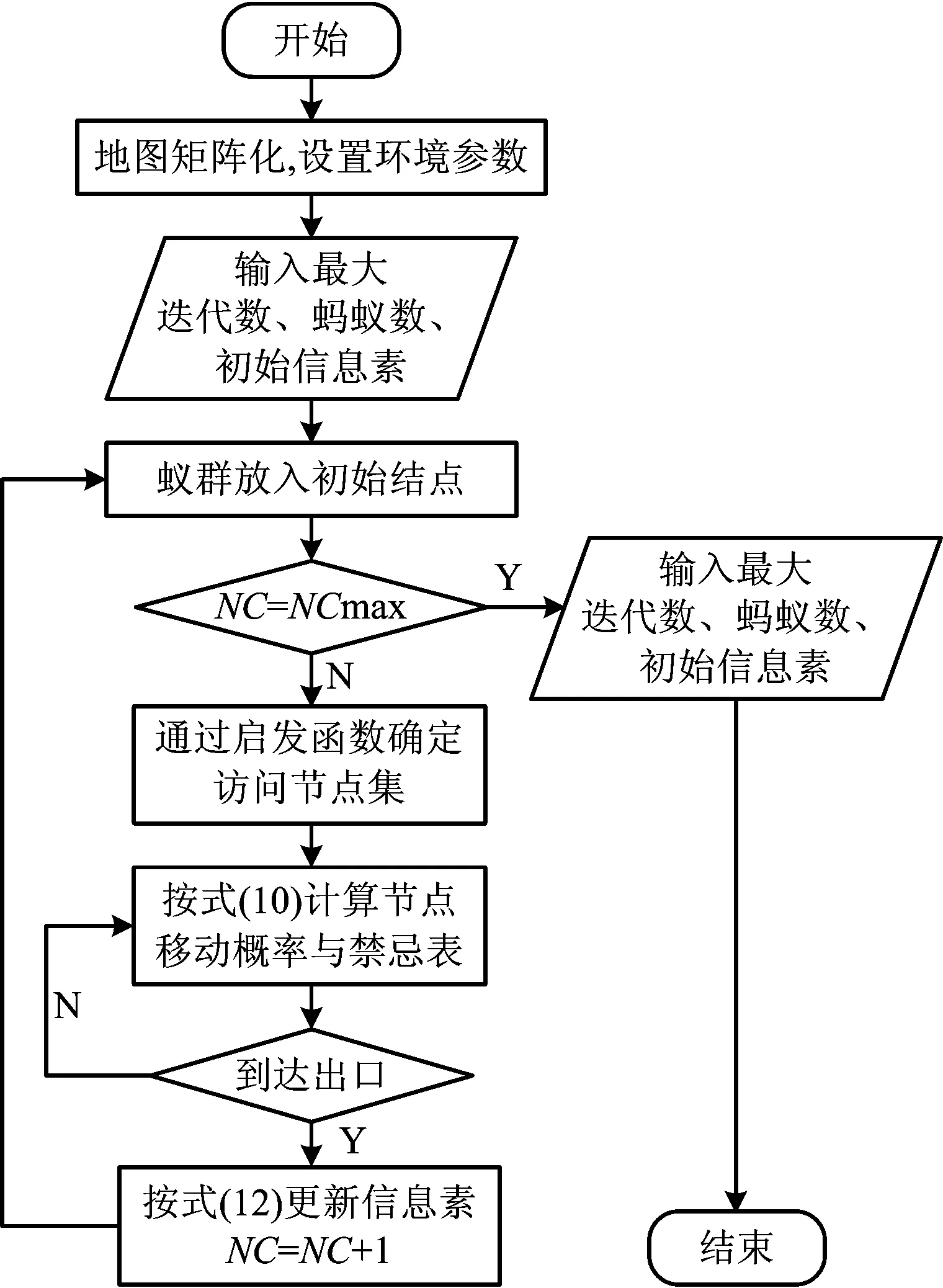
圖1 算法流程Fig.1 Algorithm flowchart

2 工況檢驗

2.1 參數設定及其收斂性

本文采用文獻[18]中構建的30×30柵格地圖，設定本次疏散的人群密度為2.3人/m2，最優路徑為疏散時間最短的路徑。

蟻群算法的各項參數決定了其算法的收斂性。不同環境下參數差距較大，目前這些參數采取數值模擬迭代計算獲得。經調試，本次運行參數的賦值如表1所示。

在該參數下，隨機取點檢測收斂性，見圖2，該組參數得到的收斂效果較好，本文均采用該工況的優化參數組。

表1 算法運算參數Table 1 Algorithm operation parameters

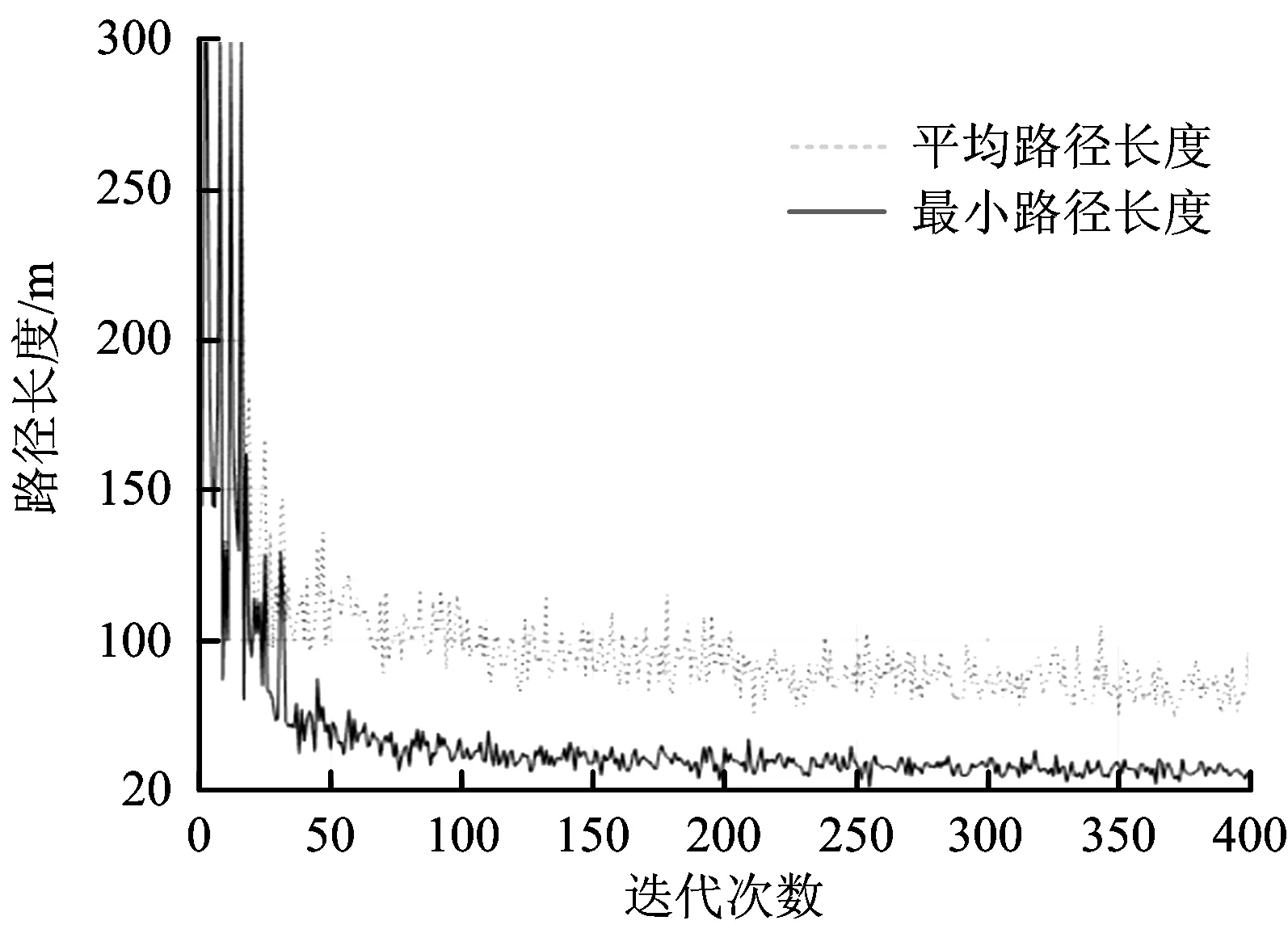
圖2 算法收斂性Fig.2 Algorithm convergence

2.2 疏散最優路徑求解

2.2.1 火災初期的路徑求解

在整個火災發展過程中，環境各項參數都會實時變化。隨著火焰和煙氣的蔓延，通行柵格能見度會發生改變，本次仿真過程選擇火災初期發展階段。通過Matlab繪制各代螞蟻遍歷路徑以及最優路徑。

圖3中，非灰色柵格為可通行區域，螞蟻根據網格中賦值的信息采用貪心算法選擇步行節點；灰色柵格為障礙區域，螞蟻不可通行。中央三角標記點為螞蟻初始位置，即疏散起點；邊緣圓形標記點為出口位置，即疏散終點；邊緣加粗且標記S的柵格群為火災煙氣影響區域，在非灰色柵格中，疏散能見度D=30。而在煙氣影響區域中，由于火災生成的固體顆粒與熱解煙氣產物，能見度受限，設定D=1，將各參數帶入優化蟻群算法，可得表2。

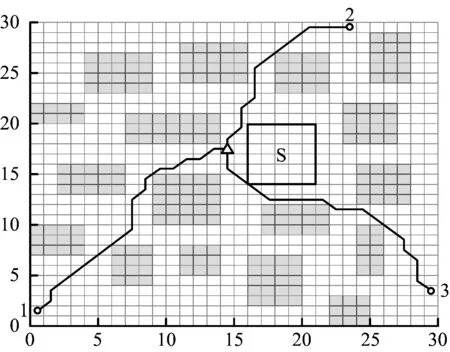
圖3 各出口的最優路徑Fig.3 Optimal route maps of each exit

表2 各路徑下的疏散結果Table 2 Evacuation results

綜上可知，最短疏散時間關系為T3>T1>T2，最短疏散距離關系為L3>L1>L2,可知在火災初期，最佳疏散出口為出口2。

2.2.2 火災中期的路徑求解

在實際火場中，煙氣會隨火災發展而蔓延，不同位置煙氣濃度也不盡相同，造成能見度不均勻，致使疏散速度發生變化，進而影響疏散路徑的選擇。在算法環境構建中，具體數值及視覺柵格圖分別如表3和圖4所示。

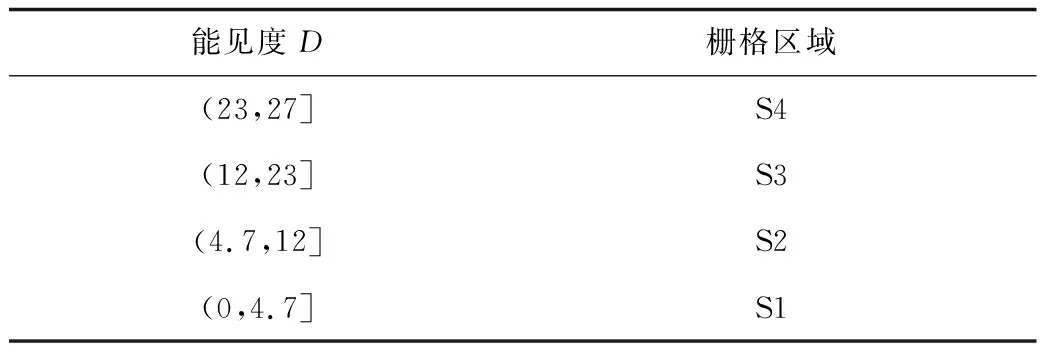
表3 能見度范圍Table 3 Visibility range

圖4中，柵格網絡圖中定義：邊緣圓形標記地圖的3個安全出口的位置，分別記為出口1，2，3；加粗柵格群為煙氣蔓延區域，人群在此通行時，疏散速度受能見度的修正。

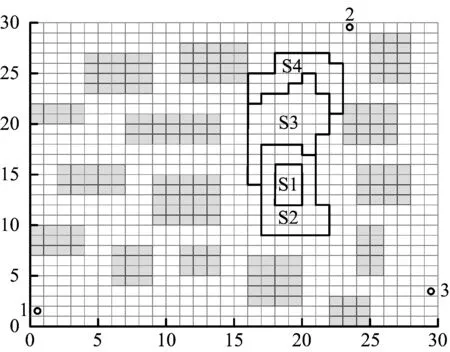
圖4 疏散環境柵格Fig.4 Evacuation raster graphic

采用優化蟻群算法，可得各出口的最優路徑圖、最優疏散距離及最短疏散時間，分別如圖5和表4所示。

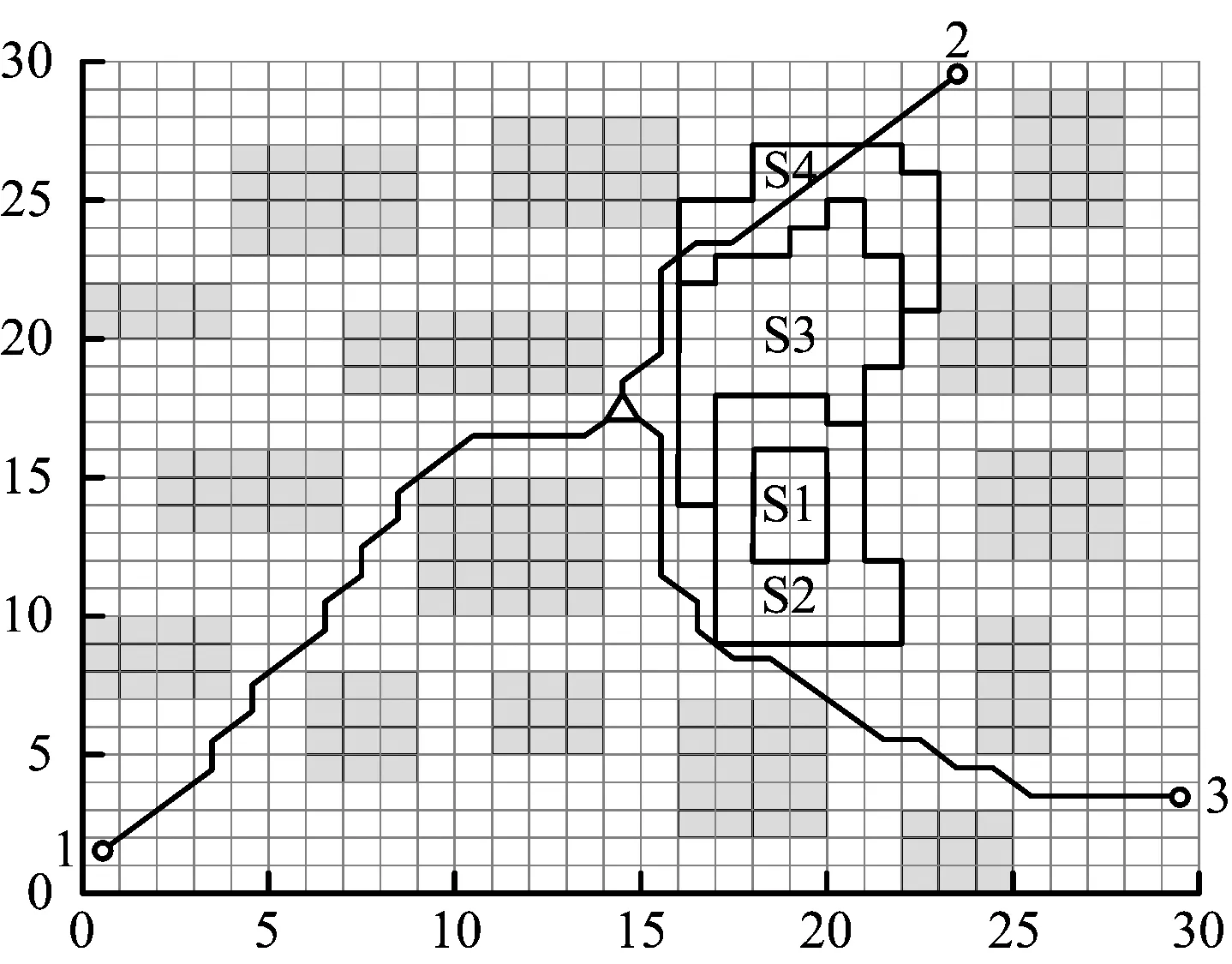
圖5 各出口的最優路徑Fig.5 Optimal route maps of each exit

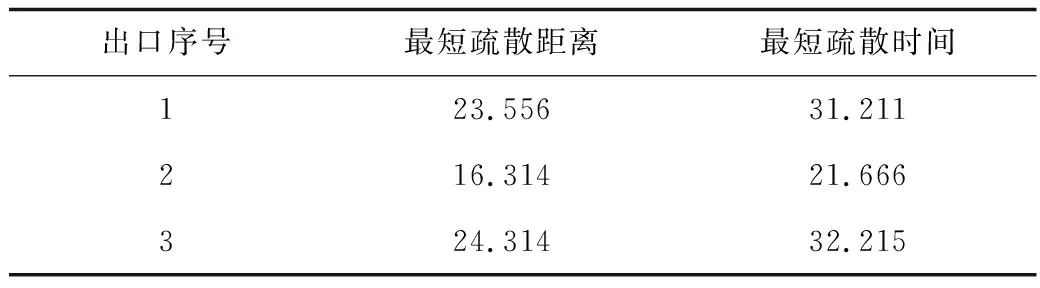
表4 各路徑下的疏散結果Table 4 Evacuation results

綜上，各出口最短疏散時間的大小關系為T3>T1>T2，最短疏散距離大小關系為L3>L1>L2，故優化蟻群算法求出最佳疏散出口為出口2，疏散時間為21.666，疏散距離為16.314。

2.3 結果對比

本文模型結果與文獻[18]中最優路徑進行對比，對比結果如圖6所示。

文獻[18]中最佳疏散出口為1號，見圖6(b)，疏散距離為23.556，本文模型規劃的新路徑長度16.314。因為在實際火災中，由于火災發展程度不同，所造成某一位置的煙氣濃度、溫度及熱輻射等參數不盡相同。當火災對該位置造成一定影響尚不足以阻滯通行時，這一位置節點依然可以作為疏散路徑，從而提高疏散路徑利用效率，減少疏散時間。

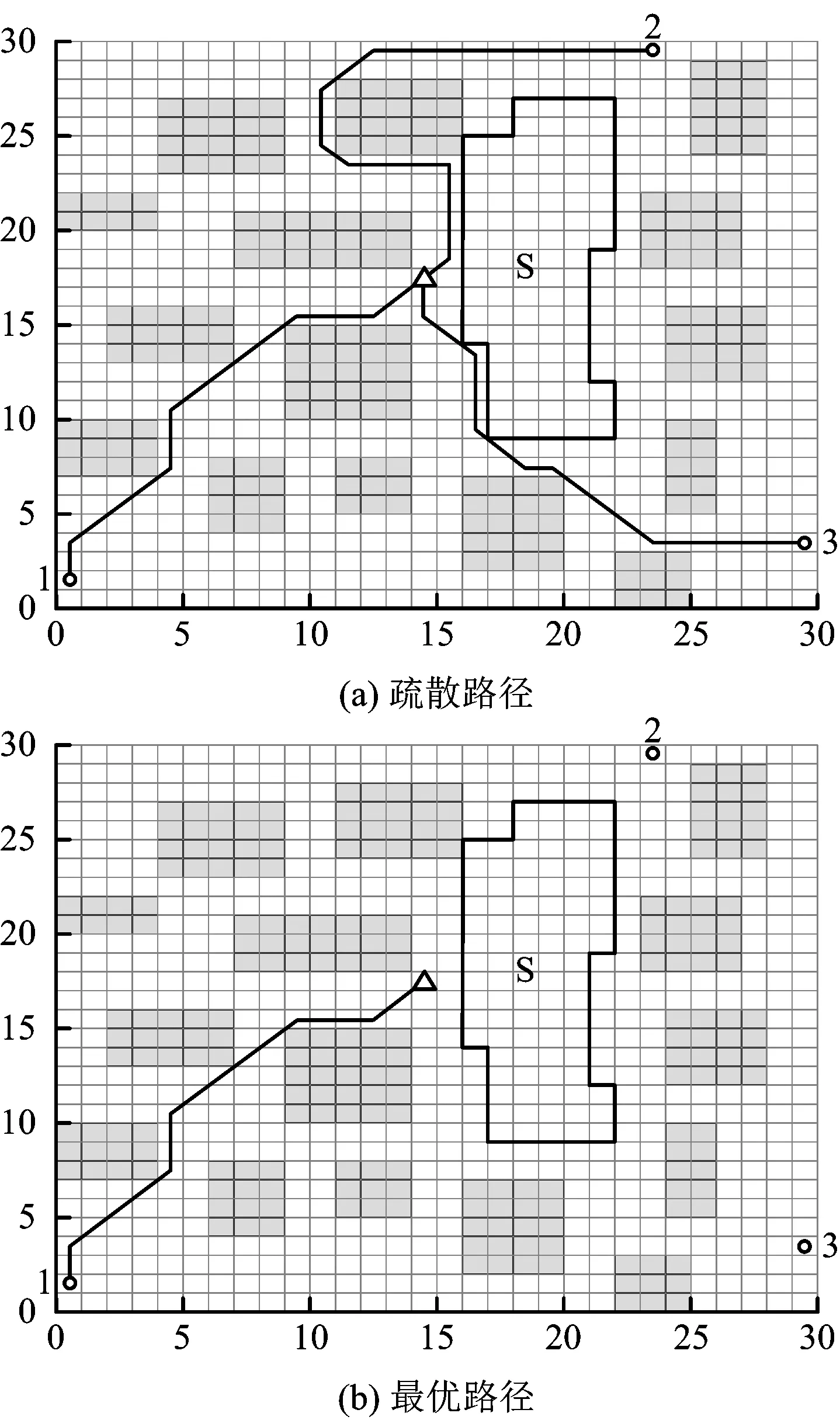
圖6 文獻[18]蟻群算法路徑圖Fig.6 ACO route maps of Literature[18]

3 結論

1)基于傳統蟻群算法，將火災條件下煙氣濃度及人員密度對疏散速度的影響與啟發函數η(t)耦合，建立了在火災條件下人員疏散路徑選擇模型。

2)得到優化模型參數組，使用該模型得到最優路徑，并將算法應用于多疏散出口問題，解決了最優路徑的選擇問題。采用可視化方法表示火場煙氣影響下的不同能見度，量化了不同煙氣濃度下對疏散速度的影響，并驗證了受煙氣影響較輕微的節點的可通過性，本文所建模型更加貼近真實火災環境，提高了全局疏散效率。