預測銑削穩定性的Hamming線性多步法

智紅英 ， 閆獻國， 杜 娟， 曹啟超

(1.太原科技大學 應用科學學院, 太原 030024； 2.太原科技大學 機械工程學院, 太原 030024)

在高速精密銑削加工過程中，再生顫振是一種常見的自激振動現象[1-2]，是引起加工過程失穩的主要因素[3]。因此，為了防止銑削加工過程中再生顫振的發生，加工前需要對銑削穩定性進行預測，以便在加工時獲得較高的表面質量，從而提高零件的精度。此外，考慮到再生顫振的銑削動力學模型可以近似地表示為時滯微分方程[4-5]，所以如何求解時滯微分方程才能精確且快速地獲得穩定性葉瓣圖是預測銑削穩定性的關鍵。

迄今為止，預測銑削穩定性的方法有很多種，主要分為實驗方法和數值方法，而數值方法主要有頻域法和時域法兩種。Budak等[6-7]提出了一種近似零階的半解析方法的頻域法求解銑削動力學方程，但這種方法無法滿足小徑向切深切削的計算精度。為了解決這個問題，Merdol等[8]提出了一種可以滿足小徑向切深的多頻域法。隨后，Insperger等[9-11]用時域法預測顫振穩定性，即半離散法(SDM)。該方法對銑削時滯微分方程中延遲項進行離散，其計算精度取決于離散步長。

基于這種方法，龍新華等人考慮了刀具與工件之間接觸效應的損失[12]和切削厚度變化相關的時間延遲效應[13]，李中偉等[14]提出了基于Magnus-Gaussian 截斷的銑削系統穩定性的改進的半離散法，Magnus-Gaussian截斷法比零階半離散法的收斂速度更快、計算時間更短。Butcher等[15-16]提出了Chebyshev多項式法和基于Chebyshev配點法來預測具有線性時滯微分方程銑削過程穩定性。為了提高計算精度和計算效率，Ding等[17-18]提出了全離散方法(FDM)，包括一階全離散法(1st-FDM)和二階全離散法(2nd-FDM)，這種方法是通過線性插值對狀態項和延遲項進行離散化處理。隨后，Guo等[19]在此基礎上通過牛頓插值提出了三階全離散法(3rd-FDM)，得出了具有比一階、二階全離散法更高的計算精度和更快的計算效率。Li等[20]提出了一種完全離散算法，這種方法是針對銑削穩定性預測的一種半解析算法。與半離散算法(SDM)和全離散算法(FDM)相比，此算法對時滯微分方程的各個部分都進行了離散化處理，簡化了離散化后迭代方程的復雜度。為了精確分離刀具自由振動時段和刀具-工件接觸過程中的強迫振動時段，Bayly等[21]提出了時域有限元分析方法，并具有較高的計算精度。Ding等[22]提出了一種數值積分法，這種方法是基于牛頓-柯特斯公式和高斯公式，通過直接離散積分方程中的積分項，構造出系統在單周期上的Floquet轉移矩陣用于預測銑削穩定性。Ding等[23]隨后又將有關數值積分法擴展為譜方法。在數值積分方法思想的指導下，Niu等[24]提出了一種廣義的龍格庫塔方法預測具有再生顫振的銑削穩定性。Li等[25]在經典的四階龍格庫塔的基礎上，基于完全離散法，提出了一種完全離散化的龍格庫塔方法預測銑削穩定性。Zhang等[26]基于辛普森公式提出了一種全新的方法預測銑削穩定性。Qin等[27]提出了一種基于亞當斯-莫爾頓的線性多步法預測銑削穩定性。Zhang等[28]根據泰勒公式，運用有限差分法和外推法，提出了一種數值微分法預測銑削穩定性。

隨著研究的不斷深入，越來越多的方法被用于預測銑削過程的穩定性。針對銑削加工動力學方程，提出了一種Hamming線性多步法預測銑削穩定性。

2 動力學模型

通過考慮再生顫振的動力學模型預測銑削穩定性，其動力學模型可由以下時滯微分方程描述：

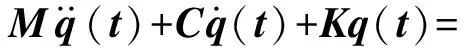
(1)

式中:M，C和K分別表示刀具的模態質量、模態阻尼和模態剛度矩陣；q(t)為刀具模態坐標，Kc(t)為周期系數矩陣，ap為軸向切削深度，T為時滯量且等于刀齒切削周期，T=60/(NΩ),N為刀具齒數，Ω為主軸轉速，單位為r/min。

令

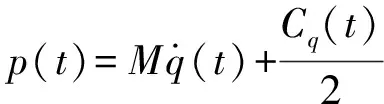
(2)

式(2)中，A0表示常數矩陣；A(t)表示周期為T的考慮再生效應的系數矩陣，且A(t)=A(t+T)。其中

(3)

單自由度和兩自由度系統主要區別是狀態向量x(t)、常數矩陣A0和周期矩陣A(t)的不同，下面將主要介紹這兩種動力學模型。

1.1 單自由度動力學模型

具有x方向的單自由度銑削加工動力學模型可由下列方程表示：

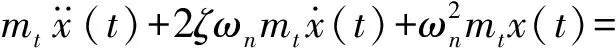
(4)

式中:mt,ζ,ωn分別表示刀具的模態質量、刀具的阻尼比、自然圓頻率；ap為軸向切削深度；T為時滯量且等于刀齒切削周期，即T=60/(NΩ)。h(t)由下列方程表示：

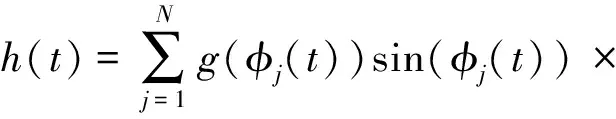
(5)

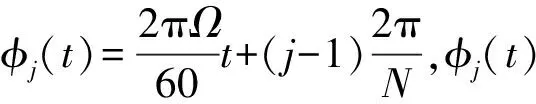
(6)

式中:φst和φex分別表示刀具的切入角和切出角。對于順銑，φst=arccos(2a/D-1),φex=π; 逆銑時，φst=0,φex=arccos(1-2a/D), 其中a/D表示為徑向切深與刀具直徑之比。

(7)

式(7)中

(8)

1.2 雙自由度動力學模型

在x和y方向上的雙自由度銑削動力學模型可由下列方程表示：

(9)

式(9)中周期系數矩陣Kc(t)可表示為：

(10)

其中：

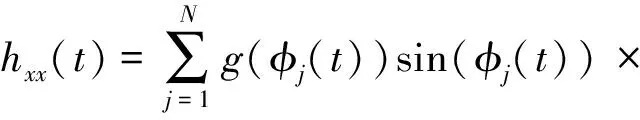
(11)

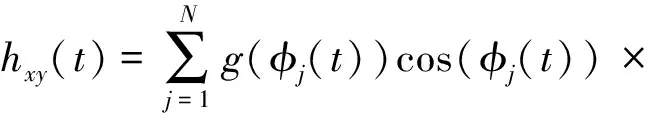
(12)

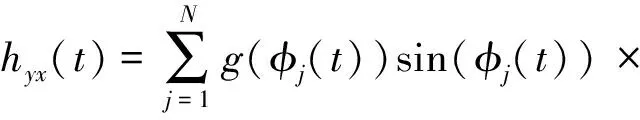
(13)

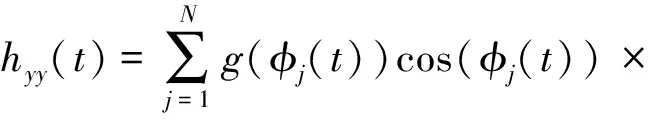
(14)

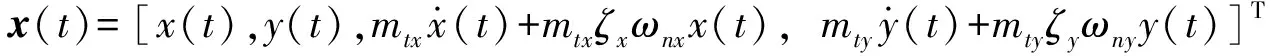
(15)

其中：

(16)

(17)

2 Hamming線性多步法(HAMM)

假設初始時刻為t0，通過空間狀態變換理論[17-18]，式(1)的解可由如下方程表示：

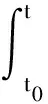
(18)

刀齒切削周期T可以劃分為自由振動時間間隔和tf強迫振動時間間隔T-tf。當刀具處于自由振動時刻t時，即t∈[t0,t0+tf]，狀態值有如下關系：

x(t)=eA0(t-t0)x(t0)

(19)

加工時刀具處于強迫振動時刻t時，即t∈[t0+tf,T], 將切削時間T-tf平均分成m個時間間隔，則每個時間間隔可表示為h=(T-tf)/m，相應的離散點表示為

ti=t0+tf+(i-1)h,i=1, 2, …,m+1

(20)

當t∈[ti,ti+1]時，方程(18)可以轉化為如下表達式：

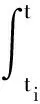
(21)

t=t1時，代入(19)式可得狀態量x(t1)和時滯量x(tm+1-T)之間的關系如下式表示：

x(t1)=x(t0+tf)=eA0·tfx(t0)=eA0·tfx(tm+1-T)

(22)

其余離散點x(ti)(i=2, …,m+1)可以通過線性多步法進行求解，為了簡化表達式，將A(ti)表示為Ai，x(ti)表示為xi，x(ti-T)表示為xi-T。

x2和x3利用Adams線性多步法[27]可以表示為：

(23)

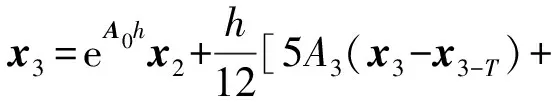
(24)

對式(23)、(24)分別化簡可得：

(25)

(26)

對于xi(i=4, 5, …,m+1)，用線性多步法中的Hamming公式來進行求解，則可表示為：

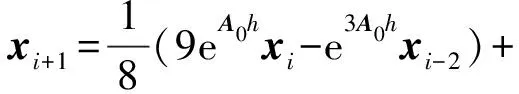
(27)

式(27)整理可得：

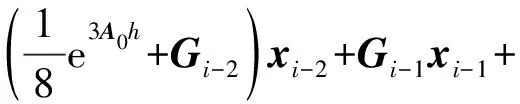
(28)

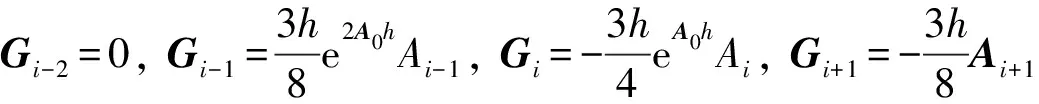
聯立式(22), (25), (26), (28)可得：

(29)

其中：

(30)

(31)

通過Hamming方法(HAMM)求得系統的狀態傳遞矩陣Φ為：

Φ=P-1Q

(32)

根據Floquet理論，當系統傳遞矩陣Φ特征值都小于1時，系統處于穩定狀態，否則，該系統則會進入顫振狀態。

3 數值仿真結果分析

3.1 收斂性分析

局部離散誤差的變化可以反映所提出方法收斂速度的快慢程度。通過理論上對局部離散誤差的分析，1st-SDM[10]和2nd-FDM[18]的局部離散誤差均為O(h3)，HAMM的局部離散誤差為O(h5)。利用Matlab軟件編程，在單自由度銑削動力學模型下對1st-SDM、2nd-FDM和HAMM三種方法的收斂性進行分析。切削參數為：徑向比a/D=1，切向力系數Kt=6×108N/m2，法向力系數Kn=2×108N/m2, 主軸轉速Ω=10 000 r/min和5 000 r/min，軸向切削深度ap==1.5 mm、1 mm、0.3 mm。模態參數采用與文獻[10]一樣的參數：逆銑，刀具齒數N=2，模態質量mt=0.039 93 kg，固有圓頻率wn=922×2π rad/s，固有阻尼ζ=0.011。

在1st-SDM、2nd-FDM和HAMM中，分別計算一個刀齒周期下不同離散數m所對應的狀態傳遞矩陣臨界特征值的模|μ|，局部離散誤差||μ|-|μ0||，而精確值|μ0|是m=500時采用1st-SDM得到的特征值的模。不同轉速和不同軸向切削深度下，1st-SDM、2nd-FDM、HAMM三種方法所對應的局部離散誤差如圖1所示。

由圖1可知，在不同的主軸轉速和軸向切削深度下，隨著離散數m的不斷增加，三種方法的局部離散誤差越來越接近于0。在離散數相同的條件下，HAMM的局部離散誤差要遠遠小于1st-SDM和2nd-FDM。

比如主軸轉速Ω=10 000 r/min，|μ0|=1.336 4 r/min，m=50時，1st-SDM的局部離散誤差為0.011 72，2nd-FDM的局部離散誤差為0.005 16，HAMM的局部截斷誤差為0.001 28，1st-SDM的局部離散誤差減少89%，比2nd-FDM的局部離散誤差減少75%。

此外還可以明顯地看出，HAMM的收斂速度均快于其它兩種方法，主軸轉速越高，離散數少的HAMM能達到離散數較多的1st-SDM和2nd-FDM的局部離散誤差，和理論分析結論一致。因此，在相同的局部離散誤差下，HAMM計算所用的時間遠遠少于1st-SDM和2nd-FDM。

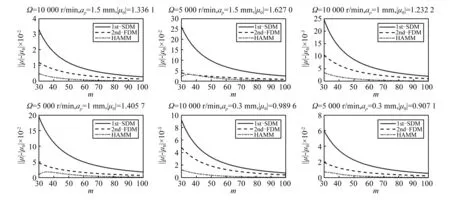
圖1 1st-SDM、2nd-FDM、HAMM三種方法收斂速度的比較Fig.1 Convergence rate comparisons of1st-SDM, 2nd-FDM and HAMM

3.2 穩定性葉瓣圖

3.2.1 單自由度銑削模型

在單自由度銑削模型中，為了比較1st-SDM、2nd-FDM和HAMM這三種計算方法的準確性，將模態參數設置與2.1節相同。徑向比a/D=1, 0.1, 0.05，主軸轉速為5 000≤Ω≤10 000 r/min，并設置200個等間距的轉速；軸向切削深度0≤w≤10 mm，并設置100個等間距切削深度，則銑削穩定性葉瓣圖便構成了200×100的網格。設離散數m為30、40，通過2.1節可知，HAMM計算速度快，具有較高階的誤差，故將HAMM離散數m=200時所得的穩定性葉瓣圖作為理想參考曲線。在不同離散數值和不同徑深下，三種方法所得的穩定性葉瓣圖與理想參考曲線的對比如圖2～4所示。

由圖2～4可知，在單自由度銑削模型下，在同種方法中，隨著離散數m的增加，三種方法的計算精度都有所提高，都更接近理想參考曲線，當離散數m相同時，HAMM的計算精度要優于1st-SDM和2nd-FDM的計算精度。

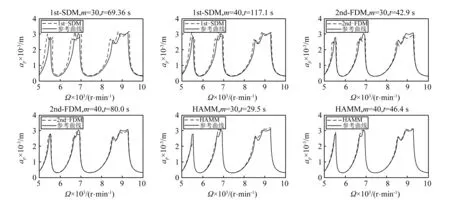
圖2 單自由度銑削模型a/D=1下1st-SDM、2nd-FDM、HAMM三種方法的穩定性葉瓣圖Fig.2 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a single degree-of-freedom milling model with a/D=1

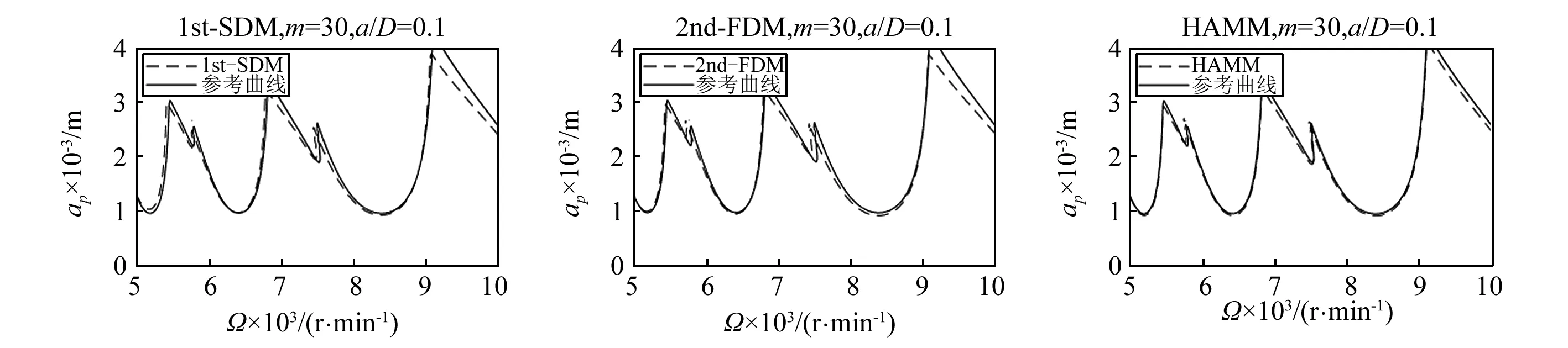
圖3 單自由度銑削模型a/D=0.1下1st-SDM、2nd-FDM、HAMM三種方法的穩定性葉瓣圖Fig.3 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a single degree-of-freedom milling model with a/D=0.1

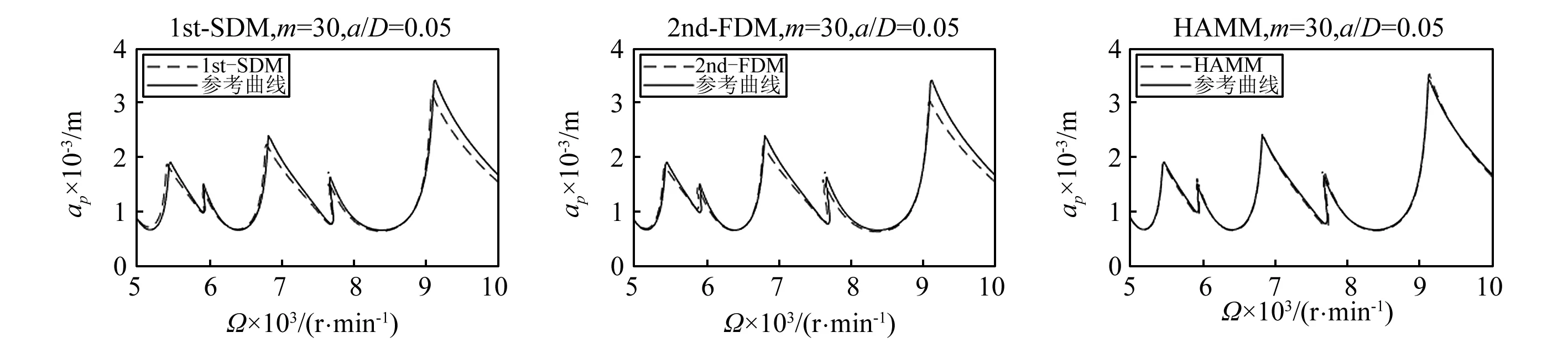
圖4 單自由度銑削模型a/D=0.05下1st-SDM、2nd-FDM、HAMM三種方法的穩定性葉瓣圖Fig.4 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a single degree-of-freedom milling model with a/D=0.05

在圖2中，當m=30時，1st-SDM的計算時間為69.36 s，2nd-FDM的計算時間為42.9 s，HAMM的計算時間為29.5 s，比1st-SDM所用時間縮短57.6%，比2nd-FDM所用時間縮短31.2%。當m=40時，1st-SDM的計算時間為117.1 s，2nd-FDM的計算時間為80 s，HAMM的計算時間為46.4 s，比1st-SDM所用時間縮短60.3%，比2nd-FDM所用時間縮短42%。

在圖3，圖4中可以看出，在離散數m相同時，當徑向比a/D比較小時，HAMM方法計算精度遠遠高于1st-SDM和2nd-FDM。故HAMM是一種較優的預測銑削穩定性的計算方法。

3.2.2 雙自由度銑削模型

雙自由度銑削過程的系統參數與單自由度的參數相同。設刀具浸入比a/D=0.1，離散數m=10和20，主軸轉速Ω從5 000 r/min到20 000 r/min，軸向切削深度ap從0～10 mm，穩定性葉瓣圖的網格設置為200×100，將m=200時由HAMM進行數值計算得出的穩定性葉瓣圖作為理想參考曲線，三種方法的穩定性葉瓣圖與理想參考曲線的對比圖，如圖5所示。

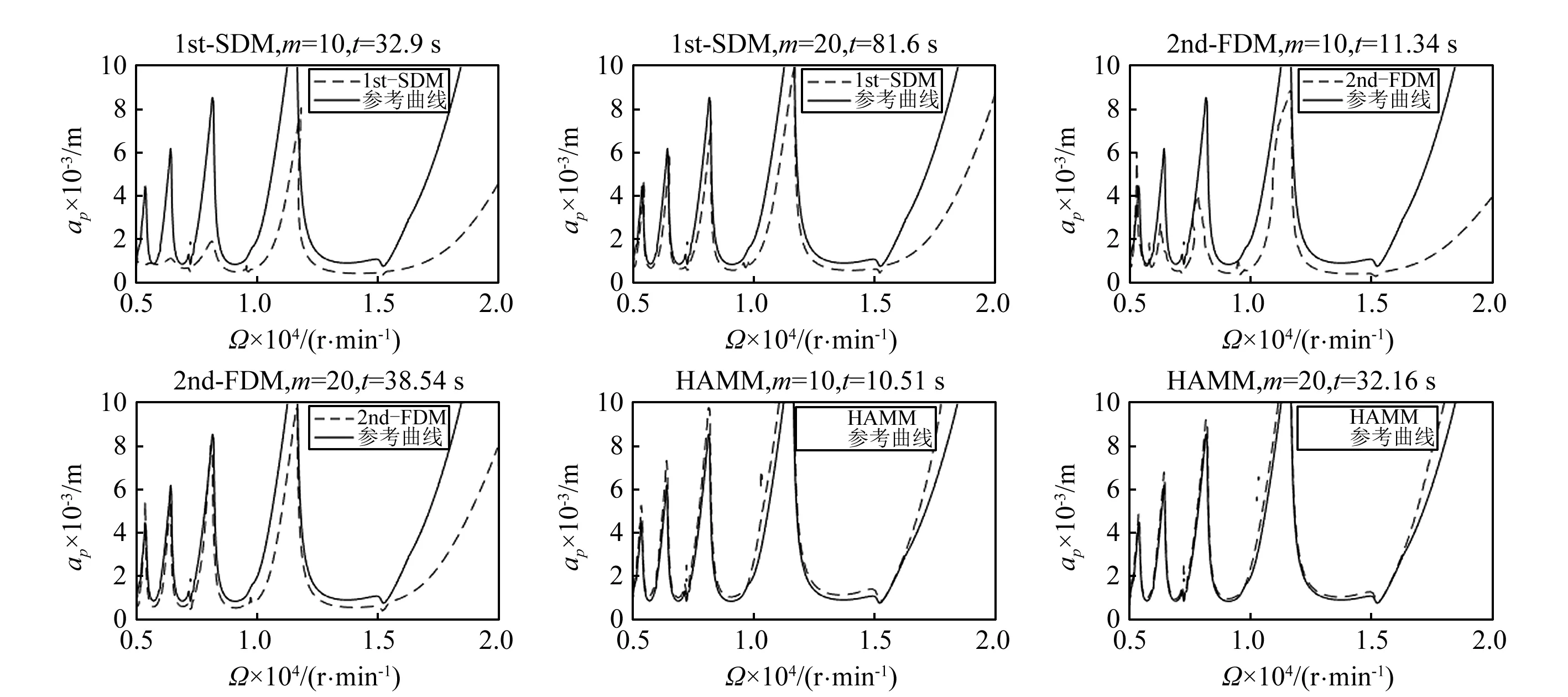
圖5 雙自由度銑削模型下1st-SDM、2nd-FDM、HAMM三種方法的穩定性葉瓣圖Fig.5 Stability lobe diagrams of1st-SDM, 2nd-FDM and HAMM for a double degree-of-freedom milling model

由圖5可以看出，在同種方法中，隨著離散數的增加，三種方法的計算精度都有所提高；當離散數m相同時，HAMM的計算精度遠遠高于1st-SDM和2nd-FDM。舉個例子來說，當m=10時，1st-SDM的穩定性葉瓣圖和理想參考曲線間產生了明顯的偏差，2nd-FDM的穩定性葉瓣圖雖然降低了和參考曲線間的偏差，但還是存在明顯的不同之處，而HAMM的穩定性葉瓣圖幾乎和理想參考曲線一致。

當m=10時，1st-SDM的計算時間為32.9 s，2nd-FDM的計算時間為11.34 s，HAMM的計算時間為10.51 s。當m=20時，1st-SDM的計算時間為81.64 s，2nd-FDM的計算時間為38.54 s，HAMM的計算時間為32.16 s，因此，在離散數相同時，HAMM的計算效率和2nd-FDM相當，遠遠高于1st-SDM。故HAMM是一種具有較高的計算精度和較快的計算效率的預測銑削穩定性的方法。

4 實驗驗證

針對提出的用于預測銑削穩定性的HAMM算法，本節通過實驗來進行驗證。本次驗證實驗所用機床為五軸立銑加工中心DMU60monoBLOCK,所用銑刀為整體式硬質合金4刃刀具，直徑為12 mm，刀長為75 mm。被加工工件材料為航空鋁合金AL7075,實驗采用無冷卻液的干式切削。試驗現場，如圖6所示。

圖6 試驗現場Fig.6 Testing site

在切削鋁合金工件的過程中，切削參數為：徑向比a/D=1，切向力系數Kt=6×108N/m2，法向力系數Kn=2×108N/m2，主軸轉速為3 000 r/min，3 500 r/min，4 000 r/min，4 500 r/min和5 000 r/min，軸向切削深度為0.4 mm，0.8 mm，1.2 mm，1.6 mm，2.0 mm。模態參數由模態錘擊試驗獲得：逆銑，刀具齒數N=4，模態質量mt=0.1 kg，固有圓頻率ωn=9 420 rad/s，固有阻尼比ζ-0.029 81。

選用不同的主軸轉速和軸向切削深度進行切削，利用激光測振儀搜集振動信號，并利用統計方法進行分析得穩定點和不穩定點。基于HAMM法預測銑削穩定性的有效性,結合實驗參數,計算機仿真結果和試驗結果，如圖7所示。

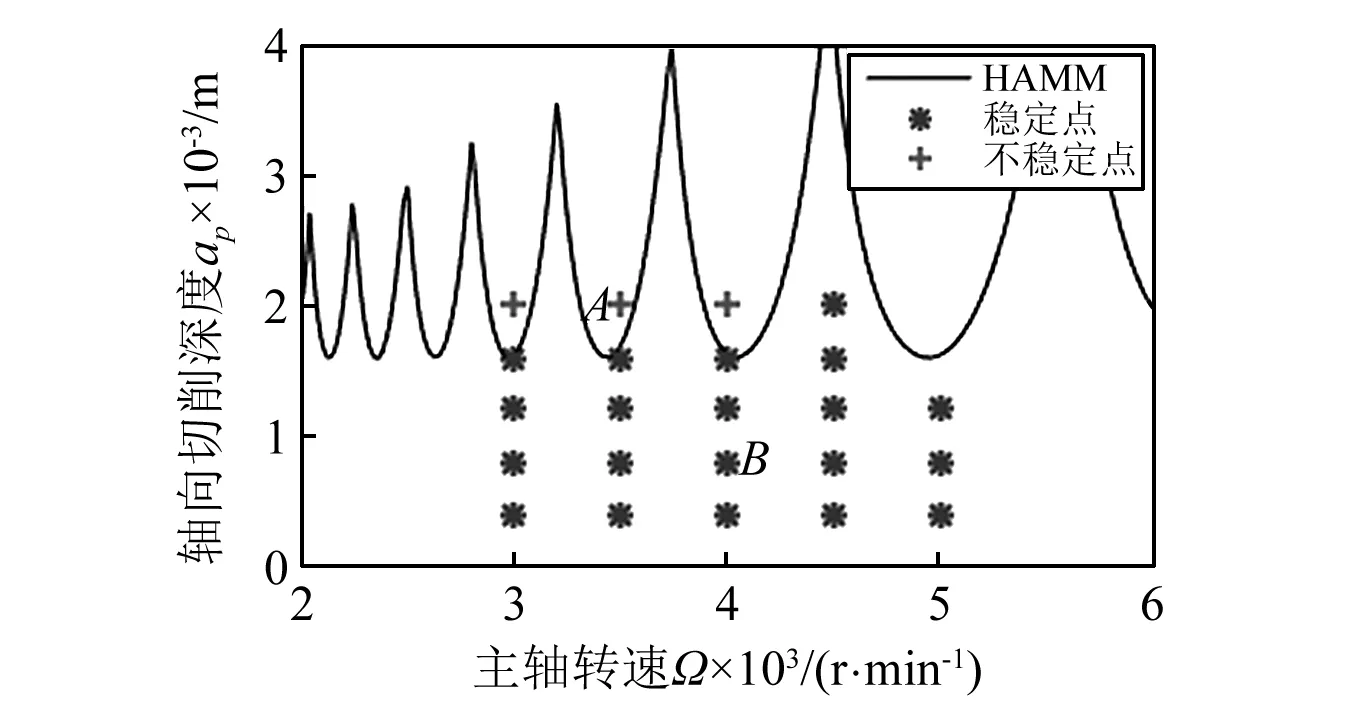
圖7 HAMM法的計算機仿真結果和實驗結果Fig.7 Computer simulation and experimental results of HAMM method

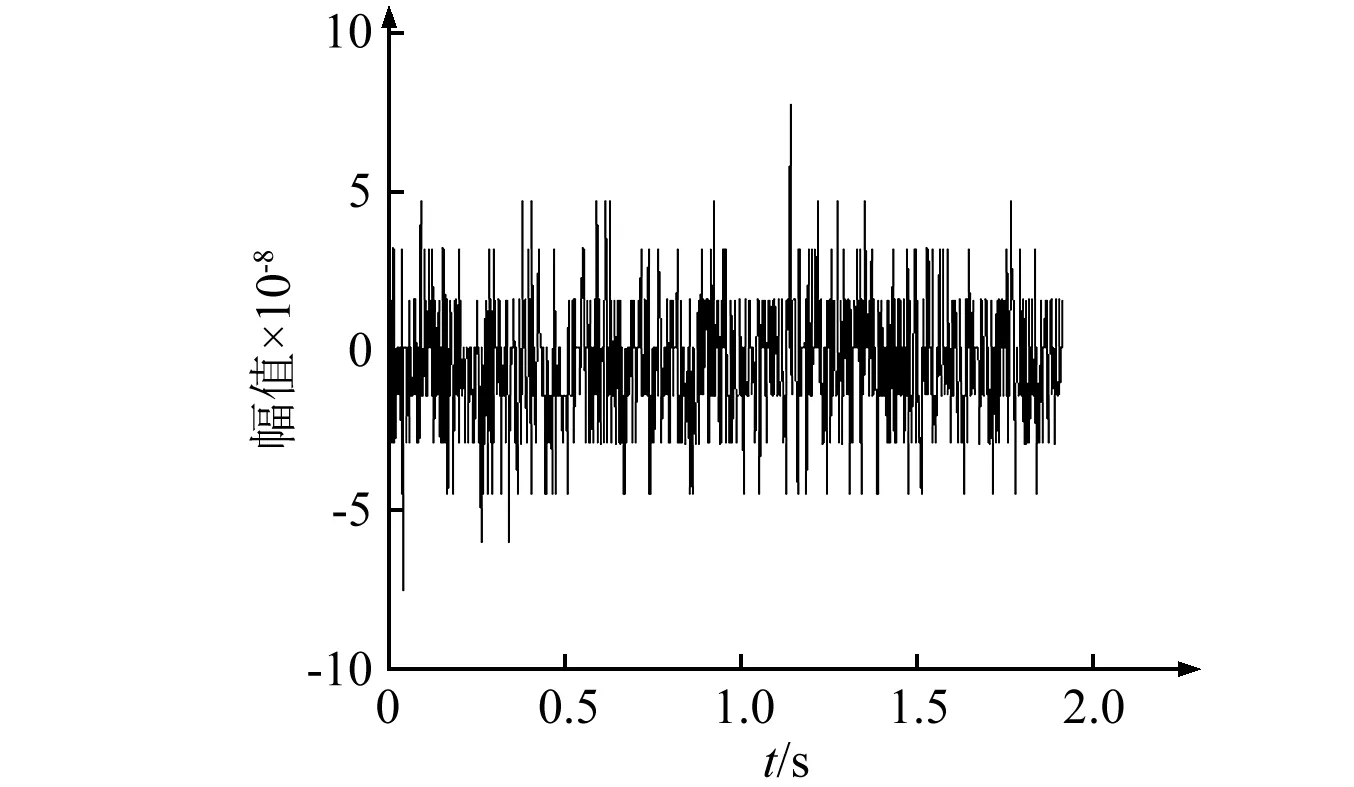
圖8 穩定點B的時域圖Fig.8 Time-domain diagram of stability point B

穩定點B的時域圖如圖8。

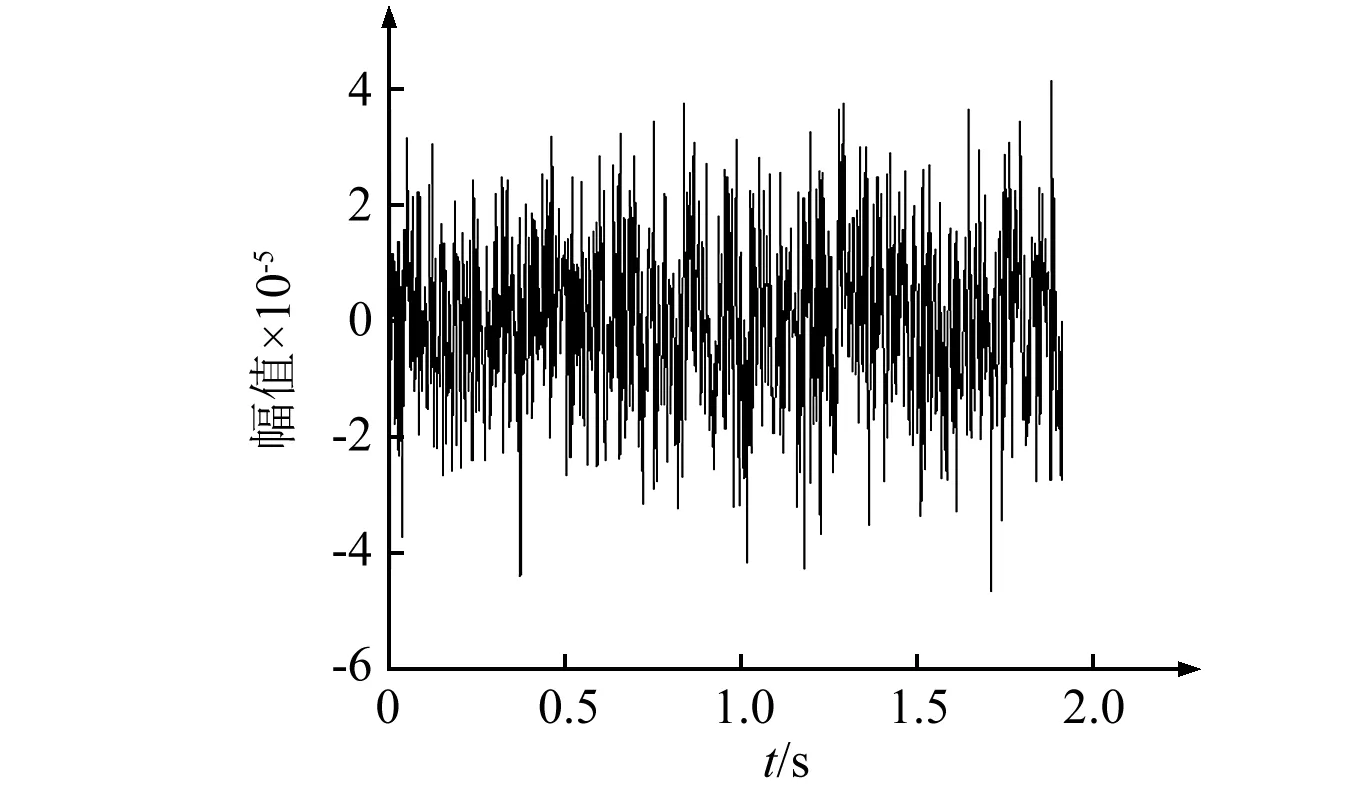
圖9 不穩定點A的時域圖Fig.9 Time-domain diagram of unstability point A

不穩定點A的時域圖如9。

由圖7可以看出，HAMM方法的計算機仿真結果和實驗結果是吻合的，進一步說明HAMM方法是一種有效的預測銑削穩定性的方法。

5 結 論

針對銑削動力學模型，提出了HAMM預測銑削穩定性。通過以上研究，得到如下一些結論：

通過對局部離散誤差的分析可知，HAMM的收斂速度比1st-SDM和2nd-FDM快得多。主軸轉速越高，離散數少的HAMM能達到離散數較多的1st-SDM和2nd-FDM的局部離散誤差，和理論分析結論一致。

無論是在單自由度還是雙自由度銑削模型中，從所給的三種方法的穩定性葉瓣圖中可以得出，隨著離散數的增加，三種方法的計算精度都有所提高。當離散數相同時，HAMM的計算精度高于1st-SDM和2nd-FDM。特別是在雙自由度銑削模型下，HAMM的計算精度遠遠高于1st-SDM和2nd-FDM。在離散數相同的條件下，HAMM的計算效率和2nd-FDM相當，遠遠高于1st-SDM。

HAMM是一種較優的預測銑削穩定性的方法，它具有較高的預測精度和較快的計算效率。實驗驗證表明，HAMM方法用來預測銑削穩定性是有效的。

DOI:10. 1007/s00170-016-8708-z.