正切型非線性包裝系統跌落沖擊響應分析的同倫攝動法與修正

郭蓓蓓， 王 軍,2

(1. 江南大學 機械工程學院，江蘇 無錫 214122； 2. 江蘇省先進食品裝備制造技術重點實驗室，江蘇 無錫 214122)

非線性包裝系統常常由于緩沖材料的非線性或實際阻尼的存在而使系統表現為強非線性，使得問題的理論分析解非常困難。在包裝工程領域，緩沖包裝材料的非線性常表現為三次、正切、雙曲正切型等。而系統的動力學響應分析處理一般采用數值分析方法，該方法簡單可操作，但只能得到系統響應散點圖其無法確切描述系統在任意瞬時的運動狀態，且難以明確表示跌落沖擊持續時間。

對于非線性問題近似解析解的求解，變分迭代法(Variational Iteration Method, VIM)[1-6]、攝動法[9-11]、何氏頻率-振幅關系(HFAF)[12]、同倫分析法[8]等嘗試較多。其處理問題各有優缺點，但都計算較復雜耗時。通常攝動法是指在簡單問題的解附近求解困難問題級數解的方法，其系統運動方程含有小參數ε，方程的解會依賴參數ε。小參數的選擇成為了至關重要的問題，選擇得當，可達到理想結果，若選擇不當，結果反之。而同倫攝動法[13-18]不依賴任何小(或者大)參數，而是應用同倫技術構造一個含嵌入參數q∈[0,1]的方程，然后把嵌入參數作為小參數，這樣既可以克服傳統攝動理論的不足，又可以充分應用各種攝動方法。方程的近似解可以寫成一系列無窮級數相加的形式，并且這個級數和收斂于它的精確解，其結果顯示該方法是一種更有效，更具一般性的分析手段。

緩沖包裝設計中，通常需要對產品樣品進行多次跌落測試，試驗可重復性差。而最大加速度響應是評價緩沖包裝有效性的一個重要指標。為了減少試驗次數更好的保護樣品，可以對樣品進行安全高度(低高度)的跌落試驗來預測目標跌落高度(較大高度)下產品的響應加速度，那么緩沖包裝動力學方程的理論解析解求解是至關重要的一步。本文以正切型非線性包裝系統跌落沖擊為例，采用同倫攝動法對動力學方程進行求解并結合能量法對結果進行修正得到其一階近似解析解，證明同倫攝動法的簡單有效性。

1 攝動法的基本思想

選取非線性代數方程

A(x)=0

(1)

引入嵌入變量q∈[0,1]， 分別選取輔助線性算子L(u)和非線性算子N(u)， 將方程(1)轉換如下

L(u)+N(u)=0

(2)

構造一個同倫函數H(u,q):Ω×[0,1]→R, 滿足

(3)

式中：q∈[0,1]為嵌入變量，x0是原方程(1)的初始解，并且滿足邊界條件。 當q=0時

H(u,0)=L(u)-L(x0)=0

(4)

當q=1時

H(u,1)=N(u)+L(u)=0

當q從0變換到1時，H(u,q)從初始解u0(t)變換到u(t)， 把q當做小參數， 方程的解表達成q的冪級數

u=u0+qu1+q2u2+…

(6)

當q=1時， 方程的解為

(7)

2 能量法的基本思想

在非線性系統的跌落沖擊問題分析中，通常使用能量法(EM)來得到系統的最大位移和最大加速度，但是難以得到系統響應的周期和時間歷程。對于非線性系統的跌落沖擊問題，若不考慮系統阻尼，理想情況下，當緩沖材料變形達到最大值xm時， 系統的重力勢能將全部轉化為彈性勢能。假設包裝系統的跌落高度為h，產品重量為W，系統的重力勢能表達如下

U=Wh

(8)

對于非線性包裝系統，f(x)指恢復力， 是且僅是x的非線性函數。根據能量法，有

(9)

3 正切型非線性包裝系統的響應求解

3.1 包裝系統的同倫攝動法求解

對于正切型非線性包裝系統，若不考慮阻尼的影響，系統跌落沖擊動力學方程和初始條件如下

(10)

(11)

進行泰勒展開并取前三項

(12)

這樣將正切型非線性方程轉化成高階非線性微分方程

(13)

(14)

(15)

對于上式方程及初始條件，采用如下的線性及非線性算子

(16)

其中，

g(u)=ku3+bu5

(17)

構造如下同倫

H(u,q)=L(u)-L(x0)+q[N(u)+L(x0)]=0

(18)

0≤q≤1, 把q當做小參數， 解表示為q的冪級數形式

u=u0+qu1+q2u2+…

(19)

將解的表達式代入方程如下

L(u0+qu1+q2u2+…+qnun)-L(x0)+
q[N(u0+qu1+q2u2+…+qnun)+L(x0)]=0

(20)

令q的同次冪的系數相同

(21)

(22)

求解上式得

u0=x0=Asinωt

(23)

同時方程(21)變為

(24)

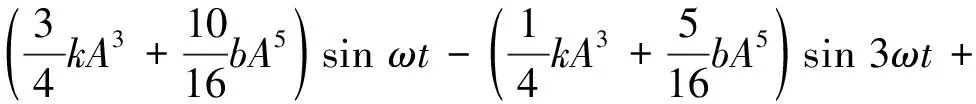
(25)

將上式代入式(24)得

(26)

令

u1=Bsint+Csinωt+Dsin 3ωt+Esin 5ωt

(27)

(28)

(29)

聯立式(1)和式(2)，采用待定系數法求解參數

(30)

為了消除長期項，令

(31)

解得

(32)

所以方程的位移近似解為

(33)

(34)

對上式求一階及二階導得方程的速度及加速度解析式如下

(35)

(36)

為了分析比較方程近似解精度，取參考文獻[3]中的參數做參考分析精度，這樣不僅可以更好的分析同倫攝動法精度，也易將其與其他非線性分析方法結果進行優缺點比較。其中：m=10 kg,h=0.6 m,k0=600 N/cm,r=72 N/cm3,a=0.000 1 N/cm5。

結合初始條件，得到振幅A=3.196 cm， 頻率ω=107.32 s-1。

表1 正切型非線性系統HPM算法和能量法修正與Runge-Kutta算法的結果對比Tab.1 Comparison of solutions obtained by HPM and CHPM(E) with that of Runge-Kutta method for the tangent nonlinear system

3.2 能量法修正算法

利用能量法對同倫攝動法結果進行修正，如下

(37)

最大位移可通過下式計算

(38)

圖1和圖2分別表示正切型非線性包裝系統的HPM算法及CHPM算法的位移響應和加速度響應與Runge-Kutta算法結果的對比圖，由圖1知，HPM算法及CHPM算法的位移曲線基本與Runge-Kutta法結果吻合，修正后誤差更小。由圖2得，HPM與Runge-Kutta法的最大加速度誤差相差較明顯，但CHPM結果曲線卻與Runge-Kutta法高度吻合，說明修正后的結果更滿足工程要求。

圖1 正切型非線性系統HPM和能量法修正與Runge-Kutta算法位移響應對比Fig.1 Comparison of the displacement response by HPM and CHPM (energy method) with the numerical simulation solved by the Runge-Kutta method for the tangent nonlinear system

圖2 正切型非線性系統HPM和能量法修正與Runge-Kutta算法加速度響應對比Fig.2 Comparison of the acceleration response by HPM and CHPM (energy method) with the numerical simulation solved by the Runge-Kutta method for the tangent nonlinear system

4 結 論

緩沖包裝系統是對各種實際緩沖包裝件的抽象，它對外部沖擊和振動等作用的響應是進行緩沖包裝設計的理論依據，研究包裝系統跌落沖擊問題的最大位移和最大加速度顯得尤為重要。本文采用同倫攝動法與能量法的結合研究了正切型非線性包裝系統的跌落沖擊響應問題，并與Runge-Kutta法比較，結果表明該算法具有足夠的精度，可以滿足一般工程需要，同時證明同倫攝動法不僅可以有效解決非線性振動問題，同時也為解決跌落沖擊問題提供了新思路。