某乘用車整車怠速抖動控制研究

程 林， 劉啟華， 趙文杰， 劉 濤， 姜耀全， 張小虎， 盧伯聰

(上海汽車集團股份有限公司技術中心，上海 201804)

隨著經濟水平的提升和生活品質的改善，人們對于汽車考量的不僅是外觀、動力、油耗、排放、安全等傳統因素，很大程度上也離不開駕乘感、舒適性等主觀因素。在整車性能指標中，NVH性能已經成為用戶敏感度最高的指標之一[1]。隨著汽車保有量的增加，交通堵塞狀況日益嚴重，整車在怠速工況下的時間量顯著增多，人們對于怠速狀態下汽車的舒適性要求也隨著提高。汽車怠速時人們最直觀的感受就是整車的振動水平，若振動過大，就會造成明顯的市場抱怨。許多主機廠的售后問題都與怠速抖動有關，抖動水平直接影響客戶評價。整車怠速抖動不但容易引起客戶的不舒適感，而且會造成零部件振動過大，壽命降低，因此整車怠速抖動問題的研究與優化具有較大的實際意義。

本文針對某整車怠速抖動問題，先是通過NVH測試方法分析抖動頻率特征，然后通過模態分析方法進行動力總成懸置系統剛體模態試驗，確認抖動根本原因，再應用整車16自由度CAE模型進行參數敏感度分析，進行懸置剛度參數優化，成功降低該整車的怠速抖動量級，對于整車怠速抖動問題的解決方法具有一定的參考意義。

1 整車怠速抖動問題

1.1 基本描述

整車怠速抖動問題，普遍采用主觀評估和客觀測試相結合的方法[2]。本文故障車冷車起動時，怠速轉速較高(約1 100 r/min)，沒有明顯的抖動問題；隨著水溫的升高，發動機轉速逐漸降低，車內抖動增加明顯；完全熱機后(約700 r/min)，抖動量級較大且持續存在，易引起抱怨。

1.2 振動頻譜分析

在駕駛員座椅導軌處布置振動傳感器進行測試(采用整車坐標系，汽車前后方向為X，左右側向為Y，豎直向上為Z)，測試結果顯示-抖動頻率為11.3 Hz。該型車怠速時，發動機熱機轉速680 r/min，發動機運轉一階頻率為11.33 Hz，與抖動頻率吻合。從振動頻譜圖中看出，座椅導軌X向振動最大，Z向振動其次(Y向量級較小，略)，如圖1所示。

圖1 座椅導軌怠速振動頻譜Fig.1 Spectrum of seat rail idle vibration

通常，對于整車怠速抖動這樣的系統問題，需要分析振動源和傳遞路徑[3]。首先分析振動源，動力總成是整車怠速時的主要振動激勵源，發動機曲軸回轉系統及變速箱輸入軸系統的旋轉不平衡是產生一階振動激勵的因素之一；發動機燃燒不均勻性是產生一階激勵的第二個因素。它們均對發動機本體施加相應的激勵力，產生本體振動響應，進而通過懸置產生力作用在車身上，再進一步傳遞到車內，表現為整車怠速抖動現象。在發動機本體上布置振動傳感器進行測試(整車坐標系)，結果如圖2所示。發動機的振動能量主要集中在二階，符合四缸機正常工作燃燒時的二階振動，一階振動沒有明顯異常，由此判斷該車抖動問題主要受結構傳遞路徑的影響。對于動力總成旋轉不平衡激勵和燃燒不穩定性激勵的機理和優化方法，將另文深入剖析。

圖2 發動機怠速振動頻譜Fig.2 Spectrum of engine idle vibration

2 懸置系統試驗分析

2.1 剛體模態基本原理

動力總成懸置系統是動力總成隔振性能的關鍵環節[4]。對于怠速抖動等低頻問題來說，安裝動力總成的幾個懸置顯然是最主要的結構傳遞路徑，因此需要對懸置系統進行分析，以進一步判斷問題原因。該車動力總成采用三點懸置，可以把動力總成懸置系統視為一個具有三個彈性支撐的質量-剛度系統[5]。這個系統有六個自由度，分別為沿三軸方向的平動x，y，z和繞三軸方向的轉動θx，θy，θz，系統六自由度坐標為：

[q]=[xyzθxθyθz]T

(1)

根據拉格朗日定理和虛功原理，可得懸置系統動力學方程為：

(2)

式中:[M]為質量矩陣;[C]為阻尼矩陣;[K]為剛度矩陣;F(t)為激勵力。

2.2 動力總成懸置系統剛體模態

一般動力總成懸置系統剛體模態頻率在5～30 Hz之間，較易與發動機低階激勵耦合，懸置是否合理設計關系到整車對動力總成激勵的敏感程度。采用試驗模態方法測試各個測點加速度響應，并提取模態參數[6-7]。結果如表1所示。模態振型如圖3～8所示。

表1 動力總成懸置系統剛體模態

圖3 第一階模態振型Fig.3 The first mode

圖4 第二階模態振型Fig.4 The second mode

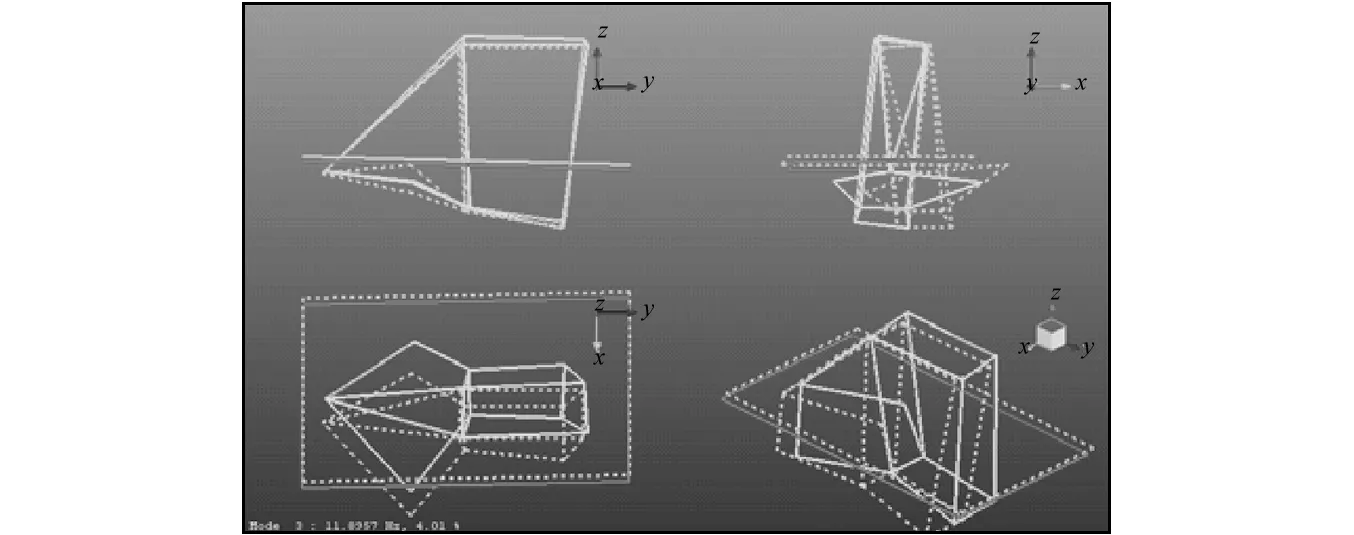
圖5 第三階模態振型Fig.5 The third mode

圖6 第四階模態振型Fig.6 The fourth mode

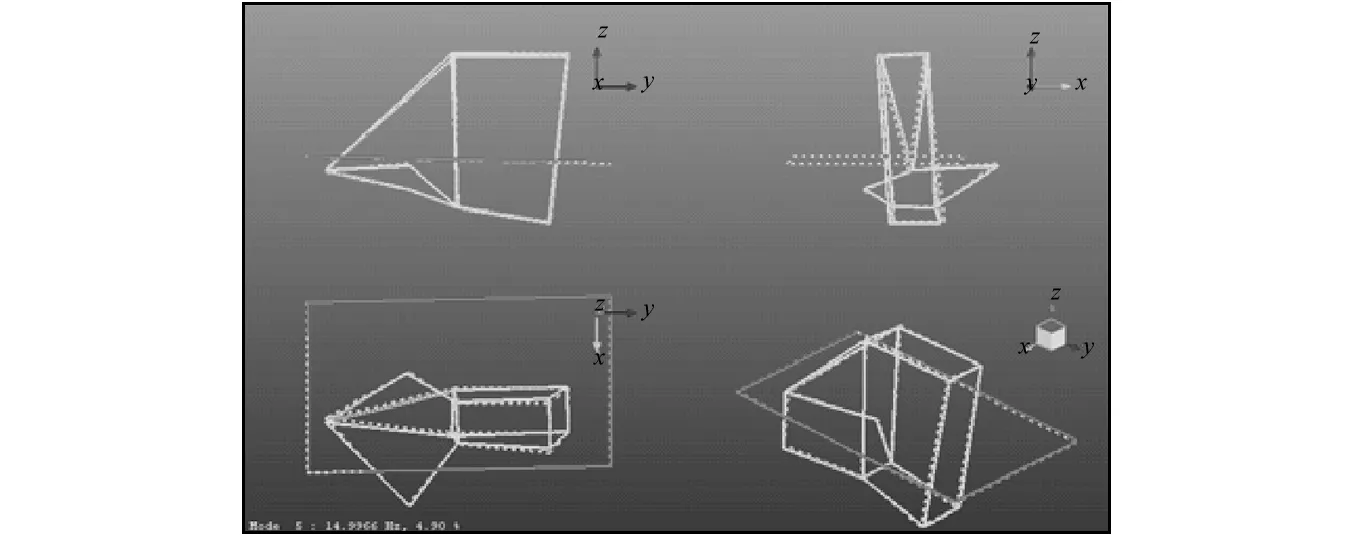
圖7 第五階模態振型Fig.7 The fifth mode

圖8 第六階模態振型Fig.8 The sixth mode

從結果中可以看出，Z向平動(Bounce)對應的第2階剛體模態和X向平動(Fore-aft)對應的第3階剛體模態這兩個模態本身就比較接近，可能引起這Z向和X向這兩個方向對應模態間的耦合。整車怠速下動力總成激勵的一階振動分量11.3 Hz，與Z向平動模態10.9 Hz和X向平動模態11.9 Hz均非常接近，極易引起耦合共振，從而造成整車抖動。從前面的分析可知，整車抖動時最顯著的方向也是Z和X這兩個方向。據此可以判斷，該整車怠速抖動問題是由于懸置系統剛體模態與動力總成一階振動分量耦合共振。

3 整車系統CAE分析

3.1 整車16自由度模型

懸置系統需要重新設計匹配來避開模態共振，一般改變懸置的安裝位置、角度或剛度[8]。對于量產車來說，改變懸置的安裝位置、角度顯然相當困難，比較可行的是改變懸置的剛度。目前整車普遍采用三點或四點懸置，每個懸置有三個剛度方向參數，涉及變量較多。因此需要需要合理配置懸置參數，降低振動耦合度[9]。本文通過CAE仿真手段建立模型計算整車怠速抖動，基于懸置剛度偏差進行DOE仿真分析，同時對各個剛度參數進行敏感度分析，以確定每個方向剛度參數對于怠速抖動的影響程度。整車16自由度剛體模型如圖9所示。

圖9 整車16自由度CAE模型Fig.9 CAE model of vehicle with 16 freedoms

3.2 懸置剛度敏感度分析

該整車采用三點懸置，分別為發動機懸置，變速箱懸置和下系桿懸置，以懸置剛度為輸入，以座椅導軌振動為輸出。設定DOE工況輸出限值如下：

f(K1,K2,K3)≤0.005

(3)

[Ki](Kix,Kiy,KiZ),i=1,2,3

(4)

式中:K1x,K1y,K1Z分別為發動機懸置三個方向剛度，K2x,K2y,K2Z分別為變速箱懸置三個方向剛度，K3x,K3y,K3Z分別為下系桿懸置三個方向剛度。

每個懸置3個方向共計9個變量，以這9個剛度變量為輸入，共512個工況，以剛度上下浮動20%為設計因素變化量進行DOE計算，基于DOE結果對于各懸置三個方向剛度參數進行敏感度分析。設置懸置剛度與座椅導軌振動的關聯程度方程如下：

(5)

式中:Rab表示關聯程度;a為懸置剛度;b為座椅導軌振動。

由關聯度計算可知，懸置剛度對座椅導軌振動的敏感度排序依次是下系桿懸置X向剛度，發動機懸置Z向剛度，變速箱懸置Z向剛度。座椅導軌兩個方向振動與懸置剛度的關聯度結果分別如表2和表3所示。

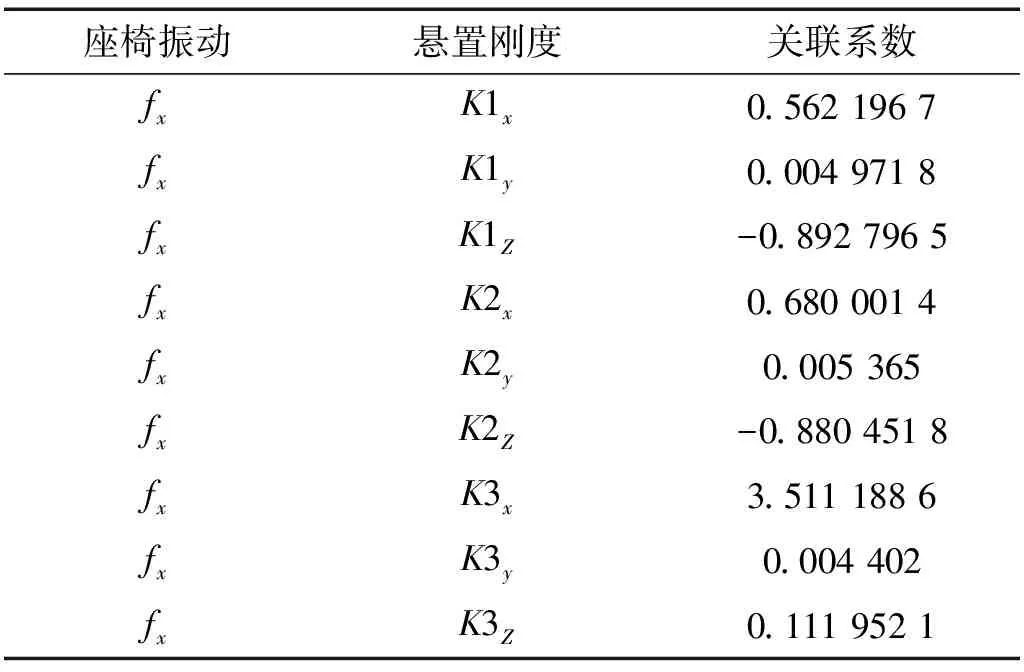
表2 座椅導軌X向振動與懸置剛度的關聯度

表3 座椅導軌Z向振動與懸置剛度的關聯度

4 試驗驗證及結論

4.1 試驗驗證

在滿足性能指標的前提下，敏感度高的設計變量應盡可能保持在最優值附近，設計、制造都要從嚴要求[10]。基于懸置剛度參數敏感度分析結果，控制下系桿X向剛度、發動機懸置Z向剛度和變速箱懸置Z向剛度在懸置零部件偏差在設計中值附近，對于三個懸置進行剛度優化。將改進后的懸置裝車后進行試驗驗證，發現整車怠速抖動明顯下降。客觀測試顯示，座椅導軌一階抖動抱怨的頻率亮帶基本消失。優化后座椅導軌怠速振動如圖10所示。

圖10 優化后座椅導軌怠速振動Fig.10 Idle vibration of seat rail after optimization

對于懸置剛度優化后的車輛進行實車主觀評估，以驗證實際改善效果。實車怠速工況主觀評估結果如表4所示。

表4 怠速工況主觀評估結果

由上述可知，懸置剛度優化對于怠速工況振動有明顯改善，但不確定優化后對于瞬態工況(特別是加速工況)的影響，因此還有必要評估下優化對于其他工況整車振動的影響。該車為自動擋，僅需評估D擋加速。D擋加速工況主觀評估結果如表5所示。結果表明，優化對于其他工況整車振動無惡化。

表5 D擋加速工況主觀評估結果

4.2 結 論

(1)運用模態測試方法獲取動力總成懸置系統的剛體模態信息，分析怠速抖動原因，為類似怠速抖動問題研究提供了思路。

(2)采用CAE仿真手段建立整車16自由度剛體模型，針對懸置剛度參數進行敏感度分析，為怠速抖動優化提供了方向。

(3)將剛度參數優化后的懸置裝車驗證，發現優化后怠速抖動明顯改善，對于整車怠速抖動問題的解決具有參考價值。