有效指導分析策略 提升問題解決能力

康莉 郭曉倩

中圖分類號：G623.5 文獻標識碼：B 文章編號：1672-1578（2018）33-0116-02

“問題是數學的心臟，解決問題是數學學習的核心”。數學教學不僅是為了讓學生學到數學知識，更重要的是把數學應用于現實生活，能夠主動從數學的角度分析并解決生活中的實際問題。

省課題《基于問題解決能力提升的小學數學分析策略研究》側重于對學生解決問題分析策略的指導，使學生掌握必要的方法和策略，從而提升學生問題解決的能力。

1.“畫圖法”分析策略

畫圖是解決問題策略中最基本、最重要的分析策略。它不是把現成的圖畫好呈現給學生看，也不是直接告知怎樣畫，而是讓學生在思考的過程中產生畫圖的需要，在自己畫圖的過程中體會方法，感悟策略，發展思維，獲得思想。因此，畫圖是幫助學生解決問題最有效、最常用的方法。

例如：一年級常見的問題，小朋友們站一隊，從左數聰聰站在第8個，從右數聰聰站在第7個，這一隊一共有多少人？

對于剛接觸解決問題的學生來說，他們往往僅憑感覺會把兩個數直接相加，8+7=15（人），這樣聰聰就被誤算了兩次。教學中我們可以提醒學生用畫圖的方法來思考。

如果用“△”代表聰聰，用“○”代表其他小朋友。畫圖為：

○○○○○○○△○○○○○○

從圖中，學生可以很清楚地看出聰聰從左、從右共數了2次，正確列式為：8+7-1=14（人）；同時學生也發現了另一種方法：聰聰左邊的人數+聰聰+聰聰右邊的人數=總人數，即7+1+6=14（人）

鼓勵學生運用畫圖的方法分析和解決問題，讓一些看似復雜的問題，通過畫圖變得清晰、直觀，從而幫助學生分析數量關系，理清思路，促進學生問題解決能力的成長。

2.“假設法”分析策略

假設法是根據問題的已知條件，先做一個假設，然后根據題意和假設之間的矛盾進行分析、調整，尋求解題途徑。它是解決“雞兔同籠”、行程、工程、推理等問題最基本的方法，有利于培養學生的邏輯思維能力。

例如：學校舉行知識競賽，每答對一題得10分，答錯一題扣6分，一號選手共搶答8道題，最后得分64分，他答對多少道題？

根據題意，答對一題得10分，答錯一題不僅得不到10分，還要扣去6分，即失去10+6=16分。現在假設一號選手8道題都答對了，他應得10×8=80（分），而實際上他只得了64分，失去80-64=16（分）。16÷16=1（題），由此可知，一號選手答錯了1道題，答對了7道題。

假設法是一種常用的推測性數學方法，其策略的呈現形式是多樣化的。我們應注重引導學生大膽假設，小心求證，把復雜的問題簡單化，以達到解決問題的目的。

3.“枚舉法”分析策略

枚舉法是根據問題本身的性質，一一列舉出該問題所有可能的解并在逐一列舉的過程中，檢查每種可能的解是否正確。該方法在小學數學中應用非常廣泛，它能幫助學生整理和篩選有用信息，進行有序思考，從而使問題得到解決。因其逐個考察了所有可能性，所以得出的結論是可靠的。

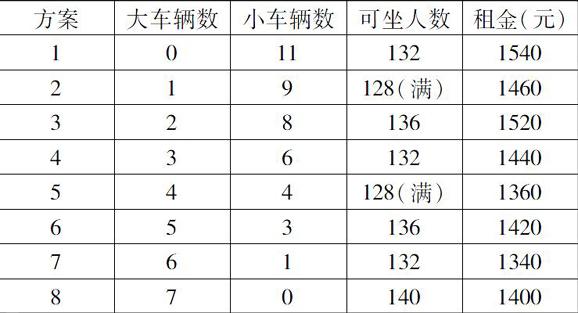
例如：128人外出考察，有兩種車可供租用。大車限坐20人，每輛車租金200元；小車限坐12人，每輛車租金140元。怎樣租車省錢？

學生一般會認為“坐滿沒有空位”是最優方案。列舉所有情況后發現方案7雖然有空位，卻是最便宜的。

列舉全部方案是有必要的，正好坐滿的方案，不一定是最優方案。枚舉法能夠引導學生全面、有序思考，不失為一種有效的解決問題策略。

4 “化繁為簡”分析策略

化繁為簡就是拋去繁雜的外衣，把問題簡化到最原始而又不失其本真的地方。將復雜問題簡單化是我們解決問題的一個重要策略。如人教版四年級下冊《雞兔同籠》就是運用了“化繁為簡”的思想。

原題為：“籠子里有若干只雞和兔。從上面數，有35個頭，從下面數有94只腳。雞和兔各有幾只？”由于數據較大，經過幾次簡單猜測和數據調整，學生仍然不能得到正確結果。為了便于研究，可以先從簡單的問題入手，把題中的35個頭和94只腳改為8個頭和26只腳。”

化繁為簡可以把復雜問題簡單化，學生研究起來更方便，更有利于發現規律，這樣可以有效地降低學習難度，提高學習效率。

5.“轉化”分析策略

“轉化”的分析策略是一種重要的解決問題方法，它把未學過的題目轉化成已學過的題目；把繁難的題目轉化成簡單的題目；把抽象的題目轉化為具體的題目，教學中需要我們引導學生靈活運用轉化策略化生為熟，化繁為簡，化抽象為具體，提高學生問題解決的能力。

在探究圖形面積和體積計算公式的推導過程中，都是將所研究的圖形轉化為已學過的圖形。例如：把平行四邊形轉化成長方形，把三角形和梯形轉化成平行四邊形，把圓轉化成近似的長方形，把圓柱的體積轉化為近似的長方體的體積等，

這些都是運用了“轉化”的策略。

生活中也有很多需要用“轉化”策略解決的問題。比如用排水法測量不規則物體的體積，就是將不規則物體轉化為規則物體。以測量土豆體積為例：在量杯中倒入200毫升的水，然后將土豆完全浸沒在水中，測出水和土豆的總體積為450毫升，最后用總體積-水的體積=土豆的體積。

在解決實際問題時，要結合具體情境，有意識地培養學生“轉化”的分析策略，提高數學思維能力。

總之，在教學中要注重解決問題分析策略的指導，開闊學生的視野，形成多樣化的問題解決策略，不斷豐富解決問題的方法，使學生的數學思維更具邏輯性、靈活性，最終提升學生問題解決的能力。