條件矩約束下一階自回歸模型的參數經驗似然推斷

彭毳鑫，胡 敏，趙志文

（吉林師范大學a.大學外語部；b.數學學院，吉林 四平 136000）

0 引言

考慮如下的一階自回歸模型：

對于自回歸模型的統計推斷，一直是統計學家關心的熱點問題之一。常學將和劉維奇[1]討論了自回歸模型的模型識別及其參數的高階Yule-Walker估計；倪均援[2]討論了有AR殘差的自回歸模型的參數估計和定階問題；國春光等[3]提出一種求解擾動項序列自相關系數及估計自回歸模型參數的迭代方法；林正華和馮仁忠[4]基于約束規劃及計算數學理論，給出了自回歸模型參數精確最小二乘估計方法；姜禮平[5]討論了有噪聲情形下自回歸模型參數的估計問題以及模型定階問題；呂效國等[6]研究了基于時間序列觀測數據，如何選擇自回歸模型的必要條件；吳鑑洪和朱力行[7]給出了一些診斷檢驗工具，用于向量自回歸模型的擬合優度檢驗問題；Chen等[8]利用非參數方法——經驗似然方法估計自回歸模型參數。本文進一步利用經驗似然方法，討論由輔助信息條件下模型（1）的參數估計問題。

經驗似然方法是Owen[9，10]提出的一種非參數估計方法。經驗似然方法有很多優點，如置信區域由數據本身決定，經驗似然比統計量的極限分布為卡方分布，因此在構造未知參數的置信區域時無需進一步估計漸近方差等。經驗似然方法最初主要用于總體均值的參數估計。近些年，該方法也被用于時間序列模型的統計推斷問題，如Chan和Ling[11]討論了GARCH模型的經驗似然統計推斷問題；Chen和Gao[12]討論了時間序列回歸模型的適應經驗似然檢驗問題；Zhao和Wang[13，14]分別討論了具有解釋變量的自回歸模型和隨機系數自回歸模型參數的經驗似然統計推斷問題，構造了未知參數的經驗似然比統計量，同時證明了統計量的極限分布為卡方分布；Chen等[15]討論了門限自回歸模型的經驗似然統計推斷問題。

在實際中，基于樣本觀測數據 X0，X1，…，Xn，經常能夠獲得一些輔助信息，這些輔助信息的形式多種多樣，如總體的分布為對稱的或非負的，方差是均值的函數等等。如果在統計推斷中有效的利用這些輔助信息，能夠提高統計推斷的精確性。本文中假定輔助信息能夠表示成為如下的條件矩：

其中 t=1，2，…，β0∈Rd為未知參數，g(Xt，Xt-1;β0)∈Rr，且 r≥d 。 為了敘述方便，將 g(Xt，Xt-1;β0)簡記為 gt(β0)。條件矩約束（2）包含廣泛的輔助信息類，如果條件方差為某一已知常數，序列的二階條件矩等于某一常數等。本文利用經驗似然方法，給出模型（1）已知輔助信息（2）時，參數α的估計問題。

1 方法和主要結果

本文討論如何應用經驗似然方法估計模型（1）中的未知參數α。假定如下條件成立：

A1:|α|＜1，即模型為平穩遍歷的；

A2: 存在 β0使得 E(gt(β0))=0;

下面討論未知參數α的估計。

首先基于經驗似然方法，獲得數據驅動的權。具體地，基于輔助信息 E(gt(β0))=0，令：

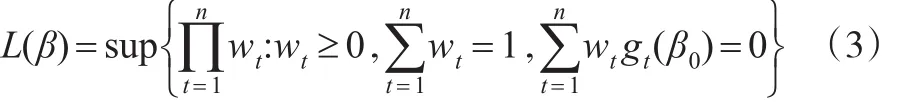
其中參數β0為待估的未知參數。由此可以獲得使L(β)達到最大的權w1，w2，…wn。基于該權函數，用如下的加權最小二乘方法估計未知參數α，即：

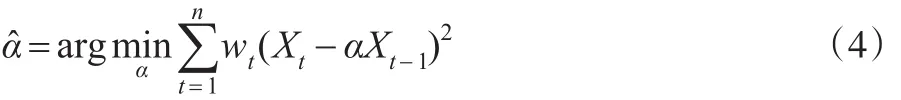
利用類似Owen[9]的方法，引入拉格朗日乘子λβ0∈Rr，經過簡單的代數運算可知：

其中λβ0滿足：

利用權（5），可以得到α的估計：

下面的定理給出了的極限分布。

定理1：假定條件A1-A2成立。如果α0是未知參數α的真值，那么：

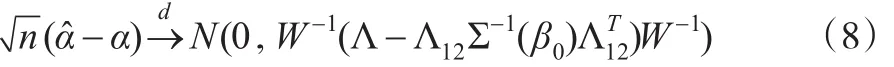
對于普通的最小二乘估計，其漸近方差為W-1ΛW-1。注意到Λ和Σ-1(β0)是正定的矩陣，因此與普通的最小二乘估計相比，本文所得到的估計的漸近方差減小。此結果進一步說明由于引入輔助信息，從而提高了估計的效。對于估計表達式（7），由于參數β0未知，因此，在實際中還無法使用該表達式估計未知參數α。為此，進一步使用最大經驗似然估計方法估計未知參數β0。具體地，令，利用Qin 和Lawless[16]的方法，進一步可知：

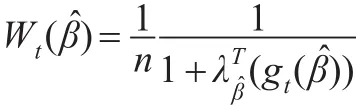
其中 (λβ，)滿足：

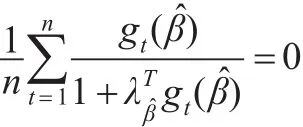
以及

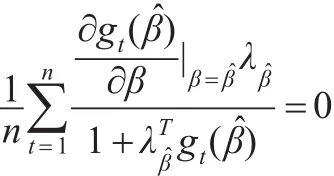
進一步令：

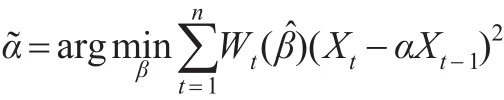
由此，可以用估計未知參數α。若r=d，即gt(β)的維數與β的維數相等，則，因此為普通的最小二乘估計。若r＞d，則加權最小二乘估計具有更小的漸近方差，因而與普通的最小二乘估計相比，加權最小二乘估計提高了估計的效。

下面的定理給出了估計量的極限性質。

定理2：若條件A1-A2成立，EX4t＜+∞，如果α0是未知參數α的真值，那么：

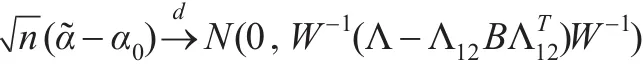
2 隨機模擬

下面通過隨機模擬來說明本文的方法的可行性。考慮如下的模型：

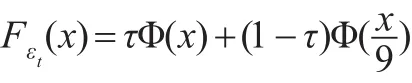
其中τ是固定的常數滿足0，＜τ＜1，Φ(x)是標準正態分布N(0，1)的分布函數。

計算具有輔助信息下加權條件最小二乘估計的均方誤差，即1000次估計誤差平方的平均值。樣本容量n=30， 50， 100。對于模型A，參數α分別取為-0.1，-0.2，-0.3，-0.4，-0.5，-0.6，-0.7，-0.8，-0.9，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，模擬結果由表1給出。對于模型B，參 數α分 別取為-0.1，-0.3，-0.5，-0.7，-0.9，0.1，0.3，0.5，0.7，0.9。τ分別取為0.8以及0.9表示不同的污染水平，模擬結果由表2給出。

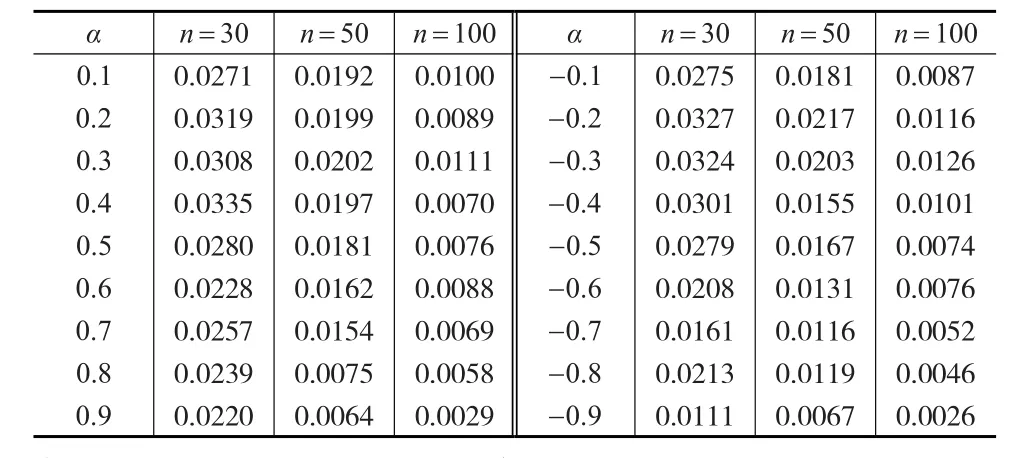
表1 模型A下參數估計的均方誤差

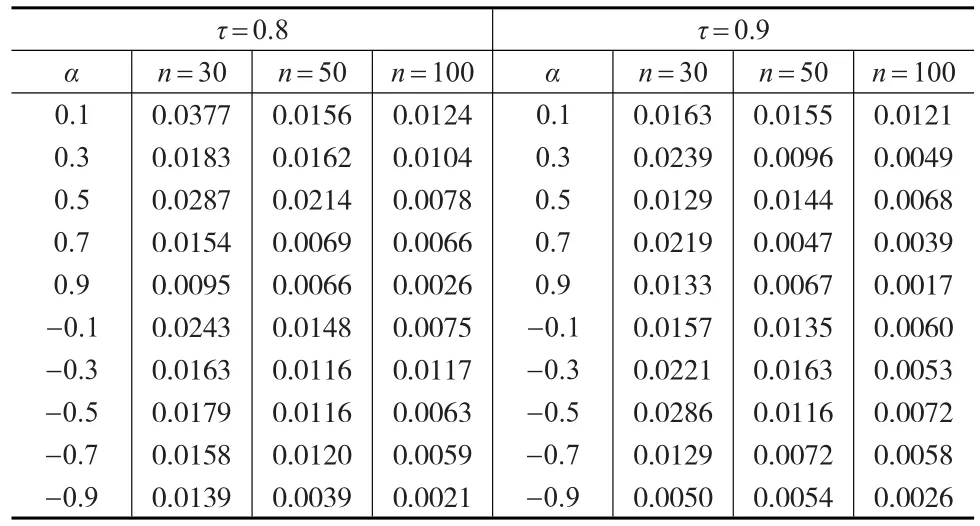
表2 模型B下參數估計的均方誤差

從表1和表2的模擬結果可以看出，對于不同的參數以及不同的樣本容量，本文的方法都具有較小的均方誤差，這也說明方法具有穩健性。

3 定理的證明

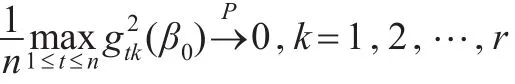
由條件A1可知：

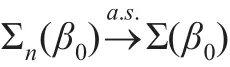
因此利用類似Peng等[17]引理1的方法證明，可以證明引理1成立。

引理2：假定A1-A2成立，EX41＜+∞，那么：

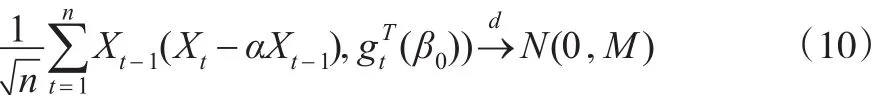
證明：由Cramer-Wold法則，只需證明對任意的非零向量C∈Rr+1，

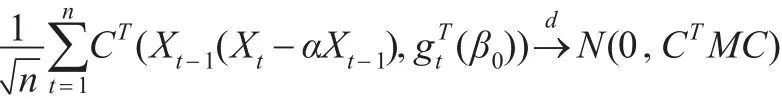
首先證明定理1，為此需要證明以下幾個引理。

引理1：假定條件A1-A2成立，那么：，因此：

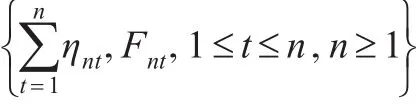
是零均值平方可積鞅陣，利用鞅的中心極限定理[18]只需證明：

以及

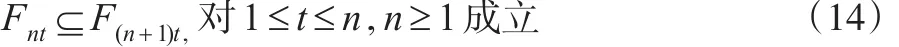
由σ代數的定義可知式（14）顯然成立。下面證明式（11），注意到對?ε＞0，

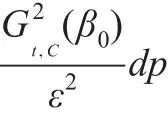
下面證明式（12）。由Lebesgue控制收斂定理可知：

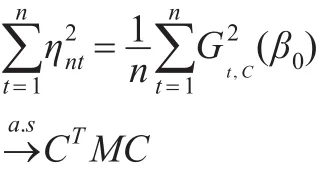
因此式（12）成立。

下面，證明（13）式。注意到：

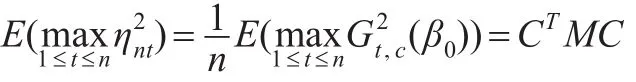
因此式（13）成立。綜上可知引理2成立。

引理3：假定A1-A2成立，EX41＜+∞，那么：

使用類似Owen[9]中的證明方法可以證明式（15）成立。

定理1的證明

由式（6）可知：

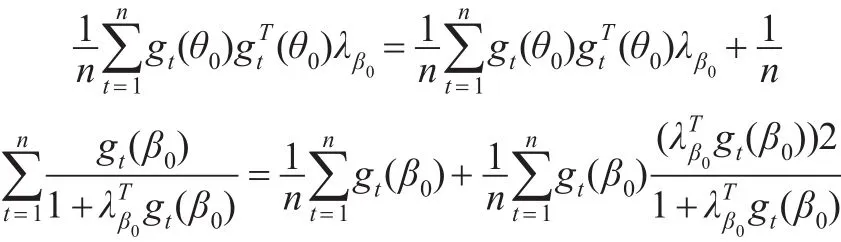
因此有：

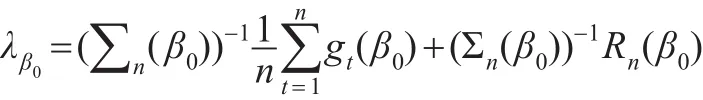
其中：

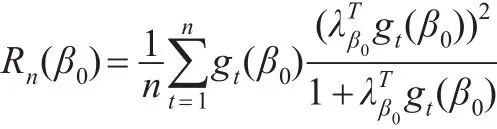
由引理1和2可知：

注意到對于?t，

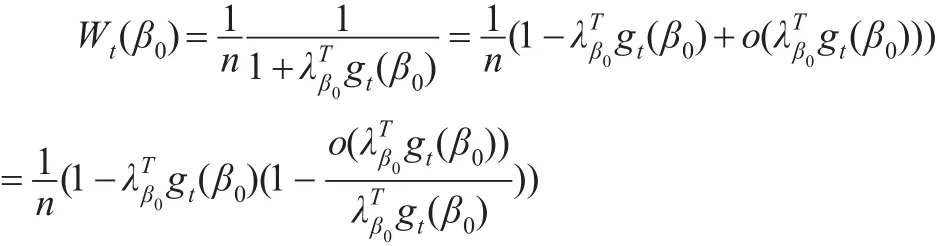
進一步由引理1和引理2可知：

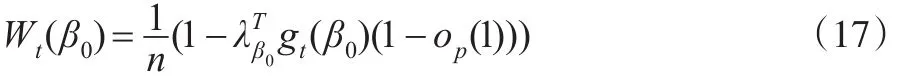
注意到：

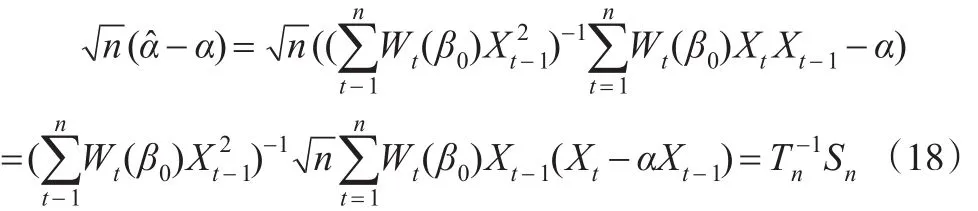
首先考慮Tn，由式（18）可知：

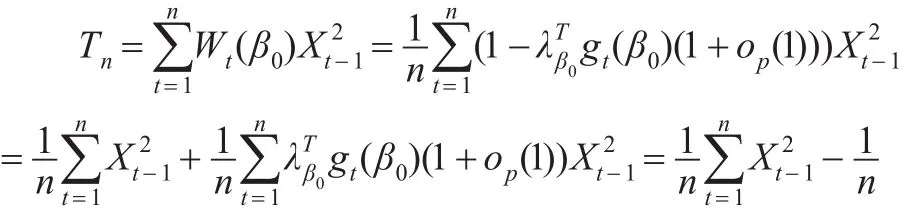
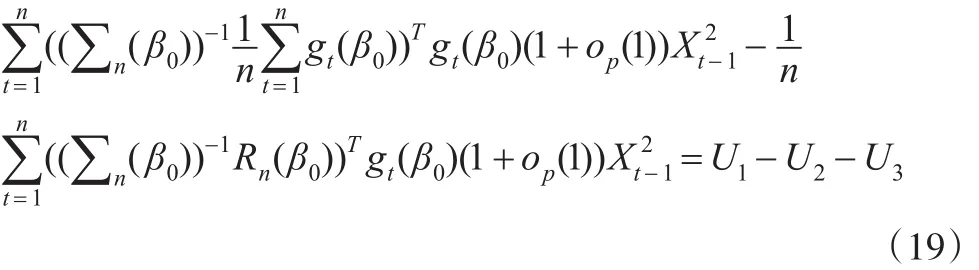
由條件A1和A2以及遍歷性定理可知：

同理可知：

綜合式（19）至式（21）可知：

下面考慮Sn，注意到：

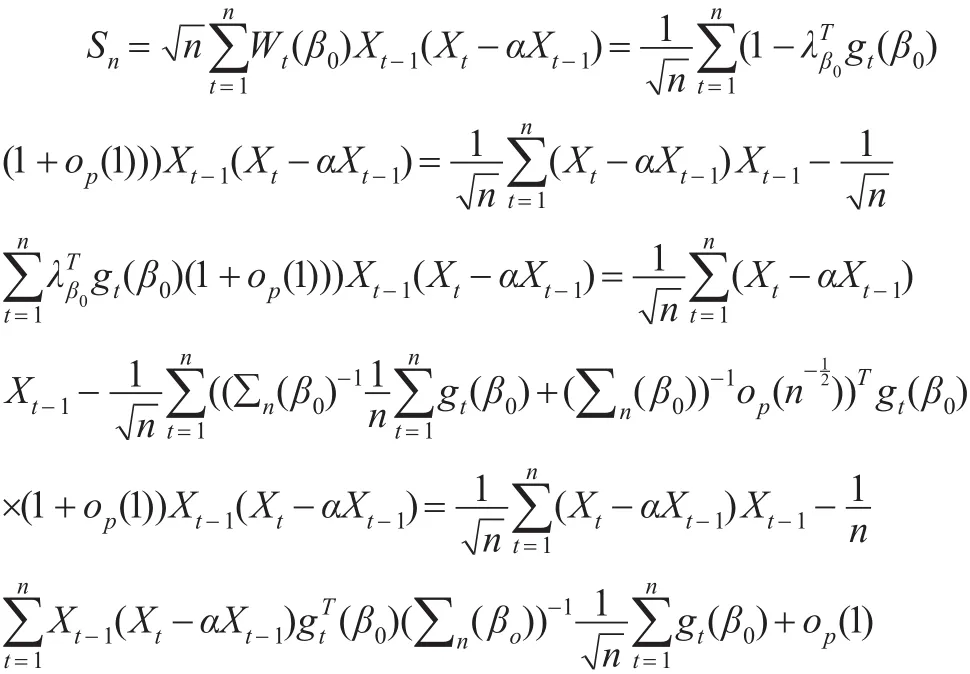
由遍歷性定理可知：

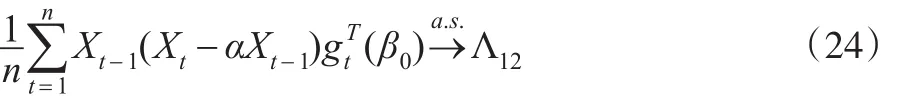
因此由式（10）以及式（24）可知：

由此證明了定理1。

類似定理1的證明，可以證明定理2。

4 結論

本文主要利用非參數方法——經驗似然方法討論了當輔助信息可以用條件矩約束表示時一階自回歸模型參數的估計問題。該方法與沒有利用輔助信息的模型參數的最小二乘估計相比較，具有更小的漸近方差。因此，有了更多的樣有本信息，得到的估計具有更高的效果。