一種新的基于群AHP和DEA的距離測度方法

范建平，朱兆鈺，吳美琴

（山西大學 經濟與管理學院，太原 030006）

0 引言

屬性權重的大小對于方案的評價結果具有很大程度的影響，是多準則決策問題中一個重要問題[1]。目前求解權重的方法可以主要分為主觀賦權法、客觀賦權法和組合賦權法。主觀賦權法是由決策者或專家根據自身的知識、經驗以及對決策問題的理解和判斷而直接給出偏好信息的方法，比如層次分析法（AHP）[2，3]、專家調查法（Delphi法）[4]、偏好比率法[5]等。客觀賦權法主要根據原始數據之間的關系由數據驅動來確定權重，比如主成分分析法[6]、熵值法[7]、數據包絡分析法[8，9]等。組合賦權法則是通過線性加權等方式將主客觀權重進行集結得出一個綜合權重的方法，該方法能夠給出更為合理的指標權重。其中諸多學者[10，11]通過將AHP方法和DEA方法相結合來獲得綜合權重，但是在這些研究中使用AHP方法來獲得主觀權重時僅考慮一位專家的判斷，這不利于對指標重要性的全面衡量。而在使用DEA方法確定客觀權重時通常采用原始CCR模型，該模型所求得的指標權重會存在權重不唯一的問題，這時通過該模型得出的客觀權重是最有利于評價單元自身的權重，使用該權重來進行評價并無法體現嚴格意義上的客觀性。

本文提出一種基于群AHP和DEA的閔式距離測度方法，該方法以閔式距離測度為中心模型，通過群AHP方法以及借鑒相對貼近度思想對多位專家的主觀判斷進行集結得到更為全面的主觀權重，通過能夠獲得公共權重的DEA方法來獲得客觀權重，從而確定各方案更為合理的綜合權重向量，進而計算得出各備選方案與理想方案之間的距離，根據計算得出的距離遠近來進行決策。這一方法綜合了群AHP、DEA和距離測度三種方法的優勢，使得該方法可以應用于更廣泛的評價、排序場合當中。最后通過一個國家可持續發展實驗區創新能力評價的實例來驗證該方法的有效性和可行性。

1 基于群AHP和DEA的綜合權重確定

1.1 基于群AHP的指標權重計算

群AHP是一種定性與定量分析相結合的多準則決策方法，其基本思想是把決策問題的有關元素按照支配關系形成層次結構，用一定標度對多位專家的主觀判斷進行客觀量化，構造出多個判斷矩陣，并在此基礎上計算各指標的權重系數，再將多位專家給出的權重系數進行集結得出最終的各指標權重系數。具體步驟如下：

（1）構造各位專家的判斷矩陣

判斷矩陣表示針對上一層次因素，本層次與之相關的因素之間相對重要性的比較。為了使決策判斷定量化，本文采用Saaty提出的1-9標度法。

（2）計算各位專家的指標權重值

計算判斷矩陣的最大特征值及其對應的特征向量，最大特征值所對應的最大特征向量即為各元素的權重。

（3）各位專家矩陣的一致性檢驗

①計算一致性指標CI

②查找相應的平均隨機一致性指標R.I.

對于1-9階判斷矩陣，該值可通過查表1得出。

表1 平均隨機一致性指標RI

③計算一致性比率C.R.

當CR＜0.1時，即認為判斷矩陣具有滿意的一致性，否則需要對判斷矩陣進行調整。

（4）各位專家的指標權重值集結

設邀請m位專家對具有n個指標的備選方案進行評估，將通過上述步驟得出的第i位專家評價的指標權重記為Wi=(wi1，wi2，...，win)(i=1，2，...，m)。在決策問題中，多位專家對決策問題進行決策時應遵循一致性最大化原則，因此對各位專家的重要性判斷則借鑒相對貼近度的思想，通過每位專家給出的指標權重之間的相對相似性程度來對專家的重要性進行判斷，而每位專家給出的指標權重之間的相似程度則通過歐氏距離來測量。

專家i與專家j通過AHP方法分別得出的指標權重分別為Wi=(wi1，wi2，...，win)，Wj=(wj1，wj2，...，wjn)(i≠j)，則 i和j兩位專家所給出的指標權重之間的相似度dij為：

在計算得出專家i給出的指標權重和其余m-1位專家所給出的指標權重之間的相似度后，選出專家i的指標權重與其余m-1位專家的指標權重之間最高和最低的相似度，分別記為，則專家i與其余專家的相對相似程度ci為：

通過將專家i給出的主觀權重的相對相似程度ci(i=1，2，...，m)進行歸一化，可得專家i的重要性程度vi為：

由此可得出各專家的權重值V=(v1，v2，...，vm)，則集結后的主觀指標權重為W1=(W1，W2，...Wm)×VT。

1.2 基于DEA的指標權重計算

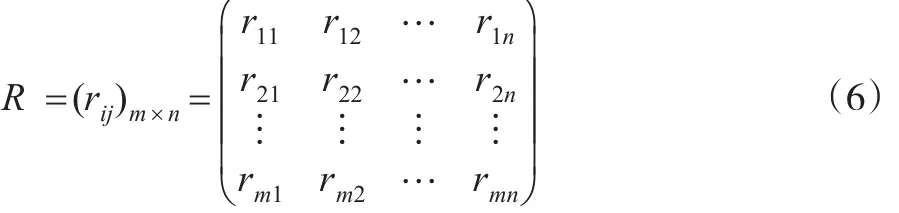
由于通過DEA方法求解得出的客觀權重與通過AHP方法求解得出的主觀權重相比可能會出現數值過小的情況，這會削弱客觀權重的作用，因此在運用DEA方法求解客觀權重之前首先需要將指標數據進行無量綱化處理。本文用式（6）將決策矩陣中的X=(xij)m×n無量綱化成相應的元素rij。

其中，對于效益型指標來說：

對于成本型指標來說：

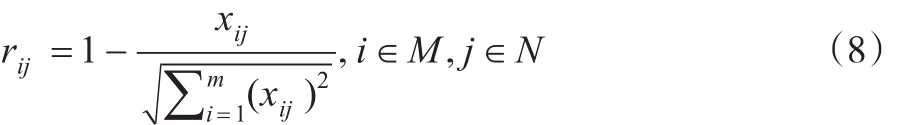
在對指標數據進行無量綱化后，接著運用DEA方法來求解客觀權重。運用DEA方法求解客觀權重所使用的是熊文濤等[12]所提出的基于理想決策單元確定公共權重的方法。假定有m個決策單元DMUi（i=1,2,…,m），n個評價指標，其中每個決策單元都有p種類型的輸入和q種類型的輸出，對應的輸入向量為Xi=(x1i，x2i，...，xsi，...，xpi)T，輸出向量為Yi=(y1i，y2i，...，yti，...，yqi)T，并且p+q=n，xsi＞0(s=1，2，...，p)，yti＞0(t=1，2，...，q)。同時，引入輸入權重向量V=(v1，v2，...，vs，...，vp)T，輸出權重向量U=(u1，u2，...，ut，...，uq)T。

1.2.1 效率下界的確定模型

通過公共權重，將所有DMUs的效率綜合在一起，得到下述的多目標分式規劃（MOFP）模型：

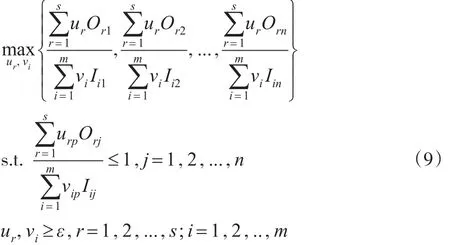
其中，ur，vi是所有DMUs的公共權重。

為了求解上述MOFP問題，引入非負變量α，將其作為每個DMU的效率下界，即，效率下界α越大越好。上述的多目標分式規劃可以進一步轉換為如下的非線性規劃模型：

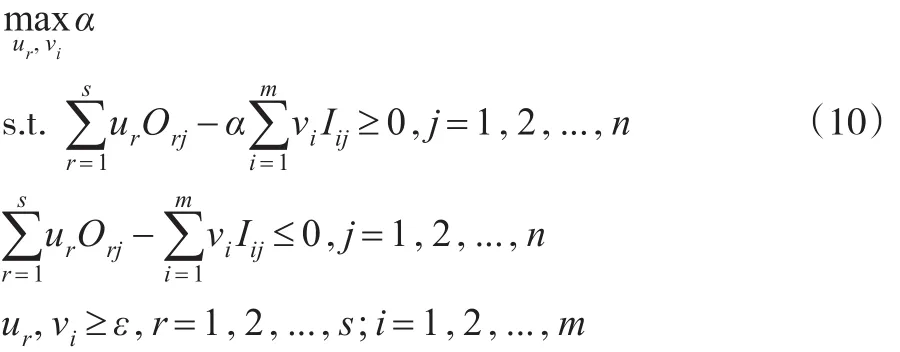
在模型（10）中 ，對于所 有DMUs來 說均會隨α的增加而不斷減少，當α增加到 某 個值α*時...，n將不會全部滿足，這時α*為模型（10）的全局最優解。為了計算α*，設，可構造如下的非線性規劃模型（11）：

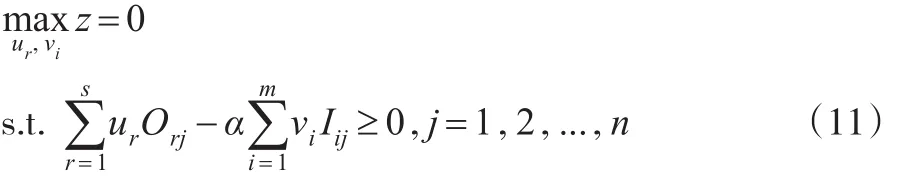
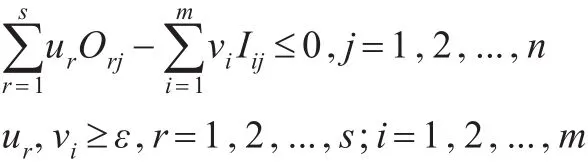
求解α*時采用二分法求解，具體步驟如下：

輸入：數據Iij，Orj，初始左端點a=0，右端點b=1，精度η。

輸出：所有DMUs的效率下界值α*。

第二步：令a=α*，若|b-a|≤η，則輸出α*；否則，轉第一步；

第三步：令b=α*，若|b-a|≤η，則令α*=a，輸出α*；否則轉第一步。

1.2.2 基于理想決策單元的公共權重的確定模型

當計算出所有DMUs的效率下界后，將α*帶入模型（11），得到一些線性約束條件。為了得到唯一的公共權重集，選取虛擬的理想決策單元作為參考對象來作為評價標準。假設有n個DMUs，每個DMUj（j=1，2，...，n）具有m個不同的投入Ij=(I1j，I2j，...，Imj)T，s個不同的產出Oj=(O1j，O2j，...，Osj)T。對于投入指標來說，選取所有DMUs中最小的數據作為理想決策單元（IDMU）相應的投入；對于產出指標來說，選取所有DMUs中最大的數據作為IDMU相應的產出。即

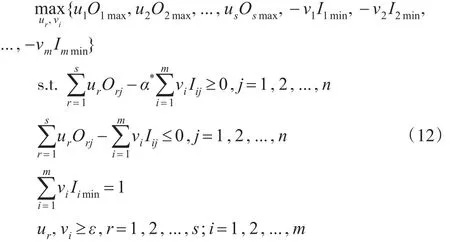
對于理想決策單元，總是希望以最小的投入得到最大的產出。可構建如下的多目標線性規劃模型：

其中α*為上文通過二分法得到的下界值。對于多目標規劃模型（12）采用分層序列法求解。求解得出的客觀權重為

1.3 綜合權重的計算

群AHP方法反映出多位評價者的主觀偏好，DEA方法反映了數據所包含的客觀信息，為了充分體現AHP方法和DEA方法的優點，本文將群AHP方法和DEA方法進行整合，采用線性加權的方法來共同確定評價指標的綜合權重。這種方法比單一的AHP方法或DEA方法更具有準確性和客觀性，具體計算公式如下：

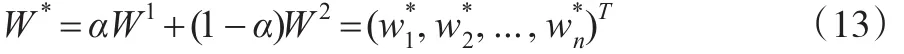
式中，W*為求得的綜合權重，α為主觀偏好系數，1-α為客觀偏好系數，α∈[0，1]。當面臨的決策問題或決策環境是基本確定的時，α的取值范圍為[0，0.5) ；當面臨的決策問題或決策環境存在風險時，α取值為0.5；當面臨的決策問題或決策環境具有高度不確定性時，α的取值范圍為(0.5，1]。

2 基于群AHP和DEA的閔式距離測度模型

距離測度是決策領域中一種有效的評價方法，在決策中使用距離測度的主要優勢是可以將備選方案與理想方案進行比較[13]，根據備選方案與理想方案之間的距離來最終確定最優方案，并且在評價過程中可以了解備選方案與最優方案之間各指標的差距，從而可以根據評價結果為決策者提出有效的對策和建議。在決策中使用的距離測度有不同的距離表達式形式[13，14]，比如海明距離、歐幾里德距離、閔可夫斯基距離。Merigó和Casanovas[14]指出閔可夫斯基距離是概括了包括海明距離、歐幾里德距離在內的一種距離測度，其通過使用誘導有序加權平均算子提出一個閔可夫斯基距離的一般形式。隨后，Casanovas等[15]將誘導閔可夫斯基有序加權平均距離算子應用到模糊環境中的再保險項目中。而Xian等[16]則將誘導有序加權閔可夫斯基距離算子擴展到模糊環境下，通過定義一個模糊語言變量距離提出了一個稱為模糊語言誘導有序加權閔可夫斯基距離算子的新算子，并且給出這一算子所具有的主要性質。但是在這些文獻中并未給出具體指標權重的獲取方法。

假定系統由m個方案和n個指標構成，則第i個方案的 n 個指標值構成數列Ai=(ai1，ai2，...，aij，...，ain)(i=1，2，...，m;j=1，2，...，n)，那么m個方案的原始指標值構成如下矩陣A：

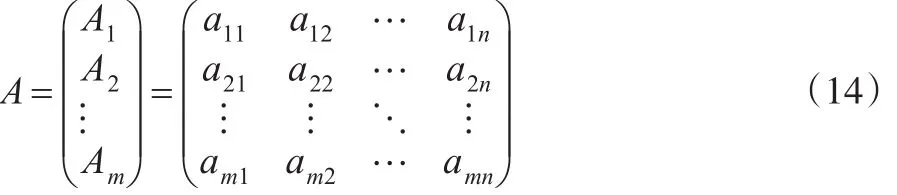
2.1 確定最優方案指標集

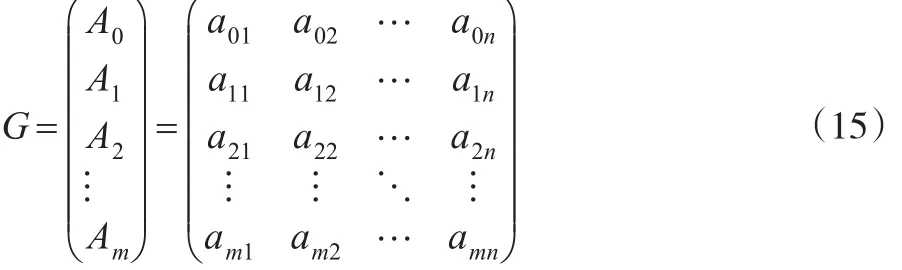
2.2 指標值的規范化處理

在上文運用DEA方法求解客觀權重時已經對數據進行過無量綱化處理，在這里則設按照式（3）、式（5）對數據處理后得到的規范化矩陣為H:

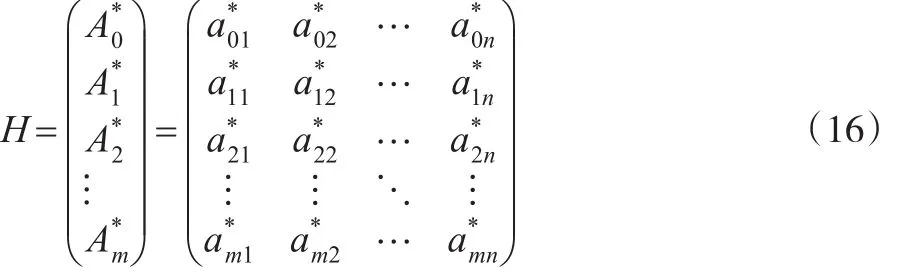
2.3 方案集與最優指標集的距離確定

根據指標權重向量W*，可求得各方案集與最優指標集的閔式距離[4]：

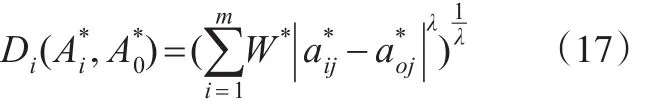
距離Di越小，說明方案集與最優指標集越接近，即方案集越優，因此可根據距離的大小來對方案進行優劣排序。

因此，本文提出的基于群AHP和DEA的多準則決策方法的步驟如下：

第一步：邀請多位專家通過對指標兩兩進行比較來對指標的重要性進行打分，通過群AHP方法以及借鑒相對貼近度的思想對多位專家所給出的主觀權重集結得出指標的主觀權重；

第二步：運用決策問題中的客觀數據，通過基于理想決策單元的DEA方法求解得出指標的客觀權重；

第三步：根據具體決策問題，遵循文中所給出的原則，確定主觀偏好系數α的值，進而將主客觀權重線性加權得出綜合權重；

第四步：通過加權閔式距離測度來對決策單元進行評價，并根據評價結果作出決策。

3 數值分析

3.1 指標體系

本文對中部六省八個城區型國家可持續發展實驗區創新能力進行評價，其評價指標體系見表2。

表2 國家可持續發展實驗區創新能力評價指標體系

3.2 基于群AHP的指標權重計算

邀請三位專家根據已確定的指標集，通過將指標兩兩進行比較得出判斷矩陣，經計算得出三位專家給出的指標權重分別為：W1=(0.2123，0.1131，0.0991，0.2330，0.1563，0.1036，0.0826)T，W2=(0.1203，0.1180，0.0369，0.2187，0.0508，0.1932，0.2620)T，W3=(0.1523，0.0499，0.1857，0.0265，0.0560，0.2898，0.2380)T。三位專家的權重為：V=(0.3148，0.3562，0.3290)，將三位專家得出的指標權重進行集結，得到AHP的 綜 合 權 重 為 ：W1=(0.1598，0.0941，0.1054，0.1600，0.0857，0.1968，0.1976)T

3.3 基于DEA的指標權重計算

將取值越小越好的成本型指標作為輸入指標，將取值越大越好的效益型指標作為輸出指標。在建模之前首先對指標的原始數據進行無量綱化處理，通過式（6），將每個實驗區的原始指標值無量綱化見表3。

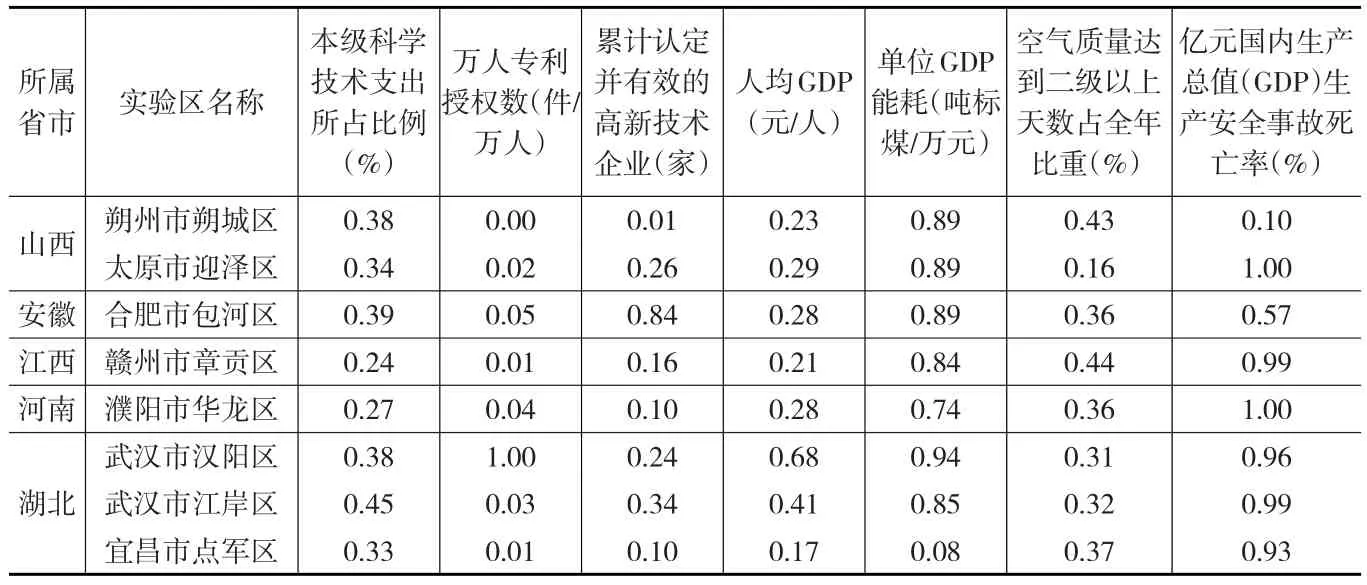
表3 中部六省城區型國家可持續發展實驗區創新能力規范化評價矩陣

本文運用Matlab編程軟件可求得客觀權重為：W2=(0.0781，0.0523，0.1461，0.1788，0.1895，0.1334，0.2218)T

3.4 綜合權重的計算

由于該評價環境較為確定，因此本文取主觀偏好系數α=0.2，根據上文給出的計算公式可得綜合權重為：W*=(0.0944,0.0607,0.1380,0.1750,0.1687,0.1461,0.2170)T3.5 基于群AHP和DEA的閔式距離測度模型

本文選取λ=1，根據式（17）可得各評價方案與最優指標集的距離Di(i=1，2，…，m)，根據距離Di的大小可對各實驗區的創新能力進行排名，即距離Di越小則該實驗區創新能力越高，具體結果見表4。

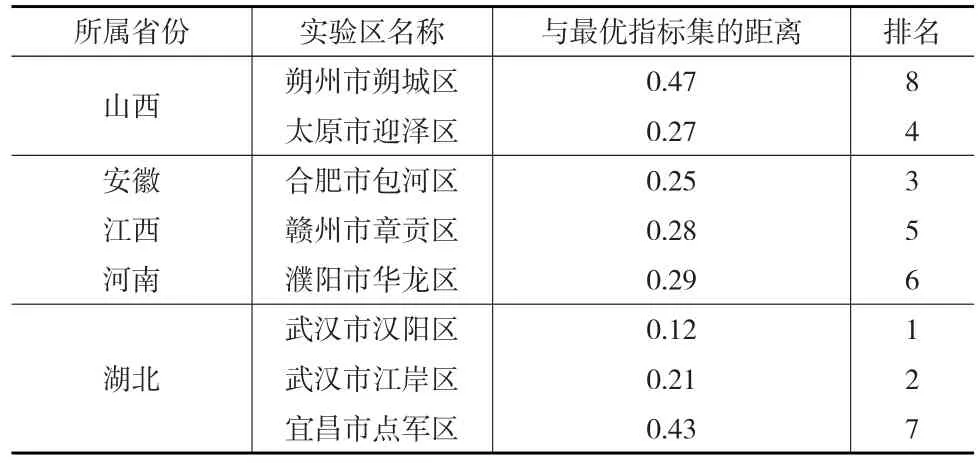
表4 中部六省城區型國家可持續發展實驗區創新能力的距離及排名

根據文中方法得出的中部六省城區型國家可持續發展實驗區的創新能力排名基本符合現實情況,由此證明了文中所提方法的有效性和可行性。

4 結束語

本文提出了一種新的基于群體AHP和公共權重DEA相結合的獲取綜合權重的閔式距離測度模型，通過使用群AHP方法以及借鑒相對貼近度的思想將多位專家給出的指標主觀權重進行集結得出更為全面的主觀權重，使用能夠得出公共權重的DEA方法來確定更為客觀和公平的客觀權重，從而共同確定更為合理的評價指標的綜合權重向量，其既能夠反應多位專家的主觀判斷偏好同時也綜合考慮了數據中所反映的客觀情況，從而能夠避免單獨使用AHP方法的過于依賴專家的主觀判斷而造成的人為因素偏差以及單獨使用DEA方法的運用數據驅動而造成的無法反映決策者主觀偏好的問題。接著通過計算評價方案與最優方案之間的加權閔式距離來對方案進行排序，使用閔式距離測度可以提高該評價模型的適用范圍，能夠更好的適用于多種決策問題。該方法能夠更好的兼顧權重獲取過程中的主客觀因素，從而能夠增加決策過程的公平性和決策結果的可接受性。最后使用一個中部六省城區型國家可持續發展實驗區的創新能力評價實例證明了該方法的有效性和可行性。本文所提方法能夠對實驗區創新能力評價提供一定的參考，并且該方法也可以應用于更廣泛的評價、排序場合當中。