灰色面板數(shù)據(jù)的關(guān)聯(lián)決策評(píng)價(jià)模型拓展

蔣詩泉，劉思峰，劉中俠，謝乃明

（1.銅陵學(xué)院 數(shù)學(xué)與計(jì)算機(jī)學(xué)院，安徽 銅陵 244000；2.南京航空航天大學(xué) 經(jīng)濟(jì)與管理學(xué)院，南京 210016）

0 引言

灰色關(guān)聯(lián)分析是一種因素分析方法，且對樣本量的多少和有無規(guī)律都能夠適應(yīng)，其基本思想是根據(jù)序列曲線幾何形狀的相似程度來判斷不同序列之間的聯(lián)系是否緊密[1]。國內(nèi)外學(xué)者在關(guān)聯(lián)度模型方面研究成果豐富，比如：B型、C 型關(guān)聯(lián)度[2，3]、T型關(guān)聯(lián)度、斜率關(guān)聯(lián)度[4]、凸關(guān)聯(lián)度[5]、面積關(guān)聯(lián)度[6]、廣義關(guān)聯(lián)度[7]、相似性和接近性灰色關(guān)聯(lián)模型[8]、多維空間關(guān)系的關(guān)聯(lián)度模型[8,9]。文獻(xiàn)[10,11]將向量空間的關(guān)聯(lián)度模型拓展到矩陣空間，進(jìn)而提出了基于面板數(shù)據(jù)的灰色關(guān)聯(lián)度模型及其性質(zhì)。對于面板數(shù)據(jù)的關(guān)聯(lián)模型度研究很少，且多以凹凸性等視角進(jìn)行刻畫此關(guān)聯(lián)關(guān)系，但是這對較為分散的面板數(shù)據(jù)往往很難準(zhǔn)確刻畫整體發(fā)展趨勢[12]。對于面板數(shù)據(jù)類型為一般灰數(shù)的關(guān)聯(lián)模型研究極其稀少，文獻(xiàn)[13-15]僅研究了決策信息為區(qū)間灰數(shù)的一般關(guān)聯(lián)決策模型。在實(shí)際決策問題中，可能會(huì)造成決策信息表現(xiàn)為復(fù)雜性和不確定性，而目前對不確定信息表征和運(yùn)算不夠完善。為更加準(zhǔn)確地表征不確定信息，本文首先給出了一般灰數(shù)的概念并用一般灰數(shù)表征復(fù)雜信息和不確定性、一般灰數(shù)的距離測度方法及其運(yùn)算法則；其次，將灰色面板數(shù)據(jù)轉(zhuǎn)化為時(shí)間關(guān)于樣本在指標(biāo)上值的時(shí)間矩陣序列；最后，基于關(guān)聯(lián)度構(gòu)造思想，構(gòu)建灰色面板數(shù)據(jù)的灰色關(guān)聯(lián)度模型并應(yīng)用于動(dòng)態(tài)多指標(biāo)綜合評(píng)價(jià)。

1 灰色面板數(shù)據(jù)關(guān)聯(lián)度模型的理論基礎(chǔ)

1.1 一般灰數(shù)的相關(guān)理論

定義1[1]：設(shè)，則稱g±為一般灰數(shù)。其中任一區(qū)間灰數(shù)，滿足且分別稱為g±的下界和上界，其中區(qū)間灰數(shù)和實(shí)數(shù)是一般灰數(shù)的特例。

定義2[1]：（1）設(shè)為一般灰數(shù)，稱為g±的核。（2）設(shè)g±為概率分布已知的一般灰數(shù)，的概率為pi且滿足pi＞0 ，，則稱為g±的核。

定義3[1]：設(shè)一般灰數(shù)的背景或論域?yàn)闉?Ω 的測度，則稱為一般灰數(shù)g±的灰度。一般灰數(shù)g±的灰度亦簡記為gο。其中，記為 ?i的灰度，且

定理1：設(shè)R(g±)為一般灰數(shù)構(gòu)成的集合，一般灰數(shù)g1±和g2±之間的距離滿足三個(gè)條件：

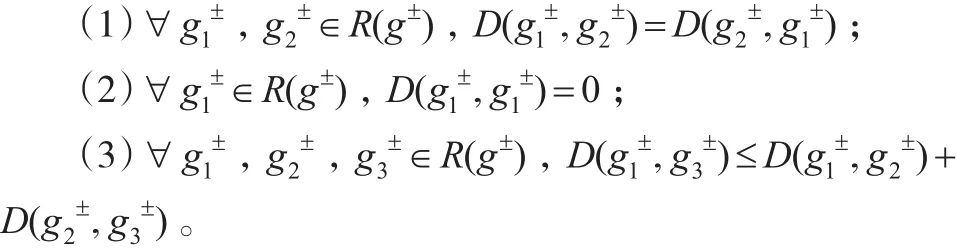
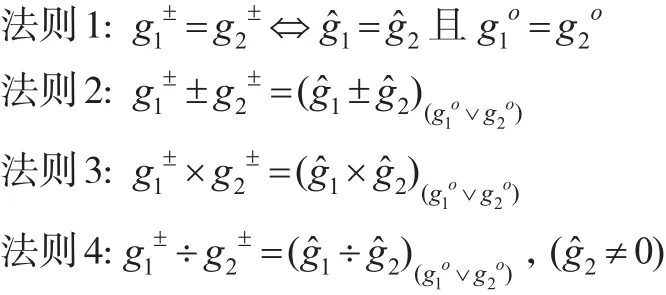
1.2 灰色面板數(shù)據(jù)的矩陣表示

灰色面板數(shù)據(jù)結(jié)構(gòu)比較復(fù)雜，它的橫向是截面數(shù)據(jù)，縱剖面是時(shí)間序列。設(shè)有N個(gè)樣本，每個(gè)樣本有M個(gè)指標(biāo)，觀測時(shí)間長度為T，那么可以將面板數(shù)據(jù)轉(zhuǎn)化為一個(gè)二級(jí)二維表的形式[13]，為了便于編程計(jì)算，將灰色面板數(shù)據(jù)用矩陣表示，具體見定義5。

定義5：設(shè)有N個(gè)樣本，每個(gè)樣本有M個(gè)指標(biāo)，觀測時(shí)間長度為T，灰色面板數(shù)據(jù)X(?)中第t時(shí)刻關(guān)于樣本i在指標(biāo)m的值記為gt±(i，m)＞0 ，其中i=1，2，…，N，m=1，2，…，M，t=1，2，…，T。則稱為t時(shí)刻的樣本指標(biāo)觀測矩陣。那么對應(yīng)的灰色面板矩陣序列X(?)=(X1(?)，X2(?)，…，XT(?))稱為時(shí)間矩陣序列。

類似于定義5可以定義樣本矩陣序列及指標(biāo)矩陣序列，由于這三個(gè)序列沒有主次之分，只是角度不同而已，且關(guān)聯(lián)度模型的構(gòu)造機(jī)理極其相似，故本文以時(shí)間矩陣序列為例研究灰色面板數(shù)據(jù)的關(guān)聯(lián)度模型。

2 灰色矩陣數(shù)據(jù)規(guī)范化算子

在決策評(píng)價(jià)過程中為了消除指標(biāo)量綱和量級(jí)的影響以及使其具有可比性，首先要對指標(biāo)進(jìn)行規(guī)范化處理。設(shè)第t個(gè)時(shí)刻關(guān)于樣本i在指標(biāo)m的值記為，其中t=1，2，…，T。

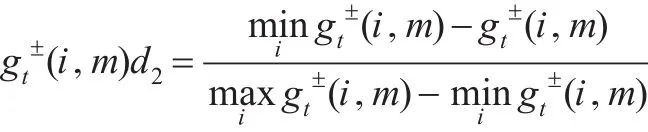
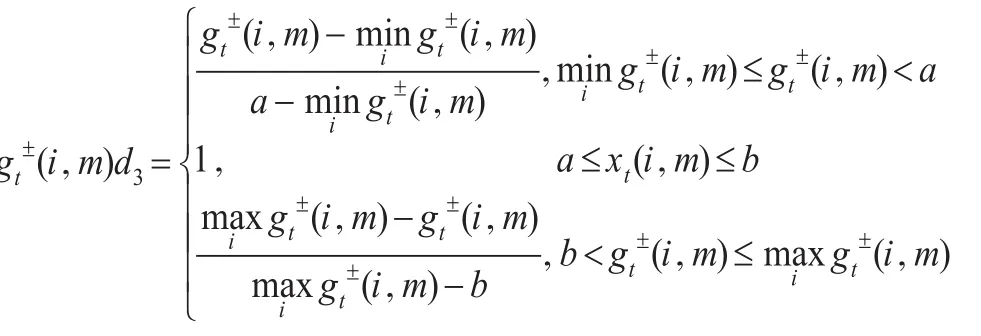
3 灰色面板數(shù)據(jù)的關(guān)聯(lián)度模型構(gòu)建

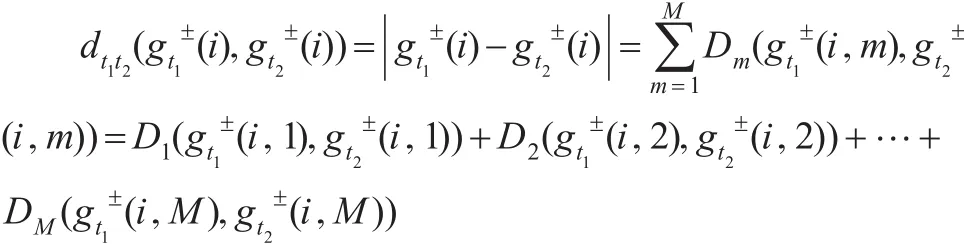
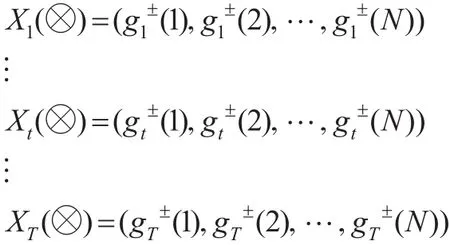
對于ξ∈(0，1)令：

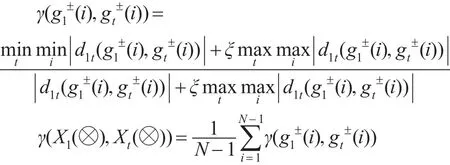
稱γ(X1(?)，Xt(?))為基于時(shí)間的灰色面板數(shù)據(jù)關(guān)聯(lián)度。

可以證明該關(guān)聯(lián)度滿足：

類似地，可以定義基于樣本的灰色面板數(shù)據(jù)關(guān)聯(lián)度模型、基于指標(biāo)的灰色面板數(shù)據(jù)關(guān)聯(lián)度模型。

4 基于灰色面板數(shù)據(jù)的關(guān)聯(lián)度決策算法步驟

步驟1:灰色面板數(shù)據(jù)規(guī)范化預(yù)處理。

步驟2:確定正、負(fù)理想樣本矩陣。

gt±(i，m)為第t個(gè)時(shí)刻關(guān)于樣本i在指標(biāo)m的值規(guī)范化后記為rkji，則t時(shí)刻正、負(fù)理想為:

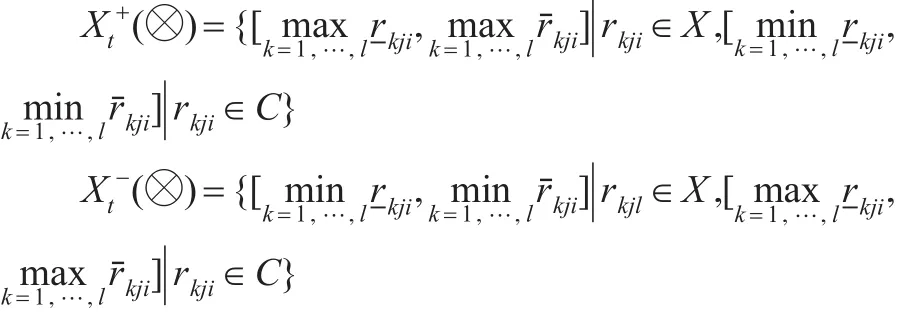
其中X,C分別表示效益型指標(biāo)和成本性指標(biāo)。

步驟3：將規(guī)范化決策評(píng)價(jià)矩陣表示為簡化形式的灰色決策矩陣。

步驟4：分別計(jì)算與正、負(fù)理想矩陣的關(guān)聯(lián)度值。

步驟5：計(jì)算相對貼近度并進(jìn)行排序。

5 案例分析

設(shè)有三家企業(yè)A1，A2，A3，評(píng)價(jià)指標(biāo)為S1：表示企業(yè)年產(chǎn)值（千萬元），S2:表示企業(yè)社會(huì)效益（千萬元），S3：表示對環(huán)境效率，三個(gè)時(shí)間樣本點(diǎn)分別為2012—2014年。考慮篇幅限制，將灰色面板數(shù)據(jù)轉(zhuǎn)化為三個(gè)時(shí)間序列決策矩陣如下，對三家企業(yè)進(jìn)行綜合評(píng)價(jià)。

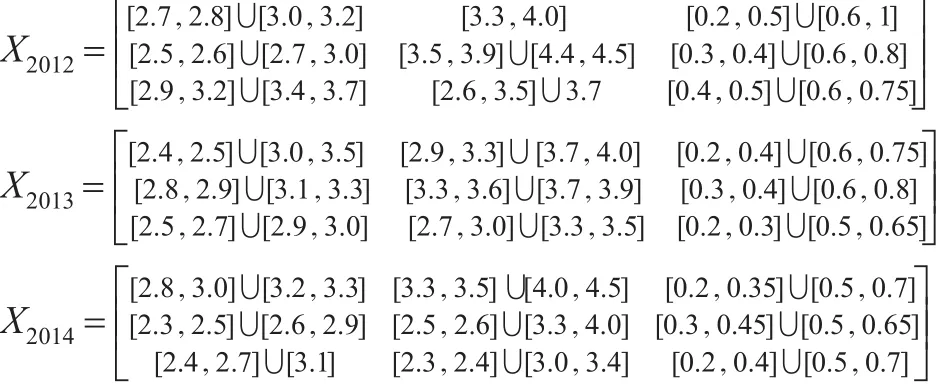
步驟1:將決策矩陣進(jìn)行規(guī)范化處理。

步驟2:確定正、負(fù)理想樣本時(shí)間矩陣。

步驟3:將規(guī)范化矩陣表示為簡化形式的矩陣。

步驟4：計(jì)算正理想方案與各樣本的關(guān)聯(lián)度。分別計(jì)算正理想與各樣本之間的距離d+i(m)、關(guān)聯(lián)系數(shù)和關(guān)聯(lián)度γ+i。

類似可以計(jì)算，d+2(1)=1.206，d+2(2)=0.605，d+2(3)=0.9945。d+3(1)=1.003，d+3(2)=0.998，d+3(3)=1.31。

根據(jù)定理2計(jì)算正理想與各樣本的關(guān)聯(lián)系數(shù)分別為：

正理想與樣本的關(guān)聯(lián)度值分別為：γ+1=0.809，γ+2=0.814 ，γ+3=0.721。

故關(guān)聯(lián)度排序?yàn)椋害?2＞γ+1＞γ+3。也即樣本排序?yàn)锳2?A1?A3。

步驟5:計(jì)算與負(fù)理想的關(guān)聯(lián)度。分別計(jì)算負(fù)理想與樣本之間的距離d-i(m)、關(guān)聯(lián)系數(shù)γ-i(g-±(m)，gt±(m))和關(guān)聯(lián)度γ-i。計(jì)算方法類似以步驟4。

根據(jù)定理2計(jì)算負(fù)理想與樣本的關(guān)聯(lián)系數(shù)分別為：

負(fù)理想與各樣本的關(guān)聯(lián)度值分別為：γ-1=0.917，γ-2=0.863，γ-3=0.926。

故關(guān)聯(lián)度排序?yàn)椋害?3?γ-1?γ-2，也即樣本排序?yàn)锳2?A1?A3。

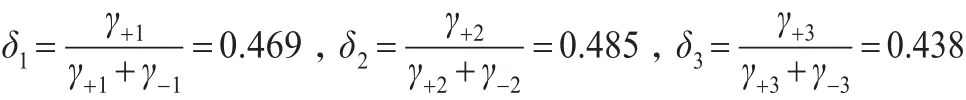
依照相對貼近度的方案排序?yàn)锳2?A1?A3。

通過以上的結(jié)論可以看出不論是依據(jù)與正理想的關(guān)聯(lián)度、與負(fù)理想的關(guān)聯(lián)度還是相對貼近度的排序其結(jié)果都是完全一致的。

6 結(jié)束語

為了克服區(qū)間灰數(shù)表征復(fù)雜不確定信息的缺失，本文利用一般灰數(shù)表征復(fù)雜不確定信息，解決了決策信息不能夠被充分精確表征的問題。本文基于灰色關(guān)聯(lián)度構(gòu)建的基本思想，將鄧式關(guān)聯(lián)度模型推廣到灰色面板數(shù)據(jù)的情形，在此基礎(chǔ)上構(gòu)建了基于灰色面板數(shù)據(jù)的多指標(biāo)動(dòng)態(tài)決策評(píng)價(jià)的關(guān)聯(lián)度方法，從而拓展了灰色關(guān)聯(lián)分析理論的應(yīng)用范圍，豐富了灰色關(guān)聯(lián)度理論。另外，在本文的基礎(chǔ)上，可以進(jìn)一步研究各指標(biāo)權(quán)重的確定方法、n維空間的決策模型構(gòu)建方法以及高維場數(shù)據(jù)的決策模型的構(gòu)建方法。最后的算例也充分驗(yàn)證了該模型的有效性和合理性。