廣義c-K估計優良性及其應用

錢 峰，張一枝

（1.常州工學院 數理與化工學院，江蘇 常州 213002；2.南通大學 理學院，江蘇 南通 226007）

0 引言

出現多重共線性問題時，統計人員會利用有偏估計克服最小二乘（LS）估計缺陷[1，2]。有偏估計的構造一般基于兩點考慮：其一，通過在樣本相關陣的主對角線上引進嶺參數以解決設計陣的病態問題，如嶺估計、廣義嶺估計[3，4]；其二，引進隨機壓縮系數將估計向原點壓縮以獲得較小的均方誤差（MSE），如Stein估計[5]。

本文將在PC準則下討論一種新的有偏估計壓縮廣義嶺估計相對于LS估計的優良性問題；給出各待定系數的確定方法，并通過實例驗證了該估計的可行性和優良性。

1 廣義c-K估計

考慮Gauss-Markov模型：

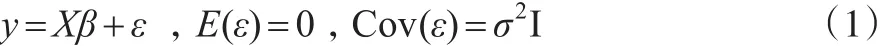
此處y是n×1維觀察向量，X是n×p維列滿秩矩陣(rank(X)=p)，ε是n×1維隨機誤差向量，β=(β1，β2，…，βp)′是p×1維未知參數向量。

對于p×p的正定矩陣X'X，必存在正交矩陣Q，使得：

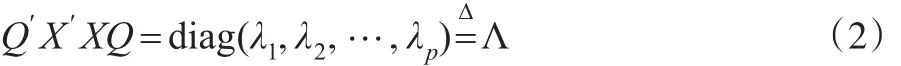
其中，λ1≥λ2≥...≥λp＞0為矩陣X'X的特征值。

對于模型（1），=(X′X)-1X'Y可作為未知參數β的LS估計。且有

設計矩陣矩陣X'X幾乎奇異或病態時，

定義1[2]：模型（1），β的嶺估計(ridge estimator)為：

其中k≥0為嶺參數。

定義2[3]：模型（1），β的廣義嶺估計(general ridge estimator)為：

其中K=diag(k1，k2，...，kp) (k1，k2，...，kp≥0) 稱為廣義嶺參數。

定義3[5]：模型（1），β的Stein估計(stein estimator)為：

其中，0≤c≤1為Stein壓縮系數。

近期，統計工作者提出了用一種新的有偏估計類廣義c-K估計，在考慮壓縮估計的同時通過解決設計陣存在共線性或近似共線性時的問題。

定義4[6，7]：模型（1），β的廣義c-K估計為：

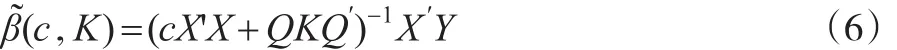
其中K=diag(k1，k2，...，kp)(k1，k2，...，kp≥0) 稱為廣義嶺參數，參數c≥1為壓縮因子。

易見，(c，K)是一個很大的估計類。特別地，c=1且K=kI(k≥0)時，得到β的嶺估計(k)；K=O（零矩陣）時，得到β的Stein估計c-1)；當c=1且有KQ=QK成立時，就得到β的廣義嶺估計

2 PC準則下廣義c-K估計估計的優良性研究

PC準則[8，9]作為比較不同估計量優劣的一個準則，原理為：設和為參數θ的兩個不同估計量為損失函數，若：

對一切θ∈Θ嚴格不等式“＞”至少對某θ∈Θ成立（Θ為參數空間），稱在PC準則下優于。

本文將討論對于損失函數：

在PC準則下，廣義c-K估計相對于LS估計的優良性問題。

為方便起見，記A=cX′X，G=QKQ′，Γ=A-1+G-1，則易知AG=GA，則A和G可同時對角化，事實上由上文和G=QKQ′知：

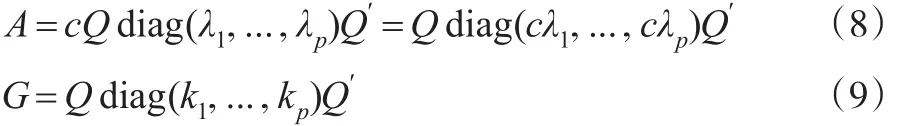
其中λ1≥λ2≥...≥λp≥0 是X'X的特征值，k1，k2，...，kp≥0是廣義嶺參數。

引理1：當c≥1時，cA1-A21是半正定矩陣，即

其中A1=(c-1)I+Γ-1A-1。

證明：設A1的特征值為μi(i=1，2，...，p)，下證c≥1時，對?i有μi2≤cμi成立。

事實上，利用公式（8）和公式（9），容易計算得：

則：

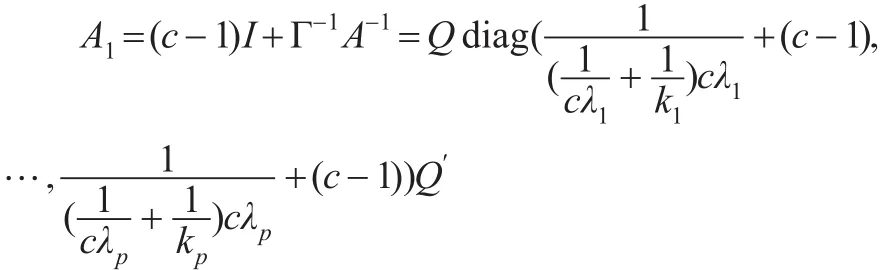
即：

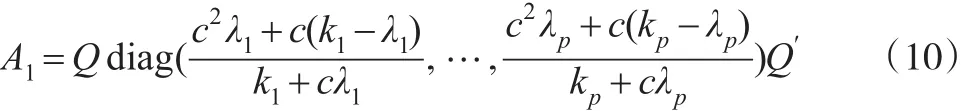
故A1的特征值分別為：

注意到：

又由于c≥1，故顯然成立，則(i=1，2，...，p),故引理成立。

另外，記：

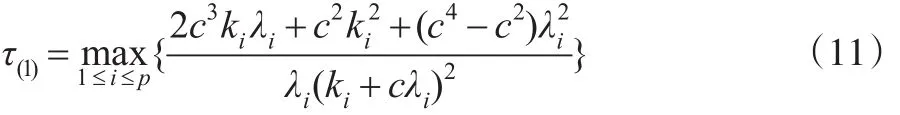
證明：

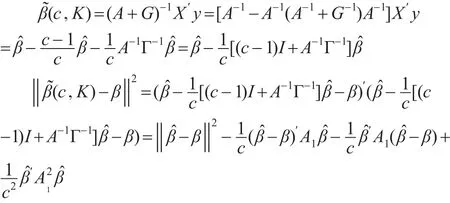
從而：

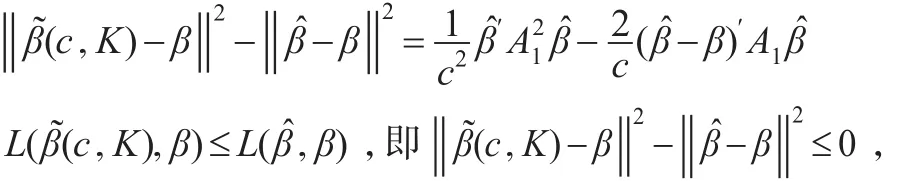
亦即等價于以下不等式成立：

而式（12）等價于下式：

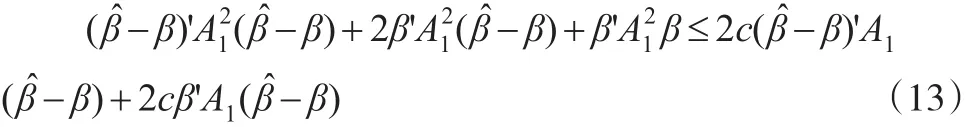
由引理知，A2

1≤cA1，故不等式（13）成立的充分條件為：

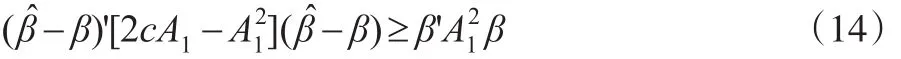
利用最小二乘估計的性質，易知-β的均值向量和協方差矩陣分別為：

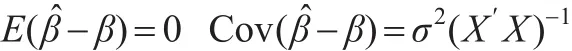
同時本文對于模型（1）作進一步假設：ε～N(0，σ2Ι)，故有：

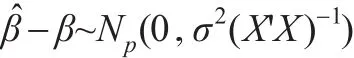
若記Z，則易知Z～N(0，Ip)。

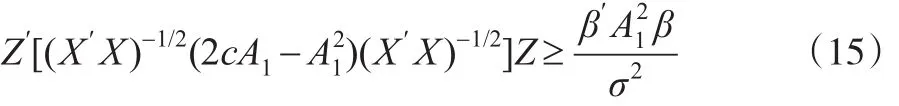
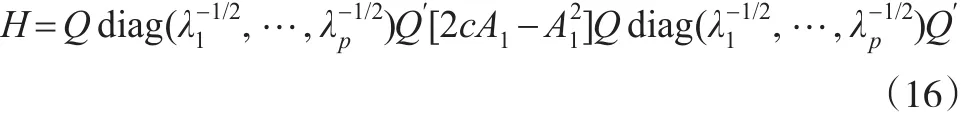
利用式（10）可求得H=Qdiag(τ1，τ2，…，τp)Q′，其中：

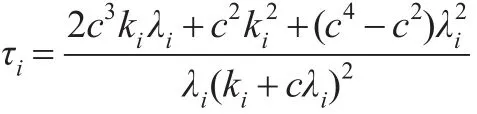
令B=Q′Z，則易知B～N(0，Ip)，故式（15）成立的充分必要條件為：

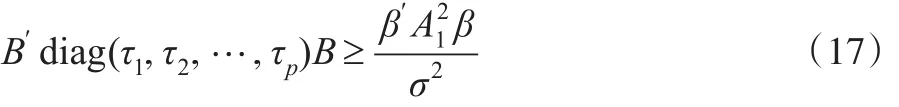
另由式（11）易知：

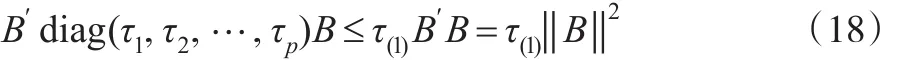
其中‖B‖2服從自由度為p的中心卡方分布。

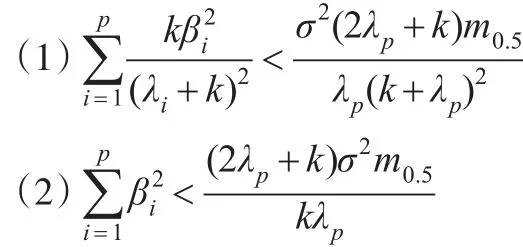
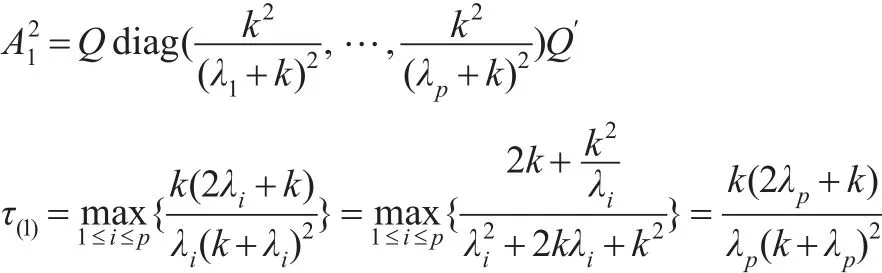
故：

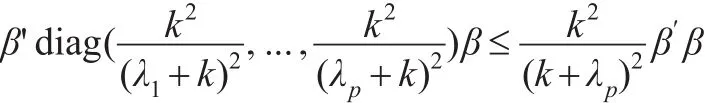
故上述推論得證。

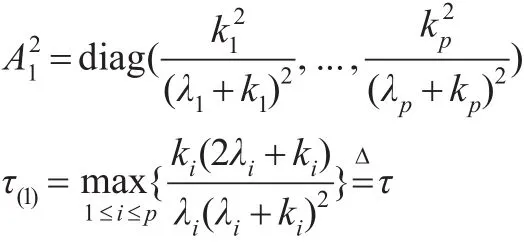
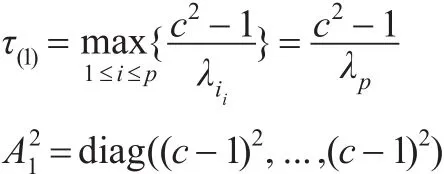
3 實例

3.1 廣義c-K估計參數c和K的確定準則

根據式（7）已經推導出有：

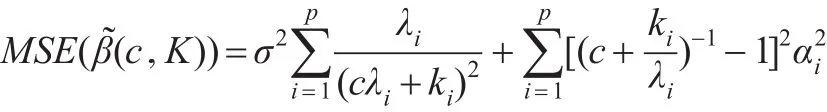
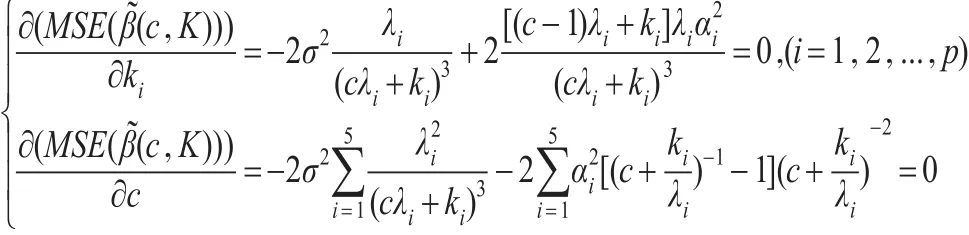
從中求的的駐點表達式為：

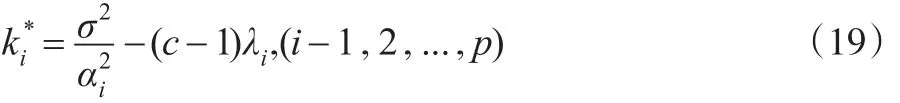
在實際問題中，由于上述表達式中σ的未知性，用數據的樣本方差來代替：

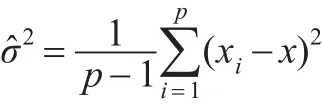
而真實值β也不易取得，故不妨用系數的最小二乘估計來代替。另外，在實際應用中未必一定要找出最優的k值,而是在均方誤差準則下找到優于約束最小二乘估計的盡可能小的k值即可。

3.2 實例分析

表1（見下頁）為1994—2003年共10年份的統計數據。其中Y表示民航客運量（萬人），X1表示國民收入（億元），X2表示消費額（億元），X3表示鐵路客運量，X4表示民航航線里程（萬公里），X5表示來華旅游入境人數（萬人）。（數據來源：《中國統計年鑒》）。

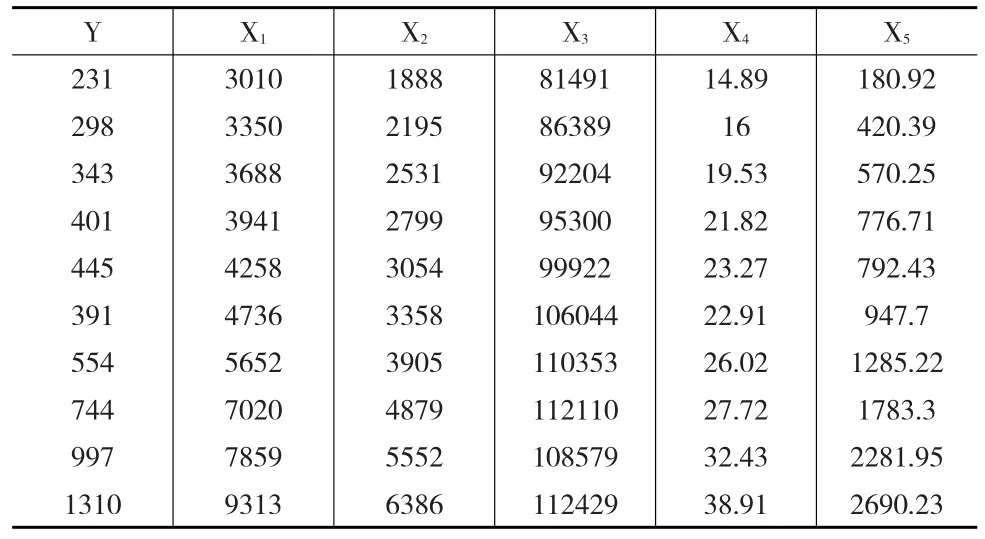
表1 中國民航客運量及相關數據

將數據中心化消除截距項后，利用最小二乘法，可得回歸模型：

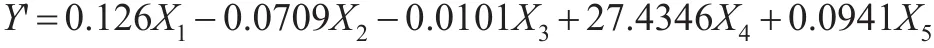
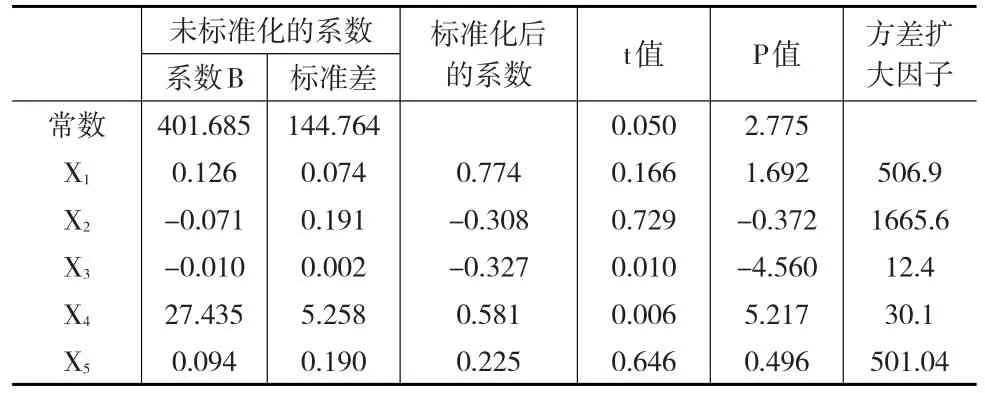
表2 回歸系數表

表2表明，X1，X3，X4這三個因素對民航客運量的影響是不顯著的，同時由表中的方差擴大因子都大于10，說明自變量之間存在著嚴重的多重共線性情況。因此，最小二乘估計不再是理想的估計。可以計算得到：

根據式（19）可以求得未知參數的表達式如下：

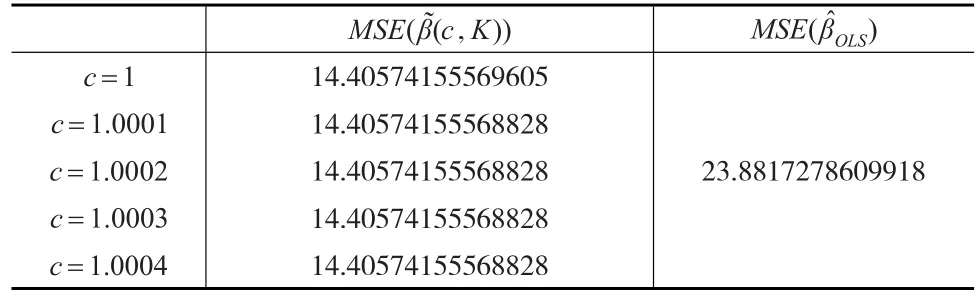
表3 兩種估計的MSE值比較

另外利用式（20），確定k1=1.3644，k2=47.826，k3=3.826，k4=1.6759，k5=12.345。

4 結論

作為廣義嶺估計的推廣估計，廣義c-K估計綜合體現了嶺估計、Stein估計的壓縮思想。通過理論證明和實例檢驗，均可看出其在Pitman Closeness準則、均方誤差準則下均有優于最小二乘估計的良好性質。這表明：在共線性場合出現時，該估計能較好地替代最小二乘估計。