含大規模屋頂光伏電站接入農村配電網多目標優化配置方法*

劉海濤，許倫，郝思鵬，張潮，高宇

(1.南京工程學院，南京 211167； 2.國網江蘇省電力有限公司江都區供電分公司，江蘇 揚州 225200)

0 引 言

伴著光伏發電技術不斷提高、成本持續降低，以及國家一系列促進光伏電站發展政策的出臺，加深了全社會對于光伏發電產業的認同感，使得用戶加入分布式光伏發電成為可能[1]。農村地區由于大量閑置的面積，建設屋頂光伏電站潛力巨大。考慮到未來的光伏能源的發展，城市地區安裝條件的限制，以及農村負荷對于供電質量的要求不斷提高等因素，進行農村配電網分布式屋頂光伏電站優化配置具有必要性。

在已有文獻中，針對小容量的屋頂光伏電站接入配電網選址定容分析還屬于空白，亟待填補。文獻[2-3]針對外部因素對屋頂光伏電站發電效率影響進行了分析，文獻[4]針對安陽市20 kW工程實際案例，綜合考慮光伏安裝地區的溫度、濕度、光照輻射、安裝傾斜角，分別分析了工程經濟效益、環境效益、社會效益。文獻[5]以小容量光伏電站的收益率、投資回收期、全壽命凈收益為指標，建立經濟性分析模型，并以用戶為中心進行分析驗證。文獻[6]通過PVsyst軟件模擬小容量光伏電站的發電量，結合上海地區實際用電類型、屋頂安裝方式以及補貼政策進行經濟性分析。

以上文獻都是以小容量光伏電站的經濟性指標為主結合其他因素進行分析，未考慮到大規模屋頂光伏電站接入配電網后對系統的影響。文獻[7]為簡化分布式發電選址定容分析模型，一階段采用經濟性指標結合權值系數得到選址結果，二階段應用粒子群算法以經濟成本為目標函數確定配置容量，這種方法雖然簡化了選址定容的計算復雜度，但選址和定容過程沒有同時進行，容易忽略最優解。文獻[8]考慮了分布式電源和負荷的時序特性，結合峰谷電價，以配電網網損費用最小為目標函數進行選址定容分析，這種方法可以精確反映配電網運行特征，使得選址定容結果更為合理，但是本文所研究的屋頂光伏電站單個容量遠遠低于傳統分布式電源容量，其時序性對配電網的影響較小，為簡化分析過程可以忽略。

基于以上分析，以IEEE-33節點配電系統為構架，以屋頂光伏電站建設投資成本最小化和系統網絡損耗最小化同時進行優化，綜合考慮農村地區安裝面積限制和配電網運行約束，構建了含大規模屋頂光伏電站接入農村配電網雙目標優化配置模型，并且應用針對高維度解改進的NSGA-II算法進行優化，最終通過模糊貼近度篩選出最優方案，并通過算例驗證該方案在滿足經濟性的同時對供電可靠性的影響。

1 屋頂光伏電站優化配置模型

1.1 屋頂光伏電站建設運行總成本

在文獻[9]的成本模型基礎上，考慮工程的收益周期，引入資金時間價值和設備殘值以及維護費用，更加準確地反映屋頂光伏電站建設運行投資的實際情況：

Call=C1+C2+C3

(1)

式中Call為屋頂光伏電站建設運行投資；C1為初始投資成本；C2為運行成本；C3為報廢時設備殘值。初始投資成本C1主要取決于配件成本和裝機容量，即:

C1=Csp·n+Cst+Civ+Cec+Cp

(2)

式中C1為光伏電站初始投資成本;Csp為太陽能電池板單位瓦數價格;n為屋頂光伏電站容量；Cst為支架總成本；Civ為逆變器價格；Cec為輸配設施價格；Cp為底座成本。

運行成本C2主要由設備維護成本構成，并且考慮資金時間價值，即：

(3)

Cma=C1K

(4)

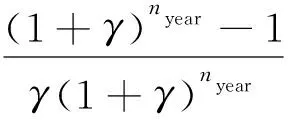
報廢時設備殘值C3主要由初始投資決定，即：

(5)

1.2 系統網絡損耗模型

在考慮農村配電網中屋頂光伏電站的接入位置以及容量時，以系統網絡損耗為衡量農村配電網電能質量的指標，有：

(6)

式中Ploss為配電系統網絡損耗；l為系統支路數；rk為系統k支路電阻；Ik為系統k支路通過的電流。

1.3 屋頂光伏電站布點模型

對于n個節點構成的配電網絡，采用0-1整數規劃配置模型的位置，用n維向量x=[x1,x2,…,xn]表示屋頂光伏的配置情況[10]。其中：

(7)

1.4 約束條件

(1)功率平衡約束

(8)

式中Pi、Qi為節點i向系統注入的有功功率、無功功率；n為系統的節點數；Ui、Uj為節點i、j電壓向量的幅值；Gij為節點導納矩陣元素Yij的實部；Bij為節點導納矩陣元素Yij的虛部；δij=δi-δj，為i、j兩節點電壓的相角差。

(2)電壓約束

UminUUmax

(9)

式中Umin和Umax為節點電壓允許的上下限，一般電壓正、負偏差的絕對值之和不超過額定值10%。

(3)屋頂光伏電站容量約束

設定屋頂光伏電站功率在15 kW以下，為了保證供電可靠性，接入節點的屋頂光伏有功功率不能超過節點負荷的30%，總的屋頂光伏有功功率不能超過總負荷的15%。

PiDG≤15 kW

(10)

PiDG≤30%PIL

(11)

(12)

式中PiDG為i節點接入屋頂光伏的有功功率；PiL為i節點負荷功率；m為接入屋頂光伏的節點個數。

2 NSGA-Ⅱ優化算法

2.1 NSGA-Ⅱ算法原理

帶精英策略的非支配排序算法(NSGA-II)采用快速非支配排序，對個體間的支配關系進行分層；采用虛擬適應度(dummy fitness)刪除過于集中的個體；引入精英策略，使父代和其產生的子代共同競爭產生下一代種群[12]。

應用NSGA-II算法對多目標函數進行優化主要包括4個步驟：

(1)快速非支配排序。賦予個體i兩個指標：其他個體支配個體i的數量ni；被個體i支配的其他個體的集合Si。排序過程中，把不被種群中其他個體支配的個體，即當前最優個體存入Frank，并賦予其非支配序rank，每次排序前，都需要將前次排序產生的Frank中的個體從種群中刪除；

(2)虛擬適應度計算。為了稀釋過于集中的個體，使得所有個體均勻地分布在Pareto前沿上，需要計算同非支配序rank下的所有個體之間的局部擁擠距離。

其計算步驟如下：

①對于邊界上的個體，其擁擠距離為無窮，即Pd(0)=Pd(End)=;

②對于排序在中間的個體i,其擁擠距離計算公式為：

(13)

式中Pd(i)為解i的擁擠距離；fk(i+1)為個體i+1的第k個分目標函數值；fk(i-1)為個體i-1的第k個分目標函數值；

(3)選擇運算。經過上述步驟，所有個體i都被賦予非支配序rank(i)和擁擠度Pd(i)。采用錦標賽的方式，從種群中隨機選擇個體，通過比較其非支配序rank和虛擬適應度Pd(i)，保留較好個體，淘汰較差的個體；

(4)精英保留。將父代Pt和通過父代交叉、變異產生的子代Qt合并成一個種群Rt。按照快速非支配排序對Rt進行分級，計算Rt中所有解的擁擠距離，按照非支配序rank進行排序，同一等級按照擁擠距離Pd排序，直至選取的個數達到外部檔案NS要求的數目，將選取的種群放入外部檔案NS，形成新一輪進化的父代種群Pt+1，通過下一輪的交叉、變異，形成新的子代Qt+1。

2.2 改進NSGA-II算法

NSGA-II算法在二維空間里，采用擁擠距離是可以表示個體的擁擠程度，但是在三維或更高維度的空間里，常規的擁擠距離并不能很好地表示個體的擁擠程度。故文獻[13]基于這一缺點，引入模擬退火算法中的Metropolis抽樣對同一等級下的解的排序進行修正。本文參考文獻[13]的方法，針對高維度NSGA-II算法進行改進，建立接受概率p。

(14)

式中Pd(j)為解j的擁擠距離；Pd(i)為解i的擁擠距離；T為溫度。

通過虛擬適應度篩選個體的過程中，每次個體間的篩選產生一個的介于0,1之間的隨機數ε，若ε小于概率p，則接受擁擠度較小的解，反之接受擁擠度較大的解。

采用Metropolis抽樣來修正虛擬適應度可以優化高維度空間中解的篩選，增強算法局部搜索能力。其實現流程如圖1所示。

3 模糊貼進度

多目標優化的結果是得到算法的非劣解集，最終的配置方案需要從集合中篩選出最優方案。采用模糊貼近度，通過比較各個配置方案與各單目標優化的理想配置方案的貼近距離，得到最優配置結果。

3.1 非劣解與理想解的模糊化

通過正態隸屬度函數對非劣解和理想解中各分目標值的接近程度進行量化，其公式為：

圖1 改進NSGA-II算法流程圖

(15)

式中k為非劣解個數;μ(frj)為第r組非劣解中的第j個目標函數隸屬度輸出結果；frj為第r組非劣解中的第j個目標函數值；fj*為理想解的第j個目標函數值。

其中，理想解是針對各個分目標函數進行單目標優化的結果。

將各個非劣解模糊化，以各分目標函數的隸屬度為變量的建立模糊向量Fr：

Fr=[μ(fr1),μ(fr2),…,μ(frq)]

(16)

式中由隸屬度含義得理想解的模糊向量為F*=[1,1,…,1]。

式中Fr為第r組非劣解的模糊向量；q是目標函數的個數；k為非劣解的個數。

3.2 模糊貼近度尋優

各非劣解模糊向量Fr和理想解模糊向量F*的貼近度可以表征兩個模糊向量的接近程度，采用式(17)計算：

(17)

式中σ(Fr，F*)為第r組非劣解的模糊向量Fr與理想解的模糊向量為F*的模糊貼近度。

σ(Fr，F*)值越大，表明Fr，F*越貼近；反之，則表明Fr，F*越遠離。

4 算例分析

以IEEE-33節點配電系統算例進行屋頂光伏的優化配置，如圖2所示。

圖2 IEEE-33節點配電系統

4.1 參數設置

在本文中，所有的屋頂光伏電站都簡化為恒功率輸出的PQ節點，且其功率因數恒為0.9。

屋頂光伏電進行規劃時，太陽能電池板單位功率價格為3 500 元/kW，支架總成本為3 500 元/戶，逆變器價格為10 000 元/戶，輸配設施價格為500元/戶，底座成本為3 000 元/戶，折現率為6.7%，周期年限為20年，維護比例K為10%，殘值比例為5%。

設置節點2～33為待安裝節點，選擇安裝屋頂光伏電站的數量為18個。

算法參數設置：種群規模pop=800，迭代次數Maxlt=400，外部檔案Ns規模Scalce=70，交叉幾率Pc=0.8，變異幾率Pm=0.1。

4.2 理想解優化結果

采用單目標遺傳算法對系統網絡損耗進行優化，求取此目標函數對應的理想解f*。結果如圖3所示。

圖3 系統網絡損耗優化結果

表1 單目標-網損優化配置方案

4.3 多目標優化結果

應用第2節針對高維度改進NSGA-II算法優化屋頂光伏電站配置結果的非劣解集在Pareto域分布如圖4所示。

圖4 Pareto前沿的分布情況

由分布情況可以看出，經過改進后的算法優化，非劣解均勻分布在整個Pareto前沿上，優化結果較好。并且隨著投資成本的增加，屋頂光伏電站總容量增大，系統網絡損耗不斷降低，符合實際情況。

4.4 模糊貼近度選擇

經上述改進NSGA-II算法優化后，NO.48-NO.52組非劣解見表2，可見各個解是半有序的，無法比較優劣。現用文中的模糊貼近度進行分析。

表2 Pareto解集中N0.44-48組非劣解

采用式(9)來計算各組非劣解對應的隸屬度，形成模糊向量結果見表3。

表3 N0.44-48組模糊向量

采用式(12)計算各組模糊向量與理想解的貼近度，結果見表4。

表4 N0.44-48組模糊貼近度

經改進NSGA-II算法優化后，產生了70組非劣解，按上述步驟對70組非劣解的模糊貼近度進行計算。結果為第46組非劣解最優。因此最優解為：

F46=[178 0432，175.882]

此種情況下對應的屋頂光伏配置見表5。

表5 最終配置方案

按此配置方案在IEEE-33節點系統中接入屋頂光伏，相對于未接入屋頂光伏電站的系統，在保證經濟性的同時，局部電壓水平得到改善，發揮了屋頂光伏電站對改善供電質量的作用，如圖5所示。

圖5 配置屋頂光伏電站對節點電壓的影響

5 結束語

針對大規模屋頂光伏電站接入農村配電網無序分布問題，首先建立了以系統網損最低和屋頂光伏電站建設運行總成本最低為目標函數的雙目標優化模型，應用針對高維度解的改進NSGA-II算法進行優化，最后應用模糊貼近度的思想針對非劣解集進行篩選，得到最終配置方案。優化結果表明，文中采用的針對高維度解的改進NSGA-II算法使得種群均勻分布在整個Pareto前沿上，提高了傳統NSGA-II算法的精度。優化得到的配置方案解決了屋頂光伏電站無序分布造成的分布式發電資源浪費的問題，在提高投資成本經濟性的基礎上，發揮了屋頂光伏電站作為分布式電源的作用，改善系統的局部電壓，提高系統的供電可靠性。