基于LLSE的配電網狀態估計器及優化方法
唐海國,劉海峰,朱吉然 ,張志丹,毛濤
(1. 國網湖南省電力公司電力科學研究院,長沙 410007; 2. 武漢東湖學院,武漢 430074)
0 引 言
國民經濟的快速發展帶動了電力需求的迅速增長,為了解決我國電能資源及負荷不協調的地理條件限制,近年來超高壓遠距離輸電進入了快速發展階段。由此也帶來了無功補償、絕緣保護、繼電保護和運行維護等方面的困難[1-4]。利用可再生能源發電給負荷就近供電,以此降低輸電損耗和提高供電安全性,是解決上述難題的一個新思路[5-6]。
分布式電源一般指安裝在負荷附近、利用新能源或可再生能源的小型發電裝置,如風電、光伏發電、生物質能發電等[7]。分布式電源的接入不僅不改變了原有的配網結構,便于安裝運行;而且有利于改善配網的供電可靠性和電能質量[8-9]。但由于分布式電源的輸出功率具有隨機性和波動性,給傳統的配電網狀態估計帶來困難。
傳統配電網狀態估計[10-11]是指對給定的系統結構及量測配置,在量測量具有誤差的情況下,估計出系統各母線上的電壓有效值和相角,及各支路潮流。由于考慮測量誤差的存在,其要求量測量具有冗余性,需要較多的測量裝置。本文設計了一種基于線性最小二乘法(Linear Least Square Estimate, LLSE)的實時電壓狀態估計器,在已知節點功率統計特性的情況下,僅少量電壓測量裝置,即可以較高精度估計全系統各節點電壓有效值和相角。
本文首先利用三相電壓降落計算建立配電網的電壓估計模型,根據線性最小二乘法得到估計器的表達式。分析風電等功率預測誤差較大電源接入配電網時對估計器性能的影響,建立了對監測裝置位置進行優化的模型,給出了其決策變量、目標函數和約束條件,通過在IEEE 33節點配電網絡中的仿真計算驗證了本文估計器設計和優化方法的正確性和有效性。
1 三相狀態估計器設計
1.1 區域電網節點電壓計算
設樹狀三相配電網絡節點集合為V={0, 1, 2,…,N},其中根節點為0號節點,且每個子節點比其父節點的編號大。設節點fi的子節點集合Cfi={i∈V|i>fi, (i,fi) ∈ε},其中ε為該配電網絡的邊集合。
忽略三相線路對地導納,節點i與其父節點fi的三相電壓關系為:
(1)

以a相為例,節點i與其父節點fi的電壓差為:
(2)
設三相電壓對稱,相角互差120°,忽略電壓降落橫分量,由式(2)得到a相電壓有效值之差為:


(3)

忽略配電網絡線路功率損耗,得到:
(4)

設式(3)右邊電壓有效值為1.0 p.u.,得到:

(5)
根據式(5),列寫除根節點以外的其他N個節點與其父節點的a相電壓有效值差表達式,寫成矩陣形式有:
(6)
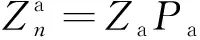
(7)

Pa∈N6N×6N的表達式為:
(8)
式中P∈NN×N是根據節點拓撲信息形成的矩陣,其表達式為:
(9)

S是功率矩陣,其形式為:
(10)
Pm∈NN×1和Qm∈NN×1是除根節點外的其余N個節點流出的m相有功和無功功率。
在包括根節點在內的M(M (11) 類似的,其余N-M+1個無測量裝置節點的電壓與根節點電壓有效值之差可表達為: (12) (13) 可使均方誤差最小。其中cov(·)是隨機變量的協方差,var(·)是隨機變量的方差。 (14) 同理,E(ΔVe)的表達式為: (15) 協方差cov(ΔVm,ΔVe)的表達式為: (16) (17) 將上述各變量的表達式代入式(13),得到: (18) 式(18)即為所設計的節點電壓有效值的狀態估計表達式,在已知每個節點功率的統計特性(均值和方差)時,根據電壓測量裝置提供的節點電壓有效值信息,可以對未放置電壓測量裝置節點的電壓有效值進行估計。 電壓測量裝置的位置不同,將對估計器精度產生很大影響,以電壓測量裝置位置作為決策變量, 可表示為: x=(x1,x2,…,xM) (19) 式中xi表示電壓測量裝置i所在的節點編號。 以a相電壓為例,對具有N+1個節點(其中根節點編號為0)的樹形配電網絡,在其中M個節點(包括根節點)放置電壓測量裝置,用平均均方根誤差(Average Root Mean Square Error, ARMSE)評價估計器的估計精度,ARMSE的表達式如下: (20) 以ARMSE作為目標函數,在給定電壓測量裝置數量時,當某一放置方案具有最小ARMSE時,認為此方案為最優放置位置。 在決策變量x中,不允許將兩個電壓測量裝置放在同一節點,即: xi≠xj,(i≠j) (21) 放置電壓測量裝置節點的數量需小于總節點數量,得到: M≤N (22) 綜上所述,狀態估計器的優化模型可以表示為: (23) 本文利用MATLAB以如圖1所示的IEEE 33節點配電系統為目標進行仿真計算,結果均以標幺值表示。 圖1 EEE 33節點配電系統 設0號節點電壓保持1.0 p.u.不變;對于一般的負荷節點,假設其流出有功功率和無功功率符合高斯分布N(μ,σ2),設σ=0.3μ;考慮分布式電源接入配電網絡,對于光電節點,也可認為其發電功率符合高斯分布N(μ,σ2);而對于風電節點,用威爾分布雙參數曲線[13]對風速進行統計描述,從而建立其發電功率的數學模型。 根據前推回代潮流計算[14]得到節點電壓有效值的真值,估計器得到的結果作為節點電壓有效值的估計值,以此計算ARMSE。 在給定的電壓測量裝置數量M的條件下,假設配電網絡中所有節點的功率都符合高斯分布N(μ,σ2),其中σ=0.3μ;利用粒子群算[15]法求解優化模型,得到最優放置位置,如表1所示(結果均以標幺值表示)。 表1 不同電壓測量裝置數量下的最優放置位置 可以看出,當電壓測量裝置增加到一定數量時,節點編號為17、24和31的節點出現的次數很頻繁,這是由于它們位于配電網絡一段饋線的末端,而饋線末端附近節點的誤差較大,需要放置電壓測量裝置以限制誤差。 在測量裝置放置在最優位置時,根據表1畫出估計器的ARMSE隨測量裝置數量的變化曲線,如圖2所示。 圖2 ARMSE隨電壓測量裝置數量變化曲線 可以看出,當電壓測量裝置的數量增加到7時,ARMSE的減小不明顯,而在電壓測量裝置數量小于6個時,ARMSE隨測量裝置數量增加明顯減小,故需找到一個合適的電壓測量裝置數量,以平衡估計器的高精度和經濟性。 如前所述,當風電節點接入配電網絡時,其發電功率特性不能用高斯分布來模擬。當測量裝置數量給定(5個)且放置在最優位置(0,2,7,15,31)時,在配電網絡的不同位置接入風電,用最大絕對誤差(Absolute Error, AE)和ARMSE兩個指標對估計器的性能進行評價。其中,最大絕對誤差定義為: (24) 假設風電節點只有一個,且裝設在節點編號為25-32的饋線段上,仿真結果如表2所示。 表2 風電節點接入下的ARMSE 可以看出,當配電網絡中接入風電時,估計器的精度略有下降;且當風電節點接在25-32號節點中部時,風電節點對估計器的精度影響較大,這是由于中部節點離安裝測量裝置的節點較遠,電壓測量裝置不能限制其誤差;因此,要限制風電接入配電網給估計器精度帶來的影響,需要在其附近安裝電壓測量裝置。 本文提出了一種基于線性最小二乘法的區域配電網三相狀態估計器,以解決電壓測量裝置數量有限和隨機性分布式電源接入時的配電網狀態估計問題。通過 IEEE 33節點配電網絡中的仿真計算結果表明,配電網絡線路末端附近節點的估計誤差較大,需配置電壓測量裝置以提高估計精度;估計器的估計誤差隨電壓測量裝置數量的增加呈指數形式下降,存在飽和現象;風電節點接入配電網絡時,估計器的估計精度下降,需在其附近安裝電壓測量裝置以限制估計誤差。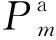


1.2 估計器表達式




2 狀態估計器的優化模型
2.1 決策變量
2.2 目標函數

2.3 約束條件
3 仿真及性能分析

3.1 電壓測量節點放置位置的優化


3.2 不同功率分布特性的優化

4 結束語

