logistic回歸概率模型在物質濃度辨識中的應用

王誠 劉碩

（蘭州石化職業技術學院信息處理與控制工程學院，甘肅 蘭州730060）

0 引言

比色法是目前常用的一種檢測物質濃度的方法，即把待測物質制備成溶液后滴在特定的白色試紙表面，等其充分反應以后獲得一張有顏色的試紙，再把該顏色試紙與一個標準比色卡進行對比，就可以確定待測物質的濃度檔位了。由于每個人對顏色的敏感差異和觀測誤差，使得這一方法在精度上受到很大影響。隨著照相技術和顏色分辨率的提高，希望建立顏色讀數和物質濃度的數學模型，即只要給模型輸入照片中的顏色讀數就能夠通過計算獲得待測物質的濃度，而模型的精度直接關系著待測物質濃度的準確性,見于監測數據呈現明顯的類狀或族狀，可以將物質濃度判斷問題歸結為類別辨誤問題或模式識別問題。為此，本文在已知顏色讀數和相應物質濃度實驗數據的基礎上建立了基于logistic回歸的物質濃度識別模型，該模型是實質上是一種多元非線性概率回歸分析模型，實例分析表明用該模型預測物質濃度具有很高的精確度，好于支持向量機[1-2]、神經網絡[3-4]等辨識模型，值得工程技術人員借鑒。

1 logistic回歸概率模型

設表征物質濃度的常用顏色有：藍色B、綠色G、紅色R、色調H、飽和度S，其讀數分別為x1、x2、x3和x4；對物質濃度進行類別劃分，類別值{1,2,…,J}（J為總類別數）；設研究對象（物體）記為X，其樣本集X={X1,X2,…,Xn}（Xi為樣本，i=1,2,…,n），且Xi=（xi1,xi2,xi3,xi4）。物質濃度類別Y∈{1,2,…,J}與其特征值（顏色讀數）之間存在非線性概率關系。設樣本Xi的濃度屬于第J類的概率為PJ，以Y=J作為參考類別，則對于Y=J（j=1,2,…,J-1），其logistic變換logit模型[5-6]為：

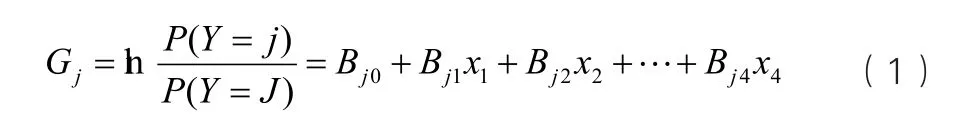
其中：Bj0,Bj1,…,Bj4為logistic回歸的偏回歸系數，表示變量xi對Y的影響大小，B0j為常數項；為樣本的第j個參數值；而對于參考類別, 其模型中的所有系數均為0，即GJ=0。由式（1）得：

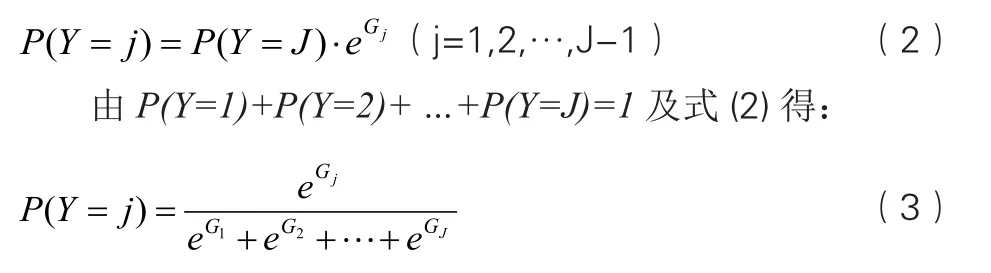
式（1）中的模型系數Bj0,Bj1,…,Bj4，由建模樣本數據及統計軟件SPSS19[7-8]完成。

2 數據來源及模型建立

2017年全國大學生數學建模C題給出一組二氧化硫的濃度與其顏色的讀數，見表1所示。

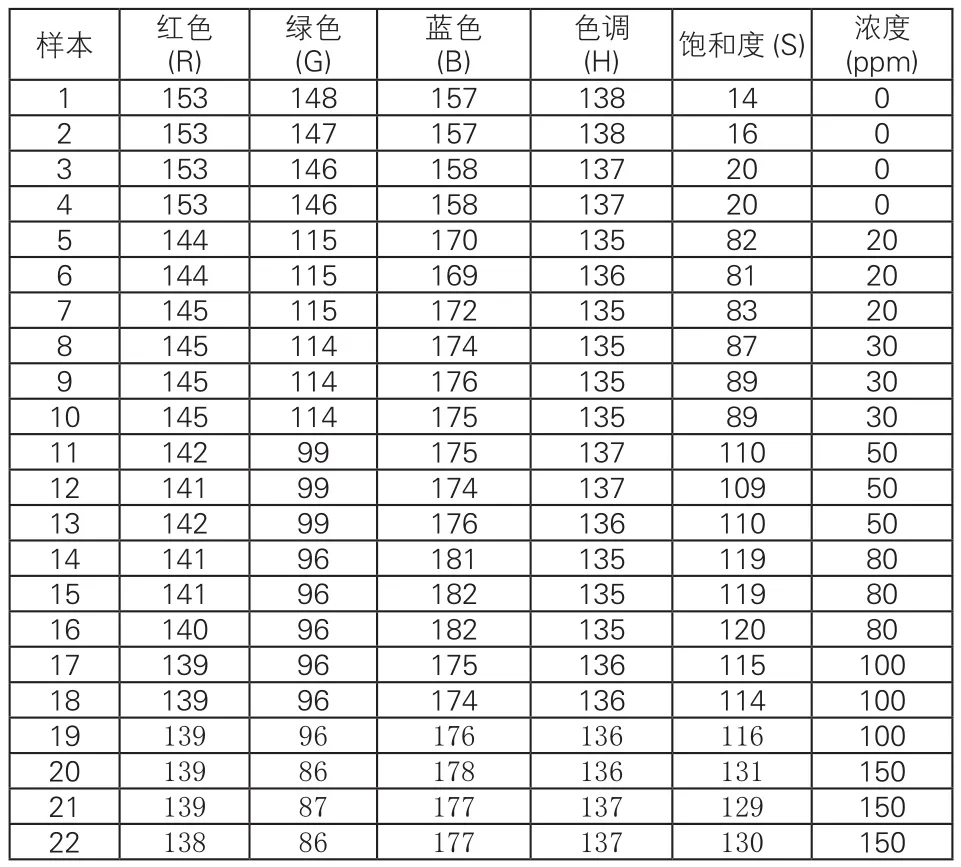
表1 二氧化硫的濃度與顏色讀數

首先按濃度大小分類，將濃度為0，20，30，50，80，100，150對應的樣本分別看成一類，共7類，類別值分別為1，2，3，4，5，6，7。當類別值為1時，則對應的濃度為0；當類別值為2時，則對應的濃度為20；當類別值3時，則對應的濃度為30；當類別值4時，則對應的濃度為50；依次類推。

將表1中二氧化硫指標數據及相應類別值列導入SPSS19中，選擇“分析”｜“回歸”｜“多項logistic”命令，按提示對話框完成所有操作，求得到的模型系數及模型見下式（4）～（10）：

由SPSS19得出模型擬合信息見表2，偽R方值見表3，擬合優度見表4。

表2 模型擬合信息

表3 三個偽決定系數R方

表4 擬合優度

從表2、表3及表4可知模型整體的顯著性非常高，因為p值遠小于0.05；從表3及表4可看出三個偽決定系數及擬合優度都很高，說明模型擬合效果非常好。下面給出模型的反向檢驗結果。

表5 歸類概率及判斷結果（精確到萬分位）

利用式（4）～（10）及式（3）可求出樣本隸屬各類的概率，并按最大概率原則歸類，計算結果見表5。

說明:從表5的判定結果知該模型的擬合預測精確為100%，表明logistic回歸為概率型非線性回歸模型具有很高的區分度，也說明將此類問題轉化成類別識別或模式識別問題來解決完全可行。另外，將該類問題看成決策問題用概率統計理論方法解答克服了傳統單一模型方法精確不高的缺點。

下面給同3個測試樣本（2017年全國大學生數學建模C題），見表6。

表6 測試樣本的二氧化硫的濃度與顏色讀數

將表6中3個樣本的特征指標值代入式（4）至式（10），并按式（3）求得樣本屬于各類的概率，并按最大概率歸類，如表7所示。

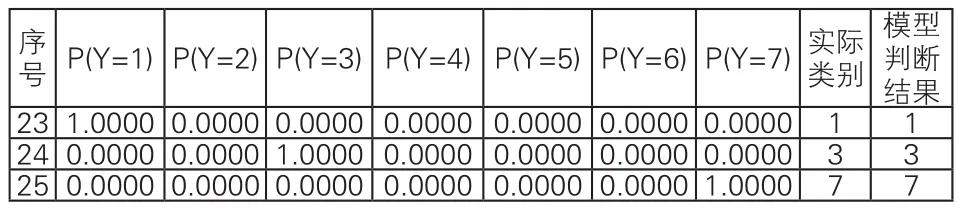
表7 測試樣本的濃度預測結果（精確到萬分位）

可見預測精度為100%，說明多項logistic概率回歸模型具有非常高的擬合預測能力，用物質濃度預測、以及其他模式識別或類別辨識完全可行。

3 結語

logistic回歸模型是一種基于概率的多元非線性問題的處理方法。實例分析表明該方法用于類別辨識或模式識別具有很高的精確度。對樣本物質濃度進行適當類別劃分，用表征濃度的特征數值創建多項 logistic回歸模型，并用統計軟件SPSS估算模型系數，通過對建模樣本和測試樣本的擬合預測精度的分析，準確度均達到100%，表明該模型預測效果很好，值得工程技術人員借鑒。