保密MIMO無線攜能系統的魯棒能效優化

楊廣宇，仇洪冰,2

(1. 西安電子科技大學 通信工程學院，陜西 西安 710071；2. 桂林電子科技大學 信息與通信學院，廣西 桂林 541004)

近年來，為確保無線攜能傳輸(Simultaneous Wireless Information and Power Transfer，SWIPT)系統中的通信安全，SWIPT與物理層保密傳輸相結合的研究日益引起學界和工業界的關注和研究．多輸入多輸出(Multiple Input Multiple Out，MIMO)或多輸入單輸出(Multiple Input Single Out，MISO)SWIPT系統中的研究主要集中于發射功率最小化和保密速率最大化問題[1-5]．文獻[5]研究了MISO SWIPT系統的保密速率最大化問題，提出了兩種優化方案，一種方案是用Charnes-Cooper變換將原非凸問題轉化為等效的半正定規劃，采用二分法和內點法聯合優化; 另一種是采用連續凸近似算法將原問題轉化為凸問題后，直接采用內點法最優化．

能量效率是未來綠色通信網絡的一項重要指標和基本要求．保密能量效率(Secrecy Energy Efficiency，SEE)定義為保密傳輸速率與總消耗功率之比，文獻[6]研究了三節點MIMO竊聽信道的保密能量效率最大化問題，采用Dinkelbach方法結合泰勒級數展開法求解問題的近似最優解．

在假定發送端掌握完全精準的信道狀態信息(Channel State Information，CSI)的情況下，文獻[7]研究了存在多個竊聽者的MIMO SWIPT系統的能效優化問題，由于目標函數包含凹函數之差以及多個變量之間的耦合，即便對目標函數參數化減式形式等效后，其仍是難以處理的非凸問題，經過等效變換，采用Dinkelbach方法和交替算法得到優化解．

在實際中，由于信道估計誤差和反饋延遲，獲得精準的CSI 是非常困難的．在CSI不精準的MIMO SWIPT系統中，文中提出一種魯棒的人工噪聲輔助優化方案．通過聯合設計波束成形矩陣、人工噪聲方差矩陣和功率分配(Power Splitting, PS)比，最大化系統最差情況的保密能量效率．目標函數是非線性分式規劃問題，且由于信道的不確定性，約束項中包含半無限約束項，這些因素導致原問題是非凸的，難以處理．通過S-Procedure和一階泰勒級數展開，把原問題近似等效為帶有線性矩陣不等式(Linear Matrix Inequality， LMI)約束的凸問題，針對等效后近似目標函數中相關優化變量的凸性特點，提出了一種基于Dinkelbach方法的兩級優化迭代算法．

1 系統模型和問題描述

考慮下行MIMO攜能系統．該系統包含一個配備NT個發射天線的發射端，一個配備NR個天線的信息和能量接收用戶，M個竊聽者，每個竊聽者配備NE個天線．發射端的基帶信號b=Ws+v，其中W是波束成形矩陣，s是攜帶保密信息的信號矢量，v～ CN(0，V)，是發射端產生的人工噪聲(Artificial Noise， AN)矢量．則用戶接收信號可表示為

(1)

第m個竊聽者接收到的信號可表示為

(2)

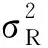
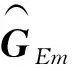
用戶配備有功率分配器用于對接收到的信號功率分流，一部分功率用于對解碼端接收到的信號解碼，一部分功率用于能量接收端對接收信號的能量收獲．分流到用戶解碼端的信號為

(3)

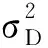
(4)

基于以上設定，系統最差情況下的保密傳輸速率[8]為

用戶能量收獲端收獲的功率為

(8)

其中，ζ表示能量轉換效率,ζ∈(0，1]．

系統消耗的總功率定義為

Ptot(W，V，ρ)=ξtr(WWH+V)+PC-EEH，

其中，ξ是功率放大器效率的倒數，ξ≥1；PC表示電路的恒定功率消耗．不失一般性，文中假定ζ=1，ξ=1．

在CSI非精準情況下，系統的最差情況保密能量效率定義為最差情況保密速率與所消耗總功率之比，即

ηEE(W，V，ρ)=RS(W，V，ρ)/Ptot(W，V，ρ) ．

(9)

則最差情況保密能量效率最大化問題可以描述為

其中，約束項式(10b)表示用戶能量接收端最小能量收獲約束，式(10c)表示最大發射功率約束．

求解優化問題式(10)的難點在于目標函數分式形式的非凸性，以及目標函數及約束項中優化變量間的耦合．

2 問題變換和算法

2.1 目標函數轉換

由于問題式(10)是典型的分式規劃問題，是難以處理的非凸問題．為此，引入參數化的減式函數[10-11]為

(11)

其中，λ≥0，Π是問題式(10)的可行域．

引理1 令λ*表示問題式(10)的最大SEE，優化問題式(10)和式(11)是等價的，當且僅當F(λ*)=0．

上述引理1給出了求解問題式(10)的方法，即采用兩級優化迭代算法求解最優(W，V，ρ)及對應的最大SEE．具體來講，在內層給定λ≥0，求解優化問題式(11); 外層利用Dinkelbach方法求方程F(λ)=0 的根，得到最優值λ*．

因此，首先研究λ給定情況下問題式(11)的優化．由于目標函數、最小能量收獲約束以及信道誤差，問題式(11)仍然是非凸問題．

2.2 內層問題的泰勒級數展開和LMI近似

在這節中，利用一階泰勒級數展開近似和LMI方法處理非凸問題式(11)．

固定λ的值不變，令Q=WWH，q=1/ρ，把式(6)和Ptot代入式(11)，整理后得到

(13)

式(12b)和式(12c)都是凸約束，但問題式(12)中目標函數的前兩項是關于(Q，V，q)的兩個凹函數之差，所以式(12)是非凸問題．對目標函數第2項進行線性化近似，在給定點(V(k)，q(k))對其進行一階泰勒級數展開，其中右上標k表示一階泰勒級數近似的第k次迭代．引入輔助變量t≥0，問題式(12)近似等效為

由式(13)Ptot(Q，V，q)的表達式可以看出，(Q，V)與q之間是相互耦合的，因此，式(14a)的目標函數不是關于(Q，V，q，t)的聯合凹函數，但若固定q，該目標函數是關于(Q，V，t)的凹函數，反之亦然．因此，可用分級算法最優化問題式(14)，可得

(15)

容易證明，問題式(16)優化求解后，其結果F(λ，q)是關于q的單變量凹函數，可用一維搜索算法黃金分割法求取F(λ)．因此，接下來將集中研究問題式(16)的優化．

問題式(16)的目標函數是關于(Q，V，t)的凹函數．但其約束項式(14c)不等式左邊是兩個凹函數之差[12]，是非凸不等式，所以問題式(16)仍然不是凸優化問題．引入輔助變量β1m≥0，β2m≥0，對式(14c)進行等效變換，即

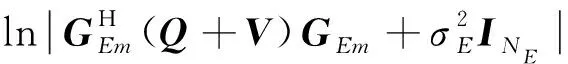
對于式(18)，由文獻[3]的引理2，可得如下關系：

(20)

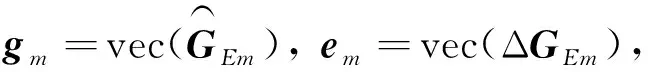
(21)

利用S-Procedure[13]和關系式tr(ABCD)=vec(AH)H(DT?B) vec(C)，式(20)和式(21)變換為等效的線性矩陣不等式，即

(22)

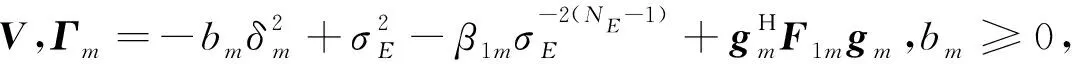
如前所述，兩個原因導致式(19)的非凸性，因此首先把不等式左邊項近似線性變換，將其在給定點(Q(k)，V(k))一階泰勒級數展開:

(23)

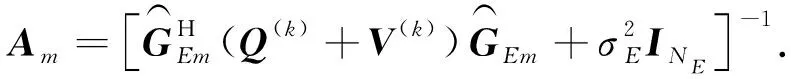
將式(23)代入式(19)整理后，得

(24)

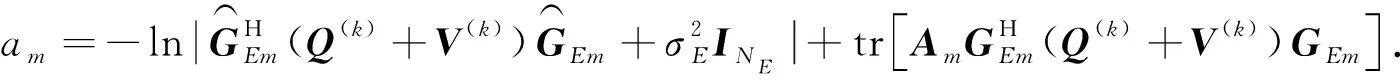
與式(20)的處理方法相同，式(24)等效變換為如下線性矩陣不等式：

(25)

經過上述變換后，在給定點(Q(k)，V(k)，q(k))，問題式(16)可近似等效為

其中，

問題式(26)是關于(Q，V，t，β1m，β2m，bm，cm)的聯合凸優化問題，可用內點法[14]求解．

2.3 基于Dinkelbach Method的迭代算法

基于以上分析，系統具體優化迭代算法如下:

初始化:i=1，λ1≥0，ε1，ε2，ε3，Q(0)，V(0)，q(0)．

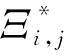
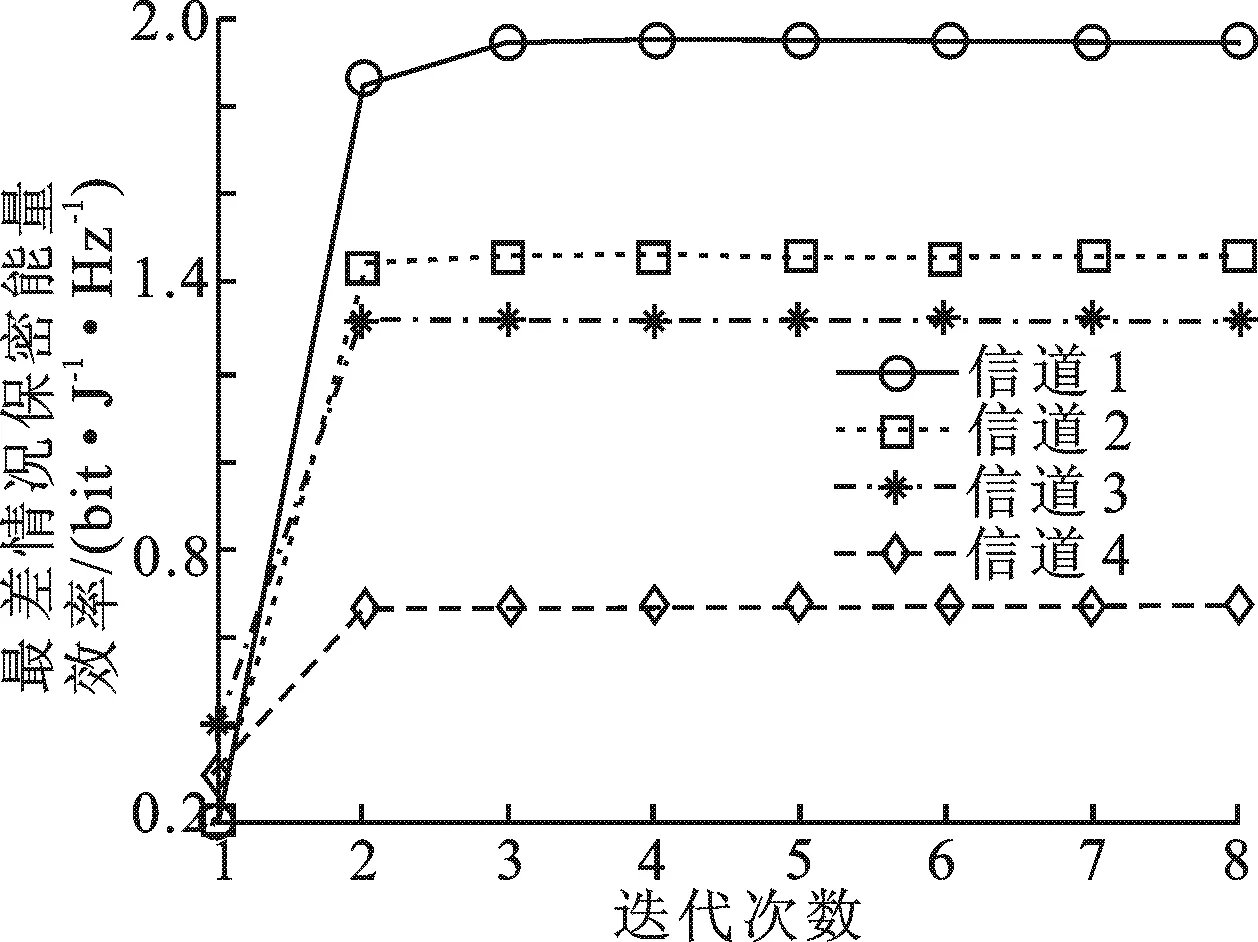
圖1 文中算法更新收斂速率

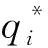
3 結果分析

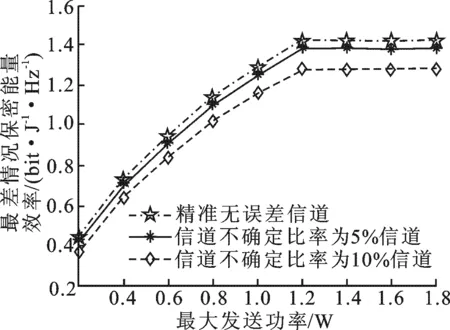
圖2 不同信道不確定性情況下最大發射功率對SEE的影響

從圖3中可看出，與無輔助人工噪聲(Artifical Noise，AN)優化方案相比，采用輔助噪聲方法可極大提高系統最差情況SEE．這是由于引入AN可以有效地“惡化”偷聽者對信息的接收．

圖3還表明，無論在低功率區還是在高功率區，固定功率分配因子ρ不變僅優化其他變量所獲得的SEE，總是低于或差于系統所有變量聯合優化得到的SEE．

圖3還顯示了所提方案和保密速率最大化(Secrecy Rate Maximization，SRM)方案相對于最大發射功率的性能．在低功率區，兩種方案的SEE都以相同的增長率增長，這說明在這一區域，最大功率傳輸是能量效率最大的．隨著發射功率進一步增加到較高功率區，文中方案的SEE保持穩定不變，而SRM方案的SEE是減小的．這是因為在SRM方案中，保密速率的增長率低于最大發射功率的增大率，從而導致能量效率降低．

圖4給出了所提算法與文獻[14]路徑跟蹤算法相對于最大發送功率的最差情況保密能量效率曲線．從圖4中可以看出，文中算法性能要優于路徑跟蹤算法的性能，其原因在于，文中算法對引入的輔助人工噪聲相關變量的優化，能夠以最小的功率消耗盡可能大的提高保密傳輸速率; 另外，路徑跟蹤算法的局部最優性也是其性能相對較差的原因．

4 結 束 語

針對MIMOME SWIPT系統，研究了在信道狀態信息不準確情況下系統的能量效率問題．通過減式等效、一階泰勒級數展開和S-Procedure變換，原問題變為易處理的對各變量的凸優化問題；針對最后形成的目標函數的特點，提出了一種兩級優化迭代算法．仿真結果和對比實驗，驗證了文中提出的人工噪聲輔助、波束成形、功率分配因子聯合優化方法，在信道存在誤差的場景下對系統提高最差情況SEE性能的有效性．