探究一題多解,培養發散思維——談初中數學發散思維的培養
江蘇省揚州市寶應縣廣洋湖鎮中心初級中學 馬亞允
創新發展是黨的十九大報告中傳遞出的重要信息,這是未來我國人才發展的一個趨勢,也為新時期的教育改革指明了方向。創造性思維是一個人和一個社會智力水平發展到一定高度的“產物”,也是產生更多具有社會意義成果的基石與來源。培養學生創造力和創造性思維成為新時期教育的首要任務,而發散思維則是測定學生是否具有創造力的重要標志,因此借助初中數學的學科優勢,著力培養中學生發散思維,值得每個數學教育者關注。筆者在實踐中發現,引導學生探究一題多解,對于發散思維的培養,思維靈活性激發以及創造性思維的形成具有積極的推動和促進作用。基于此,本文結合具體的教學案例,對此進行了深入研究和全面解析。
一、探究一題多解,發展發散思維
一個問題只能有一種解法的思維定式,導致了中學生思維僵化,很容易在題型稍加變化的情況下出現無解現象。數學是鍛煉學生思維多樣化的一門學科,通過探究一題多解,在讓學生了解到常規解法之后,引導他們再從不同角度對問題進行審視與,找到更多方法,并從中篩選出最優、最佳方案,是幫助他們提高解題效率,培養中學生聚合思維、發散思維等多種思維共同發展的有效途徑。以“多邊形內角和”一課為例。
師:三角形內角和為180度,這是我們都了解的,但是四邊形呢?大家知道嗎?
生1:應該是360度,我們學過的正方形和長方形,它們四個內角都是直角90度,所以內角和是360度。
師:不錯,但這兩種圖形在四邊形中是比較特殊的,不具有一般性。想想看怎樣將特殊問題轉化成一般問題?并由此推測出五邊形和六邊形的內角和。
這時可以鼓勵學生們通過小組合作的形式進行探究,并在討論之后以小組為代表進行發言。
小組1:四邊形可以先連接對角線,使一個四邊形變成兩個三角形,那么從三角形內角和就可以推導出四邊形的內角和。五邊形可以以一個點為頂點,向它對應的兩個角邊接,使一個五邊形轉化成三個三角形,那么五邊形內角和就是3個180度,即540度。
小組2:我們的方法相似,六邊形內角和就是先將它分成四個三角形的內角和相加,即720度。
師:不錯,大家都找到了一個簡單又有效的方法,那么從這個方法中是不是可以將多邊形(假設是個n邊形)內角和進行歸納?
小組3:通過觀察我們通過一個表格進行了歸納。

師:歸納得很到位,那么對于多邊形內角和的解法就沒有別的方法了嗎?
在教師的啟發引導下,學生們繼續更深層次的挖掘和討論。
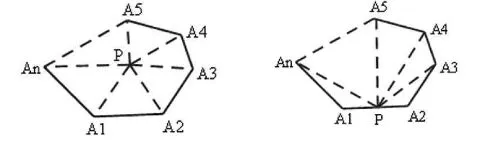
圖1
小組4:我們還想到了兩種方法,如圖1,一種是可以在n邊形里取任意點和所有頂點進行連接,就能夠得到“180°n-360°=180°(n-2)”。另一種就是在多邊形任意邊上取一點連接所有頂點,可以得到“180°(n-1)-180°=180°(n-2)”。
二、探究一題多用,碰撞思維火花
發散思維一方面是鍛煉學生思維靈活性,讓他們的思維不會停留在某個點或者某個面上,而是能夠跳出思維定式,多方位和多角度地對問題進行思考、分析和解決,在這個過程中完成思維的創造、創新和發展。另一方面是訓練學生思維深刻性,通過“一題多解”和“一題多用”將數學與現實連接起來,讓學生通過舉一反三,體驗數學在解決實際問題時的價值,從而提高對數學的認識。如在探究:“△ABC中,∠ABC的平分線與∠ACB的平分線相交于O點,∠A=40°,求∠BOC的度數是多少?”時,就可以通過一題多用對學生進行思維訓練:
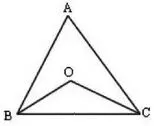
圖2
應用①:△ABC中,∠ABC的平分線與∠ACB的平分線相交于O點,∠A=a°,如圖2,那么∠BOC的度數是多少?它與∠A之間是否有數量關系存在?
應用②:△ABC中,∠ABC的平分線與∠ACB的平分線相交于O點,∠BOC=a°,那么∠A度數是多少?
應用③:△ABC中,∠BCE和∠CBD兩外角平分線相交于O點,∠A=a°,如圖3。那么∠BOC度數是多少?它與∠A之間是否有數量關系存在?
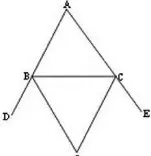
圖3

圖4
應用④:△ABC中,∠ACE外角平分線與∠ABC的角平分線相交于O點,∠A=a°,如圖4。那么∠BOC的度數是多少?它與∠A之間是否有數量關系存在?
結合中學生當前認知能力和水平以及數學思維的遞進性和層次性,秉承逐漸深入、逐步遞進和環環相扣的原則,設計多種題型進行“一題多用”,體現了數學思維的深刻性和嚴謹性,讓學生們由簡到難,由一般至特殊地對題目中隱藏的數學規律進行發現探究,對數學“建模思想”進行了滲透和強化。在這種訓練下,學生們的思維越來越靈活,也越來越深刻,完成了知識理論與實踐應用的融合和統一。
我國教育無可避免地受到傳統教育思想的影響,知識在老師手中一遍遍“填滿”學生腦海,而學生則通過不斷背誦復習讓其成為自己終身記憶,扎實的基礎知識反而束縛了學生的思維與思維,讓他們失去了創造與創新的機會。教育不應該是填滿學生的腦袋,而是要讓他們的思維“飛躍”。在初中數學教學中,“一題多解”的模式是對學生思維最好的訓練,但同時教育者也應該積極探索更好的方法,讓中學生在知識的同化與建構的過程中實現思維的提升與發展。

